表索引:数据库系统内部会使用多种不同的数据结构,用于内部元数据,核心数据结构,临时数据结构或表索引等目的。对于可能涉及范围扫描查询的表索引,哈希表可能不是最佳选择,因为它本质上是无序的。
表索引是表中列子集的副本,它存储了**[列的值,这一行在磁盘上的地址]**,它针对这些属性的子集进行了组织和/或排序,以便实现高效访问。因此,DBMS 无需执行全表扫描,而是可以通过在表索引上执行查找操作,更快速地找到特定元组。DBMS 确保表的内容与索引的内容在逻辑上始终保持同步。
在每个数据库创建索引的数量上存在一种权衡:
-
优点:更多的索引可以加快查询查找速度。
-
代价:索引会占用存储空间,并需要维护开销。
-
并发问题:在保持索引同步方面存在并发 (Concurrency) 考量。
DBMS的职责是找出执行查询时最适合使用的索引。
B+树:B+树是一种自平衡的树形数据结构,它保持数据有序,并允许在O(logn)的时间复杂度内进行搜索、顺序访问、插入和删除,它专门针对需要读写大块数据的面向磁盘的DBMS进行了优化。
几乎所有支持保序索引的现代 DBMS 都使用 B+ 树。虽然有一个特定的数据结构叫 B-Tree,但人们通常用这个术语泛指这一类数据结构。原始 B-Tree 和 B+ 树的主要区别在于:
-
B-Tree :在所有节点中存储键 (Key) 和值 (Value)。
-
B+ 树 :仅在叶子节点 (Leaf Nodes) 中存储值。
现代B+树的实现通常结合了其他B-Tree变体的特性,例如B-Link树中使用的兄弟指针。
形式化定义:形式上,B+树是一棵M路搜索树(M是一个节点可以拥有的最大子节点数),它具有以下属性:
-
完美平衡:即所有叶子节点都在相同的深度。
-
内部节点填充率:除根节点外,每个内部节点至少半满 (M/2-1<=键的数量<=M-1)
-
子节点关系:每个拥有 k 个键的内部节点,都有 k+1 个非空子节点。
节点结构:B+树中的每个节点都包含一个键/值对的数组。
叶子节点:叶子节点位于树的最底层,包含了实际的索引条目。
键源自索引所基于的列的属性,通常在节点内有序排列,支持范围查询。
叶子节点的"值"有两种存储方式:要么存储磁盘上实际数据行位置的指针,要么直接存储整行数据的内容。
内部节点:内部节点不存储任何实际数据,它们只负责指引搜索路径。
键作为路标,只是为了导航,不代表该键对应的数据一定存在。
值始终是指向子节点的指针。
空键:根据索引类型,空键将被聚集在第一个叶子节点或最后一个叶子节点。
插入操作:要向B+树插入新条目,必须向下遍历树,利用内部节点找出应将键插入哪个叶子节点。
1.查找:从根节点开始向下遍历,利用内部节点作为路标,找到目标键值应该所在的叶子节点L。
2.将新的键值对按顺序插入到L中。
3.检查:如果L已满,触发分裂。如果L未满,插入结束。
分裂的两种方式:
1.叶子节点分裂,创建新节点L2,将条目均匀分给L和L2。然后向上复制,选取中间键,将其复制一份插入到父节点中。因为叶子节点必须包含所有的数据键,中间键既要作为父节点的路标,也必须保留在叶子节点中作为实际数据存在。
2.内部节点分裂,当叶子节点导致父节点也满了,需要继续向上分裂。此时需要创建新内部节点,将条目均匀分配,选取中间键,将其完全移动到更上一层的父节点。
删除操作:在插入操作中,当树太满时我们需要分裂叶子,而在删除操作中,如果删除导致树不到半满,我们必须合并以重新平衡树。
1.查找:找到正确的叶子节点。
2.移除该条目,如果L至少半满,操作完成。否则,可以尝试从兄弟节点借一个条目,如果尝试失败,则将L与兄弟节点合并。
3.如果发生了合并,必须删除父节点中指向L的条目。
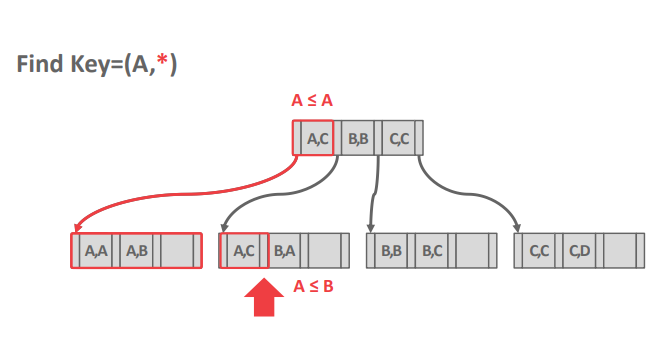
选择条件:由于 B+ 树是有序的,查找操作不仅拥有快速的遍历速度,而且不需要完整的键。如果查询提供了搜索键的任何前缀属性,DBMS就可以使用B+树索引,这与哈希索引不同,哈希索引要求搜索键的所有属性都必须存在,才能计算哈希值。
以下图为例,假设键为(列1,列2)这个整体,对于哈希函数,我们必须提供('A','C')才能计算出对应的哈希值,进而得到对应的值。而B+树的话,我们只需要像图中那样查找列1为'A'的键,然后找到第一个列1为'A'的键,然后顺序扫描叶子节点直到找到('A','C')。
重复键:在B+树中处理重复键(即多个元组拥有相同的索引键值)有两种方法:将ID作为键的一部分追加在后面,由于每个元组的ID都是唯一的,这能确保所有的键在B+树都是唯一可识别的。或允许叶子节点溢出到包含重复键的溢出节点中。
聚簇索引:聚簇索引是一种存储方式,不同于传统模式中索引和数据分离分为索引文件和数据文件的模式,聚簇索引模式下,数据库在磁盘上只有一个B+树文件结构,叶子存的键值对里面,值是元组而非元组地址。
由于B+树本身性质,所以天然符合聚簇索引。需要注意,在物理内存中,存储键值对以数组的方式存储,但在逻辑上仍然是一棵B+树,DBMS应该保存B+树根节点的地址,否则整棵树成为毫无意义的垃圾。类似的有二叉堆逻辑上为二叉树,但实际存储方式为数组。
因为数据在物理磁盘上只能有一种排列顺序,所以一张表只能有一个聚簇索引(通常是主键)。表中的数据按照主键指定的顺序进行存储,存储方式分为堆组织或索引组织。
隐式主键:由于某些DBMS总是使用聚簇索引,如果一张表没有显式定义主键,它们会自动创建一个隐式的行ID作为主键,而其他一些DBMS则可能完全无法使用聚簇索引。
堆聚簇:堆聚簇的数据库中,实现聚簇索引的方式与索引组织完全不同,它更像是一种维护操作,而非一种永久的存储结构。由于堆文件本身不强制顺序,DBMS想要实现聚簇,就必须执行一次物理重排。即使重排之后,一段时间后对文件又会趋于乱序。
聚簇最大的价值在于范围查询的性能:聚簇将逻辑上的有序转化为物理上的有序,从而极大减少磁盘I/O。如果没有聚簇,读100行连续的数据,可能需要产生100次随机I/O,有聚簇的话读100行连续的数据,可能只需要1次顺序I/O。
索引扫描页排序:由于直接从非聚簇索引检索元组效率较低(因为会导致随机I/O,即在不同页面之间跳转),DBMS可以采用一种优化策略:
1.先找出所有需要检索的元组。
2.根据它们的页面ID对这些请求进行排序。
3.按顺序获取数据。
B+树设计抉择:
节点大小:根据存储介质的不同,我们可能更倾向于使用更大或更小的节点:
根据存储介质的不同,我们可能更倾向于使用更大或更小的节点:
-
硬盘 (HDD):通常使用兆字节 (MB) 级别的节点。这样可以减少寻找数据所需的寻道次数,并将昂贵的磁盘读取开销摊薄到大块数据上。
-
内存数据库 (In-memory):可能使用小至 512 字节 的页大小。目的是为了让整个页能放入 CPU 缓存 中,并减少数据碎片。
-
工作负载影响:
-
点查询 (Point Queries):偏向尽可能小的页,以减少加载不必要的额外信息。
-
顺序扫描 (Sequential Scan):偏向大页,以减少读取次数。
-
合并阈值:虽然B+树规定删除操作后要合并欠载的节点,但有时暂时违反规则是有益的:
-
减少抖动:过于激进的合并可能导致抖动,即连续的删除和插入导致节点不断地分裂和合并。
-
批量合并:允许批量处理合并操作,减少昂贵的写锁占用树的时间。
-
延迟重建:有些策略(如 Postgres)允许树中存在较小的节点,稍后再统一重建,这会导致树暂时不平衡。
变长键:处理变长键有几种方法:
-
指针 (Pointers):存储指向键的指针。由于每次查找都要追踪指针(Pointer Chasing)效率极低,这种方法仅见于嵌入式设备。
-
变长节点 (Variable Length Nodes):允许节点本身大小不一。由于内存管理的开销巨大,这种方法基本不被使用。
-
填充 (Padding):将所有键对齐到最大长度。这会造成巨大的内存浪费,也很少见。
-
键映射/间接层 (Key Map/Indirection):这是几乎所有主流数据库采用的方法。注意是堆组织的数据库。
-
原理:在页内存储一个索引数组(字典),指向实际的键值对。此时索引文件只需要存储(键,(page_id,槽位号)),而索引数组存储(槽位号,offset)。
-
优点:显著节省空间。
-
前缀优化:在索引值旁存储每个键的前缀 (Prefix)。如果前缀已经不匹配,就不必追踪指针去查找完整键,从而大幅提升搜索和扫描速度。
-
节点内搜索:一旦我们到达某个节点,仍需在该节点内部进行搜索(要么是在内部节点中寻找下一个子节点,要么是在叶子节点中寻找目标键值)。虽然这听起来相对简单,但仍有一些权衡需要考虑:
线性搜索 (Linear):这是最简单的方案,即扫描节点中的每一个键直到找到目标。
-
优点:无需担心键的排序问题,使得插入和删除操作变得非常快。
-
缺点:相对低效,每次搜索的时间复杂度为 O(n)。
-
优化:可以使用 SIMD(单指令多数据流)或等效指令集进行向量化加速。
二分查找 (Binary):一种更高效的搜索方案是保持节点内键的有序性,并使用二分查找。
-
原理:跳转到节点的中间位置,根据键的比较结果向左或向右转。
-
优点:查找效率大幅提升,每次搜索的复杂度仅为 O(log n)。
-
缺点:插入操作变得更加昂贵,因为必须维护节点内键的排序。
优化技术
指针转换:由于B+树的每个节点都存储在缓冲池的页中,每次访问新节点时都需要从缓冲池获取,设计加锁和查找。为了完全跳过这一步,我们可以直接存储原始指针来代替页ID,从而完全避免缓冲池的查找开销。与其手动获取整棵树并放置指针,我们可以在正常遍历索引时,直接将页查找返回的指针存入父节点。我们必须跟踪哪些指针已经被转换,并且当它们指向的页被解除固定或被驱逐时,必须将指针转换为页ID。
批量插入:在最初构建B+树时,按常规方式插入每个键会导致频繁的分裂操作。由于叶子节点已经拥有兄弟指针,更高效的方式是先构建一个排好序的叶子节点链表,然后从下往上,利用每个节点的第一个键来构建索引层。根据具体情况,我们可以选择将叶子节点填得尽可能满以节省空间,或者保留一部分空间以减少未来分裂的频率。
前缀压缩:在同一个节点的键通常会有部分重叠的前缀(因为 B+ 树是有序的,相似的键会排在一起),与其在每个键中重复存储前缀,不如在节点开头存储一次前缀,然后在每个槽位中只包含该键特有的部分。
去重:在允许非唯一键的索引中,叶子节点可能会反复出现相同的键及其对应的不同值。优化方法是只写入一次键,后面跟着该键关联的所有值。
后缀截断:在大多数情况下,内部节点的键仅用作路标,而非实际键值。我们可以只存储最小必要前缀,只要它足以正确地将查询引导至正确的节点即可。这能节省内部节点的空间。
写优化B+树:节点的分裂和合并操作开销昂贵,某些B树变体会在内部节点中记录修改日志,并稍后延迟地将这些更新向下传播到叶子节点。