【算法设计与分析】递归与分治策略

hrrrrb2026-01-26 10:47

递归与分治策略

  • 递归与分治策略
    • 目录
    • [2.1 递归的概念](#2.1 递归的概念)
      • [2.1.1 什么是递归](#2.1.1 什么是递归)
      • [2.1.2 递归的执行过程](#2.1.2 递归的执行过程)
      • [2.1.3 递归与迭代](#2.1.3 递归与迭代)
      • [2.1.4 尾递归](#2.1.4 尾递归)
      • [2.1.5 Python 递归限制](#2.1.5 Python 递归限制)
    • [2.2 分治法的基本思想](#2.2 分治法的基本思想)
      • [2.2.1 分治法的三个步骤](#2.2.1 分治法的三个步骤)
      • [2.2.2 分治法的适用条件](#2.2.2 分治法的适用条件)
      • [2.2.3 递归树分析](#2.2.3 递归树分析)
      • [2.2.4 主定理](#2.2.4 主定理)
    • [2.3 二分搜索技术](#2.3 二分搜索技术)
      • [2.3.1 算法思想](#2.3.1 算法思想)
      • [2.3.2 迭代实现](#2.3.2 迭代实现)
      • [2.3.3 递归实现](#2.3.3 递归实现)
      • [2.3.4 二分搜索的变种](#2.3.4 二分搜索的变种)
    • [2.4 大整数的乘法](#2.4 大整数的乘法)
      • [2.4.1 问题分析](#2.4.1 问题分析)
      • [2.4.2 Karatsuba算法思想](#2.4.2 Karatsuba算法思想)
      • [2.4.3 Python实现](#2.4.3 Python实现)
      • [2.4.4 复杂度分析](#2.4.4 复杂度分析)
    • [2.5 Strassen 矩阵乘法](#2.5 Strassen 矩阵乘法)
      • [2.5.1 问题分析](#2.5.1 问题分析)
      • [2.5.2 传统矩阵乘法](#2.5.2 传统矩阵乘法)
      • [2.5.3 Strassen算法思想](#2.5.3 Strassen算法思想)
      • [2.5.4 Python实现](#2.5.4 Python实现)
      • [2.5.5 复杂度分析](#2.5.5 复杂度分析)
    • [2.6 棋盘覆盖](#2.6 棋盘覆盖)
      • [2.6.1 问题描述](#2.6.1 问题描述)
      • [2.6.2 分治策略](#2.6.2 分治策略)
      • [2.6.3 Python实现](#2.6.3 Python实现)
      • [2.6.4 复杂度分析](#2.6.4 复杂度分析)
    • [2.7 合并排序](#2.7 合并排序)
      • [2.7.1 算法思想](#2.7.1 算法思想)
      • [2.4.2 递归实现](#2.4.2 递归实现)
    • [2.8 快速排序](#2.8 快速排序)
      • [2.8.1 算法思想](#2.8.1 算法思想)
      • [2.8.2 标准实现](#2.8.2 标准实现)
      • [2.8.3 优化版本](#2.8.3 优化版本)
    • [2.9 线性时间选择](#2.9 线性时间选择)
      • [2.9.1 问题描述](#2.9.1 问题描述)
      • [2.9.2 随机选择算法](#2.9.2 随机选择算法)
      • [2.9.3 BFPRT算法（中位数的中位数）](#2.9.3 BFPRT算法（中位数的中位数）)
      • [2.9.4 复杂度分析](#2.9.4 复杂度分析)
    • [2.10 最接近点对问题](#2.10 最接近点对问题)
      • [2.10.1 问题描述](#2.10.1 问题描述)
      • [2.10.2 分治策略](#2.10.2 分治策略)
      • [2.10.3 关键优化：带状区域](#2.10.3 关键优化：带状区域)
      • [2.10.4 复杂度分析](#2.10.4 复杂度分析)
    • [2.11 循环赛日程表](#2.11 循环赛日程表)
      • [2.11.1 问题描述](#2.11.1 问题描述)
      • [2.11.2 分治策略](#2.11.2 分治策略)
      • [2.11.3 Python实现](#2.11.3 Python实现)
      • [2.11.4 复杂度分析](#2.11.4 复杂度分析)
    • 练习题
    • 答案
    • 本章小结

递归与分治策略

本章学习目标

  • 理解递归的概念和执行机制
  • 掌握分治法的基本思想和应用
  • 学习经典分治算法：二分搜索、合并排序、快速排序等
  • 理解递归树和主定理在复杂度分析中的应用

目录

  • [2.1 递归的概念](#2.1 递归的概念)
  • [2.2 分治法的基本思想](#2.2 分治法的基本思想)
  • [2.3 二分搜索技术](#2.3 二分搜索技术)
  • [2.4 大整数的乘法](#2.4 大整数的乘法)
  • [2.5 Strassen 矩阵乘法](#2.5 Strassen 矩阵乘法)
  • [2.6 棋盘覆盖](#2.6 棋盘覆盖)
  • [2.7 合并排序](#2.7 合并排序)
  • [2.8 快速排序](#2.8 快速排序)
  • [2.9 线性时间选择](#2.9 线性时间选择)
  • [2.10 最接近点对问题](#2.10 最接近点对问题)
  • [2.11 循环赛日程表](#2.11 循环赛日程表)
  • 练习题
  • 本章小结

2.1 递归的概念

2.1.1 什么是递归

递归定义：函数直接或间接调用自身的技术。

递归的三个要素：

  1. 基准情况（Base Case）：递归终止的条件
  2. 递归情况（Recursive Case）：问题规模缩小的步骤
  3. 收敛性：每次递归调用必须向基准情况靠近
python 复制代码 
def factorial(n: int) -> int:
    """
    阶乘的递归实现

    递归要素：
    - 基准情况：n <= 1 时返回 1
    - 递归情况：n * factorial(n-1)
    - 收敛性：n-1 向基准情况靠近
    """
    if n <= 1:           # 基准情况
        return 1
    return n * factorial(n - 1)  # 递归情况

2.1.2 递归的执行过程

递归调用使用调用栈（Call Stack）来管理：

python 复制代码 
def factorial_with_trace(n: int, depth: int = 0) -> int:
    """带跟踪输出的阶乘递归"""
    indent = "  " * depth
    print(f"{indent}factorial({n}) 被调用")

    if n <= 1:
        print(f"{indent}返回基准情况: 1")
        return 1

    result = n * factorial_with_trace(n - 1, depth + 1)
    print(f"{indent}返回: {result}")
    return result

# 执行 factorial_with_trace(3)
# 输出：
# factorial(3) 被调用
#   factorial(2) 被调用
#     factorial(1) 被调用
#     返回基准情况: 1
#   返回: 2
# 返回: 6

调用栈示意图：

复制代码 
调用 factorial(5)
├── factorial(4)  [栈帧1: n=5]
│   ├── factorial(3)  [栈帧2: n=4]
│   │   ├── factorial(2)  [栈帧3: n=3]
│   │   │   ├── factorial(1)  [栈帧4: n=2]
│   │   │   │   └── 返回 1  [栈帧5: n=1]
│   │   │   └── 返回 2*1=2
│   │   └── 返回 3*2=6
│   └── 返回 4*6=24
└── 返回 5*24=120

2.1.3 递归与迭代

python 复制代码 
# 递归版本
def sum_recursive(n: int) -> int:
    """递归求和：1 + 2 + ... + n"""
    if n <= 0:
        return 0
    return n + sum_recursive(n - 1)

# 迭代版本
def sum_iterative(n: int) -> int:
    """迭代求和：1 + 2 + ... + n"""
    total = 0
    for i in range(1, n + 1):
        total += i
    return total
特性 递归 迭代
代码简洁性 更简洁，直接反映数学定义 相对复杂
空间复杂度 O(n) 栈空间 O(1)
效率 有函数调用开销 更高效
适用场景 问题具有递归结构 注重性能

2.1.4 尾递归

尾递归：递归调用是函数的最后操作，可以优化为循环。

python 复制代码 
# 普通递归（不是尾递归）
def factorial_normal(n: int) -> int:
    if n <= 1:
        return 1
    return n * factorial_normal(n - 1)  # 递归后还有乘法操作

# 尾递归版本
def factorial_tail(n: int, accumulator: int = 1) -> int:
    """
    尾递归：递归调用是最后操作
    accumulator 保存中间结果
    """
    if n <= 1:
        return accumulator
    return factorial_tail(n - 1, n * accumulator)  # 纯尾递归

注意：Python 不支持尾递归优化，尾递归仍会消耗栈空间。

2.1.5 Python 递归限制

python 复制代码 
import sys

# 查看默认递归深度限制
print(f"默认递归深度限制: {sys.getrecursionlimit()}")  # 通常是 1000

# 修改递归深度限制（谨慎使用）
sys.setrecursionlimit(2000)

2.2 分治法的基本思想

2.2.1 分治法的三个步骤

分治法（Divide and Conquer）是一种算法设计范式：

  1. 分解（Divide）：将问题划分为若干个规模较小的子问题
  2. 解决（Conquer）：递归地解决各个子问题
  3. 合并（Combine）：将子问题的解合并成原问题的解
python 复制代码 
def divide_and_conquer(problem):
    """分治法通用模板"""
    # 基准情况：问题规模足够小，直接求解
    if is_base_case(problem):
        return solve_directly(problem)

    # 分解：将问题划分为子问题
    subproblems = divide(problem)

    # 解决：递归解决每个子问题
    solutions = [divide_and_conquer(sp) for sp in subproblems]

    # 合并：将子问题的解合并
    return combine(solutions)

2.2.2 分治法的适用条件

问题适合用分治法求解的条件：

  • 问题能分解为独立的子问题
  • 子问题与原问题性质相同
  • 子问题的解能合并为原问题的解
  • 存在基准情况

2.2.3 递归树分析

递归树是分析分治算法复杂度的直观方法。

归并排序的递归树：

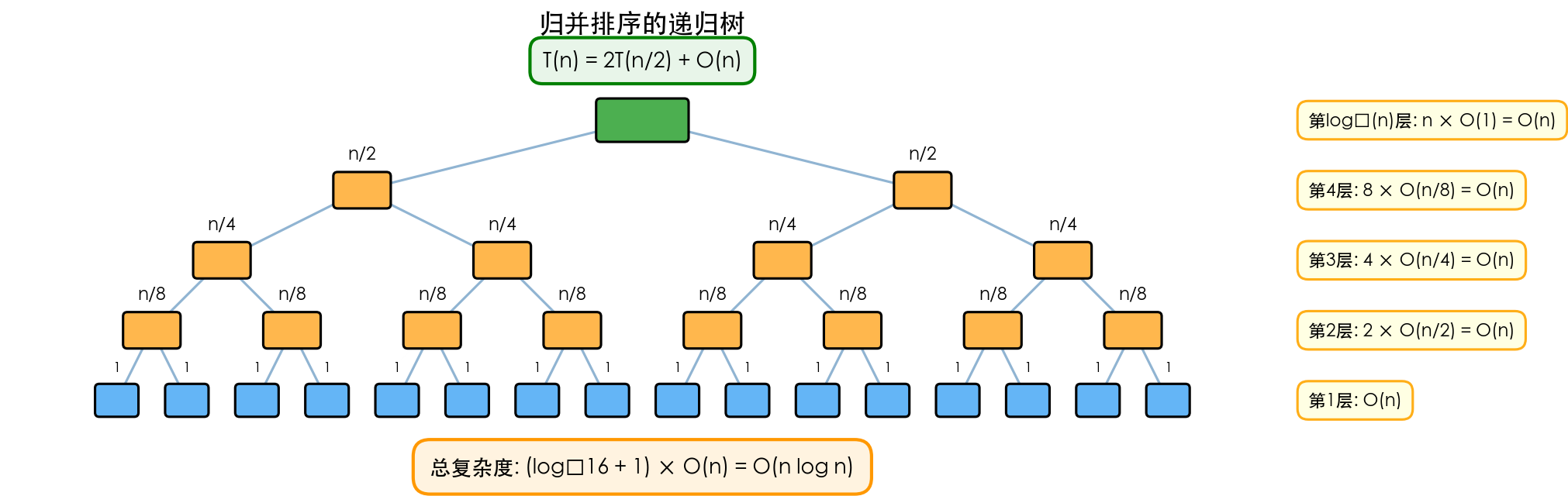
递归关系：T(n) = 2T(n/2) + O(n)

2.2.4 主定理

对于形如 T(n) = aT(n/b) + f(n) 的递归关系：

令 c = l o g b a c = log_ba c=logba ，比较 f(n) 与 n c n^c nc：

情况 条件 解
1 f ( n ) = O ( n ( c − ε ) ) ， ε > 0 f(n) = O(n^{(c-ε)})，ε > 0 f(n)=O(n(c−ε))，ε>0 T ( n ) = Θ ( n c ) T(n) = Θ(n^c) T(n)=Θ(nc)
2 f ( n ) = Θ ( n c × l o g k n ) f(n) = Θ(n^c × log^k n) f(n)=Θ(nc×logkn) T ( n ) = Θ ( n c × l o g ( k + 1 ) n ) T(n) = Θ(n^c × log^{(k+1)} n) T(n)=Θ(nc×log(k+1)n)
3 f ( n ) = Ω ( n ( c + ε ) ) ， ε > 0 f(n) = Ω(n^{(c+ε)})，ε > 0 f(n)=Ω(n(c+ε))，ε>0 T ( n ) = Θ ( f ( n ) ) T(n) = Θ(f(n)) T(n)=Θ(f(n))

2.3 二分搜索技术

2.3.1 算法思想

二分搜索（Binary Search）是分治法的经典应用：

前提条件：

  • 数组必须有序（升序或降序）
  • 支持随机访问

基本思想：每次比较中间元素，根据比较结果排除一半元素。

2.3.2 迭代实现

python 复制代码 
def binary_search(arr: list[int], target: int) -> int:
    """
    二分搜索 - 迭代版本

    时间复杂度: O(log n)
    空间复杂度: O(1)
    """
    left, right = 0, len(arr) - 1

    while left <= right:
        mid = left + (right - left) // 2  # 避免整数溢出

        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1

    return -1

2.3.3 递归实现

python 复制代码 
def binary_search_recursive(arr: list[int], target: int,
                             left: int, right: int) -> int:
    """
    二分搜索 - 递归版本

    时间复杂度: O(log n)
    空间复杂度: O(log n) - 递归栈
    """
    if left > right:
        return -1

    mid = left + (right - left) // 2

    if arr[mid] == target:
        return mid
    elif arr[mid] < target:
        return binary_search_recursive(arr, target, mid + 1, right)
    else:
        return binary_search_recursive(arr, target, left, mid - 1)

2.3.4 二分搜索的变种

python 复制代码 
def lower_bound(arr: list[int], target: int) -> int:
    """查找第一个 >= target 的位置"""
    left, right = 0, len(arr)
    while left < right:
        mid = left + (right - left) // 2
        if arr[mid] < target:
            left = mid + 1
        else:
            right = mid
    return left

def upper_bound(arr: list[int], target: int) -> int:
    """查找第一个 > target 的位置"""
    left, right = 0, len(arr)
    while left < right:
        mid = left + (right - left) // 2
        if arr[mid] <= target:
            left = mid + 1
        else:
            right = mid
    return left

2.4 大整数的乘法

2.4.1 问题分析

传统乘法：两个n位整数相乘，需要O(n²)次基本运算。

Karatsuba算法 ：通过分治策略将复杂度降低到 O ( n 1.585 ) O(n^{1.585}) O(n1.585)。

2.4.2 Karatsuba算法思想

将两个n位数x和y各分为两半：

复制代码 
x = a × 10^(n/2) + b
y = c × 10^(n/2) + d

其中 a、b、c、d 都是 n/2 位数

传统方法：x × y = ac × 10^n + (ad + bc) × 10^(n/2) + bd
需要4次乘法：ac、ad、bc、bd

Karatsuba的巧妙之处：只做3次乘法

复制代码 
z0 = b × d
z1 = (a + b) × (c + d)
z2 = a × c

x × y = z2 × 10^n + (z1 - z2 - z0) × 10^(n/2) + z0

2.4.3 Python实现

python 复制代码 
def karatsuba(x: int, y: int) -> int:
    """
    Karatsuba大整数乘法

    时间复杂度: O(n^1.585) ≈ O(n^log₂3)
    空间复杂度: O(n)
    """
    # 基准情况：小整数直接相乘
    if x < 10 or y < 10:
        return x * y

    # 计算位数
    n = max(len(str(x)), len(str(y)))
    m = n // 2

    # 分解：x = a×10^m + b, y = c×10^m + d
    high1, low1 = divmod(x, 10**m)
    high2, low2 = divmod(y, 10**m)

    # 3次递归乘法而非4次
    z0 = karatsuba(low1, low2)
    z1 = karatsuba((low1 + high1), (low2 + high2))
    z2 = karatsuba(high1, high2)

    # 合并结果
    return (z2 * 10**(2*m)) + ((z1 - z2 - z0) * 10**m) + z0


def traditional_multiply(x: int, y: int) -> int:
    """传统乘法（用于对比）"""
    return x * y  # Python内置也是优化的

2.4.4 复杂度分析

递归关系：T(n) = 3T(n/2) + O(n)

  • a = 3（3个子问题）
  • b = 2（每次分半）
  • f(n) = O(n)（加法、减法、移位）

应用主定理：

  • c = log₂3 ≈ 1.585
  • f ( n ) = n = O ( n ( 1.585 − ε ) ) ， ε = 0.585 > 0 f(n) = n = O(n^{(1.585-ε)})，ε = 0.585 > 0 f(n)=n=O(n(1.585−ε))，ε=0.585>0
  • 属于情况1

解 ： T ( n ) = Θ ( n l o g 2 3 ) ≈ Θ ( n 1.585 ) T(n) = Θ(n^{log₂3}) ≈ Θ(n^{1.585}) T(n)=Θ(nlog23)≈Θ(n1.585)

2.5 Strassen 矩阵乘法

2.5.1 问题分析

传统矩阵乘法：两个n×n矩阵相乘，需要O(n³)次标量乘法。

Strassen算法：通过分治策略将复杂度降低到O(n^2.81)。

2.5.2 传统矩阵乘法

对于两个n×n矩阵A和B：

复制代码 
C[i][j] = Σ(A[i][k] × B[k][j]), k = 0 to n-1

每个元素需要n次乘法和n-1次加法
共有n²个元素
时间复杂度: O(n³)

2.5.3 Strassen算法思想

将矩阵分为4个子块：

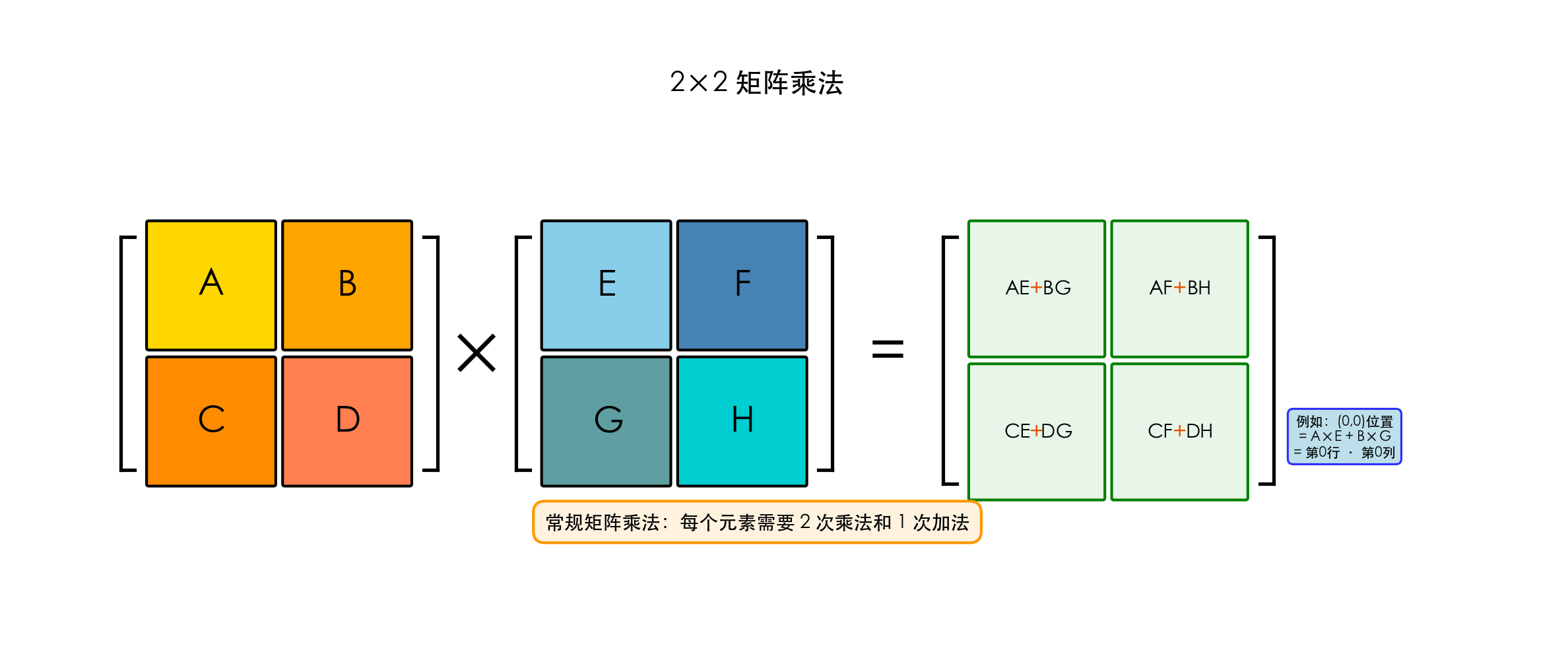
传统方法需要8次乘法：AE、AF、BG、BH、CE、CF、DG、DH

Strassen的巧妙之处：只用7次乘法

复制代码 
P1 = A × (F - H)
P2 = (A + B) × H
P3 = (C + D) × E
P4 = D × (G - E)
P5 = (A + D) × (E + H)
P6 = (B - D) × (G + H)
P7 = (A - C) × (E + F)

C11 = P5 + P4 - P2 + P6
C12 = P1 + P2
C21 = P3 + P4
C22 = P1 + P5 - P3 - P7

2.5.4 Python实现

python 复制代码 
def strassen(A: list[list[int]], B: list[list[int]]) -> list[list[int]]:
    """
    Strassen矩阵乘法

    时间复杂度: O(n^log₂7) ≈ O(n^2.81)
    空间复杂度: O(n²)
    """
    n = len(A)

    # 基准情况：小矩阵使用传统乘法
    if n <= 64:  # 阈值可调整
        return traditional_matrix_multiply(A, B)

    # 分块
    mid = n // 2
    A11, A12, A21, A22 = split_matrix(A, mid)
    B11, B12, B21, B22 = split_matrix(B, mid)

    # 7次递归乘法（而非8次）
    M1 = strassen(add_matrices(A11, A22), add_matrices(B11, B22))
    M2 = strassen(add_matrices(A21, A22), B11)
    M3 = strassen(A11, subtract_matrices(B12, B22))
    M4 = strassen(A22, subtract_matrices(B21, B11))
    M5 = strassen(add_matrices(A11, A12), B22)
    M6 = strassen(subtract_matrices(A21, A11), add_matrices(B11, B12))
    M7 = strassen(subtract_matrices(A12, A22), add_matrices(B21, B22))

    # 合并结果
    C11 = add_matrices(subtract_matrices(add_matrices(M1, M4), M5), M7)
    C12 = add_matrices(M3, M5)
    C21 = add_matrices(M2, M4)
    C22 = add_matrices(subtract_matrices(add_matrices(M1, M3), M2), M6)

    return combine_matrices(C11, C12, C21, C22, n)


def traditional_matrix_multiply(A: list[list[int]], B: list[list[int]]) -> list[list[int]]:
    """传统矩阵乘法 O(n³)"""
    n = len(A)
    C = [[0] * n for _ in range(n)]

    for i in range(n):
        for j in range(n):
            for k in range(n):
                C[i][j] += A[i][k] * B[k][j]
    return C


def split_matrix(M: list[list[int]], mid: int):
    """将矩阵分为4个子块"""
    return [
        [row[:mid] for row in M[:mid]],    # 左上
        [row[mid:] for row in M[:mid]],    # 右上
        [row[:mid] for row in M[mid:]],    # 左下
        [row[mid:] for row in M[mid:]]     # 右下
    ]


def combine_matrices(C11, C12, C21, C22, n):
    """合并4个子块为完整矩阵"""
    mid = n // 2
    C = [[0] * n for _ in range(n)]

    for i in range(mid):
        for j in range(mid):
            C[i][j] = C11[i][j]
            C[i][j + mid] = C12[i][j]
            C[i + mid][j] = C21[i][j]
            C[i + mid][j + mid] = C22[i][j]

    return C


def add_matrices(A, B):
    """矩阵加法"""
    n = len(A)
    return [[A[i][j] + B[i][j] for j in range(n)] for i in range(n)]


def subtract_matrices(A, B):
    """矩阵减法"""
    n = len(A)
    return [[A[i][j] - B[i][j] for j in range(n)] for i in range(n)]

2.5.5 复杂度分析

递归关系：T(n) = 7T(n/2) + O(n²)

  • a = 7（7个子问题）
  • b = 2（每次分半）
  • f(n) = O(n²)（矩阵加法、减法）

应用主定理：

  • c = log₂(7) ≈ 2.81
  • f ( n ) = n 2 = O ( n ( 2.81 − ε ) ) ， ε = 0.81 > 0 f(n) = n² = O(n^{(2.81-ε)})，ε = 0.81 > 0 f(n)=n2=O(n(2.81−ε))，ε=0.81>0
  • 属于情况1

解 ： T ( n ) = Θ ( n l o g 2 7 ) ≈ Θ ( n 2.81 ) T(n) = Θ(n^{log₂7}) ≈ Θ(n^{2.81}) T(n)=Θ(nlog27)≈Θ(n2.81)

注意事项：

  • Strassen算法的常数因子较大
  • 对于小矩阵（n < 100），传统方法可能更快
  • 实际应用中需要选择合适的阈值

2.6 棋盘覆盖

2.6.1 问题描述

棋盘覆盖问题 ：在一个 2 k × 2 k 2^k × 2^k 2k×2k的棋盘中，有一个特殊方格，用L型骨牌覆盖除特殊方格外的所有方格。

L型骨牌：由3个方格组成的骨牌，可以旋转和翻转。

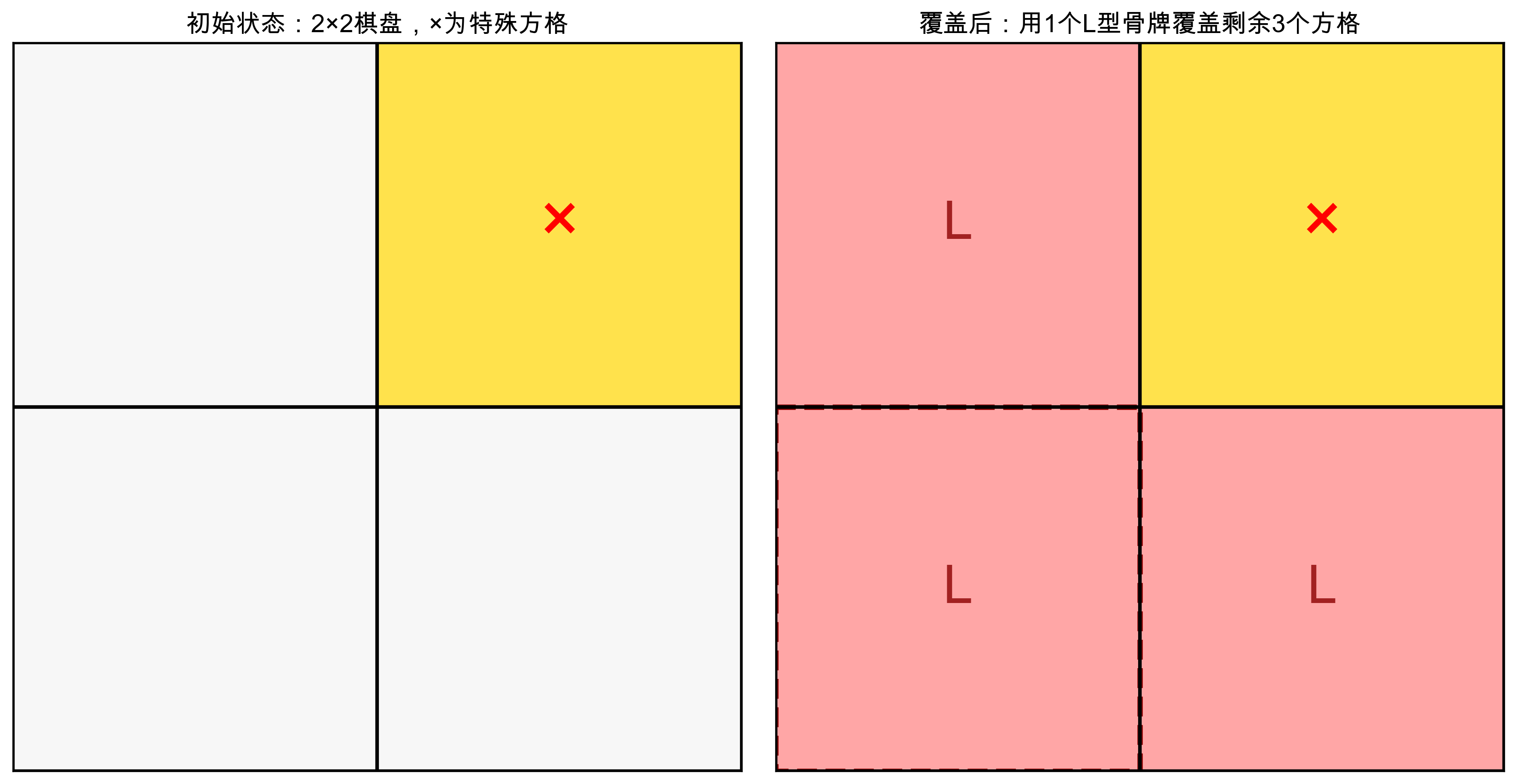
2.6.2 分治策略

基本思想 ：将 2 k × 2 k 棋盘分为 4 个 2 ( k − 1 ) × 2 ( k − 1 ) 2^k × 2^k棋盘分为4个2^{(k-1)} × 2^{(k-1)} 2k×2k棋盘分为4个2(k−1)×2(k−1)的子棋盘

  1. 分解：将棋盘分为4个子棋盘
  2. 定位：特殊方格必在其中一个子棋盘中
  3. 覆盖：在交汇处放置一个L型骨牌
  4. 递归：递归覆盖4个子棋盘

2.6.3 Python实现

python 复制代码 
def chessboard_cover(board: list[list[int]], tr: int, tc: int, dr: int, dc: int, size: int, tile: int):
    """
    棋盘覆盖问题

    Args:
        board: 棋盘，0表示未覆盖，正数表示骨牌编号
        tr, tc: 棋盘左上角行列号
        dr, dc: 特殊方格的行列号（相对于tr, tc）
        size: 棋盘大小（2的幂次）
        tile: 当前骨牌编号
    """
    if size == 1:
        return

    tile += 1  # 新的L型骨牌编号
    s = size // 2  # 子棋盘大小

    # 交汇处放置L型骨牌，覆盖3个子棋盘的各一个角
    # 左上子棋盘
    if dr < tr + s and dc < tc + s:
        chessboard_cover(board, tr, tc, dr, dc, s, tile)
    else:
        board[tr + s - 1][tc + s - 1] = tile
        chessboard_cover(board, tr, tc, tr + s - 1, tc + s - 1, s, tile)

    # 右上子棋盘
    if dr < tr + s and dc >= tc + s:
        chessboard_cover(board, tr, tc + s, dr, dc, s, tile)
    else:
        board[tr + s - 1][tc + s] = tile
        chessboard_cover(board, tr, tc + s, tr + s - 1, tc + s, s, tile)

    # 左下子棋盘
    if dr >= tr + s and dc < tc + s:
        chessboard_cover(board, tr + s, tc, dr, dc, s, tile)
    else:
        board[tr + s][tc + s - 1] = tile
        chessboard_cover(board, tr + s, tc, tr + s, tc + s - 1, s, tile)

    # 右下子棋盘（特殊方格在这里）
    if dr >= tr + s and dc >= tc + s:
        chessboard_cover(board, tr + s, tc + s, dr, dc, s, tile)
    else:
        board[tr + s][tc + s] = tile
        chessboard_cover(board, tr + s, tc + s, tr + s, tc + s, s, tile)


def create_chessboard(k: int, special_r: int, special_c: int) -> list[list[int]]:
    """
    创建k×k棋盘并覆盖

    Args:
        k: 棋盘大小参数（棋盘为2^k × 2^k）
        special_r, special_c: 特殊方格位置
    """
    size = 2 ** k
    board = [[0] * size for _ in range(size)]
    board[special_r][special_c] = -1  # 标记特殊方格

    chessboard_cover(board, 0, 0, special_r, special_c, size, 0)
    return board


def print_chessboard(board: list[list[int]]):
    """打印棋盘"""
    n = len(board)
    for i in range(n):
        for j in range(n):
            if board[i][j] == -1:
                print(" × ", end="")
            else:
                print(f"{board[i][j]:2} ", end="")
        print()

2.6.4 复杂度分析

时间复杂度：T(k) = 4T(k-1) + O(1)

设 n = 2^k，则 T(n) = 4T(n/2) + O(1)

  • a = 4, b = 2, c = log₂(4) = 2
  • f ( n ) = 1 = O ( n ( 2 − ε ) ) f(n) = 1 = O(n^{(2-ε)}) f(n)=1=O(n(2−ε))
  • 属于情况1

解 ： T ( n ) = Θ ( n 2 ) T(n) = Θ(n²) T(n)=Θ(n2)

骨牌数量 ： ( 4 k − 1 ) 3 ≈ n 2 3 {(4^k - 1) \over 3} ≈ {n² \over 3} 3(4k−1)≈3n2

2.7 合并排序

2.7.1 算法思想

合并排序（Merge Sort）是分治法的典型应用：

  1. 分解：将数组分为两半
  2. 解决：递归排序两半
  3. 合并：合并两个有序数组

2.4.2 递归实现

python 复制代码 
def merge_sort(arr: list[int]) -> list[int]:
    """
    合并排序 - 递归实现

    时间复杂度: O(n log n)
    空间复杂度: O(n) - 需要额外数组
    稳定性: 稳定排序
    """
    if len(arr) <= 1:
        return arr

    mid = len(arr) // 2
    left = merge_sort(arr[:mid])
    right = merge_sort(arr[mid:])

    return merge(left, right)


def merge(left: list[int], right: list[int]) -> list[int]:
    """合并两个有序数组"""
    result = []
    i = j = 0

    while i < len(left) and j < len(right):
        if left[i] <= right[j]:  # <= 保证稳定性
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1

    result.extend(left[i:])
    result.extend(right[j:])
    return result

2.8 快速排序

2.8.1 算法思想

快速排序（Quick Sort）采用分区策略：

  1. 选择基准（pivot）
  2. 分区：将小于pivot的放左边，大于的放右边
  3. 递归：排序左右两部分

2.8.2 标准实现

python 复制代码 
import random

def quick_sort(arr: list[int], low: int, high: int) -> None:
    """
    快速排序

    平均时间复杂度: O(n log n)
    最坏时间复杂度: O(n²)
    空间复杂度: O(log n)
    稳定性: 不稳定
    """
    if low < high:
        pivot_idx = partition(arr, low, high)
        quick_sort(arr, low, pivot_idx - 1)
        quick_sort(arr, pivot_idx + 1, high)


def partition(arr: list[int], low: int, high: int) -> int:
    """Lomuto 分区方案"""
    pivot = arr[high]
    i = low

    for j in range(low, high):
        if arr[j] < pivot:
            arr[i], arr[j] = arr[j], arr[i]
            i += 1

    arr[i], arr[high] = arr[high], arr[i]
    return i

2.8.3 优化版本

python 复制代码 
def quick_sort_optimized(arr: list[int], low: int, high: int) -> None:
    """优化的快速排序"""
    if low < high:
        # 小数组使用插入排序
        if high - low < 10:
            insertion_sort(arr, low, high)
            return

        # 三数取中法选择pivot
        pivot_idx = median_of_three(arr, low, high)
        arr[pivot_idx], arr[high] = arr[high], arr[pivot_idx]

        pivot_idx = partition(arr, low, high)

        # 尾递归优化
        if pivot_idx - low < high - pivot_idx:
            quick_sort_optimized(arr, low, pivot_idx - 1)
            quick_sort_optimized(arr, pivot_idx + 1, high)
        else:
            quick_sort_optimized(arr, pivot_idx + 1, high)
            quick_sort_optimized(arr, low, pivot_idx - 1)


def median_of_three(arr: list[int], low: int, high: int) -> int:
    """三数取中法"""
    mid = (low + high) // 2
    # 找中位数
    if arr[low] > arr[mid]:
        arr[low], arr[mid] = arr[mid], arr[low]
    if arr[low] > arr[high]:
        arr[low], arr[high] = arr[high], arr[low]
    if arr[mid] > arr[high]:
        arr[mid], arr[high] = arr[high], arr[mid]
    return mid


def insertion_sort(arr: list[int], low: int, high: int) -> None:
    """插入排序（用于小数组）"""
    for i in range(low + 1, high + 1):
        key = arr[i]
        j = i - 1
        while j >= low and arr[j] > key:
            arr[j + 1] = arr[j]
            j -= 1
        arr[j + 1] = key

2.9 线性时间选择

2.9.1 问题描述

选择问题（Selection Problem）：给定n个元素和整数k（1 ≤ k ≤ n），找出第k小的元素。

特殊情况：

  • k = 1：找最小元素
  • k = n：找最大元素
  • k = n/2：找中位数

2.9.2 随机选择算法

基于快速排序的分区思想，只递归进入包含第k元素的分区。

python 复制代码 
import random

def quick_select(arr: list[int], k: int) -> int:
    """
    随机选择算法 - 期望线性时间

    时间复杂度: 期望O(n)，最坏O(n²)
    空间复杂度: O(1) - 原地操作
    """
    if not arr:
        raise ValueError("数组不能为空")

    return quick_select_helper(arr, 0, len(arr) - 1, k - 1)


def quick_select_helper(arr: list[int], left: int, right: int, k: int) -> int:
    """在arr[left:right+1]中找第k小元素（k从0开始）"""
    if left == right:
        return arr[left]

    # 随机选择pivot
    pivot_idx = random.randint(left, right)
    pivot_idx = partition(arr, left, right, pivot_idx)

    if k == pivot_idx:
        return arr[k]
    elif k < pivot_idx:
        return quick_select_helper(arr, left, pivot_idx - 1, k)
    else:
        return quick_select_helper(arr, pivot_idx + 1, right, k)


def partition(arr: list[int], low: int, high: int, pivot_idx: int) -> int:
    """分区函数，返回pivot的最终位置"""
    pivot = arr[pivot_idx]
    arr[pivot_idx], arr[high] = arr[high], arr[pivot_idx]

    store_idx = low
    for i in range(low, high):
        if arr[i] < pivot:
            arr[store_idx], arr[i] = arr[i], arr[store_idx]
            store_idx += 1

    arr[store_idx], arr[high] = arr[high], arr[store_idx]
    return store_idx


def find_median(arr: list[int]) -> int:
    """找中位数"""
    n = len(arr)
    return quick_select(arr.copy(), (n + 1) // 2)


def find_kth_largest(arr: list[int], k: int) -> int:
    """找第k大元素"""
    n = len(arr)
    return quick_select(arr.copy(), n - k)

2.9.3 BFPRT算法（中位数的中位数）

BFPRT算法保证最坏情况下也是O(n)时间复杂度。

基本思想：

  1. 将n个元素分成⌈n/5⌉组，每组5个元素
  2. 找每组的中位数（排序）
  3. 递归找中位数的中位数作为pivot
  4. 分区后递归
python 复制代码 
def bfprt(arr: list[int], k: int) -> int:
    """
    BFPRT算法 - 最坏情况线性时间

    时间复杂度: O(n) - 最坏情况
    """
    if len(arr) <= 5:
        return sorted(arr)[k]

    # 分组并找中位数的中位数
    medians = [sorted(arr[i:i+5])[2] for i in range(0, len(arr), 5)]
    pivot = bfprt(medians, len(medians) // 2)

    # 三路分区
    less = [x for x in arr if x < pivot]
    equal = [x for x in arr if x == pivot]
    greater = [x for x in arr if x > pivot]

    if k < len(less):
        return bfprt(less, k)
    elif k < len(less) + len(equal):
        return pivot
    else:
        return bfprt(greater, k - len(less) - len(equal))

2.9.4 复杂度分析

随机选择算法：

  • 平均情况：T(n) = T(n/2) + O(n) = O(n)
  • 最坏情况：T(n) = T(n-1) + O(n) = O(n²)（每次都选到最大或最小）

BFPRT算法：

  • 递归关系：T(n) = T(n/5) + T(7n/10) + O(n)
  • 关键：至少3/10的元素被排除
  • 最坏情况：T(n) = O(n)

2.10 最接近点对问题

2.10.1 问题描述

最接近点对问题：给定平面上n个点，找出距离最近的两个点。

暴力法：枚举所有点对，O(n²)时间。

分治法目标：O(n log n)时间。

2.10.2 分治策略

基本思想：

  1. 按x坐标排序
  2. 分治：将点集分为左右两半
  3. 递归：分别找出左右两半的最近点对
  4. 合并：处理跨中线的点对

关键：带状区域内每点最多只需检查6个点。

python 复制代码 
import math
from typing import List, Tuple

Point = Tuple[float, float]


def closest_pair(points: List[Point]) -> Tuple[float, Point, Point]:
    """
    最接近点对问题 - 分治法

    时间复杂度: O(n log n)
    空间复杂度: O(n)
    """
    # 按x坐标排序
    points_sorted = sorted(points, key=lambda p: p[0])

    return closest_pair_helper(points_sorted)


def closest_pair_helper(points: List[Point]) -> Tuple[float, Point, Point]:
    """递归 helper函数"""
    n = len(points)

    # 基准情况
    if n <= 3:
        return brute_force_closest(points)

    mid = n // 2
    mid_point = points[mid]

    # 递归找左右两半的最近点对
    left_points = points[:mid]
    right_points = points[mid:]

    dl, pl1, pl2 = closest_pair_helper(left_points)
    dr, pr1, pr2 = closest_pair_helper(right_points)

    d = min(dl, dr)
    (d_min, p1, p2) = (dl, pl1, pl2) if dl < dr else (dr, pr1, pr2)

    # 处理跨中线的点对
    strip = []
    for p in points:
        if abs(p[0] - mid_point[0]) < d:
            strip.append(p)

    # strip内按y坐标排序
    strip.sort(key=lambda p: p[1])

    # 检查strip内的点对
    for i in range(len(strip)):
        for j in range(i + 1, len(strip)):
            if strip[j][1] - strip[i][1] >= d:
                break
            dist = distance(strip[i], strip[j])
            if dist < d_min:
                d_min = dist
                p1, p2 = strip[i], strip[j]

    return d_min, p1, p2


def brute_force_closest(points: List[Point]) -> Tuple[float, Point, Point]:
    """暴力法找最近点对"""
    min_dist = float('inf')
    p1 = p2 = None

    for i in range(len(points)):
        for j in range(i + 1, len(points)):
            dist = distance(points[i], points[j])
            if dist < min_dist:
                min_dist = dist
                p1, p2 = points[i], points[j]

    return min_dist, p1, p2


def distance(p1: Point, p2: Point) -> float:
    """计算两点间距离"""
    return math.sqrt((p1[0] - p2[0])**2 + (p1[1] - p2[1])**2)

2.10.3 关键优化：带状区域

重要性质：对于带状区域内的点，每个点最多只需要检查后面6个点。

原因：

  • 带状区域宽度为d
  • 在d×2d矩形内，最多只能有6个点两两距离≥d
  • 否则会违反递归假设

2.10.4 复杂度分析

递归关系：T(n) = 2T(n/2) + O(n log n)

  • 排序：O(n log n)
  • 递归：2T(n/2)
  • 带状区域：O(n)（每个点最多检查6个）

使用主定理的推广：T(n) = O(n log²n)

实际实现中，带状区域的排序可以优化到O(n)，总复杂度为O(n log n)。

2.11 循环赛日程表

2.11.1 问题描述

循环赛日程表问题 ：有n个选手进行循环赛， n = 2 k n = 2^k n=2k，要求：

  • 每个选手必须与其他n-1个选手各比赛一次
  • 每个选手每天只能比赛一次
  • 循环赛在n-1天内结束

2.11.2 分治策略

基本思想：将问题分为规模减半的子问题

复制代码 
k=1 (2个选手):          k=2 (4个选手):
  1 2                     1 2 3 4
  2 1                     2 1 4 3
                          3 4 1 2
                          4 3 2 1

分治构造方法：

  1. 将n个选手分为两半：前n/2个和后n/2个
  2. 递归构造两个子问题的日程表
  3. 合并：在左上角填前半部分日程，右下角填后半部分日程
  4. 右上角和左下角通过交换得到

2.11.3 Python实现

python 复制代码 
def round_robin_schedule(k: int) -> list[list[int]]:
    """
    循环赛日程表 - 分治法

    Args:
        k: 规模参数，n = 2^k

    Returns:
        n×n的日程表，schedule[i][j]表示第i个选手在第j天的对手
    """
    n = 2 ** k
    schedule = [[0] * n for _ in range(n)]

    # 基准情况：k=1，只有2个选手
    if k == 1:
        schedule[0][0] = 2
        schedule[0][1] = 1
        schedule[1][0] = 1
        schedule[1][1] = 2
        return schedule

    # 分治：构造左上角
    half_size = 2 ** (k - 1)
    sub_schedule = round_robin_schedule(k - 1)

    # 复制到左上角和右下角
    for i in range(half_size):
        for j in range(half_size):
            schedule[i][j] = sub_schedule[i][j]
            schedule[i + half_size][j + half_size] = sub_schedule[i][j]

    # 右上角和左下角
    for i in range(half_size):
        for j in range(half_size):
            schedule[i][j + half_size] = sub_schedule[i][j] + half_size
            schedule[i + half_size][j] = sub_schedule[i][j] + half_size

    return schedule


def print_schedule(schedule: list[list[int]]) -> None:
    """打印日程表"""
    n = len(schedule)
    print(f"{'选手':<6}", end="")
    for day in range(n - 1):
        print(f"第{day+1}天", end="  ")
    print()

    for i in range(n):
        print(f"选手{i+1:<3}", end="  ")
        for j in range(n - 1):
            print(f"{schedule[i][j]:3}", end="  ")
        print()


# 示例：8个选手的循环赛日程表
if __name__ == "__main__":
    k = 3  # 8个选手
    schedule = round_robin_schedule(k)
    print_schedule(schedule)

    # 输出：
    # 选手    第1天  第2天  第3天  第4天  第5天  第6天  第7天
    # 选手1    2    3    4    5    6    7    8
    # 选手2    1    4    3    6    5    8    7
    # 选手3    4    1    2    7    8    5    6
    # 选手4    3    2    1    8    7    6    5
    # 选手5    6    7    8    1    2    4    3
    # 选手6    5    8    7    2    1    3    4
    # 选手7    8    5    6    3    4    1    2
    # 选手8    7    6    5    4    3    2    1

2.11.4 复杂度分析

时间复杂度：T(k) = 2T(k-1) + O(n²)

  • 递归：2T(k-1)
  • 合并：O(n²)（填充日程表）

设 n = 2^k，则 T(n) = 2T(n/2) + O(n²) = O(n² log n)

空间复杂度：O(n²) - 需要n×n的日程表

练习题

概念题

  1. 递归的三个要素是什么？

  2. 分治法的三个步骤是什么？

  3. 二分搜索的前提条件是什么？

  4. 比较合并排序和快速排序：

    • 时间复杂度（最坏、平均）
    • 空间复杂度
    • 稳定性

  5. 使用主定理分析 T(n) = 4T(n/2) + n 的复杂度

  6. Karatsuba算法为什么能提高大整数乘法的效率？

  7. Strassen矩阵乘法的核心创新是什么？

  8. 棋盘覆盖问题中，每次递归如何处理四个子棋盘？

  9. 快速选择算法相比完整排序的优势在哪里？

  10. 最接近点对问题中，为什么带状区域每个点最多检查6个点？

代码分析题

  1. 分析以下递归函数的时间复杂度：

    python 复制代码 
    def func(n):
    if n <= 1:
        return 1
    return func(n/3) + func(n/3) + func(n/3) + n

  2. 以下函数是否存在问题？如果存在，如何修正？

    python 复制代码 
    def binary_search(arr, target):
    left, right = 0, len(arr)
    while left < right:
        mid = (left + right) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            left = mid
        else:
            right = mid
    return -1

编程题

  1. 实现pow(x, n)函数，计算x的n次幂，要求O(log n)时间复杂度。

  2. 实现搜索旋转排序数组。

  3. 实现查找数组中第k大的元素，要求平均O(n)时间复杂度。

  4. 实现汉诺塔问题（经典递归问题）。

  5. 实现全排列生成（使用递归回溯）。

  6. 给定二维平面上的n个点，实现最近点对算法。

综合题

  1. 设计一个算法，在O(n)时间内判断数组中是否存在重复元素。

  2. 分析并比较以下排序算法的适用场景：

    • 归并排序
    • 快速排序
    • 堆排序（提示：第4章会学习）

答案

概念题答案

  1. 递归三要素：基准情况、递归情况、收敛性

  2. 分治三步骤：分解、解决、合并

  3. 二分搜索前提：数组有序、支持随机访问

  4. 合并排序 vs 快速排序：

    • 归并排序最坏O(n log n)，空间O(n)，稳定
    • 快速排序最坏O(n²)，空间O(log n)，不稳定

  5. 主定理：a=4, b=2, c=2, f(n)=n=O(n²)，情况1，T(n)=Θ(n²)

  6. Karatsuba算法：将n位数分为两个n/2位数后，通过巧妙的代数变换，只需要3次乘法而非4次，将时间复杂度从O(n²)降至O(n^1.585)

  7. Strassen核心创新：将矩阵分块后，通过7个特殊的乘法组合代替8次常规乘法，将时间复杂度从O(n³)降至O(n^2.81)

  8. 棋盘覆盖处理：每次递归时，特殊方格所在的子棋盘直接递归处理；其他三个子棋盘在交汇处用一块L型骨牌覆盖，创建新的特殊方格后递归

  9. 快速选择优势：只递归进入包含第k元素的分区，期望O(n)时间，而排序需要O(n log n)

  10. 带状区域优化：在min_dist×min_dist的矩形内，根据鸽巢原理最多只能有6个点（每个点占据一个1/6圆区域）

代码分析题答案

  1. T(n) = 3T(n/3) + n，a=3, b=3, c=1，f(n)=Θ(n^1)，情况2，T(n)=Θ(n log n)

  2. 问题：

    • right初始应为len(arr) - 1
    • 更新left = mid会导致死循环，应为left = mid + 1
    • 更新right = mid会导致死循环，应为right = mid - 1

编程题答案

  1. 快速幂：

    python 复制代码 
    def pow(x: float, n: int) -> float:
    if n == 0:
        return 1.0
    if n < 0:
        return 1.0 / pow(x, -n)
    half = pow(x, n // 2)
    if n % 2 == 0:
        return half * half
    else:
        return half * half * x

  2. 搜索旋转数组：

    python 复制代码 
    def search_rotated(nums: list[int], target: int) -> int:
    left, right = 0, len(nums) - 1
    while left <= right:
        mid = (left + right) // 2
        if nums[mid] == target:
            return mid
        if nums[left] <= nums[mid]:
            if nums[left] <= target < nums[mid]:
                right = mid - 1
            else:
                left = mid + 1
        else:
            if nums[mid] < target <= nums[right]:
                left = mid + 1
            else:
                right = mid - 1
    return -1

  3. 查找第k大元素（使用快速选择）：

    python 复制代码 
    import random

def find_kth_largest(nums: list[int], k: int) -> int:
    """查找第k大元素，k从1开始"""
    # 转换为查找第(len(nums)-k+1)小元素
    return quick_select(nums, len(nums) - k + 1)

def quick_select(nums: list[int], k: int) -> int:
    if len(nums) == 1:
        return nums[0]

    pivot = random.choice(nums)
    lows = [x for x in nums if x < pivot]
    highs = [x for x in nums if x > pivot]
    pivots = [x for x in nums if x == pivot]

    if k <= len(lows):
        return quick_select(lows, k)
    elif k > len(lows) + len(pivots):
        return quick_select(highs, k - len(lows) - len(pivots))
    else:
        return pivots[0]

  4. 汉诺塔问题：

    python 复制代码 
    def hanoi(n: int, source: str, target: str, auxiliary: str) -> None:
    """
    将n个盘子从source柱子移动到target柱子

    参数：
        n: 盘子数量
        source: 源柱子
        target: 目标柱子
        auxiliary: 辅助柱子
    """
    if n == 1:
        print(f"移动盘子1从{source}到{target}")
        return

    # 将n-1个盘子从source移动到auxiliary
    hanoi(n - 1, source, auxiliary, target)

    # 将第n个盘子从source移动到target
    print(f"移动盘子{n}从{source}到{target}")

    # 将n-1个盘子从auxiliary移动到target
    hanoi(n - 1, auxiliary, target, source)

  5. 全排列生成：

    python 复制代码 
    def permute(nums: list[int]) -> list[list[int]]:
    """生成数组的所有全排列"""
    result = []
    backtrack(nums, [], result)
    return result

def backtrack(nums: list[int], path: list[int],
              result: list[list[int]]) -> None:
    if not nums:
        result.append(path[:])
        return

    for i in range(len(nums)):
        # 选择当前元素
        path.append(nums[i])
        # 递归处理剩余元素
        backtrack(nums[:i] + nums[i+1:], path, result)
        # 撤销选择
        path.pop()

  6. 最近点对算法 ：参见 scripts/chapter2/advanced_divide_conquer.py 中的完整实现

综合题答案

  1. 判断重复元素：

    python 复制代码 
    def contains_duplicate(nums: list[int]) -> bool:
    """判断数组中是否存在重复元素"""
    seen = set()
    for num in nums:
        if num in seen:
            return True
        seen.add(num)
    return False

# 如果要求O(1)额外空间（不修改原数组），可以先排序
def contains_duplicate_sort(nums: list[int]) -> bool:
    nums_sorted = sorted(nums)
    for i in range(1, len(nums_sorted)):
        if nums_sorted[i] == nums_sorted[i - 1]:
            return True
    return False

  2. 排序算法适用场景：

    算法 时间复杂度 空间复杂度 稳定性 适用场景
    归并排序 O(n log n) O(n) 稳定 外部排序、稳定排序需求
    快速排序 O(n log n)平均 O(log n) 不稳定 通用排序、内存排序
    堆排序 O(n log n) O(1) 不稳定 内存受限、找前k大

    选择建议：

    • 追求性能且不在乎稳定：快速排序
    • 需要稳定排序：归并排序
    • 内存受限：堆排序
    • 数据量小：插入排序（简单高效）

本章小结

核心知识点

  1. 递归：三个要素、调用栈、与迭代的权衡
  2. 分治法：分解-解决-合并、递归树分析、主定理
  3. 经典算法：二分搜索O(log n)、合并排序O(n log n)、快速排序O(n log n)平均

与后续章节关联

本章内容 后续章节
递归基础 所有章节
分治思想 动态规划、贪心算法对比
合并排序 外部排序
快速排序 选择问题

下一章预告：动态规划将学习通过保存子问题解避免重复计算。

相关推荐
客卿1232 小时前
力扣二叉树简单题整理--（包含常用语法的讲解）
算法·leetcode·职场和发展
We་ct2 小时前
LeetCode 28. 找出字符串中第一个匹配项的下标：两种实现与深度解析
前端·算法·leetcode·typescript
血小板要健康2 小时前
118. 杨辉三角，力扣
算法·leetcode·职场和发展
_OP_CHEN2 小时前
【算法基础篇】（五十一）组合数学入门：核心概念 + 4 种求组合数方法，带你快速熟悉组合问题！
c++·算法·蓝桥杯·排列组合·组合数学·组合数·acm/icpc
漫随流水2 小时前
leetcode回溯算法（491.非递减子序列）
数据结构·算法·leetcode·回溯算法
睡一觉就好了。2 小时前
排序--直接排序，希尔排序
数据结构·算法·排序算法
_pinnacle_2 小时前
多维回报与多维价值矢量化预测的PPO算法
神经网络·算法·强化学习·ppo·多维价值预测
Yzzz-F2 小时前
P3842 [TJOI2007] 线段
算法
YuTaoShao2 小时前
【LeetCode 每日一题】1984. 学生分数的最小差值
算法·leetcode·排序算法
热门推荐
01GitHub 镜像站点02OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)03Claude Code Skills 实用使用手册04UV安装并设置国内源05Open Code教程（四）| 高级配置与集成06Linux下V2Ray安装配置指南07在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）08安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）09MC.JS 网页版《我的世界》 免安装中文版10BongoCat - 跨平台键盘猫动画工具