
摘要
量子近似优化算法(QAOA)是一种重要的量子算法,旨在为经典计算机难以应对的组合优化问题寻找近似解。在当前量子硬件受噪声限制且量子比特数量有限的时代,模拟 QAOA 对于研究仍然至关重要。然而,现有最先进的模拟框架存在执行时间长、功能不够全面、可用性和通用性不足的问题,通常需要用户自行实现关键功能。此外,这些框架主要限于Python语言,限制了它们在更安全、更快速的语言(如Rust)中的应用,而后者具备高级并行化能力等优势。本文中,我们利用NVIDIA CUDA工具包开发了一个GPU加速的QAOA模拟框架。该框架提供了完整的QAOA模拟接口,支持计算(精确)期望值、直接访问状态向量、快速采样以及使用先进的最先进梯度计算技术的高性能优化方法。该框架设计用于Python和Rust,为集成到各种应用中提供了灵活性,包括那些需要在其核心利用QAOA实现快速算法的应用。我们在MaxCut问题上对新框架的性能进行了严格的基准测试,并与当前最先进的通用量子电路模拟框架Qiskit和Pennylane以及专门的QAOA模拟工具QOKit进行了比较。评估结果表明,我们的方法在运行时间上优于现有最先进的解决方案,提升可达多个数量级。我们的实现已在https://github.com/JFLXB/cuaoa和Zenodo [1]上公开发布。
**关键词:**量子计算,量子优化,QAOA,量子电路模拟,CUDA,高性能计算
I 引言
在优化问题领域,量子优势最具前景的方法之一是量子近似优化算法(QAOA)[2]。作为量子绝热算法[3]的参数化版本,QAOA利用量子现象(即绝热定理[4])来近似解决优化问题。由于许多研究表明,对于重要优化问题,QAOA相比经典最先进求解器具有改进的扩展性能[5,6,7],大量科学研究致力于实现大规模数值模拟,以实证探索可能的量子优势[8,9,10]。
当前大规模、无噪声量子电路模拟的标准依赖于通过GPU进行高效矩阵乘法,特别是cuStateVec SDK[11],它允许将Qiskit[12]、Pennylane[13]或其他SDK编写的电路指令转换为CUDA(用于在NVIDIA GPU上执行计算的工具包)[14]。
由于其特定的量子电路结构,模拟标准p深度、n量子比特、基于X混合器的QAOA电路的运行时复杂度为𝒪(p n 2^n),而一般p深度量子电路的复杂度为𝒪(p 4^n)[15]。由于我们预计X混合器的模拟不会有进一步的加速(参见[15,16]),并且为了允许任意混合器(参见[17]),我们专注于基于成本算子的对角结构实现加速增益(参见[15])。
在当前最先进的QAOA模拟器QOKit[15]中,Lykov等人通过并行预计算所有可能解的成本,并利用这些成本进行成本酉应用和期望值计算,从而利用了成本算子的对角结构。然而,QOKit是用Python编写的,因此无法原生使用CUDA,阻碍了其实现最快计算的可能性。更重要的是,除了成本哈密顿量的预计算外,其提供的代码中两个关键功能由于缺少实现而无法执行:cuStateVec模拟器和梯度计算[18]。
为弥补QOKit的不足,我们开发了一个基于CUDA的QAOA模拟器(CUAOA),该模拟器经过优化,可在原生CUDA中执行所有与QAOA评估实际相关的操作,面向单GPU设置。为确保与预期最终用户编程语言Python(例如通过PyO3[19])的兼容性,同时允许直接访问CUDA,我们使用Rust并集成C/C++模块(通过外部函数接口FFI)。与当前最先进技术类似,我们使用cuStateVec处理所有与成本酉无关的计算,例如混合器应用和采样过程。与当前最先进的QAOA模拟器相比,我们通过实现显著的加速,提出了以下CUDA原生实现:
• 成本哈密顿量的预计算,
• 成本酉的应用,
• 期望值的计算,以及
• 梯度计算。
本文的其余部分结构如下:第二部分概述了QAOA模拟、伴随微分法和CUDA的基础知识。第四部分介绍了CUAOA,随后在第五部分进行了评估。最后,第六部分总结了我们的发现。
II 背景
本节介绍QAOA、在经典模拟量子电路中高效计算梯度的方法以及CUDA的基础知识。
II.A 量子近似优化算法
给定一个由目标函数f: {0,1}^n → ℝ定义的组合优化问题,QAOA通过以下步骤近似最优解[2]:
-
将目标值映射到对角成本哈密顿量H_C = Σ_x f(x) |x⟩⟨x|的本征值上。
-
在混合器哈密顿量的基态中准备系统,通常对于H_M = -Σ_{i=1}^n σ_i^x,基态为|+⟩^{⊗n}。
-
近似模拟时间演化exp(i∫_0^T H_s(t) dt),其中H_s(t) = (1-s(t)) H_M + s(t) H_C控制绝热演化,且双射s: [0,T] → [0,1]对于给定T>0单调递增。
-
测量最终状态并将其重新映射到目标函数f的相应解上。
为了在量子电路中模拟H_s的时间演化,通过Trotter化将其离散化为p∈ℕ个哈密顿量H_s(1/T),..., H_s(T),形成以下构成QAOA的酉操作:
U(β,γ) = U_M(β_p) U_C(γ_p) ... U_M(β_1) U_C(γ_1) H^{⊗n}, (1)
其中β_i和γ_i控制时间演化的速度,U_M(β_i) = e^{-iβ_i H_M},U_C(γ_i) = e^{-iγ_i H_C},使得U(β,γ)在p→∞且恒定速度(即β_i=1-i/p,γ_i=i/p)时趋近于绝热时间演化[20]。
II.B 伴随微分法
伴随微分法[21]利用经典量子电路模拟器中克隆状态向量的可能性,将运行时降低至𝒪(P),而通常使用的参数移位规则复杂度为𝒪(P·m)[22],其中P是量子电路中可能参数化的层数,m是参数数量。这些复杂度表示模拟一层门应用的查询复杂度,对于一个n量子比特量子寄存器通常为𝒪(4^n)。
以下我们假设每个电路层U_i恰好有一个参数θ_i,这是QAOA标准形式的情况。关于该方法适用于涉及重复参数和每层多个参数的更一般电路层所需的调整细节,请参见参考文献[21,附录B]。值得注意的是,这些调整会增加运行时复杂度,但仅为常数因子。
伴随微分法利用测量算子M的偏导数的厄米性,即:
∂⟨M⟩/∂θ_i = ⟨0| U_1^† ... ∂U_i^†/∂θ_i ... U_P^† M U_P ... U_i ... U_1 |0⟩ + ⟨0| U_1^† ... U_i^† ... U_P^† M U_P ... ∂U_i/∂θ_i ... U_1 |0⟩ = 2ℜ(⟨0| U_1^† ... U_i^† ... U_P^† M U_P ... ∂U_i/∂θ_i ... U_1 |0⟩),
可写为∇{θ_i}⟨M⟩ = 2ℜ(⟨b_i| ∂U_i/∂θ_i |k_i⟩),其中⟨b_i| ≔ ⟨0| U_1^† ... U_i^† ... U_P^† M U_P ... U{i+1},|k_i⟩ ≔ U_{i-1} ... U_1 |0⟩可通过⟨b_{i+1}| = ⟨b_i| U_{i+1}^†和|k_{i+1}⟩ = U_i |k_i⟩递归计算。由于这种递归特性,计算∇_{θ_1}⟨M⟩需要𝒪(P)层执行,然后所有其他偏导数仅需𝒪(1)层执行,从而得出总运行时复杂度为𝒪(P)。
II.C CUDA
统一计算设备架构(CUDA)是一个并行计算平台和应用程序编程接口(API)模型,使开发人员能够直接访问NVIDIA图形处理单元(GPU)[14]。GPU相对于CPU的主要优势在于能够以大规模并行化的方式执行计算。这对于矩阵乘法等应用尤其相关,因为矩阵乘法可以分解为许多更小且独立的计算。
CUDA是C/C++编程语言的扩展,具有以线程为中心的层次结构。CPU通过内核函数(称为kernel)调用CUDA,这些kernel在GPU上运行。这些kernel由线程块网格执行,每个块包含多个线程。这种层次结构安排使得能够高效利用GPU资源,并精确控制每个线程的行为。同一块内的线程可以通过共享内存共享数据,共享内存对每个块是唯一的,通常比全局内存更快。不同块线程之间的通信通过全局内存进行[23]。
III 相关工作
虽然存在多个旨在提供QAOA各版本电路实现的框架(例如OpenQAOA [24]和JuliaQAOA [25]),但只有QOKit [15]致力于并通过GPU使用实现显著的加速。因此,在本节的后续部分,我们将重点关注QOKit。
QOKit旨在模拟涉及大量量子比特的QAOA,并通过OpenMPI [26]共享状态向量的信息,提供多GPU方法。QOKit的两个关键特性是成本算子的并行计算与应用,以及以𝒪(n 2^n)时间应用X混合器的算法。
在本文发表时,QOKit在其已发布的代码中存在显著缺陷,即缺少对cuStateVec电路模拟器的支持以及梯度计算功能,这两者都是实现最短运行时间的关键组件。此外,QOKit的局限性在于其实现在Python中进行,这导致其提出的混合器酉操作以及基于OpenMPI的并行化性能比纯cuStateVec更差[15]。同时,为了提取状态向量的信息(例如用于采样),需要将状态向量的概率复制到CPU,这造成了显著的运行时瓶颈。
基于参考文献[15]中呈现的结果,与基于纯cuStateVec的实现相比,QOKit提供的唯一明确加速似乎是成本算子的高效预计算及其对角形式的应用。预计算基于目标函数的多项式表示:
f(s) = ∑{k=1}^L w_k ∏{i ∈ t_k} s_i, (2)
其中s ∈ {-1,1}^n,且𝒯 ≔ {(w_1, t_1), ..., (w_L, t_L)}通过所涉及变量的索引t_k ⊆ {i | 1 ≤ i ≤ n}及其相关权重w_k ∈ ℝ定义多项式项。为了计算所有可能输入s的f(s),在GPU上分配一个零数组,然后对数组中的每个条目并行应用一个遍历𝒯中所有项的GPU内核。每个项的值使用按位异或和种群计数操作计算,以确定∏_{i ∈ t_k} s_i的符号。成本酉的应用通过状态向量与exp(-i γ_i f(s))的逐元素乘积执行。
IV 方法论
为了利用QAOA中成本算子的对角结构,我们现在提出CUAOA,一个CUDA加速的、单GPU量子电路模拟器,用于QAOA,它消除了QOKit的缺点。为了向最终用户提供与QOKit相同的便利性------Python接口------同时实现无缝的CUDA可操作性,CUAOA的核心模块使用Rust编写。这允许通过FFI访问用C/C++编写的CUDA指令,并通过PyO3 [19]等库从Python内部集成。与Python实现相比,这还带来了显著的优势,即运行完全相同的程序指令要快得多,仅仅因为Rust是一种编译语言,即代码在执行前直接编译为机器码。
从与电路无关的无噪声量子电路模拟的最新技术(即cuStateVec)为基准出发,我们现在展示如何通过基于CUDA实现成本算子的对角形式,使涉及成本算子的每个电路模拟组件都能更高效地实现。
IV.A 成本函数表示
在标准的QAOA模拟中,成本算子通过模拟成本函数的量子门表示。然而,由于成本算子在大多数实际应用中对角(这是基编码的结果),在经典电路模拟中,成本算子的应用可以直接通过与对角矩阵的乘法执行,这可以在GPU上完全并行化。
改进QOKit [15]的成本函数计算,我们使用基于0-1的函数表示,显著减少了必要的加法次数:使用独热编码对n个二进制变量的索引进行编码,我们可以将多项式目标函数表示为:
f(x) = ∑_{k=1}^L w_k (x ⇔ x ∧b [∑{v_i ∈ t_k} 2^i]_2), (3)
其中每个项t_k由变量索引v_i ∈ [n]组成,且⇔表示逻辑等价,分别产生1或0。由于二进制字符串[∑_{v_i ∈ t_k} 2^i]_2可以通过每个项t_k的独热表示的按位逻辑与操作(记为∧_b)轻松计算,并且对于任何给定的x,只需考虑二进制串x非零的条目,因此在计算中可以忽略大量项。QOKit没有利用这个捷径,而是遍历所有项。因此,对于具有大量低阶项的多项式(在实践中甚至成为常态),我们的方法可以显著更快。对于具有对称性的问题(例如MaxCut问题),许多成本值彼此相等,从而可能获得额外的加速。然而,为了避免破坏问题的通用性,我们未进行此类优化。
IV.B QAOA电路模拟
CUAOA首先为状态向量和成本哈密顿量分配内存,并存储引用相应GPU内存的指针。此外,创建一个CUDA流,并将其引用存储在句柄中,这允许在同一GPU上并行执行与不同流关联的多个内核。进一步,使用句柄的流初始化与cuStateVec库交互的句柄,并随后存储。其他变量的内存在句柄初始化时不会分配,只在实际需要时才分配,以减少内存使用。
状态向量被初始化为CUDA复数类型cuDoubleComplex的数组,并行初始化每个条目。由于所有评估都是针对使用X混合器的QAOA标准形式进行的,我们直接将数组的所有值初始化为1/√(2^n)。成本哈密顿量被初始化为双精度条目的数组,每个条目的值通过公式3并行计算。成本酉应用于状态向量|ψ⟩,利用欧拉公式exp(iθ) = cos(θ) + i sin(θ),通过ψ_i ↦ [cos(-γ_i f(x)) + i sin(-γ_i f(x))] · ψ_i实现。变分参数γ_i作为双精度输入传递给此操作,并使用CUDA内置的乘法函数cuCmul。请注意,虽然cuStateVec也提供了直接应用对角矩阵1的函数1,即custatevecApplyGeneralizedPermutationMatrix。,但它们不支持γ_i的原地乘法,这将不得不通过另一个内核完成,导致资源效率低下,因此证明了所述方法的必要性。
为了应用混合器酉,使用custatevecApplyMatrix。由于我们在评估中仅使用X混合器,这简化为对每个量子比特应用R_x(-2β_i)门。
IV.C 梯度计算
为了计算QAOA电路对其变分参数γ和β的梯度,我们采用第二-B节中概述的伴随微分技术,因为这是经典电路模拟中梯度计算的最新技术。对于QAOA,每层梯度计算的另一个简化源于众所周知的恒等式∂/∂t e^{tA} = A e^{tA},这意味着∂/∂t e^{-iγ_i H_C} = -i H_C e^{-iγ_i H_C}和∂/∂t e^{-iγ_i H_M} = -i H_M e^{-iγ_i H_M}。虽然H_C的应用是简单的,但H_M的应用在我们的所有评估运行中都简化为一层X门,因为我们只考虑标准的X混合器。第二-B节中描述的每个梯度计算步骤所需的去计算也基于∂/∂t e^{tA} = A e^{tA}简化,因为只需要分别去计算-i H_M和-i H_C。由于这两个算子都是厄米的(即H_M = H_M^†和H_C = H_C^†),这种去计算可以通过分别应用i H_M和i H_C完成。在我们的实现中,我们通过从实部切换到虚部来摆脱引入的虚数i(参见第二-B节)。
IV.D 从GPU检索结果
QAOA模拟器最重要的输出无疑是期望值⟨ψ|H_C|ψ⟩ = ∑_{i=1}^{2^n} f(x_i) |ψ_i|^2。为了计算这个和,我们基于结果QAOA状态向量|ψ⟩和成本算子,对所有i计算f(x_i) |ψ_i|^2,并将结果存储在一个新的双精度数组中。然后,我们通过将该数组分解为树状层次结构来计算其所有分量的和,在每个层级中,总是并行添加两个元素,总共进行log_2(2^n)次顺序计算。
为了从状态向量中采样,我们使用cuStateVec中提供的采样功能。这具有巨大的优势,即状态向量无需复制到CPU,从而避免了任何内存转换瓶颈。除了采样的解比特串,我们还输出相应的目标值,因为它已经存储在GPU上,从而为用户节省了额外的计算努力。此外,我们的实现还支持将完整状态向量从GPU导出到CPU的边缘情况。
V 评估
为评估CUAOA的性能,我们检查其在完整电路执行中输出期望值以及采样的运行时间,并考察其在基于梯度的参数训练中的性能。
与QOKit的评估[15]保持一致,我们考虑包含6到29个顶点的三类图的MaxCut问题:(1) 基于Erdős-Rényi G(n,p)模型[27]生成的连通度为25%、50%和75%的随机图;(2) 随机3-正则图;(3) 完全图。每顶点数和图类型(将每个Erdős-Rényi连通度视为独立类型)生成五个实例,得到一个包含444个图的数据集。
作为基准,我们采用了当前最先进的HPC QAOA模拟器QOKit,以及Qiskit和Pennylane中的标准QAOA实现。对于Qiskit和Pennylane,使用cuStateVec在GPU上运行实验。QOKit的电路模拟基于numba(通过即时编译将Python代码转换为机器码,并可原生在GPU上运行[28]),因为QOKit的cuStateVec变体在当前可用的代码版本中未实现。虽然这限制了我们结果与已发表的QOKit结果的可比性,但我们的方法表明,即使QOKit的cuStateVec可执行,我们对QAOA模拟的所有修改都产生了理论证明优于QOKit的改进。
所有实验均在一个高端消费级系统上运行,该系统运行EndeavourOS Linux x86_64,Linux内核版本为6.8.7-arch1-1,配备64GB RAM、AMD Ryzen 7 3700X CPU(16核 @ 3.600 GHz)和NVIDIA GeForce RTX 3090 GPU。所有执行均从Python脚本内部启动。
V.A 单个QAOA电路模拟的运行时间
为了检查普通QAOA电路执行(以期望值测量结束)的运行时间,我们在图1中比较了CUAOA与三个基准(QOKit、Qiskit和Pennylane)。对于Pennylane,超过26个顶点的问题实例出现内存分配错误,导致仅成功运行了391个图。除了这个技术细节,我们可以观察到CUAOA在所有运行中表现最佳,甚至在所有中小型问题实例中,其性能比最先进的基准提升了数个数量级。显然,对于CUAOA,指数级运行时缩放效应仅在大约16量子比特时才开始显现。
与理论考虑一致,混合器酉的应用最终成为运行时的最大瓶颈,这可以通过比较图1与基于采样的QAOA运行结果(图2)看出,其中对于超过20量子比特的问题,所有模拟器的运行时斜率变得相同。阻碍进一步加速的主要原因是所有混合器门的顺序应用。由于每个混合器门的应用都会修改整个状态向量的内存,因此无法并行化。
最后,对于低于20量子比特的问题实例,CUAOA的运行时比QOKit快一个数量级,这必然是我们CUDA原生实现以及第四部分引入的优化计算的结果。对于超过20量子比特的问题实例,这种减少的开销显然变得微不足道,导致运行时间大致相等,但CUAOA仍优于QOKit。
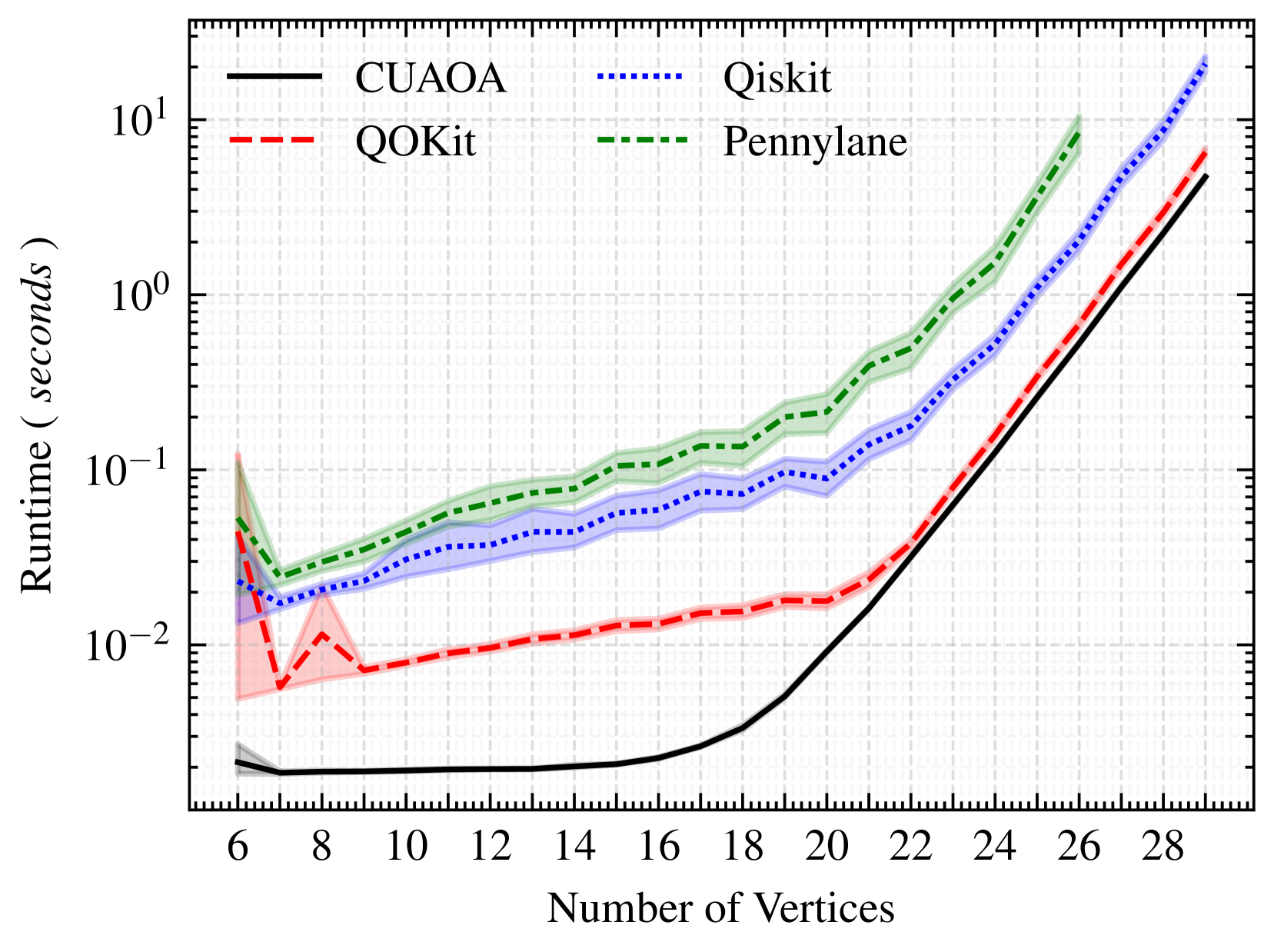
图1:p=6时QAOA关于期望值的运行时
为了评估从QAOA结果状态向量中采样比特串的运行时间,图2显示了p=6和1024次采样的QAOA运行结果。为了与QOKit进行更好的比较(本文发表时其可用实现不支持采样),我们实现了一个最小努力的Python脚本。为此,我们利用QOKit的功能将状态向量的概率提取到CPU。随后,我们使用标准的Python随机数生成器从包含关联累积概率(使用numpy的cumsum函数计算)的数组中采样。
CUAOA的结果与期望值的结果相符,显示了两者的高度效率,即未超过混合器应用的运行时。虽然Qiskit表现相当好,但Pennylane与期望值的运行时相比明显更差。其原因尚不完全清楚,但表明采样实现的不同,尤其是对于较小的电路规模。正如预期,一旦状态向量的维度增加,我们为QOKit实现的基于CPU的采样几乎没有竞争力。
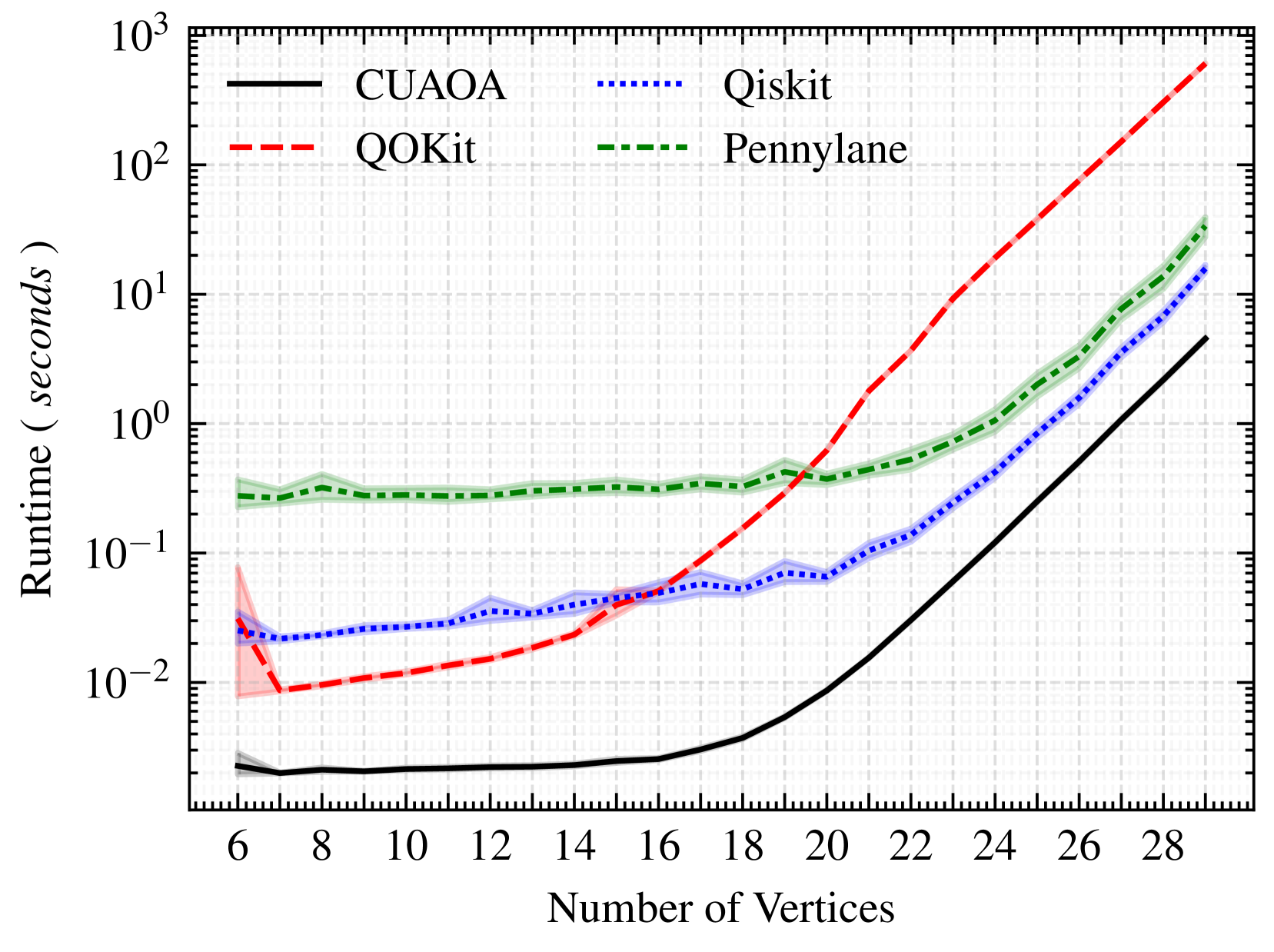
图2:1024次采样且p=6时的运行时
V.B 参数训练
研究基于梯度的参数训练,我们现在检查所有参数的梯度计算运行时。由于QOKit和基于cuStateVec的Qiskit实现在本文发表时的可用形式均不允许计算梯度,我们的实验仅限于Pennylane和CUAOA的比较。由于Pennylane实现也采用了伴随方法,这与我们针对QAOA优化的增强版伴随方法是一个公平的比较。与早期评估运行类似,Pennylane再次无法执行超过26个顶点的图,导致仅成功执行了391个问题实例。图3清楚地显示,对于最多18量子比特的问题实例,CUAOA的性能比Pennylane高出数个数量级,在几乎所有运行中快了大约100倍。对于更多量子比特,这一差距缩小到大约10倍加速,在大约18量子比特处运行时显著增加,类似于第五-A部分中普通电路评估所显现的情况。
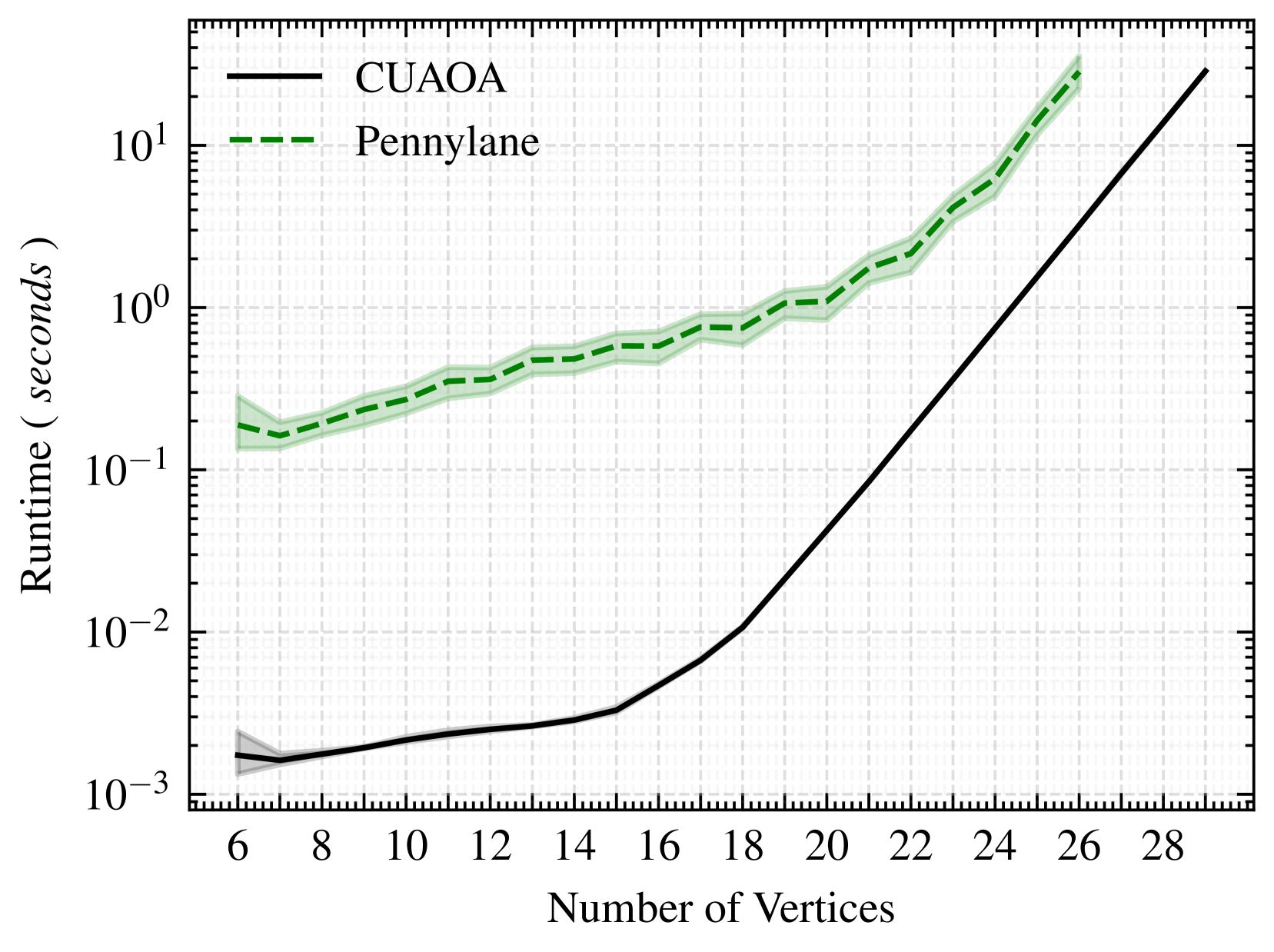
图3:使用伴随微分法(p=6)进行梯度计算的运行时
最后,我们还提供了基于梯度的优化器L-BFGS(原生)[29]和BFGS(通过scipy)[30]的实现。额外的实验(为简洁起见未在此展示)表明,当使用相同的优化器(BFGS)时,CUAOA仍然比Pennylane快多达两个数量级,基本上反映了图3的结果。
VI 结论
本文提出了一种面向单GPU使用的经典高性能基于CUDA的QAOA电路模拟器(CUAOA)。通过在QAOA模拟的多个阶段利用成本算子的对角结构实现加速,即(1)成本算子的计算与应用,(2)期望值的计算,以及(3)提供基于伴随微分法的QAOA专用梯度计算方法,我们提出的CUAOA实现在中小规模问题实例上比最先进的QAOA模拟器QOKit快一个数量级(即加速10倍)。对于超过20个量子比特的大规模问题实例,我们的方法也优于QOKit,但同样受到混合器算子主导运行时间的影响。值得注意的是,对于关键应用(1)从状态向量采样和(2)基于GPU的梯度计算,CUAOA提供的功能明显多于QOKit。此外,我们的梯度计算比相应的最先进方法快约两个数量级。总之,在代表性评估中,我们的方法在性能上超越所有基准多达数个数量级,可被视为单GPU QAOA模拟的新技术水平。
在未来的工作中,我们的方法可以扩展到多GPU场景,这主要需要额外的实现,同时依赖于相同的理论见解。此外,可以通过直接缩小搜索空间,原生实现保持约束的混合器,从而显著减少强约束问题的数值模拟运行时间。
致谢
本文部分资金由德国联邦经济事务和气候行动部通过资助计划"量子计算------工业应用"(基于"数字技术发展"拨款,合同编号:01MQ22008A)以及慕尼黑量子谷提供。慕尼黑量子谷由巴伐利亚州政府通过"巴伐利亚高科技议程增强版"基金支持。
References
[1]
J. Blenninger, J. Stein, D. Bucher, P. J. Eder et al., "CUAOA: A Novel CUDA-Accelerated Simulation Framework for the QAOA," Jul. 2024.
[2]
E. Farhi, J. Goldstone, and S. Gutmann, "A quantum approximate optimization algorithm," 2014.
[3]
E. Farhi, J. Goldstone, S. Gutmann, and M. Sipser, "Quantum computation by adiabatic evolution," 2000.
[4]
M. Born and V. Fock, "Beweis des Adiabatensatzes," Zeitschrift für Phys., vol. 51, no. 3, pp. 165--180, 1928.
[5]
S. Boulebnane and A. Montanaro, "Solving boolean satisfiability problems with the quantum approximate optimization algorithm," 2022.
[6]
R. Shaydulin, C. Li, S. Chakrabarti, M. DeCross et al., "Evidence of scaling advantage for the quantum approximate optimization algorithm on a classically intractable problem," Science Advances, vol. 10, no. 22, p. eadm6761, 2024.
[7]
C. Carlson, Z. Jorquera, A. Kolla, and S. Kordonowy, "A quantum advantage over classical for local max cut," 2023.
[8]
S. H. Sack and D. J. Egger, "Large-scale quantum approximate optimization on nonplanar graphs with machine learning noise mitigation," Phys. Rev. Res., vol. 6, p. 013223, Mar 2024.
[9]
M. Medvidović and G. Carleo, "Classical variational simulation of the Quantum Approximate Optimization Algorithm," npj Quantum Inf., vol. 7, no. 1, p. 101, 2021.
[10]
H. Shang, Y. Fan, L. Shen, C. Guo et al., "Towards practical and massively parallel quantum computing emulation for quantum chemistry," npj Quantum Inf., vol. 9, no. 1, p. 33, 2023.
[11]
H. Bayraktar, A. Charara, D. Clark, S. Cohen et al., "cuquantum sdk: A high-performance library for accelerating quantum science," in 2023 IEEE International Conference on Quantum Computing and Engineering (QCE). Los Alamitos, CA, USA: IEEE Computer Society, sep 2023, pp. 1050--1061.
[12]
A. Javadi-Abhari, M. Treinish, K. Krsulich, C. J. Wood et al., "Quantum computing with Qiskit," 2024.
[13]
V. Bergholm, J. Izaac, M. Schuld, C. Gogolin et al., "Pennylane: Automatic differentiation of hybrid quantum-classical computations," 2022.
[14]
NVIDIA Corporation, NVIDIA CUDA Compute Unified Device Architecture Programming Guide. NVIDIA Corporation, 2007.
[15]
D. Lykov, R. Shaydulin, Y. Sun, Y. Alexeev et al., "Fast simulation of high-depth qaoa circuits," in Proceedings of the SC '23 Workshops of The International Conference on High Performance Computing, Network, Storage, and Analysis, ser. SC-W '23. New York, NY, USA: Association for Computing Machinery, 2023, p. 1443--1451.
[16]
Fino and Algazi, "Unified matrix treatment of the fast walsh-hadamard transform," IEEE Transactions on Computers, vol. C-25, no. 11, pp. 1142--1146, 1976.
[17]
A. Bärtschi and S. Eidenbenz, "Grover mixers for qaoa: Shifting complexity from mixer design to state preparation," in 2020 IEEE International Conference on Quantum Computing and Engineering (QCE), 2020, pp. 72--82.
[18]
D. Lykov, R. Shaydulin, Y. Sun, Y. Alexeev et al., "GitHub repository QOKit," https://github.com/jpmorganchase/QOKit, 2024.
[19]
PyO3 Project and Contributors, "PyO3."
[20]
S. H. Sack and M. Serbyn, "Quantum annealing initialization of the quantum approximate optimization algorithm," Quantum, vol. 5, p. 491, Jul. 2021.
[21]
T. Jones and J. Gacon, "Efficient calculation of gradients in classical simulations of variational quantum algorithms," 2020.
[22]
K. Mitarai, M. Negoro, M. Kitagawa, and K. Fujii, "Quantum circuit learning," Phys. Rev. A, vol. 98, p. 032309, Sep 2018.
[23]
NVIDIA Corporation, "NVIDIA CUDA C programming guide," 2021.
[24]
V. Sharma, N. S. B. Saharan, S.-H. Chiew, E. I. R. Chiacchio et al., "Openqaoa -- an sdk for qaoa," 2022.
[25]
J. Golden, A. Baertschi, D. O'Malley, E. Pelofske et al., "Juliqaoa: Fast, flexible qaoa simulation," in Proceedings of the SC '23 Workshops of The International Conference on High Performance Computing, Network, Storage, and Analysis, ser. SC-W 2023. ACM, Nov. 2023.
[26]
R. L. Graham, T. S. Woodall, and J. M. Squyres, "Open mpi: A flexible high performance mpi," in Parallel Processing and Applied Mathematics, R. Wyrzykowski, J. Dongarra, N. Meyer, and J. Waśniewski, Eds. Berlin, Heidelberg: Springer Berlin Heidelberg, 2006, pp. 228--239.
[27]
P. Erdős and A. Rényi, "On random graphs. I." Publicationes Mathematicae Debrecen, vol. 6, no. 3-4, pp. 290--297, Jul 1959.
[28]
S. K. Lam, A. Pitrou, and S. Seibert, "Numba: a llvm-based python jit compiler," in Proceedings of the Second Workshop on the LLVM Compiler Infrastructure in HPC, ser. LLVM '15. New York, NY, USA: Association for Computing Machinery, 2015.
[29]
D. C. Liu and J. Nocedal, "On the limited memory BFGS method for large scale optimization," Math. Program., vol. 45, no. 1, pp. 503--528, 1989.
[30]
J. Nocedal, "Updating quasi newton matrices with limited storage," Mathematics of Computation, vol. 35, no. 151, pp. 951--958, Jul. 1980.
https://arxiv.org/html/2407.13012v1