2026.2.1周报 - 技术栈

2026.2.1 周报

文献阅读
- 摘要
- 创新点
- 网络框架
- - [多变量 VQC 适应策略](#多变量 VQC 适应策略)
  - [iQTransformer 架构](#iQTransformer 架构)
- 实验结果
- - 预测性能对比
  - 重构与长期预测
- 结论
- 不足
实验
量子计算学习笔记
- [Deutsch-Jozsa 算法](#Deutsch-Jozsa 算法)
- [Simon 算法](#Simon 算法)
- 量子傅里叶变换
- 总结
- 量子相位估计

文献阅读

题目： 《Quantum Neural Network Architectures for Multivariate Time-Series Forecasting》
期刊/会议： arXiv preprint
作者： S. Ranilla-Cortina, D. A. Aranda, J. Ballesteros, J. Bonilla, N. Monriob, Elías F. Combarro, J. Ranilla
发表时间： 2025
文章链接： https://arxiv.org/abs/2510.21168

摘要

本文针对量子机器学习在多变量时间序列预测中的应用挑战，提出了一系列解决方案。作者首先设计了将传统的单变量变分量子线路（VQC）扩展到多变量场景的适应性策略，探索了纯量子和混合量子-经典架构。在此基础上，文章提出了一种名为 iQTransformer 的新型量子 Transformer 架构，该架构将量子自注意力机制集成到 iTransformer 框架中，实现了对变量间依赖关系的量子化建模。作者在合成数据集和真实世界数据集上进行了广泛的实证评估。结果表明，量子模型在某些情况下能够以更少的可训练参数和更快的收敛速度，达到与最先进的经典模型相当甚至更优的预测精度。

创新点

提出了 iQTransformer 混合架构，它将量子自注意力神经网络嵌入到 iTransformer 框架中。不同于传统 Transformer 关注时间步之间的依赖，该架构利用量子纠缠和干涉特性，在特征空间中高效捕捉不同变量之间的复杂相互依赖关系。
针对 VQC 通常局限于单变量处理的问题，文章提出了多种将其扩展到多变量预测的策略，包括独立通道 VQC、密集嵌入、编码器-解码器 VQC 以及混合架构，并对这些策略进行了基准测试。
iQTransformer 等量子增强模型在保持高性能的同时，往往具有比同类经典模型更少的参数量，并且在训练过程中展现出更快的收敛特性，。

网络框架

本文框架主要包含两部分：一是多变量 VQC 的基础构建策略，二是核心的 iQTransformer 架构。

多变量 VQC 适应策略

为了处理多变量输入，作者设计了不同的 VQC 架构变体，分别如下：
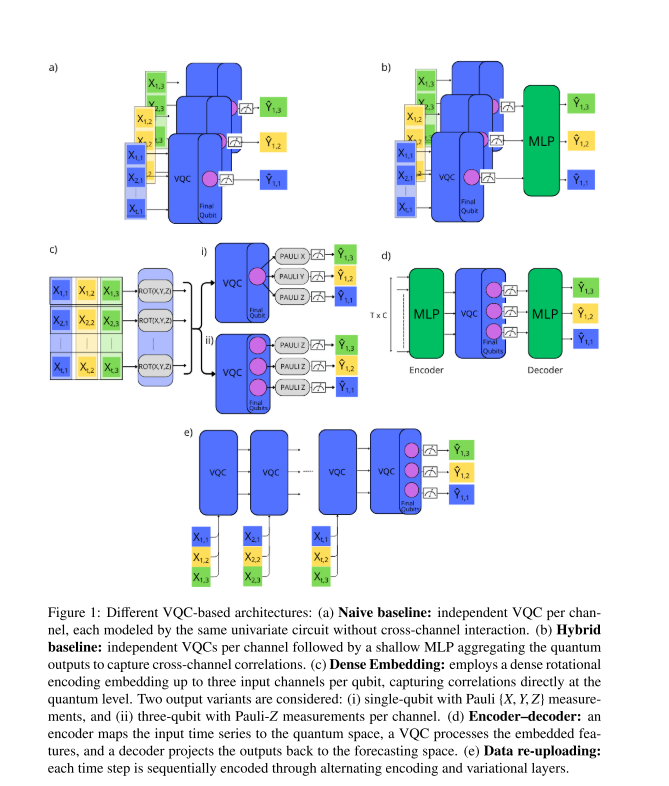
独立 VQC ，即为每个变量分配独立的 VQC，忽略变量间的相关性；
混合 VQC+MLP ，利用 VQC 提取特征，再通过经典 MLP 混合信息；
密集嵌入，将多个时间步压缩编码到量子态中。

图 1展示了基于 VQC 的不同多变量架构示意图。

iQTransformer 架构

这是本文的核心模型，基于 iTransformer 的倒置结构，对变量而非时间步进行嵌入。通过输入的多变量序列首先经过独立的时间序列嵌入，然后进入量子自注意力层处理变量间的关联，最后通过前馈网络输出预测结果。
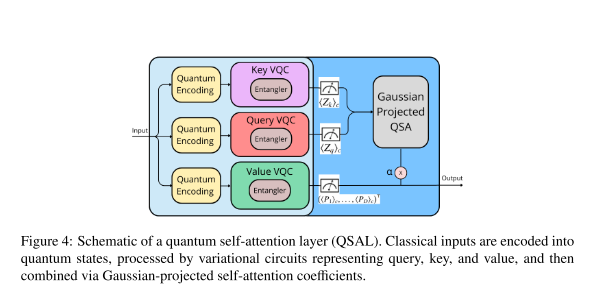
量子自注意力层 是利用参数化量子线路实现查询、键和值的计算与注意力聚合。

图 3展示了iTransformer/iQTransformer 预测流程示意图，每个变量被独立嵌入为 token，通过注意力机制处理变量间的相关性，最后进行投影输出

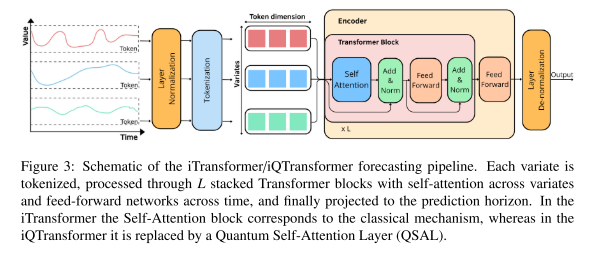
图4则说明了量子自注意力层的详细结构，展示了经典输入如何编码到量子态，并通过量子线路演化计算注意力分数。

实验结果

作者使用了两个数据集进行评估：

Lorenz 数据集：一个经典的混沌动力系统，用于测试模型对非线性动态的捕捉能力。
ITER 数据集：来自国际热核聚变实验堆的真实传感器数据，具有高维、复杂的特征。

预测性能对比

实验对比了包括 1D CNN、QGRU、iTransformer 和 iQTransformer 在内的多种模型在不同预测步长下的表现。

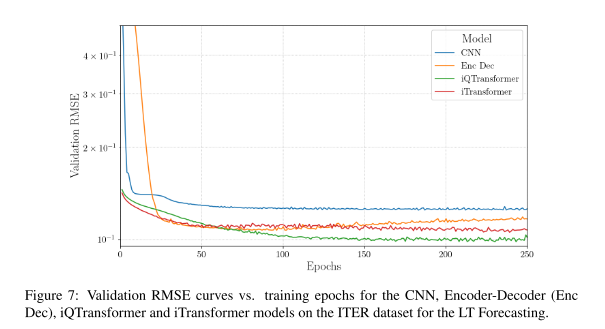
在短期预测中，Transformer 类模型表现最佳。iQTransformer 在 Lorenz 数据集上实现了极具竞争力的 RMSE，且参数量显著少于经典 Transformer。图 7 展示了验证集 RMSE 随训练 Epoch 的变化，iQTransformer 展现出极快的收敛速度，在早期 Epoch 就能达到较低的误差水平。

重构与长期预测

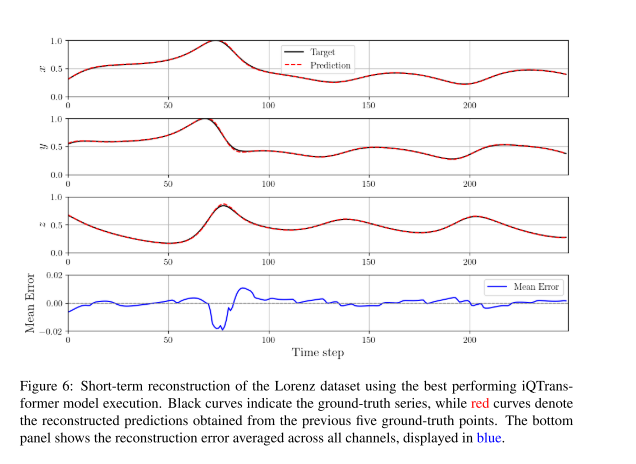
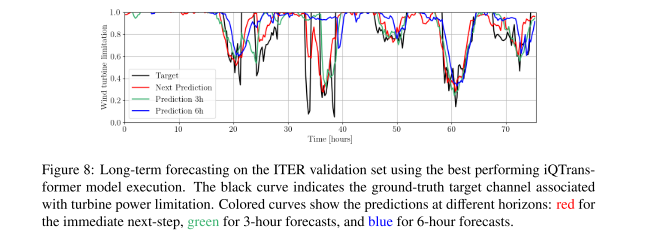
为了直观评估模型性能，作者展示了模型对 Lorenz 系统轨迹的重构以及对 ITER 数据的长期预测结果。iQTransformer 能够精准地跟随 Lorenz 吸引子的复杂轨迹，并且在 ITER 数据的长期预测中，也能较好地拟合真实值的趋势，优于部分简单的 VQC 基线。

使用表现最佳的 iQTransformer 对 Lorenz 数据集进行的短期重构结果。展示了预测轨迹与真实轨迹的高度重合

iQTransformer 在 ITER 验证集上的长期预测结果。展示了模型在多步预测任务中对复杂真实信号的拟合能力

结论

本文成功将量子机器学习扩展到了多变量时间序列预测领域。通过系统的基准测试，验证了 VQC 及其变体在处理多维数据时的潜力。提出的 iQTransformer 结合了经典 iTransformer 的结构优势与量子计算在特征空间处理上的强表达能力，不仅在预测精度上能够匹敌最先进的经典模型，还在参数效率和收敛速度上展现出独特的优势。这表明量子增强架构有望成为未来高效处理复杂多变量时序数据的有力工具。

不足

当前实验主要在无噪声模拟器上进行，未充分考虑含噪中尺度量子设备的噪声对注意力机制计算精度的影响；量子线路的模拟在经典计算机上计算成本高昂，且随着量子比特数增加，在真实硬件上的可扩展性仍需验证。

实验

本周复现了《Quantum Neural Network Architectures for Multivariate Time-Series Forecasting》的实验，目的是为了后面研究量子时序预测模型，并用自己的数据集做了验证，为后面模型的建立打下一个良好的基础。

这篇文章采用了iTransformer模型地采用了Inverted Tokenization机制，将每个变量视为一个 Token，并通过量子自注意力层利用量子纠缠和高斯核函数来捕获变量间的复杂相关性。
QSAL.py

这个源码定义了 iQTransformer 的核心量子层，通过量子电路计算变量间的注意力权重
代码的核心如下 ：

quantum_attention_circuit() 是核心量子节点，其利用 R y R_y Ry 旋转门将经典特征编码到量子态，并通过测量 PauliZ 期望值来提取特征表示。

QSAL Layer是量子自注意力层，其利用两个变量测量值之间的指数距离（高斯核）生成注意力矩阵，实现了 O ( C 2 ) O(C^2) O(C2) 的变量间相关性建模。

这种架构允许模型在量子空间中评估变量的重要性，尤其适合处理具有高度相关性的多元时序数据。

python 复制代码

import pennylane as qml
import torch
import torch.nn as nn

def quantum_attention_circuit(inputs, weights):
    """
    QSAL 核心电路：用于提取变量的量子特征表示
    Args:
        inputs: 经过 Embedding 后的变量特征向量 (D,)
        weights: 可训练的变分参数 (n_layers, n_qubits, 3)
    """
    n_qubits = len(inputs)
    n_layers = weights.shape[0]

    # 特征编码层：将经典向量映射到量子态
    for i in range(n_qubits):
        qml.RY(inputs[i], wires=i)

    # 变分层：通过纠缠和旋转增加模型表达能力
    for l in range(n_layers):
        for i in range(n_qubits - 1):
            qml.CNOT(wires=[i, i + 1])
        qml.CNOT(wires=[n_qubits - 1, 0])
        
        for i in range(n_qubits):
            qml.Rot(*weights[l, i], wires=i)

    # 测量层：返回 PauliZ 期望值作为该 Token 的量子嵌入表示
    return [qml.expval(qml.PauliZ(wires=i)) for i in range(n_qubits)]

class QSAL(nn.Module):
    def __init__(self, n_qubits, n_layers):
        super().__init__()
        dev = qml.device("default.qubit", wires=n_qubits)
        self.qnode = qml.QNode(quantum_attention_circuit, dev, interface="torch")
        
        # 定义量子权重
        q_weights_shape = {"weights": (n_layers, n_qubits, 3)}
        self.q_layer = qml.qnn.TorchLayer(self.qnode, q_weights_shape)

    def forward(self, x):
        """
        Args: x 形状为 (Batch, C, D), C 是变量数, D 是特征维度
        Returns: 注意力权重矩阵 (Batch, C, C)
        """
        batch_size, n_vars, _ = x.shape
        # 计算每个 Token 的量子特征向量 Z
        z = torch.stack([self.q_layer(x[:, i, :]) for i in range(n_vars)], dim=1) 
        
        # 基于高斯核计算相关性矩阵: aslpha_{i,j} = exp(-||z_i - z_j||^2)
        # 这里简化展示核心逻辑
        attn_matrix = torch.exp(-torch.cdist(z, z, p=2)**2)
        return attn_matrix

iQTransformer.py

该类整合了经典嵌入层、量子自注意力层和预测头，支持动态变量数 C C C 和时间步 T T T。它首先将时间维度压缩为固定长度的特征向量，然后通过量子层计算变量间的权重，最后输出目标变量的预测值。

python 复制代码

import torch
import torch.nn as nn

class iQTransformer(nn.Module):
    """
    iQTransformer 主模型：支持 Data-Agnostic 架构
    """
    def __init__(self, n_vars, input_dim, embed_dim, output_dim, n_qubits, n_layers):
        super().__init__()
        self.n_vars = n_vars
        
        # 1. 经典 Embedding：将时间维度 T 映射到量子位能接受的维度 D
        self.embedding = nn.Linear(input_dim, n_qubits)
        
        # 2. 量子自注意力层
        self.qsal = QSAL(n_qubits, n_layers)
        
        # 3. 预测头：映射到目标输出 (TEM, PRS, RHU, etc.)
        self.head = nn.Sequential(
            nn.Linear(n_qubits, 32),
            nn.ReLU(),
            nn.Linear(32, output_dim)
        )

    def forward(self, x):
        # x: (Batch, T, C) -> 转置为 (Batch, C, T)
        x = x.transpose(1, 2)
        
        # 映射时间特征: (Batch, C, T) -> (Batch, C, n_qubits)
        e = self.embedding(x)
        
        # 获取量子注意力权重
        attn = self.qsal(e) 
        
        # 聚合特征并预测
        # 此处简化：将注意力作用于原始嵌入并输出
        out = torch.matmul(attn, e) 
        return self.head(out[:, :6, :]) # 仅输出 6 个核心变量的预测

以上是部分核心代码，具体需要可以自行去复现

我的复现结果如下：iQTransformer 的性能略逊于经典 Transformer。

后面反思了一下原因，可能是我的量子电路存在梯度消失现象，且由于变量间采用复杂的量子核函数计算相关性，其收敛速度显著慢于经典的点积注意力机制。量子仿真模拟的计算成本极高，用少量的qbit可能会，限制了在大规模参数搜索和深层架构堆叠上的表现，难以发挥量子纠缠的潜在优势。

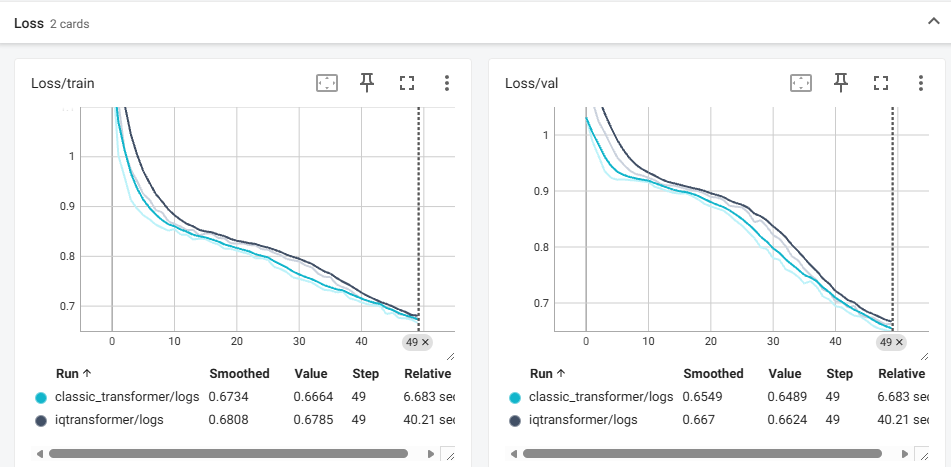
因此后续打算对这个模型进行进一步的调优，解决量子模型的梯度问题。

量子计算学习笔记

这周学习了量子计算在常见几个算法上的计算优势。

Deutsch-Jozsa 算法

Deutsch-Jozsa 算法是常数与平衡函数问题，其展示量子并行性超越经典算法的第一个范例，解决了所谓的赌意识（Deutsch）及其推广问题。
问题定义 ：给定一个布尔函数 f : { 0 , 1 } n → { 0 , 1 } f: \{0,1\}^n \rightarrow \{0,1\} f:{0,1}n→{0,1}，已知它要么是常数函数 ，即对所有输入输出相同，要么是平衡函数 ，一半输入输出 0，另一半输出 1。目标是判定其类型。

复杂度对比：

经典算法：在最坏情况下，需要查询 2 n − 1 + 1 2^{n-1} + 1 2n−1+1 次才能给出 100% 确定的答案。
量子算法：仅需 1 次 查询。

量子算法的核心是利用 Hadamard 门创建叠加态，通过函数 f f f 的量子谕示（Oracle）产生相位反转。作用后的状态： ∣ ψ ⟩ = 1 2 n ∑ x ∈ { 0 , 1 } n ( − 1 ) f ( x ) ∣ x ⟩ |\psi\rangle = \frac{1}{\sqrt{2^n}} \sum_{x \in \{0,1\}^n} (-1)^{f(x)} |x\rangle ∣ψ⟩=2n 1∑x∈{0,1}n(−1)f(x)∣x⟩。再次施加 H ⊗ n H^{\otimes n} H⊗n 门后，若 f f f 为常数，测量得到 ∣ 0 ⟩ ⊗ n |0\rangle^{\otimes n} ∣0⟩⊗n 的概率为 1；若 f f f 为平衡，测量得到该态的概率为 0。

Simon 算法

Simon 算法是一个定义在布尔函数上的问题，要求找到一个特定的隐藏字符串 s s s。

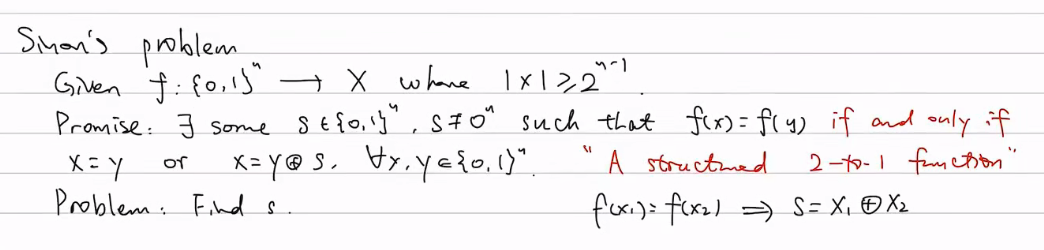
问题定义 ：函数 f f f 满足 f ( x ) = f ( y ) f(x) = f(y) f(x)=f(y) 当且仅当 x = y x = y x=y 或 x = y ⊕ s x = y \oplus s x=y⊕s。
复杂度分析：

经典算法：查询复杂度为 2 n / 2 2^{n/2} 2n/2 次查询，成功概率为 2 / 3 2/3 2/3。
量子算法：通过重复查询 n n n 次，查询复杂度为 n ⋅ log ⁡ ( 1 / δ ) n \cdot \log(1/\delta) n⋅log(1/δ)，成功概率为 1 − δ 1-\delta 1−δ。
量子算法每次测量得到一个满足条件的 y y y，使得 s ⋅ y ( m o d 2 ) = 0 s \cdot y \pmod 2 = 0 s⋅y(mod2)=0。通过构建线性独立方程组，可以解出 s s s 的值。

量子傅里叶变换

QFT 是量子计算中的一种重要变换，类似于经典傅里叶变换，但在量子层面上进行。

QFT 将计算基 ∣ x ⟩ |x\rangle ∣x⟩ 映射到频率基 ∣ y ⟩ |y\rangle ∣y⟩：
Q F T ∣ x ⟩ = 1 2 n ∑ y = 0 2 n − 1 e 2 π i x y 2 n ∣ y ⟩ QFT|x\rangle = \frac{1}{\sqrt{2^n}} \sum_{y=0}^{2^n-1} e^{2\pi i \frac{xy}{2^n}} |y\rangle QFT∣x⟩=2n 1y=0∑2n−1e2πi2nxy∣y⟩

在 Z 2 n \mathbb{Z}_2^n Z2n 上，QFT 可以看作是 n n n 个 Hadamard 门的张量积。

QFT 可以通过受控相位门和 Hadamard 门来实现。QFT 的复杂度为 O ( n 2 ) O(n^2) O(n2)，仅与输入大小 n n n 的平方相关，在量子计算中非常高效。

总结

经典 vs 量子复杂度

问题类型	经典算法复杂度	量子算法复杂度	技术
Deutsch-Jozsa	2 n − 1 + 1 2^{n-1}+1 2n−1+1	1 1 1	相位回传 (Phase Kickback)
Simon (三问问题)	O ( 2 n / 2 ) O(2^{n/2}) O(2n/2)	O ( n ) O(n) O(n)	线性方程组 + 叠加态
傅里叶变换	O ( n 2 n ) O(n 2^n) O(n2n) (FFT)	O ( n 2 ) O(n^2) O(n2)	QFT 线路

量子相位估计

相位估计问题用于估计一个算符特征值的相位 θ \theta θ。
特殊情况 ：当相位 θ \theta θ 是 2 π 2\pi 2π 的幂次方时，可以通过移动小数点来精确估计。
逆变换应用 ：量子傅里叶变换的逆变换实现了从 y y y 基到 x x x 基的映射，逐步恢复出每个比特的信息。
哈德玛测试 ：这是一种简单的量子线路，用于估计相位。线路包括 Hadamard 门和受控 U U U 变换门，通过测量结果来提取相位信息。