1、回顾
1957年,弗兰克·罗森布拉特(Frank Rosenblatt)提出了感知机模型,他的工作证明了通过简单单元的互联和简单的学习规则,可以涌现出强大的智能行为,这一核心思想至今未变。
弗兰克·罗森布拉特(1928-1971)是一位美国心理学家和计算机科学家,他在康奈尔航空实验室工作。他深受早期神经科学研究(如沃伦·麦卡洛克和沃尔特·皮茨的神经元模型)和赫布学习理论的影响。他的目标不仅仅是构建一个模式识别机器,更是想通过机器模型来理解大脑的学习机制。
这是第一个可以从数据中学习并进行模式分类的算法模型,被公认为是人工神经网络的起点。感知机虽简单且有局限,但它标志着机器学习从逻辑推理走向连接主义(Connectionism)的新纪元。
2、核心思想
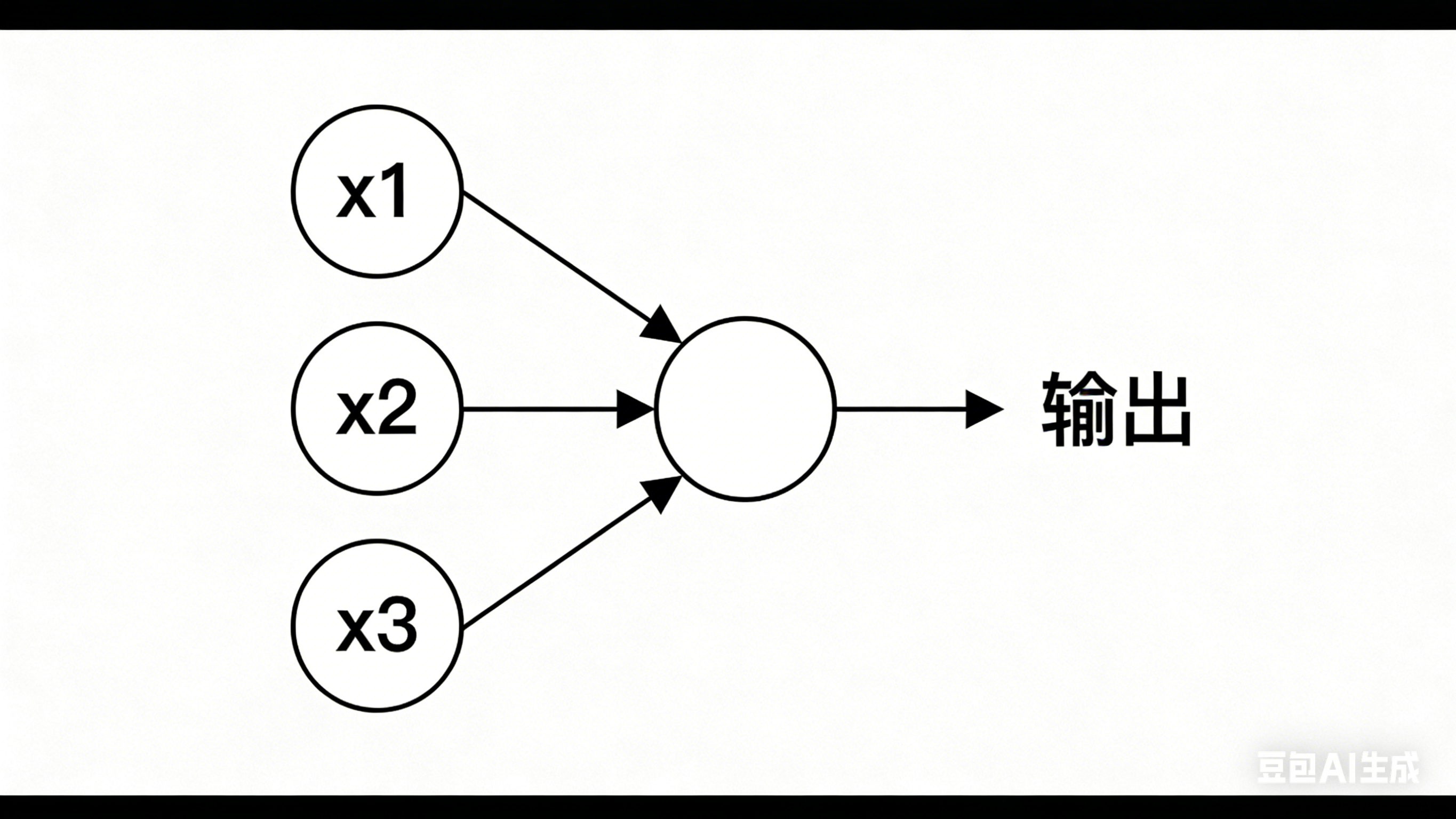
感知机模拟了生物神经元的基本工作原理:
1.输入 :接收多个输入信号 w 1 、 w 2 、 w 2 . . . w n w_1、w_2、w_2...w_n w1、w2、w2...wn。这些输入可以是任何特征数据,比如图片的像素值、文本的词向量、样本的属性。
2.加强求和 :每个输入都有一个对应的权重( w 1 、 w 2 、 w 2 . . . w n w_1、w_2、w_2...w_n w1、w2、w2...wn),用于衡量每个输入特征对最终决策的影响程度。神经元计算所有输入与权重的乘积之和。
3.激活:将加权和与一个阈值(或偏置)进行比较,通过一个激活函数产生输出。
- 如果加权和 >阈值(threshold),输出 1(代表"激活"或某一类)。
- 如果加权和 ≤ 阈值(threshold),输出 0(代表"抑制"或另一类)。
权重的取值不是固定的,感知机的"学习过程",本质上就是调整这些权重,让决策结果更准确。
3、数学表达
数学表达主要包括两个部分:加权求和 和 激活函数。
3.1加权求和(Linear Combination)
给定输入向量 x = [ x 1 , x 2 , ... , x n ] \mathbf{x} = [x_1, x_2, \dots, x_n] x=[x1,x2,...,xn],权重向量 w = [ w 1 , w 2 , ... , w n ] \mathbf{w} = [w_1, w_2, \dots, w_n] w=[w1,w2,...,wn],以及偏置项 b b b,感知机首先计算输入的加权和:
z = ∑ i = 1 n w i x i + b z = \sum_{i=1}^{n} w_i x_i + b z=i=1∑nwixi+b
也可以用向量内积的形式表示为:
z = w T x + b z = \mathbf{w}^T \mathbf{x} + b z=wTx+b
其中:
- z z z 是线性组合的结果(净输入);
- w T x \mathbf{w}^T \mathbf{x} wTx 表示权重与输入的点积;
- b b b 是偏置项,用于调整决策边界的位置。
3.2激活函数(Activation Function)
感知机通常使用阶跃函数(Step Function)作为激活函数。常见形式如下:
形式一:输出为 0 或 1
a = f ( z ) = { 1 , if z ≥ 0 0 , if z < 0 a = f(z) = \begin{cases} 1, & \text{if } z \geq 0 \\ 0, & \text{if } z < 0 \end{cases} a=f(z)={1,0,if z≥0if z<0
形式二:输出为 -1 或 1
a = f ( z ) = { 1 , if z ≥ 0 − 1 , if z < 0 a = f(z) = \begin{cases} 1, & \text{if } z \geq 0 \\ -1, & \text{if } z < 0 \end{cases} a=f(z)={1,−1,if z≥0if z<0
a a a 是感知机的最终输出。
完整表达式
感知机的整体输出可表示为:
a = f ( w T x + b ) 其中 f ( z ) = { 1 , z ≥ 0 0 ( 或 − 1 ) , z < 0 \boxed{ a = f(\mathbf{w}^T \mathbf{x} + b) \quad \text{其中} \quad f(z) = \begin{cases} 1, & z \geq 0 \\ 0 \ (\text{或 } -1), & z < 0 \end{cases} } a=f(wTx+b)其中f(z)={1,0 (或 −1),z≥0z<0
说明:
- 感知机适用于线性可分问题。
- 原始感知机使用不可导的阶跃函数,因此不能使用梯度下降直接训练;现代神经网络多采用 Sigmoid、ReLU 等可导激活函数。
- 感知机通过迭代更新权重和偏置来学习:
4、阈值(threshold)和偏置(bias)
在感知机模型中,阈值(Threshold) 和 偏置(Bias) 是密切相关的概念。虽然它们出现在不同的表达形式中,但实际上描述的是同一个机制的不同视角。
4.1阈值与偏置的数学关系
1.使用"阈值"的原始形式
早期感知机定义为:
y = { 1 , if ∑ i = 1 n w i x i ≥ θ 0 , otherwise y = \begin{cases} 1, & \text{if } \sum_{i=1}^n w_i x_i \geq \theta \\ 0, & \text{otherwise} \end{cases} y={1,0,if ∑i=1nwixi≥θotherwise
- θ \theta θ:称为 阈值(threshold)
- 只有当加权输入之和达到或超过 θ \theta θ 时,神经元才被激活(输出 1)
2. 转换为"偏置"形式
将不等式变形:
∑ i = 1 n w i x i ≥ θ ⇒ ∑ i = 1 n w i x i − θ ≥ 0 \sum_{i=1}^n w_i x_i \geq \theta \quad \Rightarrow \quad \sum_{i=1}^n w_i x_i - \theta \geq 0 i=1∑nwixi≥θ⇒i=1∑nwixi−θ≥0
令:
b = − θ b = -\theta b=−θ
则上式变为:
∑ i = 1 n w i x i + b ≥ 0 \sum_{i=1}^n w_i x_i + b \geq 0 i=1∑nwixi+b≥0
此时感知机输出可写为:
y = { 1 , if w T x + b ≥ 0 0 , otherwise y = \begin{cases} 1, & \text{if } \mathbf{w}^T\mathbf{x} + b \geq 0 \\ 0, & \text{otherwise} \end{cases} y={1,0,if wTx+b≥0otherwise
✅ 所以我们得出关键结论:
b = − θ \boxed{b = -\theta} b=−θ
即:偏置 = 负的阈值
阈值 θ θ θ:输入需要超过的"门槛"
偏置 b b b:用于平移决策边界
4.2如何直观理解"偏置"?
偏置 b b b 的作用是调节神经元的激活难度,你可以把它看作一个"灵活性开关"或"决策门槛控制器"。
生活例子:是否去参加聚会?
假设你根据两个因素做决定:
- x 1 = 1 x_1 = 1 x1=1:天气好
- x 2 = 1 x_2 = 1 x2=1:好朋友去
对应权重:
- w 1 = 0.6 w_1 = 0.6 w1=0.6:比较在意天气
- w 2 = 0.8 w_2 = 0.8 w2=0.8:很在意朋友是否去
情况 1:无偏置( b = 0 b = 0 b=0)
z = 0.6 x 1 + 0.8 x 2 z = 0.6x_1 + 0.8x_2 z=0.6x1+0.8x2
只要有一点理由就可能触发 → 容易去(低门槛)
情况 2:加上负偏置( b = − 1.5 b = -1.5 b=−1.5)
z = 0.6 x 1 + 0.8 x 2 − 1.5 z = 0.6x_1 + 0.8x_2 - 1.5 z=0.6x1+0.8x2−1.5
即使天气好但朋友不去: 0.6 ( 1 ) + 0.8 ( 0 ) − 1.5 = − 0.9 < 0 0.6(1) + 0.8(0) - 1.5 = -0.9 < 0 0.6(1)+0.8(0)−1.5=−0.9<0 → 不去
👉 偏置越大(正值),越容易激活;偏置越小(负值),越难激活。
4.3几何意义:偏置控制决策边界的平移
在二维空间中,感知机的决策边界是一条直线:
w 1 x 1 + w 2 x 2 + b = 0 w_1 x_1 + w_2 x_2 + b = 0 w1x1+w2x2+b=0
- 权重 w \mathbf{w} w 决定这条线的 方向(法向量)
- 偏置 b b b 决定这条线离原点的 距离和平移方向
举例
- b = 0 b=0 b=0:决策边界经过原点
- b > 0 b>0 b>0 :边界向输入空间负方向移动 → 更容易输出 1
- b < 0 b<0 b<0 :边界远离正区域 → 更难激活
✅ 类比考试及格线:
- 把及格线从 60 分降到 50 分 → 更多人通过(相当于 b b b 增大)
- 提高到 70 分 → 更严格(相当于 b b b 减小)