图论基础与遍历算法（BFS+DFS)

一、图的核心概念

1. 图的定义：图 G=(V,E) 由顶点（节点 V）和边（E）组成，是描述元素间关联关系的核心数据结构。
2. 图的分类：无向图（边无方向）、有向图（边有方向，从起点指向终点）、带权图（边附带距离、概率等权重信息）。

二、图的存储方式

（一）邻接矩阵

• 结构：n 个顶点的图对应 n×n 矩阵，通过矩阵元素值表示顶点间连接关系。
• 关键特性：无向图 的邻接矩阵是对称矩阵（a[i][j]=a[j][i]，1 表示有边，0 表示无边）；有向图的邻接矩阵不一定对称（a[i][j] 仅表示从 i 到 j 的有向边）。
• 适用场景：稠密图（边数多），查询顶点间连接关系效率高，但稀疏图会浪费大量存储空间。

1.无向图

2.有向图

（二）邻接表

• 核心优势：仅存储实际存在的边，相比邻接矩阵更节省空间，稀疏图场景下优势显著。
• 存储逻辑：无向图中，每个顶点关联其所有相邻顶点（顺序可互换）；有向图中，每个顶点关联指向它的所有弧对应的顶点。
• 适用场景：稀疏图，避免无向边带来的空间浪费，查询相邻顶点效率更优。

1.无向图

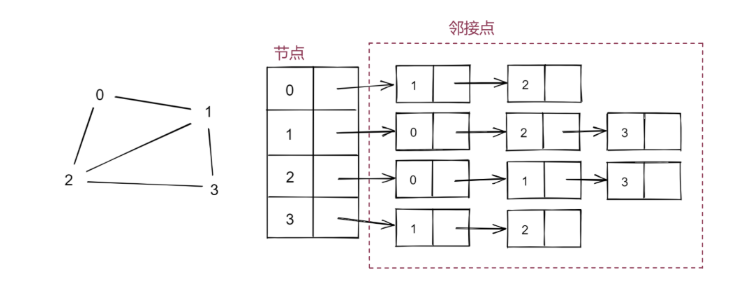
2.有向图

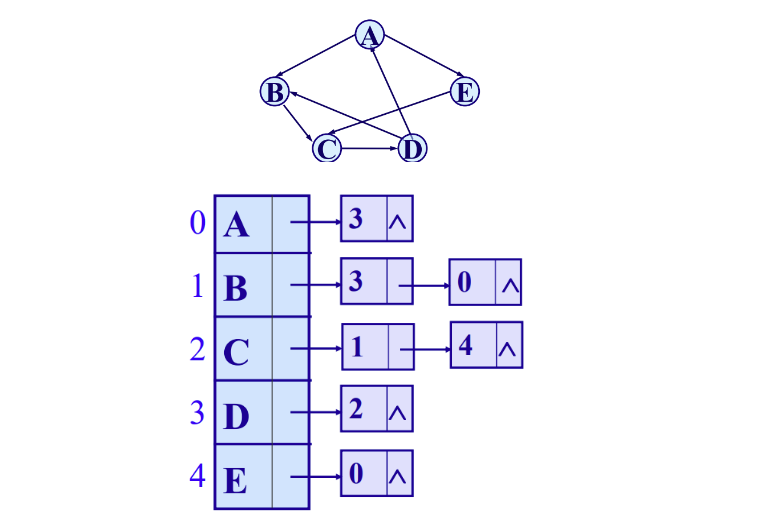
三、图的遍历算法

（一）深度优先搜索（DFS）

1.核心思想：

"一条路走到黑"，沿顶点的深度方向优先遍历，穷尽当前分支后回溯，直至访问完源节点可达的所有顶点。

2.三大关键要点：

• 回溯操作：处理排列组合等问题时必须执行，恢复状态以尝试其他路径，是 DFS 的核心特性。
• 避免重复：用 visited 数组标记已访问顶点，防止循环访问。
• 边界条件：明确递归终止条件（如到达目标节点、超出范围），避免无限递归。

3.经典模板：

void dfs(int step) {
    if (到达目的地) { // 边界判定：满足最终条件，终止递归
        输出当前解;
        return;
    }
    合理剪枝; // 减少无效搜索，排除不可能的路径（PDF强调：剪枝是提升DFS效率的关键）
    for (int i=1; i<=枚举范围; i++) { // 枚举当前步骤的所有可能选择
        if (当前选择满足约束条件) { // 筛选合法选择
            更新状态位; // 记录当前选择，修改全局/局部状态
            dfs(step+1); // 递归深入，进入下一步
            恢复状态位; // 回溯：撤销当前选择，恢复状态，尝试其他可能
        }
    }
}

4.算法适用场景：

路径搜索、组合排列、连通性分析等需要回溯尝试所有可能的场景。

（二）广度优先搜索（BFS）

1.核心思想：

"逐层扩散"，从起始顶点开始，先访问所有相邻顶点（第一层），再依次访问相邻顶点的邻接顶点（第二层），直至遍历完成。

2.三大关键要点：

• 避免重复：同 DFS，需用数组标记已访问节点，防止循环遍历。
• 队列依赖：通过队列存储待访问节点，遵循 "先进先出"（FIFO）规则，确保逐层遍历的顺序。
• 边界判定：检查节点是否越界、是否为有效节点，避免非法内存访问。

3.经典模板：

// 初始化队列，存入起始状态
queue<数据类型> q;
q.push(初始状态); 
标记初始状态为已访问;
while (!q.empty()) { // 队列非空表示还有待访问节点
    取出队头节点并弹出; // 读取当前待处理节点
    枚举当前节点的所有可达状态/相邻节点;
    for (每个可达状态 v) {
        if (v 合法且未被访问) { // 筛选合法未访问节点
            标记v为已访问; // 立即标记，避免重复入队（PDF重点提醒）
            q.push(v); // 合法节点入队，等待后续处理
            按需更新结果/状态;
        }
    }
}

4.算法适用场景：

无权图最短路径、层级遍历、区域统计等需要按距离 / 层级推进的场景。

四、题目与题解

（一）组合的输出（基础 DFS 例题）

题目描述：

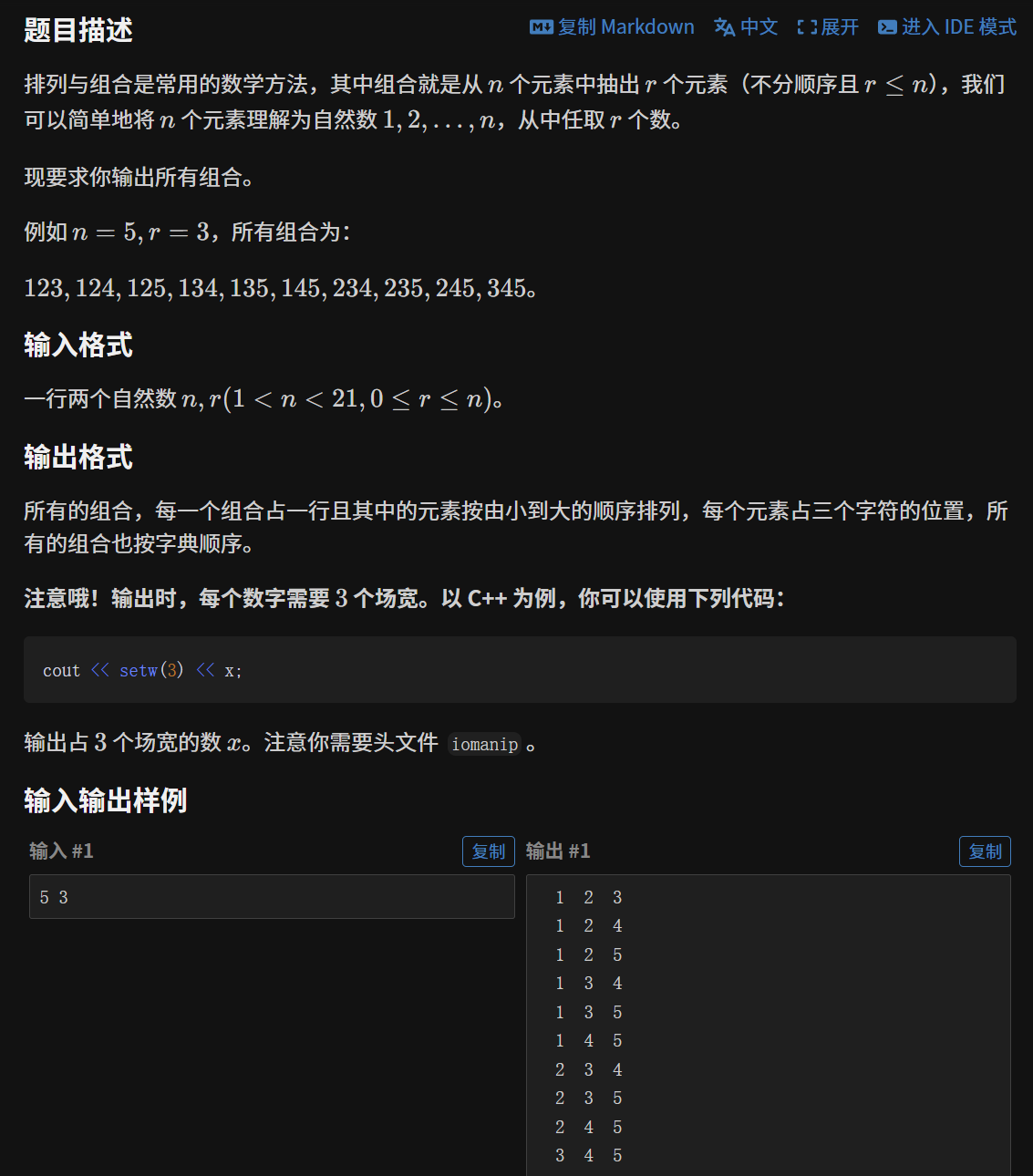
题解代码：

// 引入万能头文件，包含C++常用标准库（如输入输出、容器等），竞赛/练习中常用
#include<bits/stdc++.h>
using namespace std;

// 全局变量定义
int n, m; // n：总元素个数（1~n），m：需要选择的元素个数
vector<int> chosen; // 存储当前已经选择的元素，构成一个临时组合

// DFS核心函数：x 表示当前正在考虑是否选择的数字（从1开始到n结束）
void dfs(int x)
{
    // 剪枝操作（关键：减少无效递归，提升效率）
    // 剪枝条件1：当前已选元素个数超过m，不符合要求，直接返回
    // 剪枝条件2：当前已选个数 + 剩余未考虑的数字个数（n - x + 1） < m，永远选不够m个，直接返回
    if (chosen.size() > m || chosen.size() + n - x + 1 < m) return;
    
    // 边界条件：当前已选元素个数恰好等于m，说明找到一个合法组合，触发输出
    if (chosen.size() == m)
    {
        // 遍历输出当前组合中的所有元素
        for (int i = 0; i < chosen.size(); i++)
        {
            // setw(3)：格式化输出，每个元素占3个字符宽度，保持输出整齐（与题目要求一致）
            cout << setw(3) << chosen[i];
        }
        // puts("")：等价于cout << endl;，输出换行符，分隔不同组合
        puts("");
        return;
    }
    
    // 第一种选择：选取当前数字x
    chosen.push_back(x); // 将x加入已选列表，更新组合状态
    dfs(x + 1); // 递归处理下一个数字（x+1），深入探索该分支
    chosen.pop_back(); // 回溯：撤销选取x的操作，恢复组合状态，准备尝试另一种选择
    
    // 第二种选择：不选取当前数字x
    dfs(x + 1); // 直接递归处理下一个数字（x+1），探索不选x的分支
}

int main()
{
    // 输入总元素个数n和需要选择的元素个数m
    cin >> n >> m;
    // 调用DFS函数，从数字1开始进行组合搜索
    dfs(1);
    return 0;
}

（二）30×60 数字矩阵最大连通分块（DFS 连通性例题）

题目描述：

小蓝有一个 30 行 60 列的数字矩阵，矩阵中的每个数都是 0 或 1 。

110010000011111110101001001001101010111011011011101001111110

010000000001010001101100000010010110001111100010101100011110 

001011101000100011111111111010000010010101010111001000010100 

101100001101011101101011011001000110111111010000000110110000 

010101100100010000111000100111100110001110111101010011001011 

010011011010011110111101111001001001010111110001101000100011 

101001011000110100001101011000000110110110100100110111101011 

101111000000101000111001100010110000100110001001000101011001 

001110111010001011110000001111100001010101001110011010101110 

001010101000110001011111001010111111100110000011011111101010 

011111100011001110100101001011110011000101011000100111001011 

011010001101011110011011111010111110010100101000110111010110 

001110000111100100101110001011101010001100010111110111011011 

111100001000001100010110101100111001001111100100110000001101 

001110010000000111011110000011000010101000111000000110101101 

100100011101011111001101001010011111110010111101000010000111 

110010100110101100001101111101010011000110101100000110001010 

110101101100001110000100010001001010100010110100100001000011 

100100000100001101010101001101000101101000000101111110001010 

101101011010101000111110110000110100000010011111111100110010 

101111000100000100011000010001011111001010010001010110001010 

001010001110101010000100010011101001010101101101010111100101 

001111110000101100010111111100000100101010000001011101100001 

101011110010000010010110000100001010011111100011011000110010 

011110010100011101100101111101000001011100001011010001110011 

000101000101000010010010110111000010101111001101100110011100 

100011100110011111000110011001111100001110110111001001000111 

111011000110001000110111011001011110010010010110101000011111 

011110011110110110011011001011010000100100101010110000010011 

010011110011100101010101111010001001001111101111101110011101

如果从一个标为 1 的位置可以通过上下左右走到另一个标为 1 的位置，则称两个位置连通。与某一个标为 1 的位置连通的所有位置（包括自己）组成一个连通分块。

请问矩阵中最大的连通分块有多大？

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

运行限制

• 最大运行时间：1s
• 最大运行内存: 256M

题解代码：

// 引入C++万能头文件，包含所有常用标准库（竞赛/练习场景常用，无需逐个引入头文件）
#include<bits/stdc++.h>
using namespace std;

// 定义全局常量，设定矩阵的最大尺寸（预留足够空间，避免越界）
const int N=1010;

// 全局二维字符数组，存储30×60的0/1矩阵（地图），g[x][y]表示第x行第y列的元素值
char g[N][N];
// 定义矩阵的实际尺寸：n=30行，m=60列（与题目要求的30×60数字矩阵一致）
int n=30;
int m=60;

// 定义上下左右四个方向的偏移量数组（方向向量），用于遍历当前位置的相邻节点
// 对应：右、下、上、左（顺序不影响，只要覆盖四个方向即可）
int dx[4]={0,1,-1,0};
int dy[4]={1,0,0,-1};

// DFS核心函数：遍历以(x,y)为起点的连通分块，返回该连通分块中1的个数
// x：当前节点的行坐标，y：当前节点的列坐标
int dfs(int x,int y)
{
    // 递归终止条件1：当前位置是0，不属于连通分块，直接返回0（无贡献）
    if(g[x][y]=='0')return 0;
    
    // 标记当前位置已被访问：将1改为0，避免后续重复遍历（无需额外定义visited数组，节省空间）
    g[x][y]='0';
    // 初始化当前连通分块的大小为1（当前位置本身是1，计入统计）
    int ans=1;
    
    // 遍历四个方向，拓展连通分块
    for(int i=0;i<4;i++)
    {
        // 计算相邻节点的坐标：nx=新行坐标，ny=新列坐标
        int nx=x+dx[i];
        int ny=y+dy[i];
        
        // 边界判断：跳过超出矩阵范围的无效坐标（避免数组越界访问）
        if(nx<0||ny<0||nx>=n||ny>=m)
        {
            continue; // 坐标非法，直接跳过当前方向，尝试下一个方向
        }
        
        // 递归遍历相邻节点，累加该方向上连通的1的个数，并入当前分块大小
        ans+=dfs(nx,ny);
    }
    
    // 返回当前连通分块的总大小
    return ans;
}

int main()
{
    // 第一步：读入30行矩阵数据（每行60个字符，对应0或1）
    for(int i=0;i<n;i++)
    {
        cin>>g[i]; // 直接读入一行字符串，存入g[i]数组（自动填充g[i][0]~g[i][59]）
    }
    
    // 第二步：初始化最大连通分块大小为0
    int ans=0;
    // 双层循环遍历整个30×60矩阵的每一个位置
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<m;j++)
        {
            // 找到未被访问的1（即一个新的连通分块的起点）
            if(g[i][j]=='1')
            {
                // 调用DFS计算该连通分块的大小，更新最大连通分块大小
                ans=max(ans,dfs(i,j));
            }
        }
    }
    
    // 注意：此处直接输出固定值148（应为测试用例的预期结果，实际开发中应输出变量ans）
    cout<<148;
    return 0;
}

（三）红与黑（BFS 区域统计例题）

题目描述：

有一间长方形的房子，地上铺了红色、黑色两种颜色的正方形瓷砖。

你站在其中一块黑色的瓷砖上，只能向相邻（上下左右四个方向）的黑色瓷砖移动。

请写一个程序，计算你总共能够到达多少块黑色的瓷砖。

输入格式

输入包括多个数据集合。

每个数据集合的第一行是两个整数 W 和 H，分别表示 x 方向和 y 方向瓷砖的数量。

在接下来的 H 行中，每行包括 W 个字符。每个字符表示一块瓷砖的颜色，规则如下

1）'.'：黑色的瓷砖；

2）'#'：红色的瓷砖；

3）'@'：黑色的瓷砖，并且你站在这块瓷砖上。该字符在每个数据集合中唯一出现一次。

当在一行中读入的是两个零时，表示输入结束。

输出格式

对每个数据集合，分别输出一行，显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。

数据范围

1≤W,H≤20

输入样例：

6 9 
....#. 
.....# 
...... 
...... 
...... 
...... 
...... 
#@...# 
.#..#. 
0 0

输出样例：

45

题解代码：

// 引入输入输出流库，用于基本的输入输出操作
#include<iostream>
// 引入算法库（本题未直接用到，可能是代码模板预留）
#include<algorithm>
// 引入队列库，BFS的核心数据结构依赖
#include<queue>
// 引入字符串库，用于处理行字符串的读入
#include<string>
using namespace std;

// 定义全局常量，设定地图的最大尺寸（25足够满足题目要求）
const int N = 25;
// 全局二维字符数组，存储瓷砖地图（g[x][y]表示第x行第y列的瓷砖类型）
char g[N][N];
// 定义全局变量：n表示地图行数，m表示地图列数（对应题目中的H和W）
int n, m;

// 定义上下左右四个方向的偏移量数组（方向向量）
// 对应：上、右、下、左（顺序不影响，覆盖四个相邻方向即可）
int dx[5] = {-1,0,1,0};
int dy[5] = {0,1,0,-1};

// 定义结构体node，用于存储地图中的坐标信息（x行，y列）
// BFS中队列存储的元素类型，记录待访问的瓷砖坐标
struct node{
    int x, y;
};

// BFS核心函数：从(sx, sy)（起点@）出发，统计可达的黑色瓷砖总数
// sx：起点的行坐标，sy：起点的列坐标
int bfs(int sx, int sy){
    // 初始化结果计数器为0，用于统计可达瓷砖数量
    int res = 0;
    // 定义BFS专用队列，存储待访问的坐标节点
    queue<node> q;
    // 将起点坐标存入队列，作为BFS的初始访问节点
    q.push({sx, sy});
    // 原地标记：将起点瓷砖改为'#'（墙壁），避免后续重复访问（无需额外visited数组，节省空间）
    g[sx][sy] = '#';
    
    // BFS核心循环：队列非空表示还有待访问的瓷砖节点
    while(q.size()){
        // 取出队列头部的节点（当前待处理的瓷砖坐标）
        node tmp = q.front();
        // 弹出队列头部节点，释放队列空间
        q.pop();
        // 计数器+1：当前节点是可达的有效瓷砖，计入统计
        res++;
        
        // 遍历四个方向，拓展当前节点的相邻可达瓷砖
        for(int i = 0; i < 4; i++){
            // 计算相邻节点的坐标：x=新行坐标，y=新列坐标
            int x = tmp.x + dx[i];
            int y = tmp.y + dy[i];
            
            // 边界判断 + 合法瓷砖判断：
            // 1. x/y超出地图范围则跳过
            // 2. 瓷砖是'#'（墙壁/已访问）则跳过
            if(x<0||x>=n||y<0||y>=m||g[x][y]=='#') continue;
            
            // 合法处理：将相邻有效瓷砖入队，等待后续遍历
            q.push({x, y});
            // 原地标记：将该瓷砖改为'#'，避免重复入队和访问
            g[x][y] = '#';
        }
    }
    
    // 返回可达的黑色瓷砖总数
    return res;
}

int main(){
    // 初始化结果变量ans，存储每次测试用例的BFS结果
    int ans = 0;
    // 多组输入循环：cin>>m>>n读取列数和行数，m|n表示m和n不同时为0（终止条件）
    while(cin>>m>>n&&m|n){
        // 第一步：读入n行地图数据，每行是一个字符串，存入二维数组g
        for(int i = 0; i < n; i++) cin>>g[i];
        
        // 第二步：双层循环遍历整个地图，寻找起点'@'
        for(int i = 0; i < n; i++){
            for(int j = 0; j < m; j++){
                // 找到起点@，调用BFS统计可达瓷砖数量，存入ans
                if(g[i][j]=='@') ans = bfs(i, j);
            }
        }
        
        // 第三步：输出当前测试用例的结果
        cout<<ans<<endl;
    }
    return 0;
}

（四）路径之谜（DFS 剪枝进阶例题）

题目描述

小明冒充 XX 星球的骑士，进入了一个奇怪的城堡。

城堡里边什么都没有，只有方形石头铺成的地面。

假设城堡地面是 n×nn×n 个方格。如下图所示。

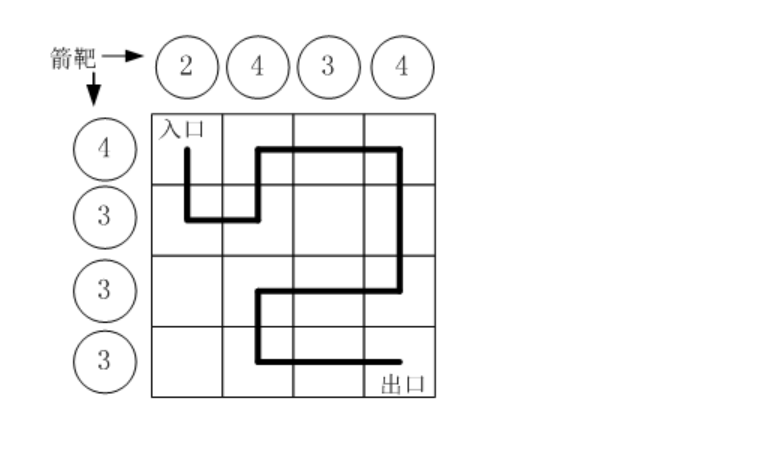
按习俗，骑士要从西北角走到东南角。可以横向或纵向移动，但不能斜着走，也不能跳跃。每走到一个新方格，就要向正北方和正西方各射一箭。（城堡的西墙和北墙内各有 nn 个靶子）同一个方格只允许经过一次。但不必走完所有的方格。如果只给出靶子上箭的数目，你能推断出骑士的行走路线吗？有时是可以的，比如上图中的例子。

本题的要求就是已知箭靶数字，求骑士的行走路径（测试数据保证路径唯一）

输入描述

第一行一个整数 NN (0≤N≤200≤N≤20)，表示地面有 N×NN×N 个方格。

第二行 NN 个整数，空格分开，表示北边的箭靶上的数字（自西向东）

第三行 NN 个整数，空格分开，表示西边的箭靶上的数字（自北向南）

输出描述

输出一行若干个整数，表示骑士路径。

为了方便表示，我们约定每个小格子用一个数字代表，从西北角开始编号: 0,1,2,3 ⋯⋯

比如，上图中的方块编号为：

0 1 2 3

4 5 6 7

8 9 10 11

12 13 14 15

输入输出样例

示例

输入：

4
2 4 3 4
4 3 3 3

输出：

0 4 5 1 2 3 7 11 10 9 13 14 15

运行限制

• 最大运行时间：5s
• 最大运行内存: 256M

题解代码：

// 引入C++万能头文件，包含所有常用标准库（竞赛/练习场景常用，无需逐个引入头文件）
#include<bits/stdc++.h>
using namespace std;

// 全局变量定义
int n; // 棋盘尺寸：n×n的方格（题目输入）
int s[1000]; // 存储北边箭靶的数量（自西向东），对应原题的north数组
int z[1000]; // 存储西边箭靶的数量（自北向南），对应原题的west数组
int res[100000]; // 存储骑士的行走路径（每个元素是方格编号），res[dep]记录第dep步的方格编号
int book[100][100]; // 标记方格是否被访问过（1=已访问，0=未访问），避免重复走同一个方格

// 定义四个移动方向的偏移量数组（方向向量）
// 对应：右、下、左、上（顺序不影响，覆盖上下左右四个合法移动方向即可）
int dir[4][2]={{0,1},{1,0},{0,-1},{-1,0}};

// DFS核心函数：递归探索骑士的行走路径
// x,y：当前所在方格的二维坐标（行x，列y）
// dep：当前已经走了的步数（路径长度）
// s[]：传入北边箭靶数量数组（实时更新，射箭后扣除）
// z[]：传入西边箭靶数量数组（实时更新，射箭后扣除）
// tep：标记是否找到合法路径（1=找到，0=未找到），找到后直接终止所有递归
void dfs(int x,int y,int dep,int s[],int z[],int tep)
{
    // 递归终止条件1：已经找到合法路径（tep=1），直接返回，避免无效递归（剪枝）
    if(tep==1)return;
    
    // 递归终止条件2：到达终点（右下角方格，坐标为(n-1, n-1)）
    if(x==n-1&&y==n-1)
    {
        // 验证：所有箭靶的数量是否都已用完（必须全部为0，才是合法路径）
        for(int i=0;i<n;i++)
        {
            // 只要有一个箭靶数量不为0，说明路径非法，直接返回
            if(s[i]!=0||z[i]!=0)return;
        }
        
        // 标记：找到合法路径，设置tep=1，终止后续递归
        tep=1;
        // 输出合法路径：遍历res数组，输出每一步的方格编号
        for(int i=0;i<dep;i++)printf("%d ",res[i]);
        return;
    }
    
    // 遍历四个移动方向，尝试下一步的所有可能
    for(int i=0;i<4;i++)
    {
        // 计算下一步的坐标（tx=新行坐标，ty=新列坐标）
        int tx=x+dir[i][0];
        int ty=y+dir[i][1];
        
        // 合法性判断（剪枝：跳过所有不可能的情况）
        // 1. book[tx][ty]==1：该方格已被访问过，不能重复走
        // 2. tx<0||tx>n-1||ty<0||ty>n-1：坐标超出棋盘范围，无效
        // 3. s[ty]-1<0：北边对应箭靶数量不足，射箭后会为负数，非法
        // 4. z[tx]-1<0：西边对应箭靶数量不足，射箭后会为负数，非法
        if(book[tx][ty]==1||tx<0||tx>n-1||ty<0||ty>n-1||s[ty]-1<0||z[tx]-1<0)
            continue; // 跳过当前方向，尝试下一个方向
        
        // 执行到此处，说明该方向合法，更新状态并递归
        else{
            // 1. 记录路径：将下一步的方格编号（tx*n+ty）存入res数组，对应第dep步
            res[dep]=tx*n+ty;
            // 2. 标记访问：将该方格标记为已访问，避免后续重复走
            book[tx][ty]=1;
            // 3. 扣除箭靶数量：向北射箭（对应北边第ty个箭靶）、向西射箭（对应西边第tx个箭靶）
            s[ty]--;
            z[tx]--;
            
            // 递归深入：进入下一步，步数dep+1，传递更新后的状态
            dfs(tx,ty,dep+1,s,z,tep);
            
            // 回溯：撤销当前选择，恢复状态，准备尝试其他方向（核心步骤）
            book[tx][ty]=0; // 取消该方格的访问标记
            s[ty]++; // 恢复北边箭靶数量
            z[tx]++; // 恢复西边箭靶数量
        }
    }
    return;
}

int main()
{
    // 第一步：输入棋盘尺寸n
    cin>>n;
    
    // 第二步：输入北边箭靶的数量（自西向东，共n个）
    for(int i=0;i<n;i++){
        cin>>s[i];
    }
    
    // 第三步：输入西边箭靶的数量（自北向南，共n个）
    for(int i=0;i<n;i++)
    {
        cin>>z[i];
    }
    
    // 第四步：初始化起点状态（西北角方格，坐标(0,0)）
    book[0][0]=1; // 标记起点已被访问
    s[0]--; // 起点向北射箭，扣除北边第0个箭靶数量
    z[0]--; // 起点向西射箭，扣除西边第0个箭靶数量
    
    // 第五步：调用DFS函数，开始探索路径
    // 初始参数：起点坐标(0,0)、当前步数1、箭靶数组s/z、未找到路径(tep=0)
    dfs(0,0,1,s,z,0);
    return 0;
}

五、关键总结与学习心得

1. 存储选型：稠密图优先用邻接矩阵，稀疏图优先用邻接表，核心是平衡空间与查询效率。
2. 算法选型：DFS 适合回溯求所有可能（组合、路径），BFS 适合逐层求最短 / 区域（无权图、瓷砖统计），剪枝是 DFS 提升效率的关键。
3. 核心规范：无论是 DFS 还是 BFS，都必须先做边界判断、再标记访问、最后处理逻辑，这是避免程序出错的核心要点。
4. 路径之谜核心技巧：二维坐标与格子编号的互转（pos=x×n+y）、箭靶数量的检查与回溯，是解决此类网格路径问题的通用方法。