【LeetCode经典题解】搞定二叉树最近公共祖先：递归法+栈存路径法，附代码实现

🎁个人主页：User_芊芊君子

🎉欢迎大家点赞👍评论📝收藏⭐文章

🔍系列专栏：Java.数据结构

【前言】

二叉树的最近公共祖先是数据结构中的经典问题，无论是算法面试还是实际开发都高频出现。本文将从问题本身出发，拆解递归法与栈存路径法两种核心思路的逻辑步骤，并附上完整代码实现，帮你快速掌握这一考点。

文章目录：

一、二叉树的最近共同祖先
二、思路分析
三、代码展示
- 方法一：递归法
- 方法二：栈存路径法
四、总结

一、二叉树的最近共同祖先

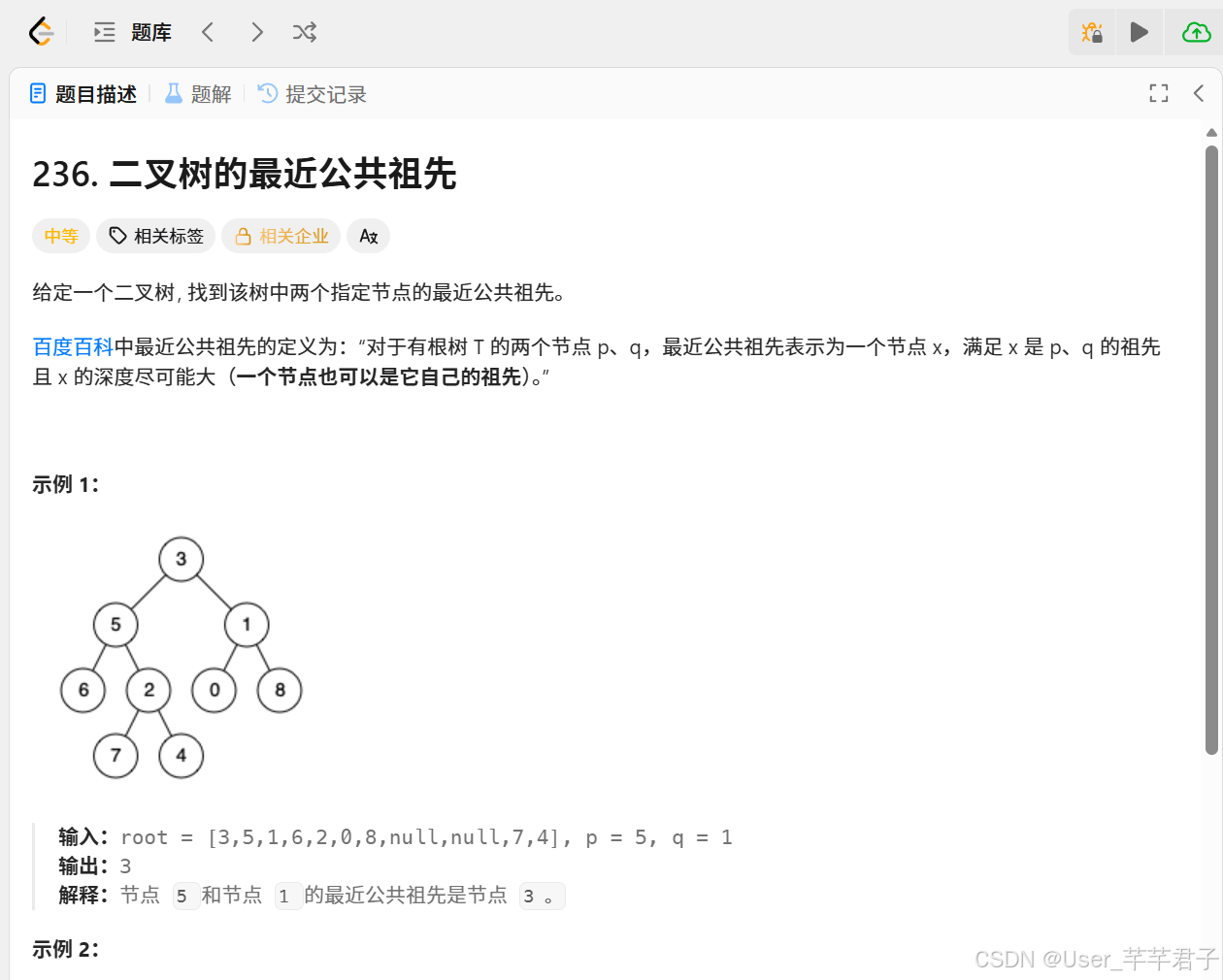
二、思路分析

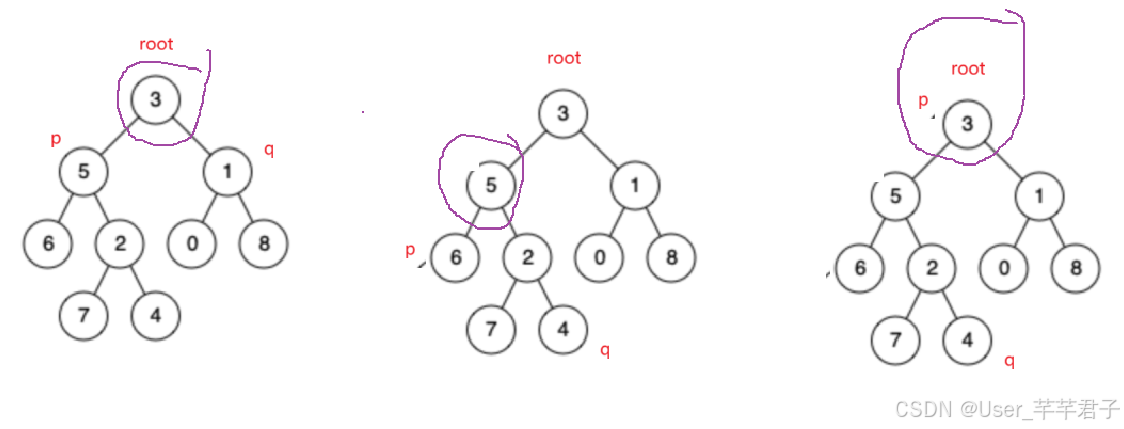
方法一：递归法

判空

如果根节点为空，直接返回null
如果当前节点是p或者q，那么这个节点就是最近公共祖先

递归

分别遍历当前节点的左子树和右子树，找到p和q的最近公共祖先，存于TreeNode leftRet或者TreeNode rightRet

结果

如果左右子树都找到，那么当前节点就是p和q的最近公共祖先
如果左子树找到，那就返回左子树的结果；
如果右子树找到，那就返回右子树的结果；

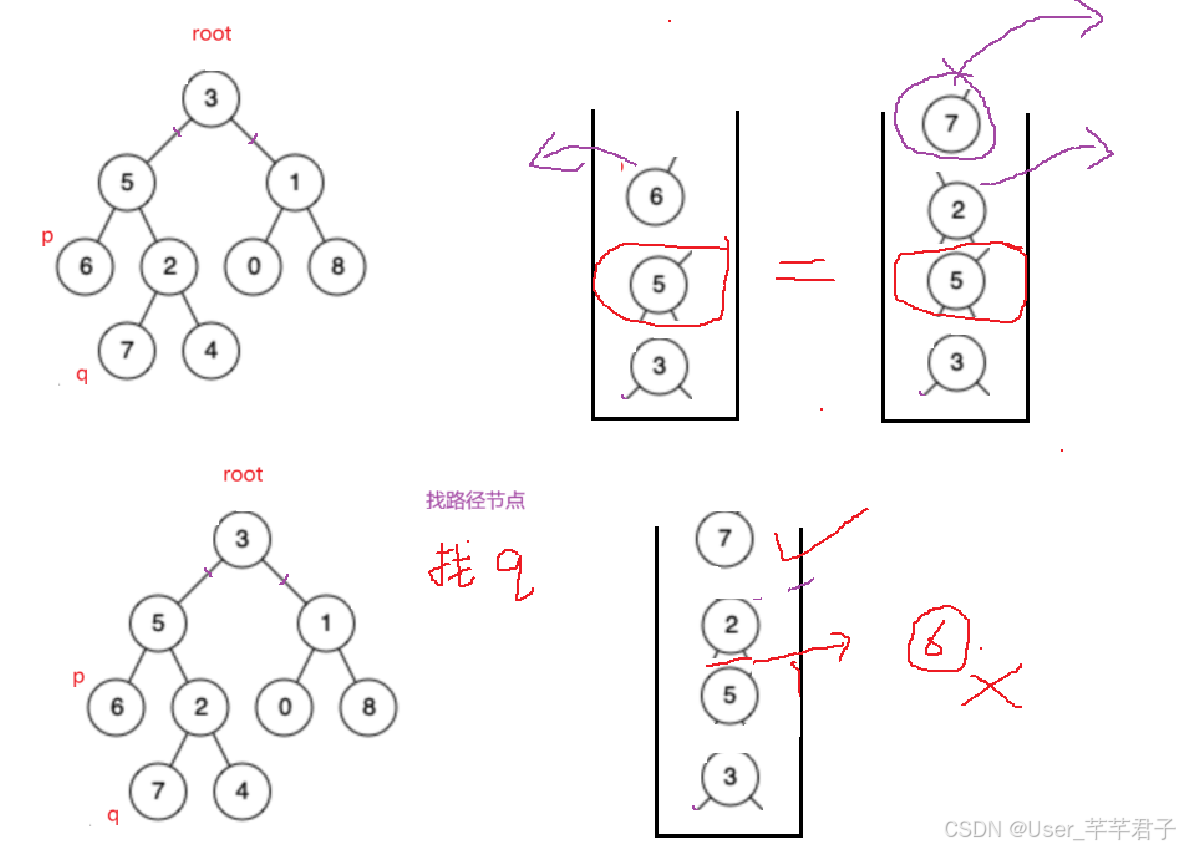
方法二：栈存路径法

获取路径

通过深度优先搜索，分别找到从根节点到p和q的路径中所有节点，并分别存入两个栈中

对齐栈长度

比较两个栈中元素长度，将较长的栈中元素弹出，然后比较两个栈中的下一深度元素是否相等

找公共祖先

同时弹出两个栈中不相等的栈顶元素，第一个相同的节点就是最近公共祖先

三、代码展示

方法一：递归法

java 复制代码

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        //当前节点为空，直接返回null
        if(root == null){
            return null;
        }
        //当前节点是p或者q，返回当前节点（祖先）
        if(root == p || root == q){
            return root;
        }
        //递归探索左子树，找到p和q的最近祖先
        TreeNode leftRet = lowestCommonAncestor(root.left, p, q);
        //递归探索右子树，找到p和q的最近祖先
        TreeNode rightRet = lowestCommonAncestor(root.right, p, q);
        //左子树和右子树都找到
        if(leftRet != null && rightRet != null){
            return root;
            //左子树找到
        }else if(leftRet != null){
            return leftRet;
        }else{//右子树找到
            return rightRet;
        }
    }

方法二：栈存路径法

java 复制代码

public boolean getPath(TreeNode root, TreeNode node, Stack<TreeNode> stack) {
        if(root == null){
            return false;
        }
        //将当前节点压入路径
        stack.push(root);
        //找到目标节点
        if(root == node){
            return true;
        }
        //递归搜索左子树
        boolean flg = getPath(root.left,node,stack);
        if(flg){
            return true;
        }
        //递归搜索右子树
        flg = getPath(root.right,node,stack);
        if(flg){
            return true;
        }
        //左右子树都没找到，弹出当前节点
        stack.pop();
        return false;
    }
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q){
        if(root == null){
            return null;
        }
        //找到跟到p和q的路径
        Stack<TreeNode> stackp = new Stack<>();
        Stack<TreeNode> stackq = new Stack<>();
        getPath(root,p,stackp);
        getPath(root,q,stackq);
        //对齐两个栈长度
        int sizep = stackp.size();
        int sizeq = stackq.size();
        int size = sizep-sizeq;
        if(size>0){
            //stacp更长，弹出多余元素
            while (size != 0){
                stackp.pop();
                size--;
            }
        }else {
            ////stacq更长，弹出多余元素
            size = sizeq-sizep;
            while (size != 0){
                stackq.pop();
                size--;
            }
        }
        //此时两个栈大小一样，//同时弹出栈顶，找到相同的
        while (!stackp.isEmpty()&&!stackq.isEmpty()){
            if(stackp.peek().equals(stackq.peek())){
                return stackp.peek();
            }
            stackp.pop();
            stackq.pop();
        }
        return null;
    }

四、总结

通过递归法的"自底向上"回溯，以及栈存路径法的"路径对比"思路，我们可以高效求解二叉树的最近公共祖先问题------前者利用递归特性简化代码，后者通过显式路径存储更直观易懂。结合本文的思路分析与代码示例，你可以根据场景灵活选择解法，轻松应对这类二叉树算法题。