在学术研究与统计分析中,置信区间(Confidence Interval, CI) 是描述参数估计不确定性与统计可靠性的核心指标。相比标准差(SD)与标准误(SEM),CI 直接对应统计推断问题,更能反映估计结果的可信范围,因此已成为多数期刊论文中更推荐的误差表达形式。
CI 曲线通过将"均值趋势线"与"连续置信区间带"进行融合,可在同一图表中同时呈现:
- 数据变化趋势(Trend)
- 估计不确定性(Uncertainty)
- 统计推断可靠性(Inference reliability)
该形式在时间序列分析、剂量--反应关系、连续变量建模、多组处理对比等科研场景中被广泛使用。
一、置信区间(CI)的核心概念与计算方法
1. 核心定义
置信区间是指在给定置信水平(科研中通常为 95% )下,对总体参数(如均值)真实取值范围的区间估计。
其统计含义为:
在重复进行大量相同实验的前提下,约 95% 的区间能够覆盖总体真实参数。
与 SD(描述样本离散程度)和 SEM(描述均值估计误差)不同,CI 更贴合统计推断语境,因此在论文结果展示中具有更明确的统计解释。
2. 95% CI 的通用计算公式
针对样本均值,其 95% 置信区间为:
其中:
-
:样本均值
-
:t 分布临界值(自由度
)
-
当样本量较大(n \\ge 30)且近似正态分布时,可采用正态近似:
3. 科研计算要点
- 默认置信水平为 95% CI,无需在图中反复说明
- 小样本(n < 30)必须使用 t 分布
- CI 上下限需与对应均值一一对应
- 不可将"整组 CI"错误应用于所有数据点
二、基础 CI 曲线:趋势线 + 连续置信区间带
基础 CI 曲线由两部分构成:
- 均值趋势线(反映整体变化趋势)
- 连续 CI 区间带(反映估计不确定性)
科研级绘图要求 CI 区间带透明、无轮廓,并且不干扰趋势线的判读。
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
# 加载科研标准化样式
def set_scientific_plot_style():
plt.rcParams.update({
'font.family': 'serif',
'font.serif': ['Times New Roman', 'DejaVu Serif'],
'font.sans-serif': ['SimHei', 'Arial Unicode MS'],
'axes.unicode_minus': False,
'font.size': 10,
'axes.titlesize': 12,
'axes.labelsize': 10,
'xtick.labelsize': 9,
'ytick.labelsize': 9,
'legend.fontsize': 9,
'axes.linewidth': 0.8,
'lines.linewidth': 1.8,
'lines.markersize': 4,
'xtick.major.width': 0.8,
'ytick.major.width': 0.8,
'xtick.minor.visible': True,
'ytick.minor.visible': True,
'grid.alpha': 0.2,
'grid.linestyle': '--',
'grid.linewidth': 0.6,
'savefig.dpi': 300,
'savefig.facecolor': 'white'
})
set_scientific_plot_style()
# ===================== 1. 模拟数据并计算95%CI =====================
np.random.seed(42)
x = np.linspace(0, 10, 20)
n = 15
y_mean = 2.5 * np.sin(x) + 5
y_samples = y_mean[:, np.newaxis] + np.random.normal(0, 1.2, (20, n))
y_means = np.mean(y_samples, axis=1)
y_sd = np.std(y_samples, axis=1, ddof=1)
y_sem = y_sd / np.sqrt(n)
t_crit = stats.t.ppf(0.975, df=n-1)
ci_lower = y_means - t_crit * y_sem
ci_upper = y_means + t_crit * y_sem
# ===================== 2. 绘制CI曲线 =====================
fig, ax = plt.subplots(figsize=(3.54, 2.36))
ax.fill_between(x, ci_lower, ci_upper,
color='#1f77b4', alpha=0.3, label='95% CI')
ax.plot(x, y_means,
color='#1f77b4', linewidth=2.0, label='Mean Value')
ax.set_title('Basic 95% Confidence Interval (CI) Curve')
ax.set_xlabel('Independent Variable (X)')
ax.set_ylabel('Dependent Variable (Y)')
ax.legend(frameon=False)
ax.grid(axis='y', alpha=0.2)
ax.set_ylim(0, 10)
plt.show()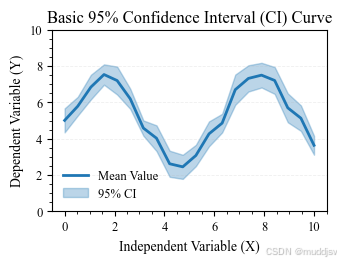
可视化要点
- CI 区间带先绘制、趋势线后绘制
- 透明度建议 0.2--0.4
- CI 区间带不设置边框(edgecolor)
三、多组 CI 曲线对比:分组趋势与可靠性分析
在科研实践中,常需要同时比较多组数据的变化趋势及其统计可靠性(如对照组与多个处理组)。此时应对每一组数据独立计算 CI,并以统一样式进行绘制。
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
set_scientific_plot_style()
np.random.seed(42)
x = np.linspace(0, 10, 20)
n = 12
# ===================== 三组数据 =====================
y_ctrl = (
2.0 * np.sin(x)[:, np.newaxis] + 4
+ np.random.normal(0, 1.0, (20, n))
)
y_a = (
2.5 * np.sin(x)[:, np.newaxis] + 6
+ np.random.normal(0, 1.3, (20, n))
)
y_b = (
1.8 * np.sin(x + 1)[:, np.newaxis] + 5
+ np.random.normal(0, 0.9, (20, n))
)
# ===================== CI 计算函数 =====================
def calculate_95ci(y_samples):
mean = np.mean(y_samples, axis=1)
sd = np.std(y_samples, axis=1, ddof=1)
sem = sd / np.sqrt(y_samples.shape[1])
t_crit = stats.t.ppf(0.975, df=y_samples.shape[1] - 1)
return mean, mean - t_crit * sem, mean + t_crit * sem
ctrl_m, ctrl_l, ctrl_u = calculate_95ci(y_ctrl)
a_m, a_l, a_u = calculate_95ci(y_a)
b_m, b_l, b_u = calculate_95ci(y_b)
colors = ['#1f77b4', '#ff7f0e', '#2ca02c']
labels = ['Control', 'Treat A', 'Treat B']
# ===================== 绘图 =====================
fig, ax = plt.subplots(figsize=(3.94, 2.76))
for m, l, u, c, lab in zip(
[ctrl_m, a_m, b_m],
[ctrl_l, a_l, b_l],
[ctrl_u, a_u, b_u],
colors, labels):
ax.fill_between(x, l, u, color=c, alpha=0.3)
ax.plot(x, m, color=c, linewidth=2.0, label=lab)
ax.set_title('Multi-Group 95% CI Curve Comparison')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.legend(frameon=False, ncol=3)
ax.grid(axis='y', alpha=0.2)
plt.show()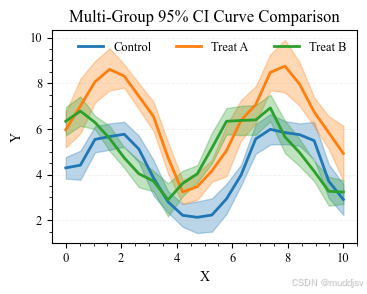
多组对比要点
- 每组独立计算 CI
- 配色高区分度、透明度统一
- 图例横排,避免遮挡数据
四、高级融合:CI 曲线 + 拟合模型 + 实验数据
在高水平论文中,常将原始数据、CI 曲线与拟合模型整合于同一图表,用于同时说明实验结果、统计不确定性与潜在函数关系。
推荐绘制顺序为: CI 区间带 → 拟合曲线 → 均值趋势 → 数据点
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
from scipy.optimize import curve_fit
set_scientific_plot_style()
np.random.seed(42)
x = np.linspace(0.5, 6, 25)
n = 18
y_true = 3.0 * (1 - np.exp(-0.6 * x)) + 0.5
y_samples = y_true[:, None] + np.random.normal(0, 0.3, (25, n))
def calculate_95ci(y):
m = np.mean(y, axis=1)
sem = stats.sem(y, axis=1)
t = stats.t.ppf(0.975, y.shape[1]-1)
return m, m - t*sem, m + t*sem
y_mean, ci_l, ci_u = calculate_95ci(y_samples)
def exp_fun(x, a, b, c):
return a * (1 - np.exp(-b * x)) + c
params, _ = curve_fit(exp_fun, x, y_mean)
x_fit = np.linspace(x.min(), x.max(), 100)
y_fit = exp_fun(x_fit, *params)
fig, ax = plt.subplots(figsize=(3.54, 2.76))
ax.fill_between(x, ci_l, ci_u, alpha=0.3)
ax.plot(x_fit, y_fit, '--', linewidth=2)
ax.plot(x, y_mean, linewidth=1.8)
ax.scatter(x, y_mean, s=15, zorder=5)
ax.set_title('CI Curve with Nonlinear Fitting')
ax.set_xlabel('Concentration')
ax.set_ylabel('Response')
ax.grid(axis='y', alpha=0.2)
plt.show()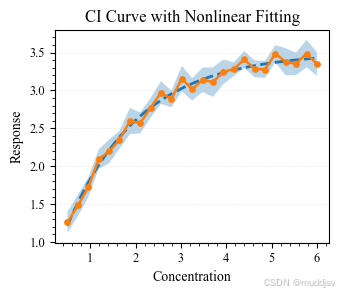
五、柱状图叠加 95% CI:组间比较的推荐形式
在组间比较研究中,"均值 + 95% CI"的柱状图比传统的 SD / SEM 更符合统计推断逻辑。
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
set_scientific_plot_style()
np.random.seed(42)
groups = ['Control', 'A', 'B', 'C']
n = 10
samples = [
np.random.normal(8.5, 1.2, n),
np.random.normal(12.3, 1.5, n),
np.random.normal(10.8, 1.1, n),
np.random.normal(14.2, 1.3, n)
]
means = []
errors = []
t = stats.t.ppf(0.975, n-1)
for s in samples:
m = np.mean(s)
sem = stats.sem(s)
means.append(m)
errors.append([t*sem, t*sem])
errors = np.array(errors).T
fig, ax = plt.subplots(figsize=(3.54, 2.36))
ax.bar(groups, means, yerr=errors, capsize=4)
ax.set_title('Bar Plot with 95% CI')
ax.set_ylabel('Mean Value')
ax.grid(axis='y', alpha=0.2)
plt.show()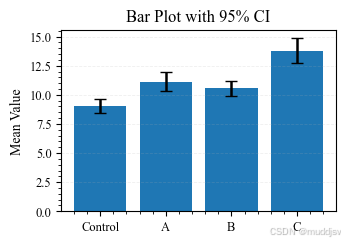
六、总结
CI 曲线是科研可视化中同时兼顾趋势表达与统计推断的核心图形形式。只要严格保证:
- CI 计算方法与样本量匹配
- 图层顺序合理
- 样式简洁克制
- 信息表达完整
CI 曲线就可以成为论文中最具说服力的结果展示方式之一。