八皇后问题 - 技术栈

题目描述

在一个8×8的棋盘上放置8个皇后，并使它们相互不能攻击，即同一列、同一个对角线、同一行不能多于一个以上的皇后。求出所有的放置方案，例如，下图为一种放置方案。

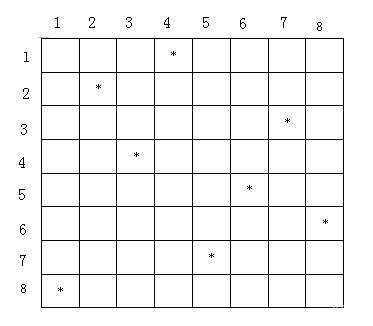
输入格式

无

输出格式

先输入若干行，每行八个数，第 i 个数表示第 i 行的皇后所在的列，方案按字典序输出。最后再一行输出一个数表示方案总数。

样例

【样例输出】

复制代码

3 1 6 2 5 7 4 1
.........
92

一些想法

因为这道题是求每一行棋子放的列是什么。

先开三个标记数组（标记每一列、正对角线和副对角线是否有摆棋子）和一个储存数组（输出用），并且一个记录方案数的变量。

我们可以递归每一行，从第 1 行遍历到第 8 行。如果当前行数大于 8 （遍历完 8 行了），输出每一行的列，将方案数加一，换行，返回。

否则，循环当前行的每一列，如果当前列没有被标记过（没有摆棋子）并且反对角线（右上到左下）没有被标记（没有摆棋子）并且正对角线（左上到右下）没有被标记（没有摆棋子），就确定了这个位置可以摆棋子，记录当前行的列，标记列、正对角线和副对角线为摆了棋子，递归下一行。回溯将列、正对角线和副对角线重置。

最后再输出方案总数。

列、正对角线和副对角线的表示方式（图为标准）：

列：直接用循环到当前的列。

正对角线（左上到右下）：当前行减当前列加 8（行减列最小是 1-8=-7 ，下标不能是负数，所以加一个使任何结果都为正数定值，避免负数）。往右走行加一，往下走列加一，行加一减列加一等于行减列，那么同一主对角线，行减列会是一个定值，为了避免负数，加上 8，那么在同一主对角线，行减列加 8 会是一个正数定值。

反对角线（右上到左下）：当前行加当前列。因为从右上到左下，向左走列减一，向下走行加一，所以同一副对角线，行加列就等于列减一加行加一，-1 和 1 互相抵消，就剩下行加列了。

根据这样（两条对角线），每一条对角线都有定值。

AC代码

cpp 复制代码

#include<bits/stdc++.h>
using namespace std;
int sum;
int a[15],b[15],c[15],d[15];
void zs(int hang){
	if(hang>8){
		sum++;
		for(int i=1;i<=8;i++){
			cout<<a[i]<<" ";
		}
		cout<<endl;
		return ;
	}
	for(int i=1;i<=8;i++){
		if(b[i]==0&&c[hang+i]==0&&d[hang-i+8]==0){
			a[hang]=i;
			b[i]=1;
			c[hang+i]=1;
			d[hang-i+8]=1;
			zs(hang+1);
			b[i]=0;
			c[hang+i]=0;
			d[hang-i+8]=0;
		}
	}
}
int main(){
	zs(1);
	cout<<sum;
	return 0;
}