【光学仿真】02：PSI Algorithm：基于Fringe索引的Zernike拟合全流程——从干涉图仿真到波前重构

文章目录

[PSI Algorithm：基于Fringe索引的Zernike拟合全流程------从干涉图仿真到波前重构](#PSI Algorithm：基于Fringe索引的Zernike拟合全流程——从干涉图仿真到波前重构)
- [📖 项目介绍](#📖 项目介绍)
- [✨ 核心特性](#✨ 核心特性)
- [🛠️ 环境配置](#🛠️ 环境配置)
- - 依赖库
  - 安装方式
- [🚀 快速开始](#🚀 快速开始)
- - 运行完整流程
  - 核心功能示例
  - - [1. 生成统一网格](#1. 生成统一网格)
    - [2. 生成Fringe Zernike多项式](#2. 生成Fringe Zernike多项式)
    - [3. 仿真相移干涉图](#3. 仿真相移干涉图)
    - [4. Zernike多项式拟合](#4. Zernike多项式拟合)
- [📂 代码结构](#📂 代码结构)
- [📊 结果展示](#📊 结果展示)
- - [1. 单位圆掩码](#1. 单位圆掩码)
  - [2. 4步相移干涉图](#2. 4步相移干涉图)
  - [3. 包裹/解包裹相位](#3. 包裹/解包裹相位)
  - [4. Zernike拟合结果](#4. Zernike拟合结果)
- [🎯 核心原理](#🎯 核心原理)
- - [1. Fringe Zernike索引规则](#1. Fringe Zernike索引规则)
  - [2. Zernike多项式定义](#2. Zernike多项式定义)
  - [3. 相移干涉术原理](#3. 相移干涉术原理)
  - [4. 最小二乘拟合](#4. 最小二乘拟合)
- [📄 许可证](#📄 许可证)

PSI Algorithm：基于Fringe索引的Zernike拟合全流程------从干涉图仿真到波前重构

基于 Fringe索引规则 的Zernike多项式实现光学干涉测量全流程：干涉图仿真 → 相位提取 → 相位解包裹 → Zernike多项式拟合，适用于光学干涉算法验证、Zernike多项式学习与研究。

📖 项目介绍

本项目围绕Fringe索引（区别于传统ANSI Zernike索引）的Zernike多项式展开，实现了从干涉图仿真到Zernike拟合的端到端流程：

统一网格/极坐标/圆形掩码生成，避免多模块极径处理不一致问题；
自动生成Fringe索引的Zernike多项式（含正交归一化），支持表达式打印、可视化；
仿真带噪声的多步相移干涉图（支持4步相移）；
基于相移算法提取包裹相位，通过区域增长法解包裹；
最小二乘拟合Zernike系数，量化对比真实/拟合相位与系数；
全流程可视化，直观展示每一步结果。

✨ 核心特性

鲁棒的网格处理 ：封装GridGenerator类，统一管理笛卡尔/极坐标网格、单位圆掩码，避免手动修改极径导致的逻辑错误；
标准Zernike实现：严格遵循Fringe索引规则，支持Zernike多项式表达式自动生成、正交归一化；
高保真仿真：支持添加高斯噪声、调制深度配置，模拟真实干涉图特性；
完整流程验证：从干涉图仿真到拟合结果量化，全流程自验证，便于算法调试；
友好的可视化：提供干涉图、包裹/解包裹相位、真实/拟合相位、系数对比等多维度可视化。

🛠️ 环境配置

依赖库

Plain 复制代码

matplotlib==3.10.8
numpy==2.4.2
scipy==1.17.0
skimage==0.0

安装方式

Bash 复制代码

# 克隆仓库
git clone https://github.com/seatonyang/PSI-Algorithm.git
cd PSI-Algorithm

# 安装依赖
pip install -r requirements.txt
# 或手动安装
pip install numpy scipy matplotlib

🚀 快速开始

运行完整流程

Bash 复制代码

# 运行主程序（含仿真→提取→解包裹→拟合→可视化）
python main.py

核心功能示例

1. 生成统一网格

python 复制代码

from grid_utils import GridGenerator

# 生成512×512网格（-1~1笛卡尔坐标，0~√2极径）
grid = GridGenerator(size=512)
print(f"网格尺寸：{grid.size}×{grid.size}")
print(f"单位圆有效像素数：{np.sum(grid.circle_mask)}")

2. 生成Fringe Zernike多项式

python 复制代码

from fringe_zernike_generator import FringeZernike

# 初始化Zernike生成器（8阶，基于统一网格）
zernike_gen = FringeZernike(max_order=8, grid=grid)

# 生成第4阶（Focus）多项式
z4 = zernike_gen.generate(4)
# 打印多项式表达式
zernike_gen.print_zernike_expression(index=4)
# 可视化单个多项式
zernike_gen.plot_single(index=4, cmap="jet")

3. 仿真相移干涉图

python 复制代码

from interferogram_simulation import InterferogramSimulator
import numpy as np

# 配置真实Zernike系数（8阶）
true_coeffs = np.zeros(8)
true_coeffs[1] = 0.6  # Tilt x
true_coeffs[3] = 1.2  # Focus
true_coeffs[4] = 0.9  # Astigmatism x

# 4步相移量
phase_shifts = [0, np.pi/2, np.pi, 3*np.pi/2]

# 初始化仿真器
simulator = InterferogramSimulator(
    grid=grid,
    max_order=8,
    true_coeffs=true_coeffs,
    phase_shifts=phase_shifts,
    noise_std=0.03  # 高斯噪声标准差
)

# 生成干涉图和真实相位
interferograms, true_phase = simulator.generate()
print(f"干涉图形状：{interferograms.shape}")  # (4, 512, 512)

4. Zernike多项式拟合

python 复制代码

from zernike_fitting import ZernikeFitter

# 初始化拟合器（基于解包裹相位）
fitter = ZernikeFitter(
    grid=grid,
    unwrapped_phase=unwrapped_phase,  # 解包裹后的相位
    max_order=8
)

# 最小二乘拟合
fitted_coeffs, fitted_phase = fitter.fit()

# 打印拟合结果
coeff_rmse = np.sqrt(np.mean((true_coeffs - fitted_coeffs)**2))
phase_rmse = np.sqrt(np.nanmean((true_phase - fitted_phase)**2))
print(f"系数拟合RMSE：{coeff_rmse:.6f}")
print(f"相位拟合RMSE：{phase_rmse:.6f}")

📂 代码结构

文件	核心功能
`grid_utils.py`	统一网格生成工具：笛卡尔/极坐标网格、单位圆掩码、相位标准化
`fringe_zernike_generator.py`	Fringe Zernike多项式生成：索引映射、径向/角向多项式、可视化、表达式打印
`interferogram_simulation.py`	相移干涉图仿真：基于Zernike相位生成带噪声的干涉图
`phase_extraction.py`	相位提取：从相移干涉图中提取包裹相位
`phase_unwrapping.py`	相位解包裹：区域增长法解包裹，恢复连续相位
`zernike_fitting.py`	Zernike拟合：最小二乘拟合Zernike系数，生成拟合相位
`main.py`	主程序：串联全流程（仿真→提取→解包裹→拟合→可视化）
`requirements.txt`	依赖库清单

📊 结果展示

1. 单位圆掩码

2. 4步相移干涉图

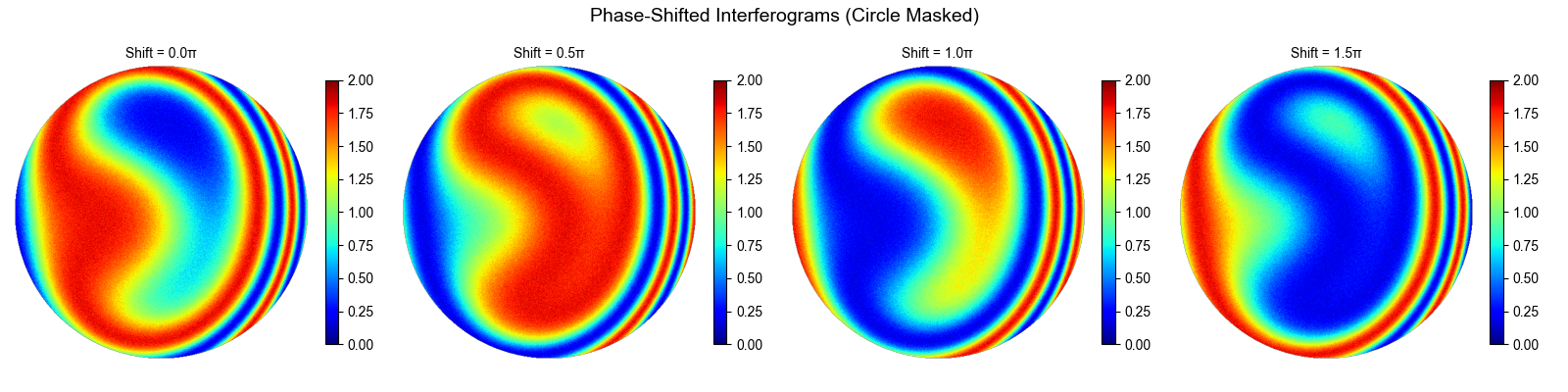
3. 包裹/解包裹相位

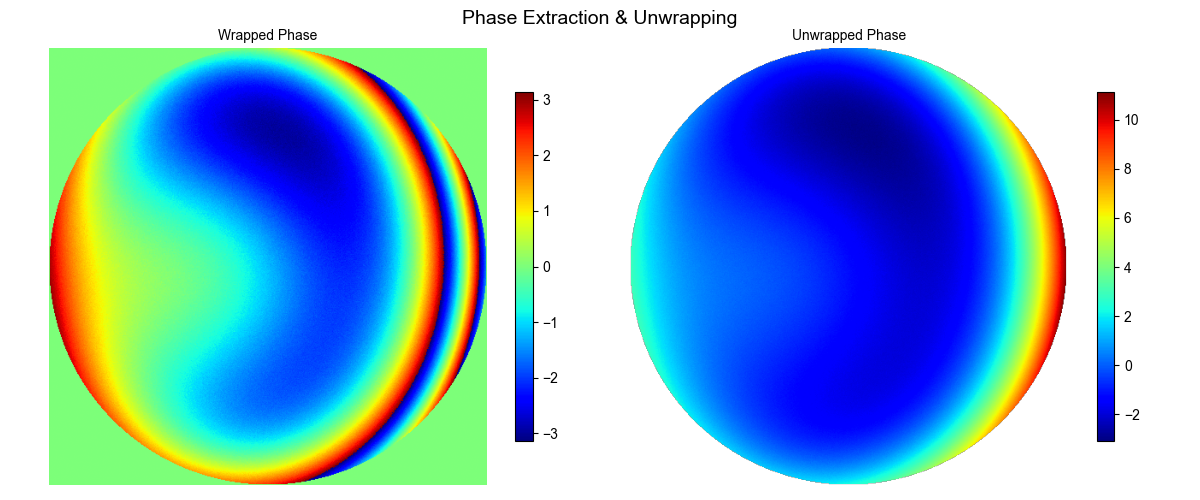
4. Zernike拟合结果

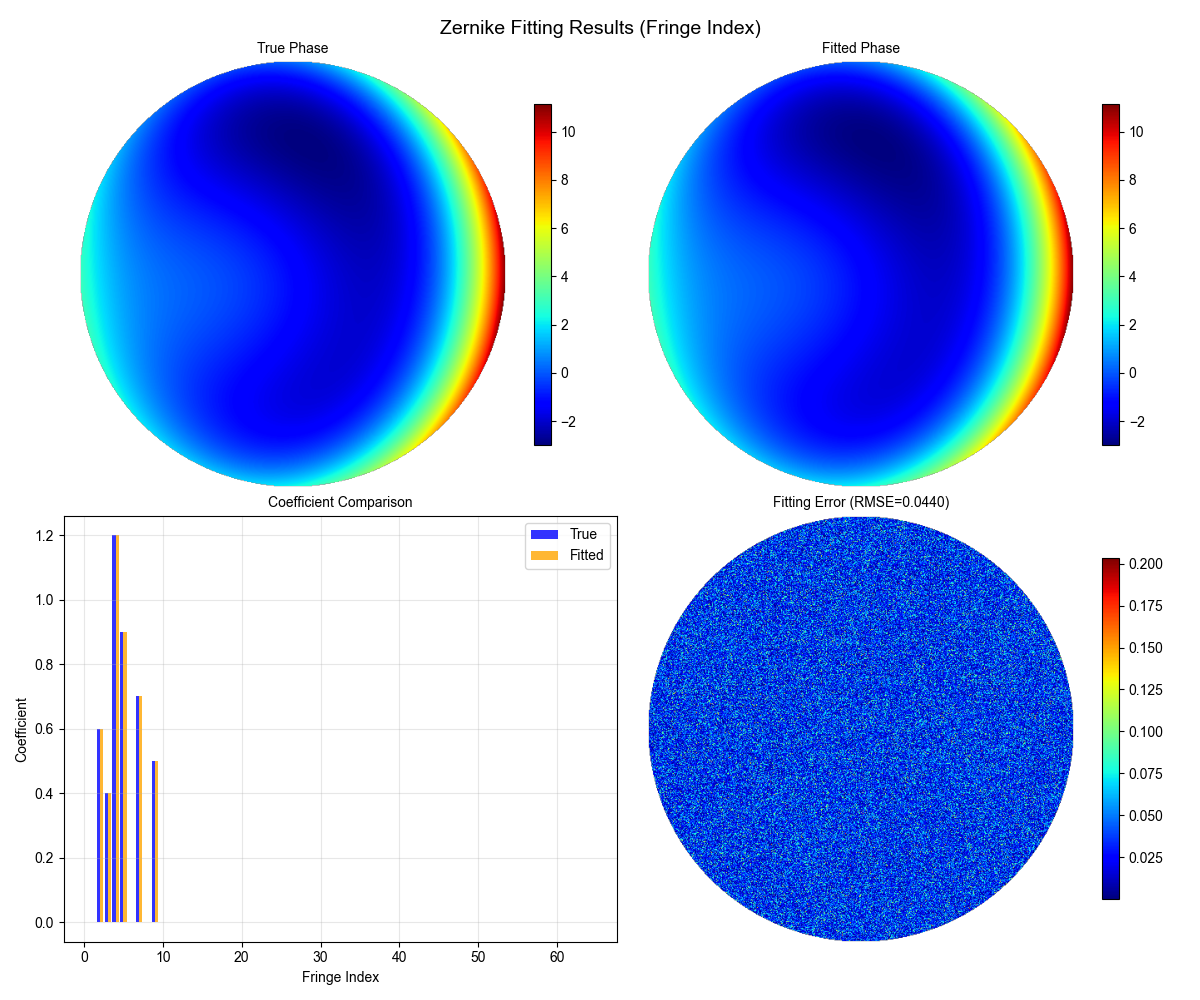
🎯 核心原理

1. Fringe Zernike索引规则

Fringe索引按s = m + k分组（m为角向阶数，k为径向子阶数），每组内按m递减排列，m=0时为纯径向项，m≠0时分为cos(mθ)（x向）和sin(mθ)（y向）项。

2. Zernike多项式定义

Z n m ( r , θ ) = R n m ( r ) × { 1 ( m = 0 ) cos ⁡ ( m θ ) ( m > 0 , cos项 ) sin ⁡ ( m θ ) ( m > 0 , sin项 ) Z_n^m(r,θ) = R_n^m(r) × \begin{cases} 1 & (m=0) \\ \cos(mθ) & (m>0, \text{cos项}) \\ \sin(mθ) & (m>0, \text{sin项}) \end{cases} Znm(r,θ)=Rnm(r)×⎩ ⎨ ⎧1cos(mθ)sin(mθ)(m=0)(m>0,cos项)(m>0,sin项)

其中径向多项式 R n m ( r ) R_n^m(r) Rnm(r) 满足：

R n m ( r ) = ∑ s = 0 ( n − m ) / 2 ( − 1 ) s ( n − s ) ! s ! ( n + m 2 − s ) ! ( n − m 2 − s ) ! r n − 2 s R_n^m(r) = \sum_{s=0}^{(n-m)/2} \frac{(-1)^s (n-s)!}{s! \left(\frac{n+m}{2}-s\right)! \left(\frac{n-m}{2}-s\right)!} r^{n-2s} Rnm(r)=∑s=0(n−m)/2s!(2n+m−s)!(2n−m−s)!(−1)s(n−s)!rn−2s

3. 相移干涉术原理

4步相移干涉图的光强分布：

I i = I 0 [ 1 + γ cos ⁡ ( ϕ + δ i ) ] I_i = I_0 \left[1 + \gamma \cos(\phi + \delta_i)\right] Ii=I0[1+γcos(ϕ+δi)]

其中 ϕ \phi ϕ 为待测相位， δ i \delta_i δi 为相移量，通过4步相移算法提取相位：

ϕ = arctan ⁡ ( I 4 − I 2 I 1 − I 3 ) \phi = \arctan\left(\frac{I_4 - I_2}{I_1 - I_3}\right) ϕ=arctan(I1−I3I4−I2)

4. 最小二乘拟合

将解包裹相位分解为Zernike基的线性组合：

ϕ ( r , θ ) = ∑ i = 1 N c i Z i ( r , θ ) \phi(r,θ) = \sum_{i=1}^N c_i Z_i(r,θ) ϕ(r,θ)=∑i=1NciZi(r,θ)

通过最小二乘求解系数 c i c_i ci ：

c ^ = arg ⁡ min ⁡ c ∥ ϕ − A Z ∥ 2 2 \hat{c} = \arg\min_c \| \phi - AZ \|_2^2 c^=argminc∥ϕ−AZ∥22

其中 A A A 为Zernike基底矩阵， Z Z Z 为Zernike多项式向量。

📄 许可证

本项目采用MIT许可证 - 详见<LICENSE>文件。