98. 验证二叉搜索树
java
class Solution {
static List<Integer> list;
public boolean isValidBST(TreeNode root) {
list = new ArrayList<>();
helper(root);
int size = list.size();
for (int i = 1; i < size; i++) {
if (list.get(i-1) >= list.get(i)) return false;
}
return true;
}
// 中序遍历
static void helper(TreeNode node) {
if (node == null) return;
helper(node.left);
list.add(node.val);
helper(node.right);
}
}解题思路:按照题目的要求可以知道如果按照左根右的中序遍历出来的结果一定是递增的
96. 不同的二叉搜索树
java
class Solution {
public int numTrees(int n) {
// dp[i] 1到i这个范围能构建的二叉树数量
int[] dp = new int[n + 1];
dp[0] = 1; // 因为涉及到乘法,所以要初始化为1
// 枚举1~i这个范围
for (int i = 1; i <= n; i++) {
// 在1~i这个范围找节点j作为根节点,算出它的构造方式
for (int j =1; j <= i; j++) {
dp[i] += dp[j-1] * dp[i-j];
}
}
return dp[n];
}
}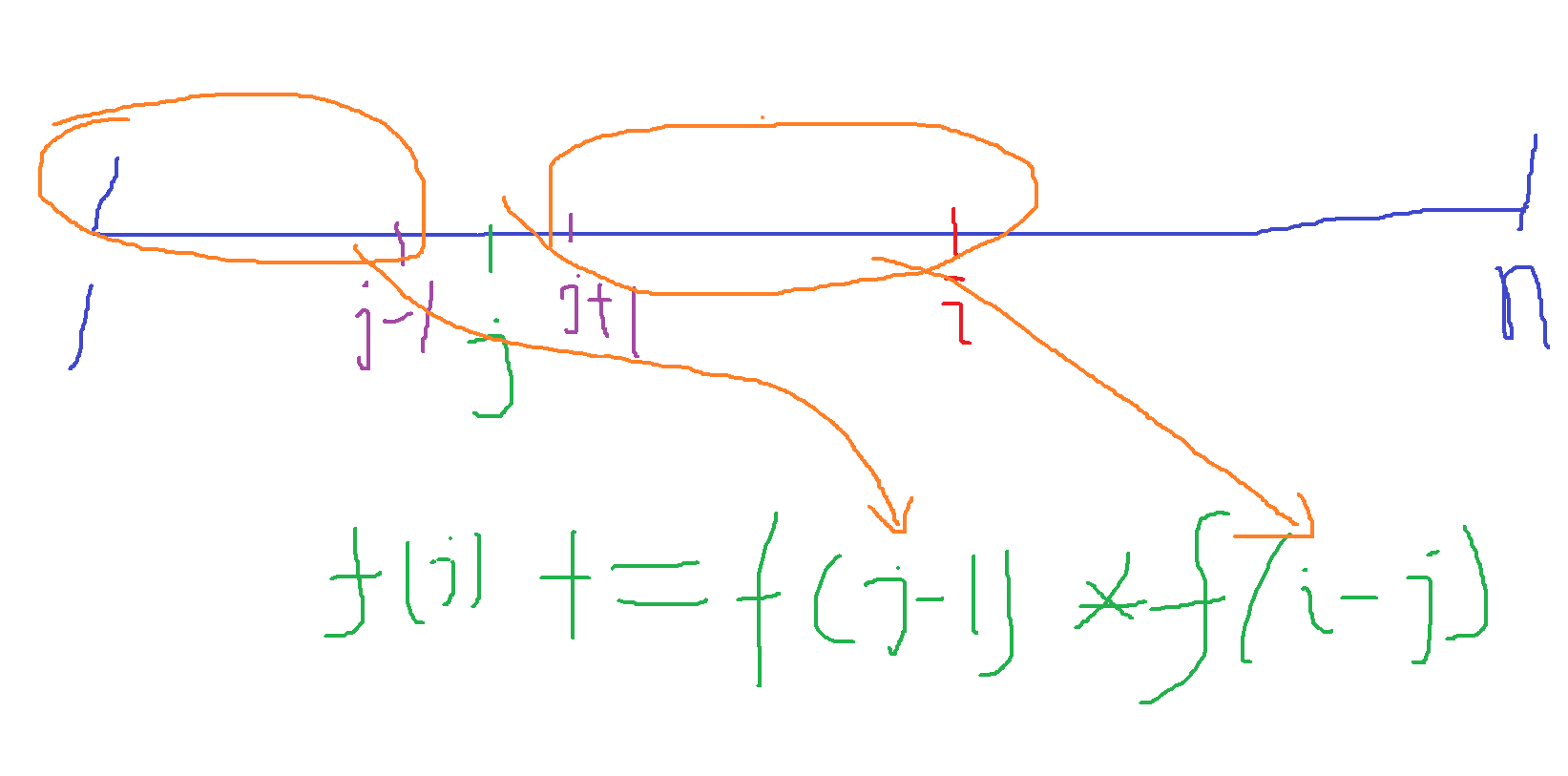
解题思路:先按照上面的图求出递推公式
这里累加的原因是因为j可以在1~i中不断地进行枚举,所以需要各个位置都统计起来
94. 二叉树的中序遍历
java
class Solution {
static List<Integer> res;
public List<Integer> inorderTraversal(TreeNode root) {
res = new ArrayList<>();
dfs(root);
return res;
}
static void dfs(TreeNode node) {
if (node == null) return;
dfs(node.left);
res.add(node.val);
dfs(node.right);
}
}84. 柱状图中最大的矩形
java
class Solution {
public int largestRectangleArea(int[] heights) {
int n = heights.length;
int[] left = new int[n]; // 存储以当前元素为高度地左边界
Arrays.fill(left, -1);
int[] right = new int[n]; // 存储以当前元素为高度地右边界
Arrays.fill(right, n);
Deque<Integer> deque = new LinkedList<>();
for (int i = 0; i < n; i++) {
while (!deque.isEmpty() && heights[i] < heights[deque.peek()]) {
// 栈顶元素的右边界确定了
int idx = deque.poll();
right[idx] = i;
}
// 经过上面的循环之后,栈还不为空说明当前元素比栈顶元素大,所以当前元素的左边界确定了
if (!deque.isEmpty()) {
left[i] = deque.peek();
}
deque.push(i);
}
// 计算结果
int ans = 0;
for (int i = 0; i < n; i++) {
int w = right[i] - left[i] - 1;
int area = w * heights[i];
ans = Math.max(area, ans);
}
return ans;
}
}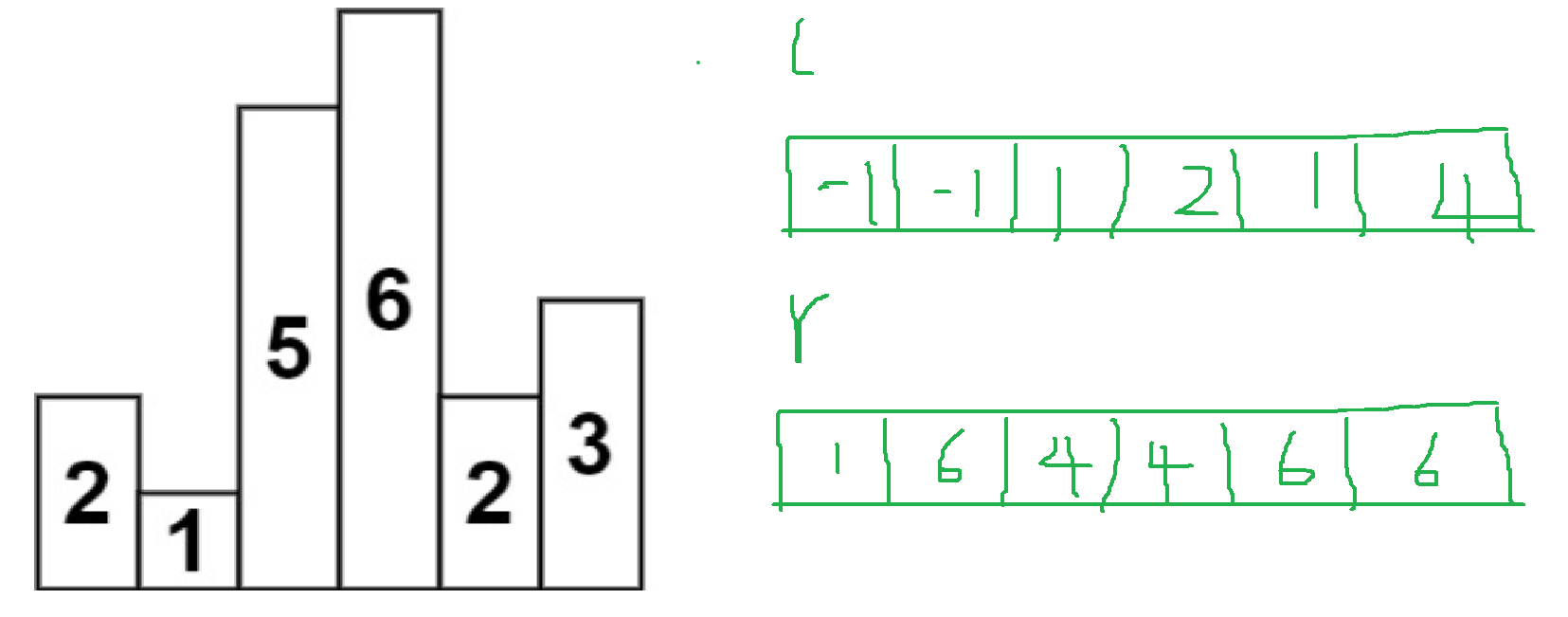
初始化:
- l数组记录左边第一个比它小的元素的下标
- r数组记录右边第一个比它小的元素的下标
- 初始化的时候分别为-1和n,这个很容易就能推断出为什么要这样做
然后就是进行推断的过程,这里是通过单调栈来实现,但是我们先不去管为什么选这个数据结构,先从本质触发,无非就是枚举每一个元素作为高度,求它能达到的最大面积,最后统计整个过程的最大面积
但是如果直接循环的话,时间复杂度就是 O(n^2) ,但是我们可以用单调栈来求每一个元素的左右第一个小于它的下标
- 每次只要判断到栈顶元素大于当前元素,那就说明栈顶元素的右边第一个小于它的元素就是当前元素
- 循环之后,如果栈不为空,那就说明此时栈顶的元素是小于当前元素的,那是不是就说明当前元素的左边第一个小于它的元素就是栈顶元素
85. 最大矩形
https://leetcode.cn/problems/maximal-rectangle/description/?envType=problem-list-v2&envId=2cktkvj
java
class Solution {
public int maximalRectangle(char[][] matrix) {
int res = 0;
int m = matrix.length;
int n = matrix[0].length;
int[] heights = new int[n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == '0') {
heights[j] = 0;
} else {
heights[j] ++;
}
}
res = Math.max(res, helper(heights));
}
return res;
}
static int helper(int[] heights) {
Deque<Integer> deque = new LinkedList<>();
int n = heights.length;
// 存储当前元素左边第一个小于它的下标
int[] left = new int[n];
Arrays.fill(left, -1);
// 存储当前元素右边第一个小于它的下标
int[] right = new int[n];
Arrays.fill(right, n);
for (int i = 0; i < n; i++) {
// 找到栈顶元素的右边第一个小于它的元素下标
while (!deque.isEmpty() && heights[i] < heights[deque.peek()]) {
int idx = deque.poll();
right[idx] = i;
}
// 找到当前元素左边第一个小于它的元素下标(即当前栈顶元素)
if (!deque.isEmpty()) {
left[i] = deque.peek();
}
deque.push(i);
}
// 统计面积
int res = 0;
for (int i = 0; i < n; i++) {
int w = right[i] - left[i] - 1;
int area = w * heights[i];
res = Math.max(res, area);
}
return res;
}
}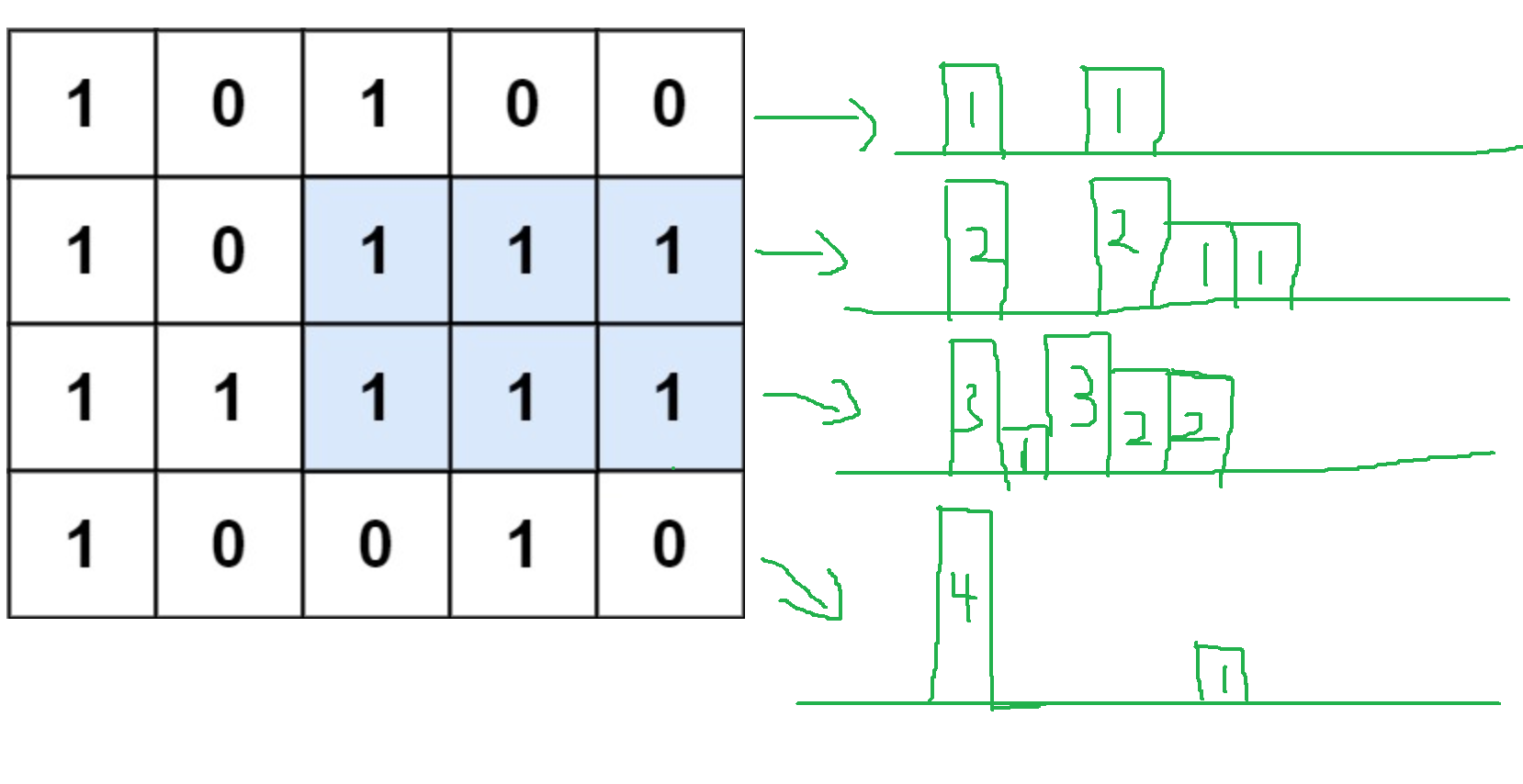
解题思路:和84一样,具体解的过程这里就不再赘诉,直接看84就行,这里主要讲一下如何转变成84来进行求解
具体的就是像上图一样,其实就是当成柱形图来进行计算,需要我们自己构建柱形图,其他的就没什么区别了