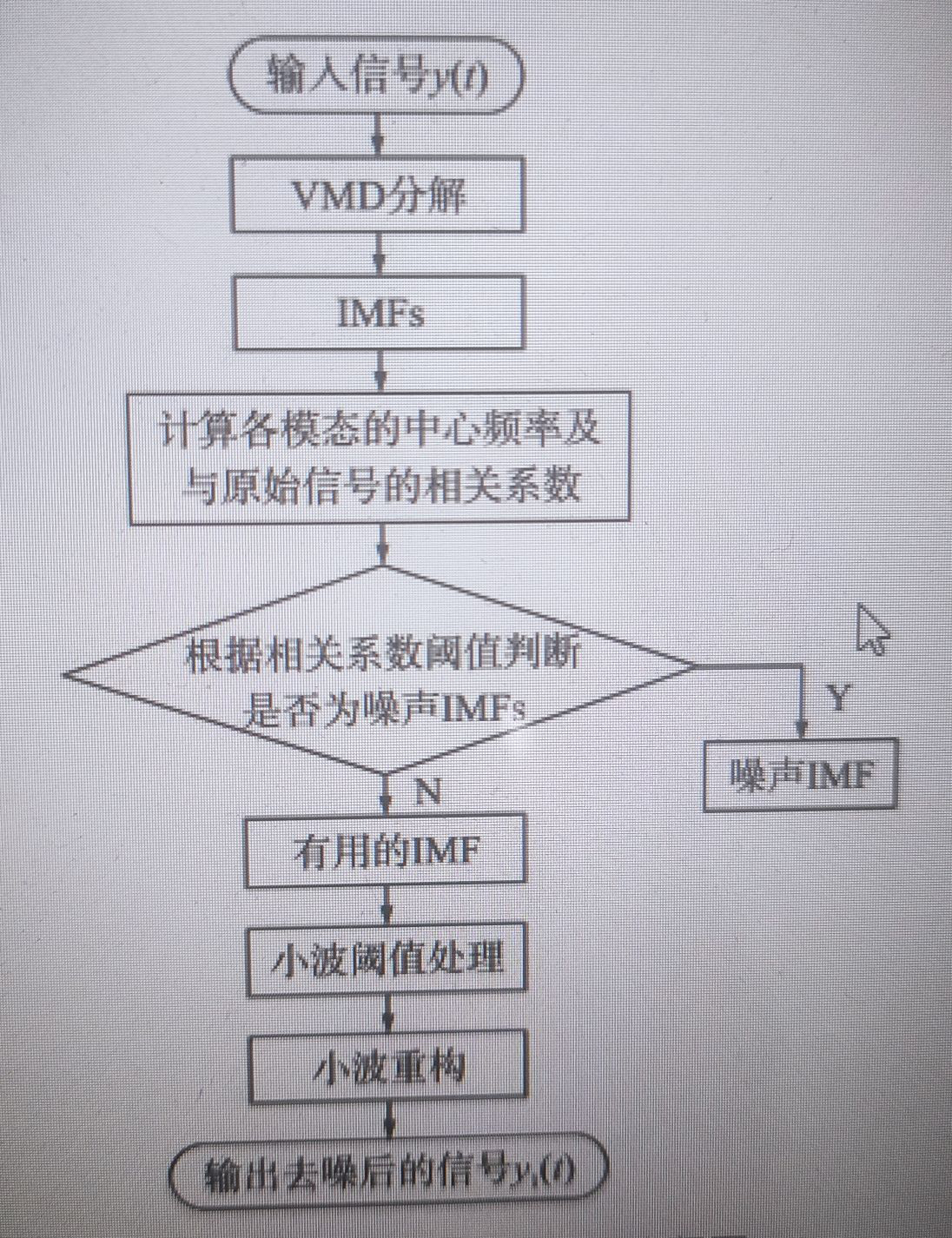
从excel中读取信号，首先计算信号的vmd分解，得到imf分量，然后根据imf分量与原始信号...

从excel中读取信号，首先计算信号的vmd分解，得到imf分量，然后根据imf分量与原始信号的相关系数确定出信号imf喝噪声imf，对有用的imf进行小波阈值滤波，最后对滤波后的imf进行重构输出信号下图是流程图盒vmd分解结果的时域后频谱

一、概述

本文档将详细解读两组信号处理相关的MATLAB代码集合，分别是基于VMD（变分模态分解）与小波阈值的信号降噪代码，以及基于EEMD/CEEMD（集合经验模态分解/互补集合经验模态分解）与样本熵的信号分解与频段划分代码。两组代码均围绕信号的分解、特征提取、降噪或频段分离展开，适用于不同场景下的信号处理需求，如含噪信号的降噪处理、复杂信号的频段拆分与特征分析等。

二、基于VMD与小波阈值的信号降噪代码（VMD_corr_wavelet与仿真信号版本）

（一）核心功能

该代码集合的核心目标是对输入信号（真实信号或仿真信号）进行降噪处理。通过VMD分解将信号分解为多个固有模态函数（IMF），利用相关系数筛选出含有效信息的IMF分量，再通过小波阈值滤波对有效IMF分量进一步降噪，最终重构得到去噪信号。

（二）文件组成与分工

文件路径	文件名	核心功能
VMDcorrwavelet	Main1.m	真实信号处理主程序：读取Excel信号、VMD分解、相关系数计算、小波阈值滤波、信号重构与可视化
VMDcorrwavelet	VMD.m	变分模态分解核心函数：实现信号的VMD分解，输出IMF分量、分量频谱及中心频率
VMDcorrwavelet	plotIMF.m	IMF分量可视化函数：绘制IMF分量的时域波形与频域频谱
仿真信号VMD 阈值小波阈值处理合成降噪信号	Main1.m	仿真信号处理主程序：生成含噪仿真信号、VMD分解、相关系数计算、小波阈值滤波、信号重构与可视化
仿真信号VMD 阈值小波阈值处理合成降噪信号	VMD.m	同VMDcorrwavelet目录下的VMD.m，为VMD分解核心函数
仿真信号VMD 阈值小波阈值处理合成降噪信号	plotIMF.m	增强版IMF可视化函数：支持输入采样频率，优化频谱绘制的频率轴精度

（三）核心算法流程

1. 信号输入与预处理

真实信号版本（VMDcorrwavelet/Main1.m） ：通过xlsread('25.xlsx')读取Excel文件中的时间序列数据，分离时间列（time）与信号列（signal）。
仿真信号版本（仿真信号目录/Main1.m） ：生成频率为300Hz的正弦信号y=0.01sin(2 pi300t)，通过awgn函数添加噪声（信噪比-8.986dB），得到含噪信号y_noise，并绘制原始信号、含噪信号及其频谱。

2. VMD分解参数配置与执行

VMD分解的核心参数及含义如下：

参数	含义	真实信号配置	仿真信号配置
alpha	带宽约束平衡参数	2000	6000
tau	对偶上升时间步长（噪声容限）	1	0
K	分解模态数量	8	8
DC	是否强制第一模态为直流分量	1（是）	1（是）
init	中心频率初始化方式	1（均匀分布）	1（均匀分布）
tol	收敛判据容差	1e-6	1e-7

通过调用[u, u_hat, omega] = VMD(signal, alpha, tau, K, DC, init, tol)执行分解，输出：

u：K个IMF分量（K×N矩阵，N为信号长度）；
u_hat：各IMF分量的频谱；
omega：各IMF分量的估计中心频率。

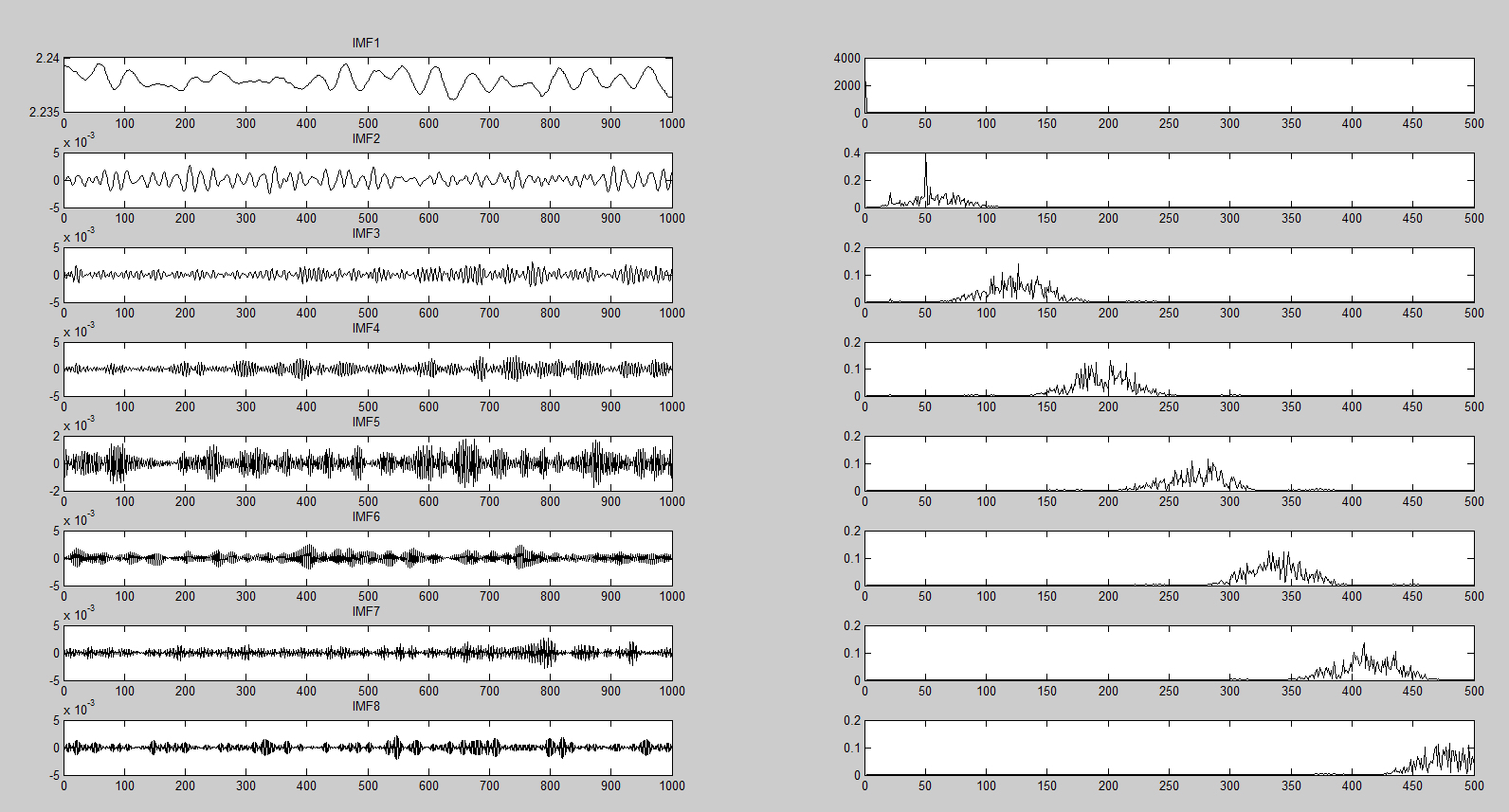
3. IMF分量可视化

调用plotIMF函数绘制每个IMF分量的时域波形（左子图）与频域频谱（右子图），仿真信号版本的plotIMF支持输入采样频率fs，使频谱的频率轴更精准。

4. 相关系数计算与有效IMF筛选

通过循环计算每个IMF分量与原始信号（真实信号为输入信号，仿真信号为无噪原始信号）的相关系数：

matlab 复制代码

for i=1:size(u,1)
    [r(i),p(i)] = corr(signal,u(i,:)'); % 计算相关系数r与显著性p
    disp(['IMF',num2str(i),'相关系数为：',num2str(r(i))]);
end

设置相关系数阈值TH（真实信号TH=0.38，仿真信号TH=0.02），筛选出相关系数≥TH的IMF分量（视为含有效信息），其余分量视为噪声。

5. 小波阈值滤波

对筛选出的有效IMF分量，调用MATLAB内置函数wden进行小波阈值降噪：

真实信号版本：imfdwavelet_temp=wden(u(i,:),'rigrsure','s','mln',3,'sym7')
仿真信号版本：imfdwavelet_temp=wden(u(i,:),'rigrsure','s','one',5,'sym7')

wden函数参数说明：

参数	含义	配置值
信号	输入IMF分量	u(i,:)
阈值选择规则	'rigrsure'（自适应阈值）	固定
阈值应用方式	's'（软阈值）	固定
分解层数	真实信号3层，仿真信号5层	3/5
小波基函数	'sym7'（7阶Symlet小波）	固定

6. 信号重构与结果可视化

将降噪后的有效IMF分量求和，得到重构去噪信号：signalr = sum(imfd_wavelet,1)。

通过2×2子图展示结果：

原始信号（含噪）时域波形；
原始信号频域频谱；
去噪信号时域波形；
去噪信号频域频谱。

（四）关键差异说明

对比维度	真实信号版本	仿真信号版本
信号来源	Excel文件读取	程序生成正弦含噪信号
相关系数对比对象	输入的原始信号	无噪的仿真原始信号
VMD参数	alpha=2000，tau=1，tol=1e-6	alpha=6000，tau=0，tol=1e-7
小波滤波参数	分解层数3，阈值尺度'mln'	分解层数5，阈值尺度'one'
可视化功能	基础时域+频谱绘制	支持采样频率输入，频谱频率轴更精准

三、基于EEMD/CEEMD与样本熵的信号分解与频段划分代码（eemd+sampleEntropy_0329214035）

（一）核心功能

该代码集合的核心目标是对复杂信号进行自适应分解与频段划分。通过EEMD或CEEMD将信号分解为多个IMF分量，计算各IMF分量的样本熵（反映信号复杂度），根据样本熵阈值将IMF分量划分为低频、中频、高频三组，实现信号的频段分离与特征提取。

（二）文件组成与分工

文件路径	文件名	核心功能
ceemd+样本熵	Main.m	CEEMD分解主程序：读取信号、CEEMD分解、IMF可视化、样本熵计算、频段划分与重构
ceemd+样本熵	ceemd.m	互补集合经验模态分解函数：通过添加正负成对噪声降低模态混叠，输出IMF分量
ceemd+样本熵	extrema.m	极值点检测函数：用于EMD类分解中的上下包络线拟合
ceemd+样本熵	sampleEntropy.m	样本熵计算函数：基于Chebyshev距离计算信号的样本熵
eemd+样本熵\v1	Main.m	EEMD分解主程序：读取信号、EEMD分解、IMF可视化、样本熵计算、频段划分与重构
eemd+样本熵\v1	eemd.m	集合经验模态分解函数：通过添加高斯白噪声降低模态混叠，输出IMF分量
eemd+样本熵\v1	extrema.m	同ceemd+样本熵目录下的extrema.m，为极值点检测函数
eemd+样本熵\v1	sampleEntropy.m	同ceemd+样本熵目录下的sampleEntropy.m，为样本熵计算函数

（三）核心算法流程

1. 信号输入与参数配置

通过data=importdata('data.mat')读取MATLAB数据文件中的时间序列信号，配置核心参数：

采样频率Fs=600Hz（可默认设为1）；
时间向量t=linspace(0,1,L)（L为信号长度）；
频率轴f=Fs*(0:(L/2))/L（用于频谱绘制）。

2. EEMD/CEEMD分解

（1）CEEMD分解（ceemd+样本熵/Main.m）

调用imf = ceemd(data,0.2,100,5)'执行分解，参数说明：

参数	含义	配置值
Y	输入信号	data
Nstd	添加噪声的标准差与信号标准差比值	0.2
NE	集合平均次数	100
TNM	模态数量（不含趋势项）	5

CEEMD通过添加正负成对的高斯白噪声，对每次添加噪声后的信号进行EMD分解，最后对所有分解结果取平均，有效降低模态混叠。

（2）EEMD分解（eemd+样本熵\v1/Main.m）

调用eemd_imf = eemd(data,0.1,10)'执行分解，参数说明：

参数	含义	配置值
Y	输入信号	data
Nstd	添加噪声的标准差与信号标准差比值	0.1
NE	集合平均次数	10

EEMD通过添加单一高斯白噪声并多次分解取平均实现降噪，模态混叠抑制效果弱于CEEMD，但计算效率更高。

3. IMF分量可视化

通过循环绘制IMF分量的时域波形与频域频谱：

时域波形：按6个分量为一组绘制子图，标注IMF序号或"残差"；
频域频谱：对每个IMF分量进行FFT变换，绘制0~Fs/2范围内的频谱，标注对应IMF序号。

4. 样本熵计算

对每个IMF分量计算样本熵，反映分量的复杂度（样本熵越大，信号越复杂，通常对应高频噪声或复杂振动）：

matlab 复制代码

sampEn(i,1) = sampleEntropy(imf(i,:),2,0.2*std(imf(i,:)),1);

sampleEntropy函数参数说明：

参数	含义	配置值
seq	输入信号序列	imf(i,:)
wlen	窗口长度（维度）	2
r	相似度容差（通常为信号标准差的0.1~0.2倍）	0.2*std(imf(i,:))
shift	采样间隔（1为无下采样）	1

5. 基于样本熵的频段划分与重构

设置两个样本熵阈值Th1和Th2，将IMF分量划分为三组：

频段	样本熵条件	重构方式
低频	sampEn ≤ Th2	所有满足条件的IMF分量求和
中频	Th2 < sampEn < Th1	所有满足条件的IMF分量求和
高频	sampEn ≥ Th1	所有满足条件的IMF分量求和

阈值配置：

CEEMD版本：Th1=0.4，Th2=0.1；
EEMD版本：Th1=0.5，Th2=0.1。

最后绘制三组重构信号的时域波形与频域频谱，实现信号的频段分离。

（四）关键差异说明

对比维度	CEEMD版本（ceemd+样本熵）	EEMD版本（eemd+样本熵\v1）
分解算法	CEEMD（互补集合EMD）	EEMD（集合EMD）
抗模态混叠能力	强（添加正负成对噪声）	较弱（添加单一噪声）
分解参数	Nstd=0.2，NE=100，TNM=5	Nstd=0.1，NE=10（模态数量自动计算）
样本熵阈值	Th1=0.4，Th2=0.1	Th1=0.5，Th2=0.1
计算效率	较低（100次集合平均）	较高（10次集合平均）

四、适用场景与使用建议

（一）VMD+小波阈值降噪代码

适用场景

含噪信号的降噪处理，尤其适用于非线性、非平稳信号（如振动信号、声信号、生物医学信号）；
需保留信号主要特征，同时抑制随机噪声的场景；
已知信号大致频率范围，可通过调整VMD参数（如K、alpha）优化分解效果的场景。

使用建议

调整VMD参数：
- K（模态数量）：需根据信号复杂度调整，过多易导致过分解，过少易导致欠分解；
- alpha（带宽约束）：信号频率越高，alpha可适当增大（如仿真信号alpha=6000高于真实信号的2000）；
- TH（相关系数阈值）：根据实际信号的噪声强度调整，噪声越强，阈值可适当降低。
小波参数优化：
- 小波基函数：可替换为'db4'（db系列小波）、'haar'（ Haar小波）等，根据信号特征选择；
- 分解层数：信号长度越长，可适当增加分解层数（如仿真信号5层 vs 真实信号3层）。

（二）EEMD/CEEMD+样本熵频段划分代码

适用场景

复杂信号的频段分离（如将信号中的低频趋势、中频有效振动、高频噪声分离）；
信号特征提取（样本熵可作为信号复杂度指标，用于故障诊断、状态监测等）；
模态混叠问题较突出的信号（优先选择CEEMD）；
对计算效率有要求，模态混叠不严重的场景（可选择EEMD）。

使用建议

分解算法选择：
- 若信号模态混叠严重（如多频率成分叠加），优先使用CEEMD，通过增加NE（集合次数）提升效果；
- 若需快速处理，可选择EEMD，适当增大Nstd（噪声强度）平衡效果与效率。
样本熵与阈值调整：
- 样本熵窗口长度wlen：通常取2或3，可根据信号长度调整；
- 容差r：建议保留0.1~0.2倍标准差的配置，确保计算稳定性；
- 频段阈值Th1、Th2：可根据样本熵计算结果的分布调整，使三组频段的分量数量合理分配。

五、总结

两组代码集合分别针对信号处理的两大核心需求：降噪处理 与频段划分。VMD+小波阈值代码通过"分解-筛选-降噪-重构"的流程，高效实现含噪信号的净化；EEMD/CEEMD+样本熵代码通过"自适应分解-复杂度分析-频段划分"，实现复杂信号的结构化解析。

使用时需根据具体需求选择合适的算法：若目标是降噪，优先选择VMD+小波阈值方案；若目标是信号频段分离或特征提取，优先选择EEMD/CEEMD+样本熵方案（模态混叠严重时选CEEMD，效率优先时选EEMD）。同时，需根据信号特性（如频率范围、噪声强度、复杂度）灵活调整核心参数，以达到最优处理效果。