队列 | 二叉树

一、队列

遵循"先进先出，后进后出"的原则

1.队头：出队的一端；

队尾：入队的一端；

2.循环队列

队空：Head == Tail（队头和队尾指针指向同一位置）；
队满：(Tail + 1) % maxlen== Head（队尾指针的下一个位置是队头，利用预留空位区分队满 / 队空）。
队列容量maxlen ：数组的总长度（为了区分 "队满" 和 "队空"，通常会预留 1 个空位，实际可存储元素数 = maxlen-1）

3.指针移动规则

无论是入队（Tail 后移）还是出队（Head 后移），都通过取模 % maxlen实现循环：

入队后：Tail = (Tail + 1) % maxlen；
出队后：Head = (Head + 1) % maxlen

示例：

头文件：

cpp 复制代码

#ifndef _SEQQUEUE_H
#define _SEQQUEUE_H

typedef int DataType;

typedef struct seqque
{
    DataType *pData;
    int Head;
    int Tail;
    int Maxlen;
}seqqueue_t;

extern seqqueue_t *CreateSeqQueue(int len);
extern int IsEmptySeqQueue(seqqueue_t *pTmpQueue);
extern int IsFullSeqQueue(seqqueue_t *pTmpQueue);
extern int EnterSeqQueue(seqqueue_t *pTmpQueue, DataType TmpData);
extern DataType QuitSeqQueue(seqqueue_t *pTmpQueue);
extern int DestorySeqQueue(seqqueue_t **ppTmpQueue);

#endif

函数：

cpp 复制代码

#include<stdio.h>
#include<stdlib.h>
#include"seqqueue.h"

seqqueue_t *CreateSeqQueue(int len)
{
    seqqueue_t *pNewNode = NULL;

//    DataType *pTmpNode = NULL;
    
    pNewNode = malloc(sizeof(seqqueue_t));
    if(pNewNode == NULL)
    {
        perror("fail to malloc");
        return NULL;
    }
#if 0
    pTmpNode = malloc(len * (sizeof(DataType)));
    if(pTmpNode == NULL)
    {
        perror("fail to malloc");
        return NULL;
    }
#endif

//    pNewNode->pData = pTmpNode;
    
    pNewNode->Head = 0;
    pNewNode->Tail = 0;
    pNewNode->Maxlen = len;
    pNewNode->pData = malloc(sizeof(DataType) * len);
    if(pNewNode->pData == NULL)
    {
        perror("fail to malloc");
        return NULL;
    }
   
    return pNewNode;
}

int IsEmptySeqQueue(seqqueue_t *pTmpQueue)
{
    return pTmpQueue->Head == pTmpQueue->Tail ? 1 : 0;
}

int IsFullSeqQueue(seqqueue_t *pTmpQueue)
{
    return ((pTmpQueue->Tail + 1) % pTmpQueue->Maxlen == pTmpQueue->Head) ? 1 : 0;
}

int EnterSeqQueue(seqqueue_t *pTmpQueue, DataType TmpData)
{
    if(IsFullSeqQueue(pTmpQueue))
    {
        return -1;
    }

    pTmpQueue->pData[pTmpQueue->Tail] = TmpData;//从队尾开始入列
    pTmpQueue->Tail = (pTmpQueue->Tail+1) % pTmpQueue->Maxlen;//尾向后走，走到最后一个回到开头

    return 0;
}

DataType QuitSeqQueue(seqqueue_t *pTmpQueue)
{
    DataType TmpData;

    if(IsEmptySeqQueue(pTmpQueue))
    {
        return -1;
    }

    TmpData = pTmpQueue->pData[pTmpQueue->Head];
    pTmpQueue->Head = (pTmpQueue->Head + 1) % pTmpQueue->Maxlen;

    return TmpData;
}

int DestorySeqQueue(seqqueue_t **ppTmpQueue)
{
    free((*ppTmpQueue)->pData);
    free(*ppTmpQueue);
    *ppTmpQueue = NULL;

    return 0;
}

主函数：

cpp 复制代码

#include<stdio.h>
#include<stdlib.h>
#include"seqqueue.h"

int main(void)
{
    seqqueue_t *pseqqueue = NULL;
    int i = 0;

    pseqqueue = CreateSeqQueue(10);

    while(!IsFullSeqQueue(pseqqueue))
    {
        EnterSeqQueue(pseqqueue, i);
        i++;
    }

    while(!IsEmptySeqQueue(pseqqueue))
    {
        printf("%d ", QuitSeqQueue(pseqqueue));
    }
    printf("\n");

    DestorySeqQueue(&pseqqueue);

    return 0;
}

2.链式队列

核心是利用单向链表尾插法入队

入队：新建节点，让尾指针的next指向新节点，再将尾指针移到新节点（空队列时头、尾指针同时指向新节点）；
出队：保存头节点的数，将头指针移到下一个节点（出队后为空时，尾指针也要置空），再返回保存的数；
仅需判空，无需判满（链表可动态新增节点，理论上仅受内存限制）

示例：

头文件：

cpp 复制代码

#ifndef _LINKQUEUE_H
#define _LINKQUEUE_H

typedef int DataType;

typedef struct node
{
    DataType Data;
    struct node *pNext;
}Node_t;

extern Node_t *CreatEmptyLinkQueue(void);

extern int IsEmptyLinkQueue(Node_t *pHead);

extern int EnterLinkQueue(Node_t *pHead, DataType TmpData);

extern DataType QuitLinkQueue(Node_t *pHead);

extern int DestoryLinkQueue(Node_t **ppHead);

#endif

函数：

cpp 复制代码

#include<stdio.h>
#include<stdlib.h>
#include"linkqueue.h"

Node_t *CreatEmptyLinkQueue(void)
{
    Node_t *pNewNode = NULL;

    pNewNode = malloc(sizeof(Node_t));
    if(pNewNode == NULL)
    {
        perror("fail to malloc");
        return NULL;
    }

    pNewNode->pNext = NULL;

    return pNewNode;
}

int IsEmptyLinkQueue(Node_t *pHead)
{
    return pHead->pNext == NULL ? 1 : 0;
}

int EnterLinkQueue(Node_t *pHead, DataType TmpData)
{
    Node_t *pNewNode = NULL;
    Node_t *pLastQueue = NULL;

    pNewNode = malloc(sizeof(Node_t));
    if(pNewNode == NULL)
    {
        perror("fail to malloc");
        return -1;
    }

    pNewNode->Data = TmpData;
    pNewNode->pNext = NULL;

    pLastQueue = pHead;
    while(pLastQueue->pNext != NULL)
    {
        pLastQueue = pLastQueue->pNext;
    }

    pLastQueue->pNext = pNewNode;

    return 0;
}

DataType QuitLinkQueue(Node_t *pHead)
{
    Node_t *pTmpQueue = NULL;
    DataType TmpData;

    if(IsEmptyLinkQueue(pHead))
    {
        return 0;
    }

    pTmpQueue = pHead->pNext;
    TmpData = pTmpQueue->Data;
    pHead->pNext = pTmpQueue->pNext;
    free(pTmpQueue);
    pTmpQueue = NULL;

    return TmpData;
}

int DestoryLinkQueue(Node_t **ppHead)
{
    Node_t *pTmpQueue = NULL;
    Node_t *pFreeQueue = NULL;

    pTmpQueue = pFreeQueue = *ppHead;
    while(pTmpQueue != NULL)
    {
        pTmpQueue = pTmpQueue->pNext;
        free(pFreeQueue);
        pFreeQueue = pTmpQueue;
    }

    *p

主函数：

cpp 复制代码

#include<stdio.h>
#include"linkqueue.h"

int main(void)
{
    Node_t *plinkqueue = NULL;

    plinkqueue = CreatEmptyLinkQueue();

    EnterLinkQueue(plinkqueue, 1);
    EnterLinkQueue(plinkqueue, 2);
    EnterLinkQueue(plinkqueue, 3);
    EnterLinkQueue(plinkqueue, 4);
    EnterLinkQueue(plinkqueue, 5);

    while(!IsEmptyLinkQueue(plinkqueue))
    {
        printf("%d ", QuitLinkQueue(plinkqueue));
    }
    printf("\n");
    
    DestoryLinkQueue(&plinkqueue);

    return 0;
}

二、二叉树

1.概念

树：描述数据一对多关系的数据结构；
前驱：数据从哪来；
后继：数据对应后续的节点；
节点：二叉树的基本单元，包含数据域 （存值）、左孩子指针 （指向左子节点）、右孩子指针（指向右子节点）；
根节点：最顶层节点，没有前驱只有后继；
叶子节点：只有前驱没有后继；
分支节点：既有前驱又有后继；
**层：**根节点所在的位置称为第一层，每过一个节点层数+1；
树的高度：距离该节点最远的叶子节点的距离；
树的深度：距离根节点的节点个数；
度：前驱或者后继的个数
- 入度：均为1；
- 出度：后继节点的个数；

2.二叉树

树形结构中每个节点最多有两个后继节点；
满二叉树 ：除叶子节点外，每个节点都有两个子节点，且所有叶子节点在同一层；
完全二叉树 ：按层序（从上到下、从左到右）编号，所有节点的编号和同深度的满二叉树完全一致（叶子节点只出现在最后两层，且最后一层的叶子都靠左）。
- 右孩子：二叉树中节点左侧的子节点；
- 左孩子：二叉树中节点右侧的子节点；
二叉树特性：
- 第k层最多有：2^(k-1) 个节点
- 前k层最多有：2^k -1 个节点
二叉树的遍历：
- 深度优先遍历：DFS
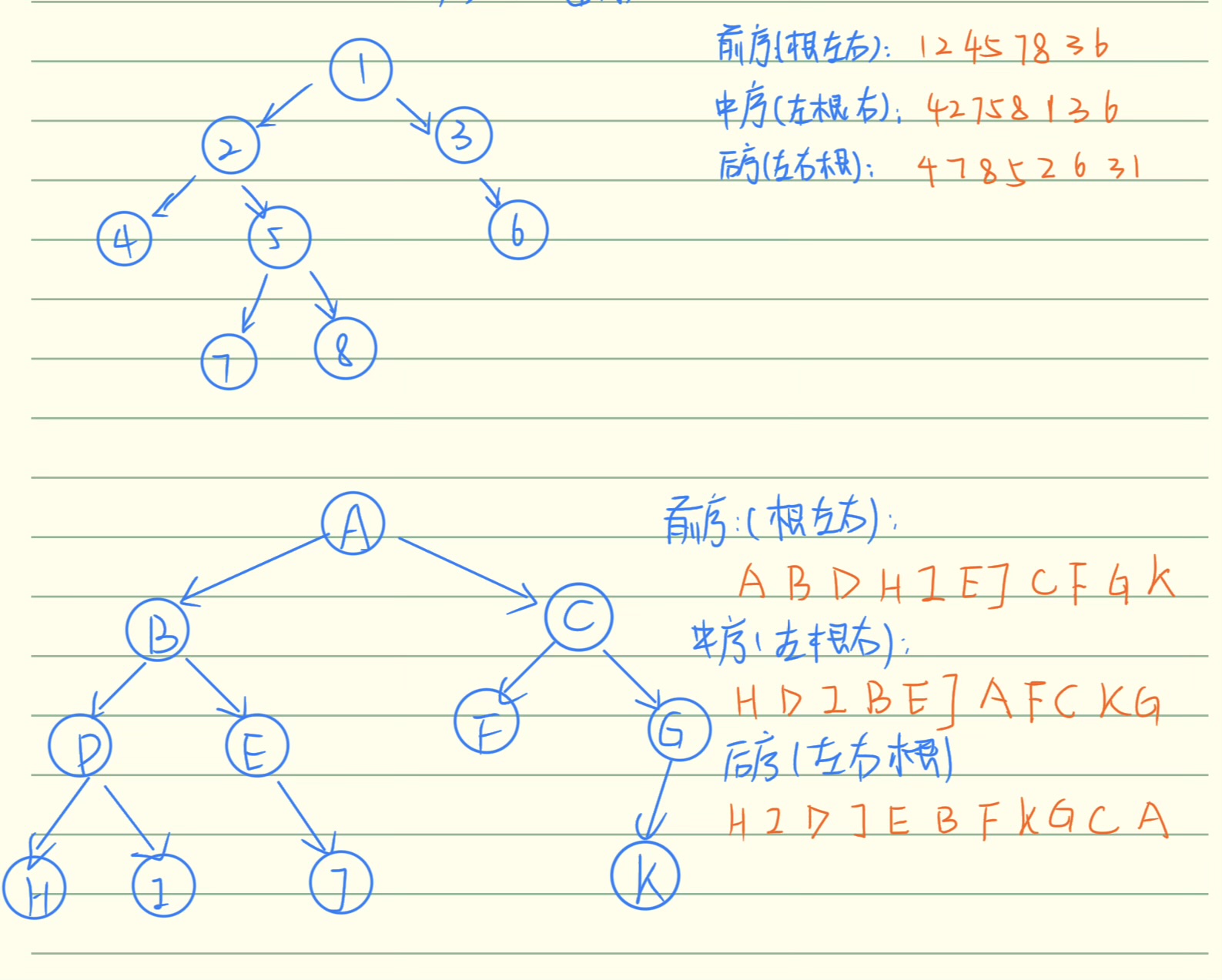
  - 前序遍历：根左右，先访问根节点 → 递归遍历左子树 → 递归遍历右子树
  - 中序遍历：左根右，先递归遍历左子树 → 访问根节点 → 递归遍历右子树
  - 后续遍历：左右根，先递归遍历左子树 → 递归遍历右子树 → 访问根节点

广度优先遍历：BFS
- 层序遍历：每层从左到右遍历