P1880 [NOI1995] 石子合并
题目描述
在一个圆形操场的四周摆放 N N N 堆石子,现要将石子有次序地合并成一堆,规定每次只能选相邻的 2 2 2 堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分。
试设计出一个算法,计算出将 N N N 堆石子合并成 1 1 1 堆的最小得分和最大得分。
输入格式
数据的第 1 1 1 行是正整数 N N N,表示有 N N N 堆石子。
第 2 2 2 行有 N N N 个整数,第 i i i 个整数 a i a_i ai 表示第 i i i 堆石子的个数。
输出格式
输出共 2 2 2 行,第 1 1 1 行为最小得分,第 2 2 2 行为最大得分。
输入输出样例 #1
输入 #1
4
4 5 9 4输出 #1
43
54说明/提示
1 ≤ N ≤ 100 1\leq N\leq 100 1≤N≤100, 0 ≤ a i ≤ 20 0\leq a_i\leq 20 0≤ai≤20。
题意分析
1.规定每次只能选相邻的 2 堆合并成新的一堆
这就非常明了了,必须相邻2堆合并
2.将石子有次序地合并成一堆
这就是多余的,会误导理解,理解成从左往右或从右往左按序合并。 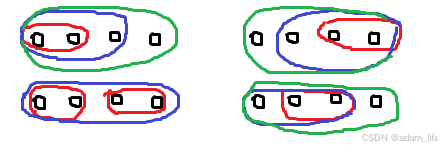
3."相邻的 2 堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分"------"将 N 堆石子合并成 1 堆的"总得分。例1、2、3=第一次合并s(1,2)+第二次合并s(s(1,2)+3)。
4.只有1个堆的合并和是0,只有2个堆的只能选相邻两,三个以上就要比较选择

代码
cpp
#include <bits/stdc++.h>
using namespace std;
const int N=205;
const int inf=0x3f3f3f3f;
int n,
x,
d[N],//各石子堆石子数
s[N],//环变线后前缀和
dpmin[N][N],//从第几堆到第几堆全部"合并"后的最小得分
dpmax[N][N];//从第几堆到第几堆全部"合并"后的最大得分
int main(){
freopen("data.cpp","r",stdin);
cin>>n;
for(int i=1;i<=n;i++){//遍历每个石堆
cin>>x;d[i]=d[n+i]=x;//n个环形石堆变成2*n个线性石堆
}
for(int i=1;i<=2*n;i++)s[i]=s[i-1]+d[i];//到第i石堆的石子总数
//for(int i=1;i<=2*n;i++)dpmin[i][i]=dpmax[i][i]=0;//原石堆不经合并,所以没有合并数
for(int len=2;len<=n;len++)//区间宽度,原石堆合并数为0,可直求2石堆合并数,再比较求3石堆合并数(如1和2+3,或1+2和3),依此类推
for(int l=1;l+len-1<=2*n;l++){//该区间始发位置l
int r=l+len-1;//区间右界
dpmin[l][r]=inf,dpmax[l][r]=0;//本次求len宽度区间的值
for(int m=l;m<r;m++){//拆分该区间
dpmin[l][r]=min(dpmin[l][r],dpmin[l][m]+dpmin[m+1][r]+s[r]-s[l-1]);//两次得分的和
dpmax[l][r]=max(dpmax[l][r],dpmax[l][m]+dpmax[m+1][r]+s[r]-s[l-1]);
}
}
int ansmin=inf,ansmax=0;//最小和最大值
for(int i=1;i<=n;i++){
ansmin=min(ansmin,dpmin[i][i+n-1]),ansmax=max(ansmax,dpmax[i][i+n-1]);//n宽区间的最优值
}
cout<<ansmin<<endl<<ansmax;
return 0;
}