【C++】AVL树 - 技术栈

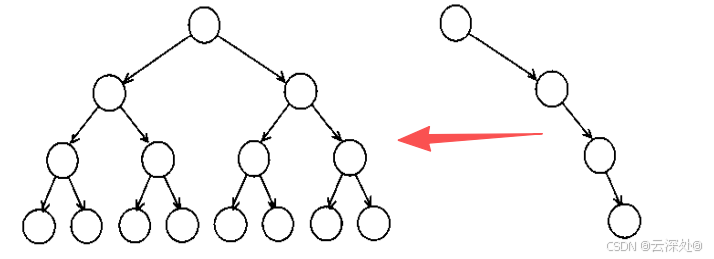
由于插入值不随机，或者某种极端情况，二叉搜索树会退化至链表。因此需要引入平衡搜索树的概念，而平衡搜索树分为AVL-Tree，RB-Tree，AA-Tree，处于平衡状态的树在搜索和插入删除的时间复杂度会相对减少

一.AVL树概念

AVL树是加上平衡条件的二叉搜索树，保证每个节点的左右子树高度差的绝对值不超过1，则可以降低树的高度，减少平均搜索长度，保证整棵树的深度为logN，我们这里规定平衡因子的值为右树数量最大-左树数量最大

平衡因子的维护：

新增cur在parent的左，平衡因子--

新增cur在parent的右，平衡因子++

更新后parent的平衡因子为0，树处于平衡状态，返回

更新后parent的平衡因子为+(-)1，parent树的高度变化，需要继续向上维护平衡因子，直到parent的平衡因子为0

更新后parent的平衡因子为+(-)2，parent树的高度变化且不平衡，需要对该树旋转

旋转：旋转后保持树为搜索树，且降低子树的高度

二.AVL树的插入

插入点位于parent的左节点的左子树-左左---对gparent右旋
插入点位于parent的左节点的右子树-左右---对cur左旋，parent右旋
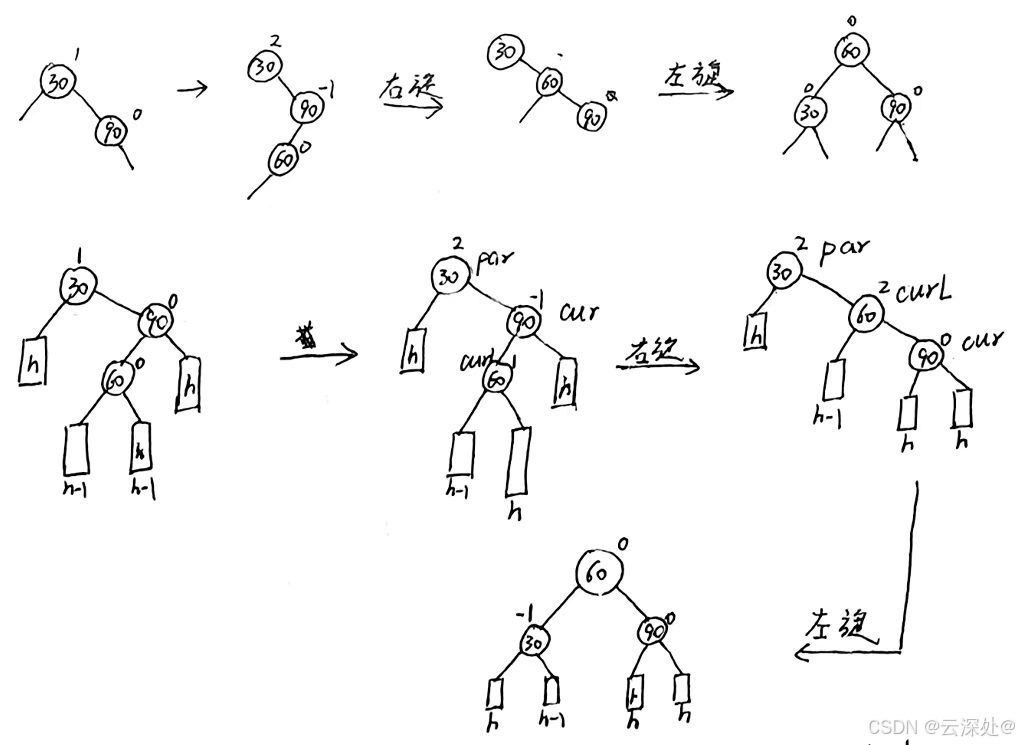
插入点位于parent的右节点的左子树-右左---对cur右旋，curl左旋
插入点位于parent的右子树的右子树-右右---对gparent左旋

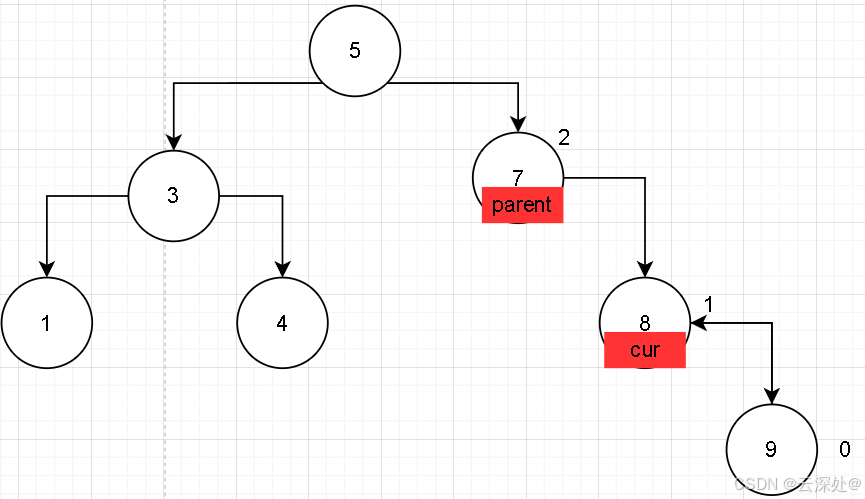
右右：

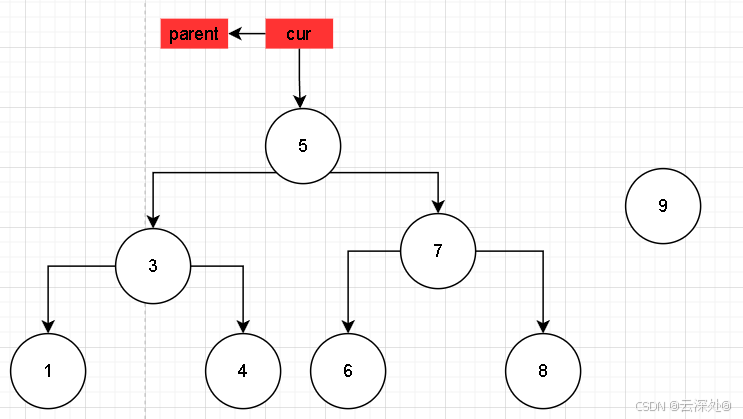
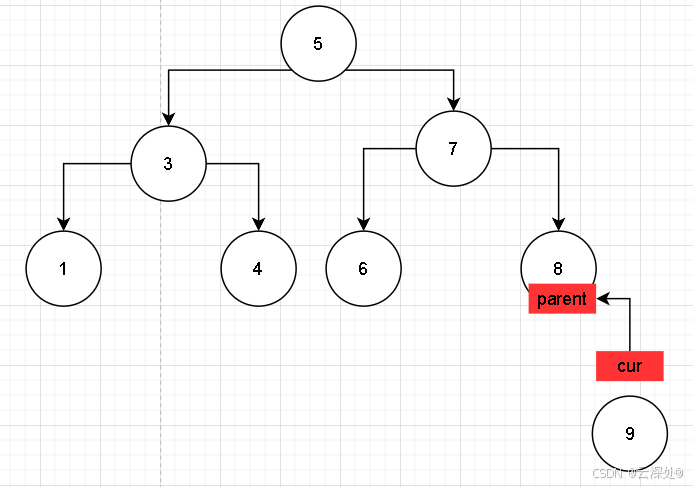
当插入9时，cur记录当前节点，parent记录父节点，便于建立双向链接

当寻找逻辑结束，cur指向应该插入的位置，且此时指向nullptr，需要通过传入的kv创建对象

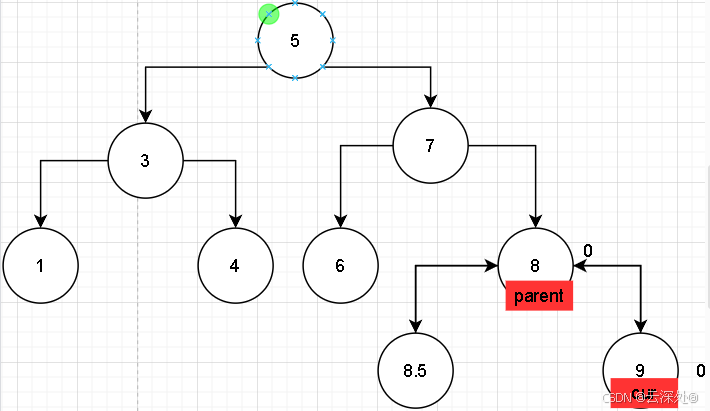
情景1：若插入后，8节点的左右节点个数相等，_bf设置为0，插入节点成功，不需要改变_bf，直接返回

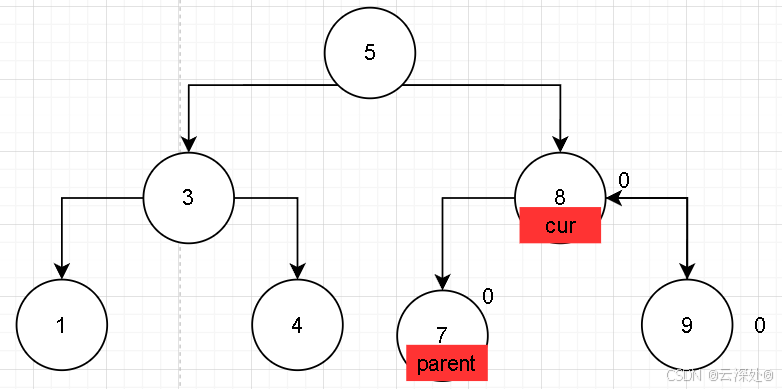
情景2：当需要改变时，cur和parent集体上移一格，parent指向要的改变节点，将这个节点的值由1改为2，此时出现不平衡，需要对parent进行左旋（即插入节点的gparent）

将cur，parent的平衡因子该为0

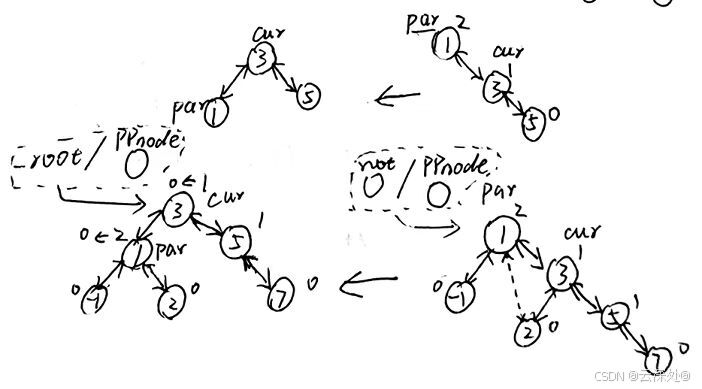
左左：

讨论root为空和不为空+右旋

cur和parent的平衡因子设为0

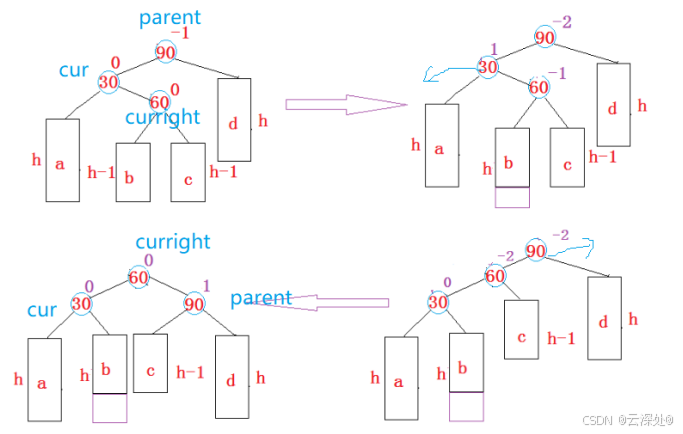
右左：

左右：

三.AVL的实现

节点定义

cpp 复制代码

struct AVLTreeNode
{	
	pair<K, V> _kv;
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;
	int _bf;

	AVLTreeNode(const pair<K, V>& kv) :_left(nullptr), _right(nullptr), _parent(nullptr), _bf(0), _kv(kv)
	{}
};

insert实现

cpp 复制代码

bool insert(const pair<K, V>& kv)
{
	if (_root == nullptr)
	{
		_root = new Node(kv);
			return true;	//根节点为空创建节点
	}
	Node* cur = _root;
	Node* parent = nullptr;
	while (cur)		//通过key值比较寻找插入点
	{
		if (kv.first > cur->_kv.first)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (kv.first < cur->_kv.first)
		{
			parent = cur;
			cur = cur->_left;
		}
		else return false;		//当存在重复元素，返回false
	}
	cur = new Node(kv);
	//比较parent的key，确定node的位置
	if (kv.first > parent->_kv.first)
	{
		parent->_right = cur;
	}
	else parent->_left = cur;

	cur->_parent = parent;		//更新双向链接

	while (parent)	//自下向上更新平衡因子，_bf = 右边个数-左边个数
	{
		if (parent->_left == cur) parent->_bf--;		//改变_bf的逻辑
		else parent->_bf++;

		//分类讨论_bf是否向上更新，需要更新则改变parent,cur的指向
		if (parent->_bf == 0) break;
		else if (parent->_bf == 1 || parent->_bf == -1)
		{
			cur = parent;
			parent = parent->_parent;
		}
		else if (parent->_bf == 2 || parent->_bf == -2)
		{
			//旋转逻辑
			if (parent->_bf == 2 && cur->_bf == 1)		//右边节点数量多,左旋
			{
				RotateL(parent);	//旋转+修改平衡因子
			}
			else if (parent->_bf == -2 && cur->_bf == -1)
			{
				RotateR(parent);
			}
			else if (parent->_bf == 2 && cur->_bf == -1)
			{
				RotateRL(parent);
			}
			else if (parent->_bf == -2 && cur->_bf == 1)
			{
				RotateLR(parent);
			}
			break;
		}
		else assert(false);	//确保发现混乱，_bf的值出错
	}
	return true;
}

左旋实现

cpp 复制代码

void RotateL(Node* parent)
{
	Node* cur = parent->_right;
	Node* cur_left = cur->_left;
	
	parent->_right = cur_left;
	if (cur_left) cur_left->_parent = parent;

	cur->_left = parent;
	Node* ppnode = parent->_parent;		//保存parent的父节点，链接cur
	parent->_parent = cur;		//变成cur的左节点

	if (parent == _root)	//讨论根节点
	{
		_root = cur;
		cur->_parent = nullptr;
	}
	else
	{
		if (ppnode->_left == parent) ppnode->_left = cur;
		else ppnode->_right = cur;

		cur->_parent = ppnode;
	}
	parent->_bf = cur->_bf = 0;		//更新_bf的值
}

右旋

cpp 复制代码

void RotateR(Node* parent)
{
	Node* cur = parent->_left;
	Node* cur_right = cur->_right;

	parent->_left = cur_right;
	if (cur_right) cur_right->_parent = parent;

	cur->_right = parent;
	Node* ppnode = parent->_parent;
	parent->_parent = cur;

	if (parent == _root)
	{
		_root = cur;
		cur->_parent = nullptr;
	}
	else
	{
		if (ppnode->_left == parent) ppnode->_left = cur;
		else ppnode->_right = cur;
	}
	cur->_bf = parent->_bf = 0;
}

双旋

cpp 复制代码

void RotateRL(Node* parent)
{
	Node* cur = parent->_right;
	Node* cur_left = cur->_left;
	int bf = cur_left->_bf;

	RotateR(parent->_right);
	RotateL(parent);
	//更新平衡因子
	if (bf == 0)
	{
		parent->_bf = 0;
		cur->_bf = 0;
		cur_left->_bf = 0;
	}
	else if (bf == 1)
	{
		parent->_bf = -1;
		cur->_bf = 0;
		cur_left->_bf = 0;
	}
	else if (bf == -1)
	{
		parent->_bf = 0;
		cur->_bf = 1;
		cur_left->_bf = 0;
	}
	else assert(false);
}

void RotateLR(Node* parent)
{
	Node* cur = parent->_left;
	Node* cur_right = cur->_right;
	int bf = cur_right->_bf;

	RotateR(parent->_left);
	RotateL(parent);
	//更新平衡因子
	if (bf == 0)
	{
		parent->_bf = 0;
		cur->_bf = 0;
		cur_right->_bf = 0;
	}
	else if (bf == 1)
	{
		parent->_bf = 0;
		cur->_bf = -1;
		cur_right->_bf = 0;
	}
	else if (bf == -1)
	{
		parent->_bf = 1;
		cur->_bf = 0;
		cur_right->_bf = 0;
	}
	else assert(false);
}