基于樽海鞘算法（SSA）的极限学习机（ELM）回归预测对比：BP、GRNN、ELM与SSA - ELM

基于樽海鞘算法（SSA）的极限学习机（ELM）回归预测与BP、GRNN、ELM比较--matlab 通过BP、GRNN、ELM、SSA-ELM对样本数据进行回归预测，SSA-ELM优于ELM>GRNN>BP 适应度函数选取以训练集的误差MSE。

在机器学习的预测领域，回归预测是一项至关重要的任务。今天咱们就来聊聊基于樽海鞘算法（SSA）优化的极限学习机（ELM）回归预测，并与传统的BP神经网络、广义回归神经网络（GRNN）以及未优化的ELM进行一番比较，而且是以MATLAB为工具展开哦。

1. 算法概述

1.1 极限学习机（ELM）

ELM是一种单隐层前馈神经网络，其独特之处在于随机生成输入层与隐藏层之间的连接权重以及隐藏层神经元的阈值，只需计算输出权重，训练速度极快。简单的ELM模型代码示例如下：

matlab 复制代码

% 生成随机数据作为示例
n = 100; % 数据点数量
x = linspace(0, 10, n);
y = 2 * x + 1 + 0.5 * randn(size(x)); % 带噪声的线性关系

% 划分训练集和测试集
train_ratio = 0.7;
train_idx = 1:round(train_ratio * n);
test_idx = (round(train_ratio * n)+1):n;

X_train = x(train_idx);
Y_train = y(train_idx);
X_test = x(test_idx);
Y_test = y(test_idx);

% 设置ELM参数
hidden_neurons = 10; % 隐藏层神经元数量

% 训练ELM
input_weights = rand(hidden_neurons, 1);
bias = rand(hidden_neurons, 1);
H = sigmoid(input_weights * X_train + bias); % 计算隐藏层输出
beta = pinv(H) * Y_train'; % 计算输出权重

% 预测
H_test = sigmoid(input_weights * X_test + bias);
Y_pred = beta' * H_test;

这里我们先生成了一些简单的模拟数据，划分训练集和测试集后，随机初始化输入权重和偏置，通过计算隐藏层输出进而求出输出权重，完成训练过程，最后进行预测。

1.2 樽海鞘算法（SSA）优化ELM

SSA模拟了樽海鞘群体的觅食行为。将其用于优化ELM时，主要是优化ELM的输入权重和隐藏层阈值，使得模型性能更好。这里假设使用SSA优化上述ELM的输入权重和偏置，伪代码如下：

matlab 复制代码

% SSA参数设置
pop_size = 30; % 种群数量
max_iter = 100; % 最大迭代次数

% 初始化樽海鞘种群位置（对应ELM的输入权重和偏置）
Positions = rand(hidden_neurons + 1, pop_size);

for t = 1:max_iter
    % 计算适应度值（这里以训练集MSE作为适应度函数）
    fitness = zeros(1, pop_size);
    for i = 1:pop_size
        input_weights = Positions(1:hidden_neurons, i);
        bias = Positions(hidden_neurons+1, i);
        H = sigmoid(input_weights * X_train + bias);
        beta = pinv(H) * Y_train';
        H_test = sigmoid(input_weights * X_test + bias);
        Y_pred = beta' * H_test;
        fitness(i) = mean((Y_pred - Y_test).^2);
    end

    % 更新樽海鞘位置
    % 这里省略具体更新公式，实际代码需按照SSA原理实现
    % ......
    Positions = new_Positions; % 更新后的位置
end

% 使用最优位置对应的参数训练ELM
best_idx = find(fitness == min(fitness));
best_input_weights = Positions(1:hidden_neurons, best_idx);
best_bias = Positions(hidden_neurons+1, best_idx);
H = sigmoid(best_input_weights * X_train + best_bias);
beta = pinv(H) * Y_train';
H_test = sigmoid(best_input_weights * X_test + best_bias);
Y_pred_SSA_ELM = beta' * H_test;

在这个过程中，通过不断迭代更新樽海鞘的位置（对应ELM的关键参数），以训练集均方误差（MSE）作为适应度函数，找到最优的参数组合来提升ELM性能。

1.3 BP神经网络

BP神经网络通过反向传播算法不断调整网络的权重和阈值，以最小化误差。MATLAB中实现简单BP神经网络回归预测代码如下：

matlab 复制代码

net = feedforwardnet(10); % 创建含10个隐藏层神经元的BP网络
net = train(net, X_train', Y_train'); % 训练网络
Y_pred_BP = net(X_test'); % 预测

这里直接使用MATLAB自带的神经网络工具箱，创建并训练BP网络，虽然简单，但实际应用中可能需要更多超参数调整。

1.4 广义回归神经网络（GRNN）

GRNN基于非线性回归理论，对样本数据的拟合能力较强。MATLAB实现代码示例：

matlab 复制代码

net = newgrnn(X_train', Y_train', 0.1); % 创建GRNN网络，spread参数设为0.1
Y_pred_GRNN = net(X_test'); % 预测

GRNN的关键在于spread参数的设置，它影响着网络的泛化能力。

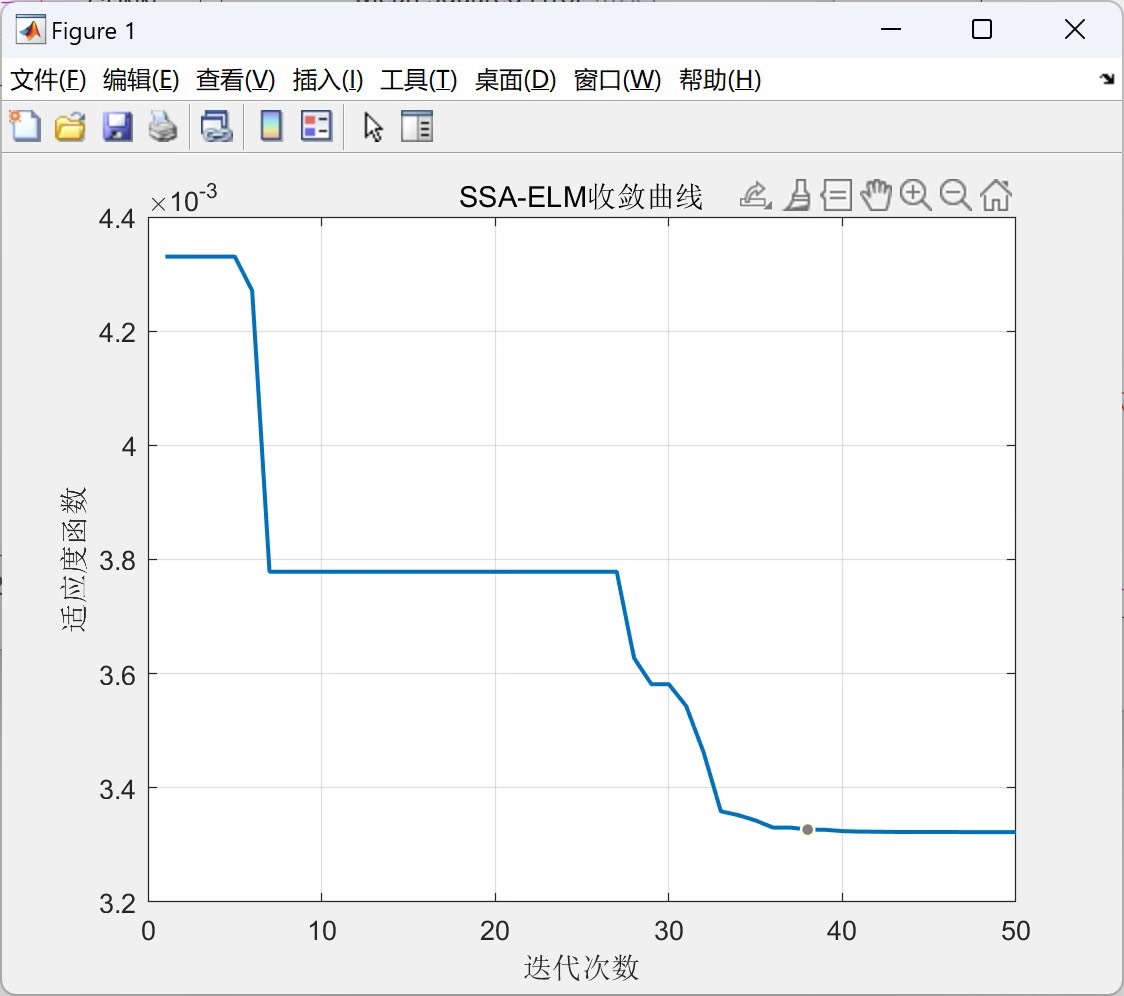
2. 性能比较

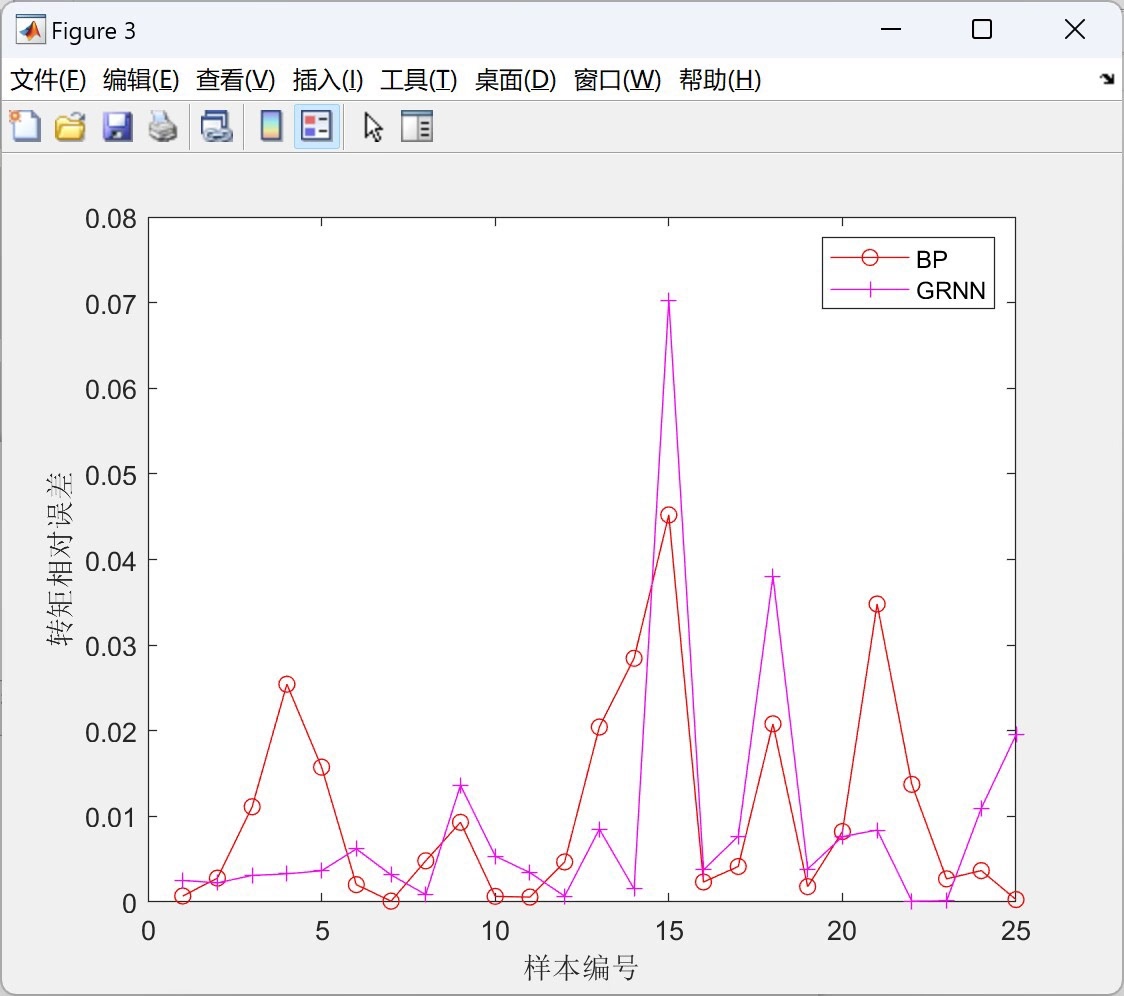
文中提到适应度函数选取训练集的误差MSE，最终结果是SSA - ELM优于ELM > GRNN > BP。从实际意义来讲，SSA - ELM通过樽海鞘算法优化了ELM的关键参数，使得模型在训练集上的误差更小，泛化能力也可能更强。而ELM本身训练速度快，但可能因随机初始化参数导致结果不稳定，SSA优化后改善了这一问题。GRNN对数据的局部拟合能力不错，但整体性能稍逊于优化后的ELM。BP神经网络虽然经典，但训练速度慢且容易陷入局部最优，导致在这个比较中表现相对较差。

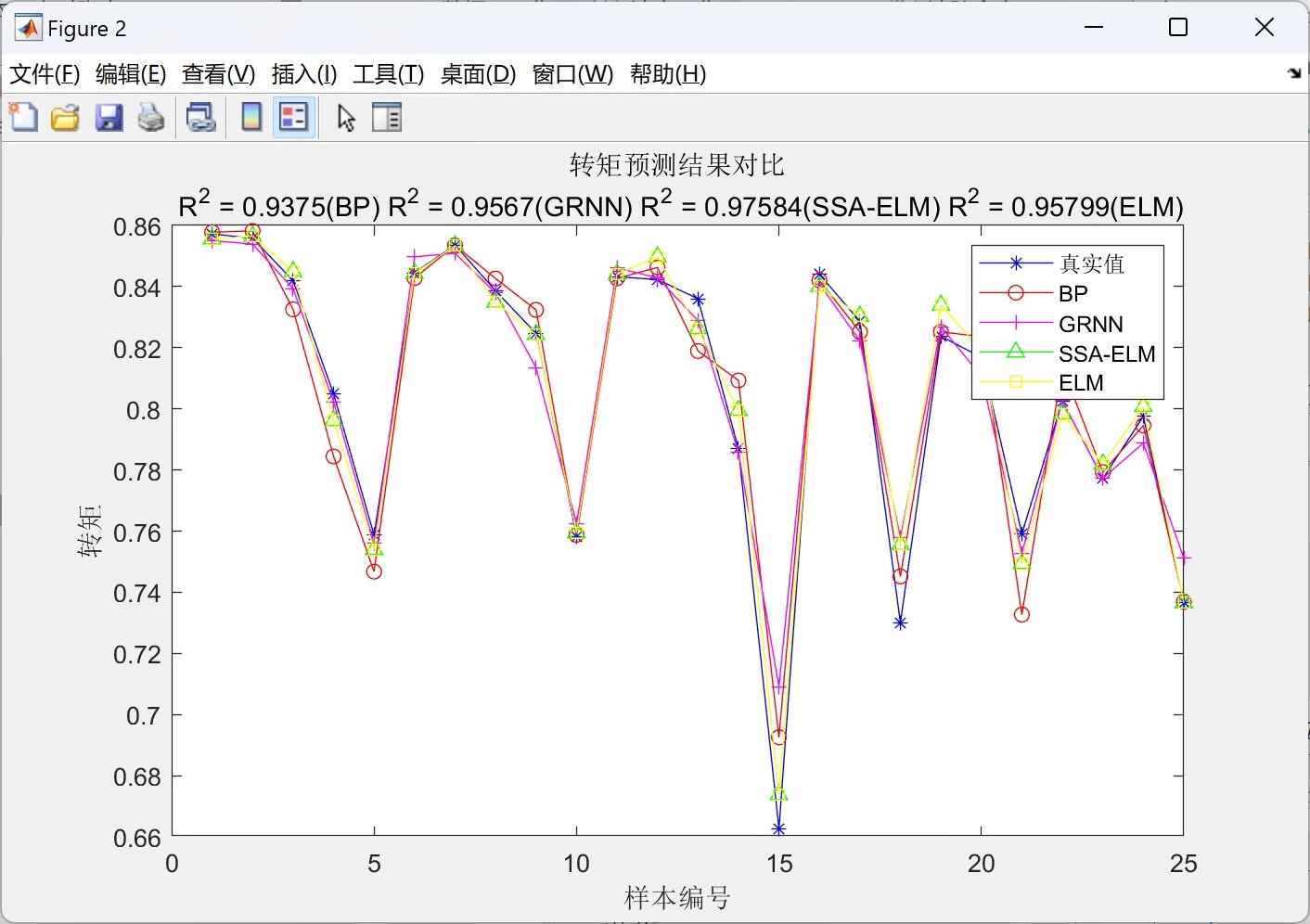
综上所述，在回归预测任务中，基于樽海鞘算法优化的极限学习机展现出了一定优势，为实际应用提供了一种更有效的选择。当然，具体问题还需具体分析，不同数据集和场景下各算法表现可能会有所不同。