MATLAB 中基于最大重叠离散小波变换的心电信号处理探索

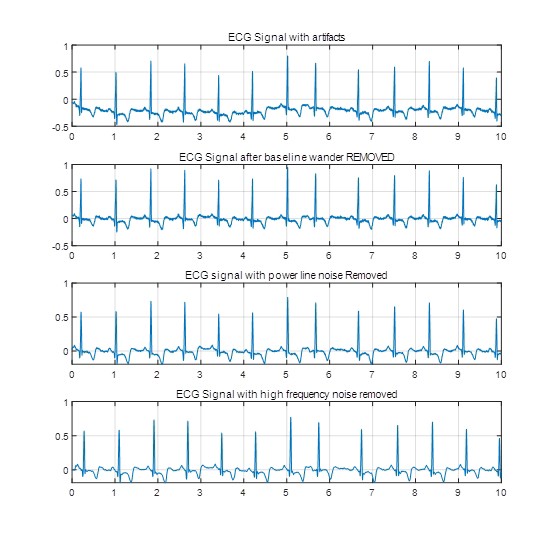
MATLAB环境下基于最大离散重叠离散小波变换的心电信号ECG信号处理（删除伪影，滤波降噪，检测ECG信号的PQRST波并确定患者的心跳）算法运行环境为MATLAB R2018a，采用最大重叠离散小波变换对ECG信号进行处理，包括删除伪影，滤波降噪，检测ECG信号的PQRST波并确定患者的心跳等。算法可迁移至金融时间序列，地震信号，语音信号，声信号，生理信号（ECG,EEG,EMG）等一维时间序列信号。

在生物医学信号处理领域，心电信号（ECG）的准确分析至关重要。今天咱们就来聊聊在 MATLAB R2018a 环境下，利用最大重叠离散小波变换对 ECG 信号进行一系列处理的奇妙之旅。

一、最大重叠离散小波变换（MODWT）简介

最大重叠离散小波变换是一种强大的信号处理工具。相比于传统的离散小波变换，它具有平移不变性，这对于处理像 ECG 这样的生理信号特别有用，因为生理信号中的微小移位可能会导致特征提取的巨大差异。

二、ECG 信号处理流程

删除伪影
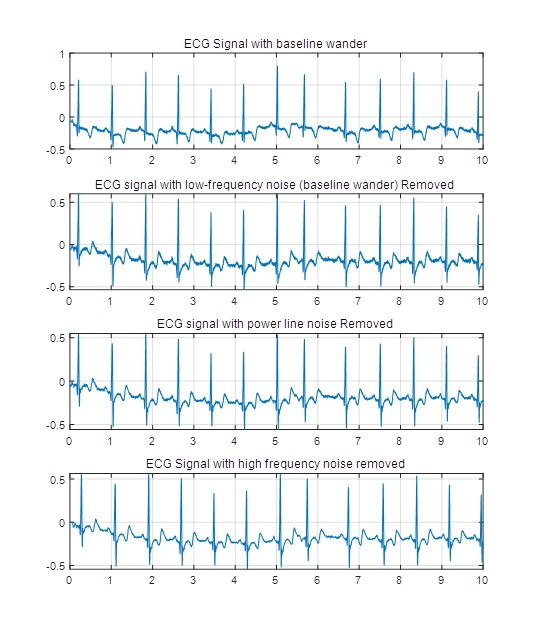
在实际采集的 ECG 信号中，经常会混入各种伪影，这些伪影可能来自电极接触不良、肌肉运动干扰等。通过 MODWT，可以有效地将这些伪影从原始信号中分离出来。
matlab
% 假设已经读取了ECG信号存储在变量ecgsignal中
% 对信号进行MODWT分解
[C, L] = modwt(ecg signal, 'db4', 5);
% 'db4'是选用的小波基，5是分解层数
% 分析系数，找到代表伪影的系数层
% 这里简单假设第5层系数主要包含伪影（实际可能需更复杂分析）
C(:,5) = 0;
% 重构信号，去除伪影
cleanecg signal = imodwt(C, L, 'db4');

代码分析：首先使用 modwt 函数对原始 ECG 信号进行分解，这里选择了 db4 小波基和 5 层分解。然后通过分析系数，将我们认为主要包含伪影的第 5 层系数置零。最后利用 imodwt 函数进行信号重构，得到去除伪影后的干净 ECG 信号。

滤波降噪
尽管去除了伪影，信号中仍可能存在噪声。MODWT 同样可以用于滤波降噪。
matlab
% 对去除伪影后的信号进行降噪
[Cnoise, L noise] = modwt(cleanecg signal, 'db4', 5);
% 设定阈值，这里简单用一个经验值（实际需调整）
threshold = 0.5;
Cnoise filt = wthresh(Cnoise, 'h', threshold);
% 软阈值处理
denoised ecgsignal = imodwt(C noisefilt, L noise, 'db4');

代码分析：对去除伪影后的信号再次进行 MODWT 分解。设定一个阈值，这里用了一个简单的经验值 0.5，然后通过 wthresh 函数对系数进行软阈值处理，去除噪声相关的系数。最后重构信号，得到降噪后的 ECG 信号。

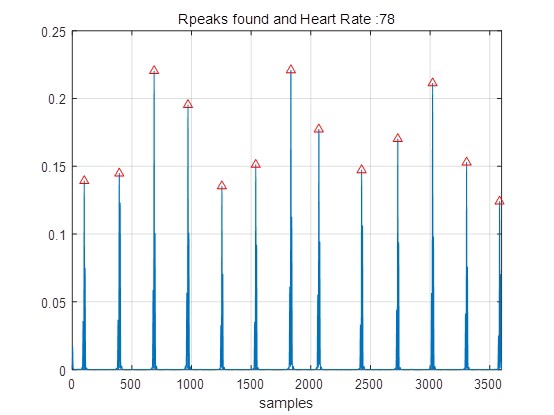
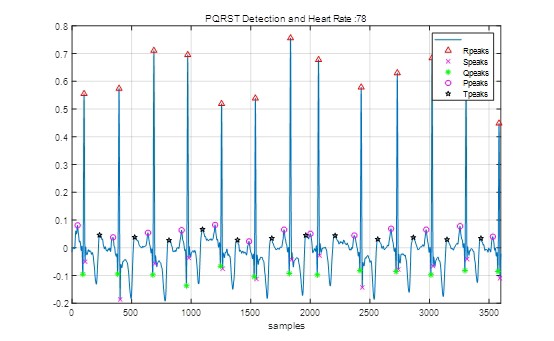
检测 ECG 信号的 PQRST 波并确定心跳
检测 PQRST 波是分析 ECG 信号的关键步骤，而确定心跳则是基于这些波的检测结果。
matlab
% 利用降噪后的信号检测R波（假设已存在检测R波的函数detectR wave）
[Rpeaks, R locs] = detectR wave(denoisedecg signal);
% 根据R波位置计算心跳
heartrate = 60 / mean(diff(R locs));
% 这里简单计算心跳，实际可能需更复杂算法
% 后续可以利用类似方法检测P, Q, S, T波（代码此处省略）

代码分析：首先调用一个假设存在的 detectRwave 函数来检测 R 波及其位置。然后根据 R 波位置的时间间隔计算心跳频率。实际应用中，检测 P、Q、S、T 波可能需要更复杂的算法和处理，但基本思路类似。

三、算法的可迁移性

这种基于 MODWT 的处理算法不仅仅局限于 ECG 信号。它可以迁移至金融时间序列，帮助分析股票价格走势等；在地震信号处理中，用于分析地震波特征；对于语音信号、声信号以及其他生理信号（如 EEG、EMG）等一维时间序列信号都有着潜在的应用价值。因为这些信号都具有时间序列的特性，MODWT 的平移不变性和多分辨率分析能力在这些领域同样能发挥重要作用。

总之，基于最大重叠离散小波变换的 ECG 信号处理算法在 MATLAB 环境下展现出了强大的功能，无论是对生物医学研究还是其他涉及一维时间序列信号处理的领域，都有着广阔的应用前景。希望大家可以尝试将这个算法应用到自己感兴趣的领域，挖掘更多的可能性。