基于熵权法和灰色关联分析的综合评价算法MATLAB代码

一、研究背景

随着金融行业竞争的加剧和监管要求的提高，对银行机构进行科学、客观、全面的综合评价显得尤为重要。传统银行评价方法多依赖单一财务指标或主观判断，存在评价维度有限、权重设置主观等问题。本研究基于多指标综合评价理论 ，结合熵权法 和灰色关联分析法，开发了一套客观、系统的银行综合评价模型，旨在：

解决多指标综合评价中的权重确定问题
消除不同量纲指标的影响
提供直观的可视化分析结果
提供决策支持

二、主要功能

1. 数据预处理模块

Excel数据自动导入与清洗
指标正向化处理（正向/负向指标转换）
数据标准化（消除量纲影响）

2. 权重计算模块

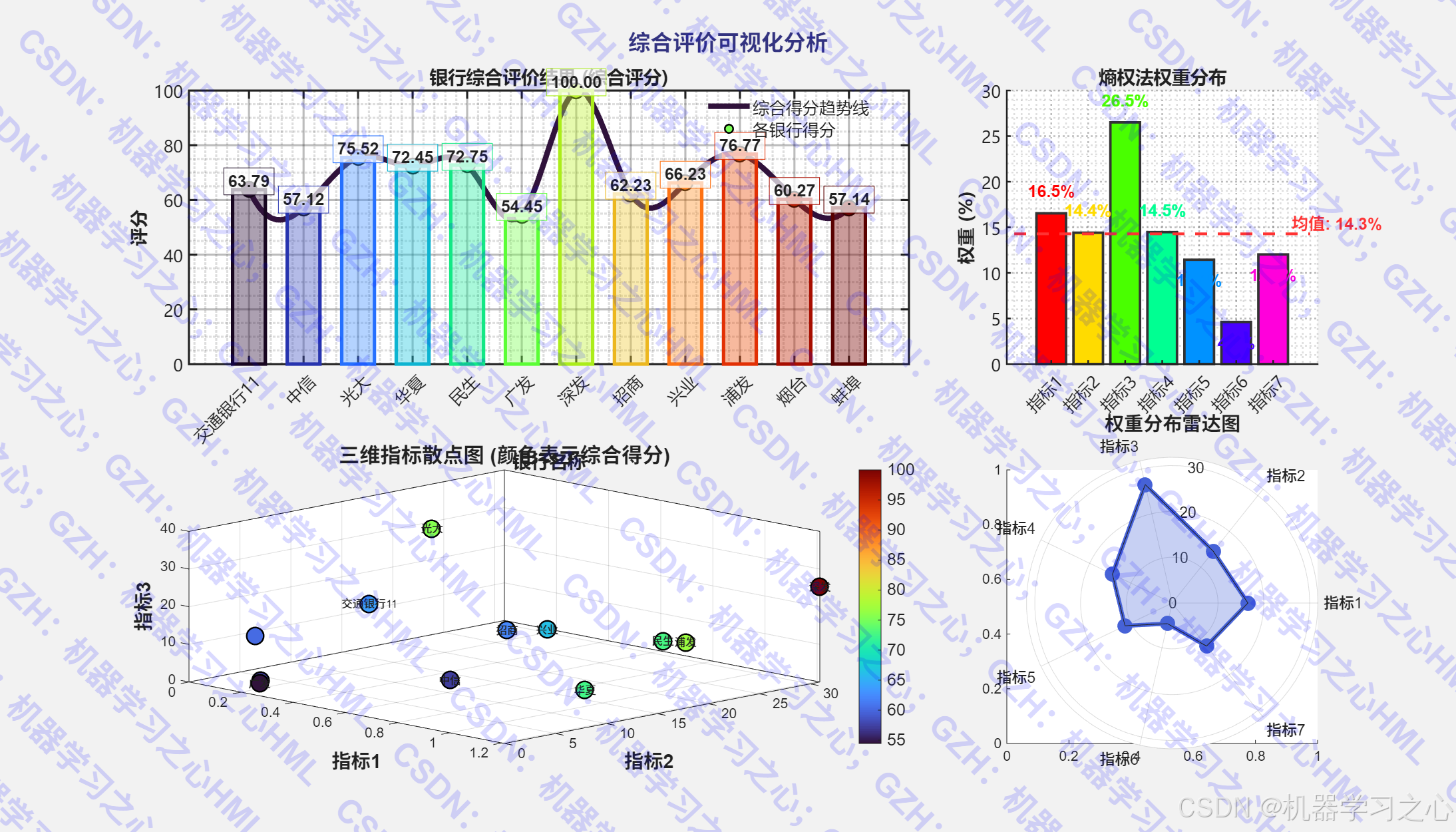
基于熵权法的客观权重计算
权重可视化展示

3. 综合评价模块

灰色关联分析法计算综合得分
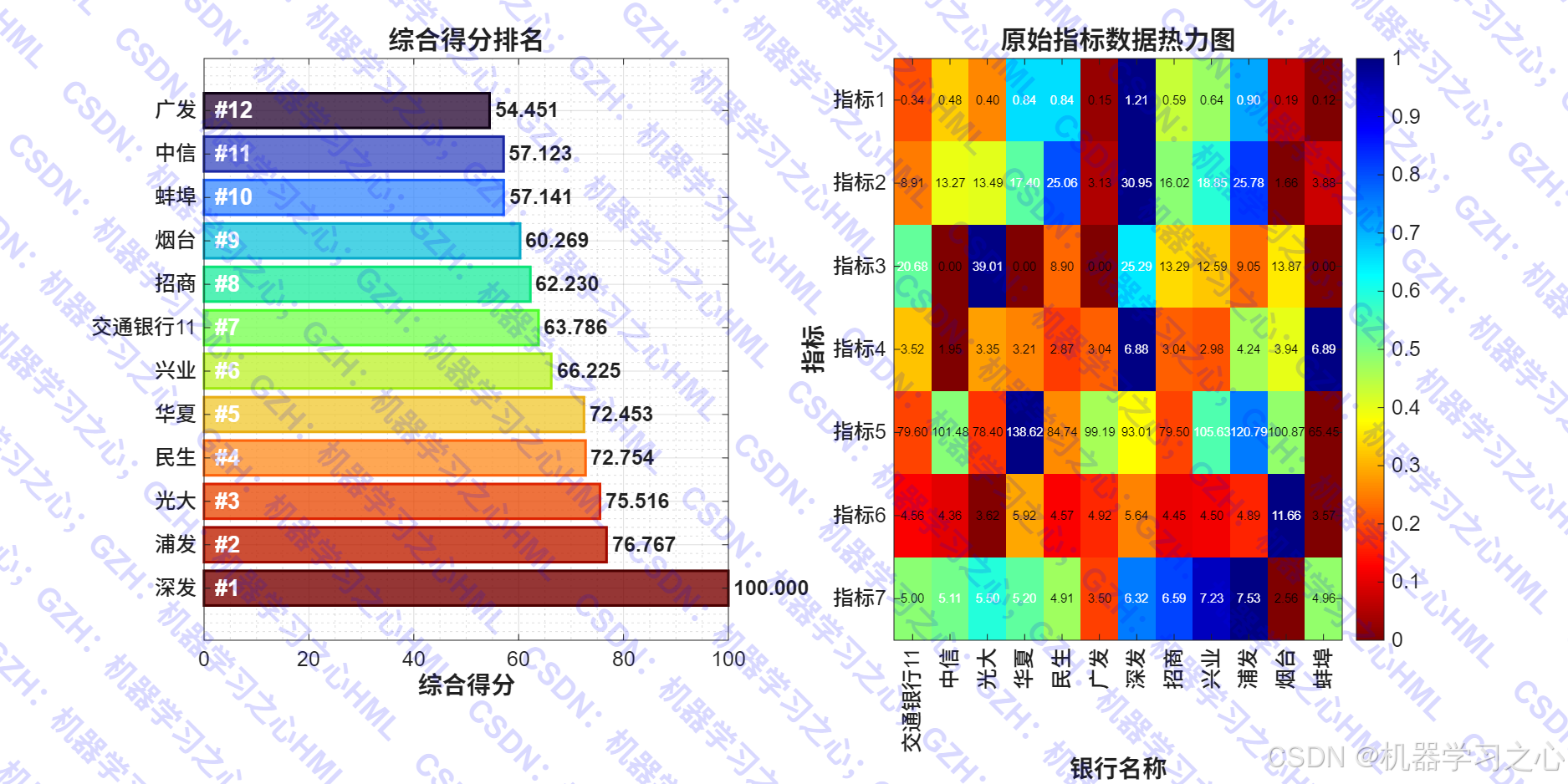
银行排名生成

4. 可视化展示模块

二维曲线图与柱状图组合
三维散点图（多指标关系展示）
雷达图（权重分布）
热力图（原始数据分布）
水平排名图

5. 结果输出模块

命令行结果输出
图形文件保存
数据表格输出

三、算法步骤

Step 1: 数据预处理

读取Excel数据：银行名称 + N个指标
指标正向化处理：
- 正向指标：保持不变
- 负向指标：取倒数或线性变换
数据标准化：
Anormalized=A/sqrt(∑(A2)) A_normalized = A / sqrt(∑(A²)) Anormalized=A/sqrt(∑(A2))

Step 2: 熵权法计算权重

计算第j项指标的熵值：
ej=−k∗Σ(pij∗ln(pij))其中：pij=xij/Σ(xij),k=1/ln(n) e_j = -k * Σ(p_ij * ln(p_ij)) 其中：p_ij = x_ij / Σ(x_ij), k = 1/ln(n) ej=−k∗Σ(pij∗ln(pij))其中：pij=xij/Σ(xij),k=1/ln(n)
计算差异系数：
dj=1−ej d_j = 1 - e_j dj=1−ej
计算权重：
wj=dj/Σ(dj) w_j = d_j / Σ(d_j) wj=dj/Σ(dj)

Step 3: 灰色关联分析

确定参考序列：
X0=max(Anormalized,[],1) X0 = max(A_normalized, [], 1) % 各指标最优值 X0=max(Anormalized,[],1)
计算关联系数：
ξij=(minmin+ρ∗maxmax)/(Δij+ρ∗maxmax)其中：Δij=∣X0j−Xij∣,ρ=0.5（分辨系数） ξ_ij = (min_min + ρ*max_max) / (Δ_ij + ρ*max_max) 其中：Δ_ij = |X0_j - X_ij|, ρ=0.5（分辨系数） ξij=(minmin+ρ∗maxmax)/(Δij+ρ∗maxmax)其中：Δij=∣X0j−Xij∣,ρ=0.5（分辨系数）
计算关联度：
ri=Σ(wj∗ξij) r_i = Σ(w_j * ξ_ij) ri=Σ(wj∗ξij)
得分转换：

Scorei=100∗ri/max(r) Score_i = 100 * r_i / max(r) % 百分制转换 Scorei=100∗ri/max(r)

四、技术路线

复制代码

数据准备 → 预处理 → 权重计算 → 综合评价 → 可视化展示
    ↓          ↓          ↓          ↓          ↓
 Excel导入  正向化处理  熵权法   灰色关联   多种图形
             标准化       权重       分析      输出

具体流程：

输入层：Excel格式指标数据
处理层 ：
- 数据清洗与格式转换
- 指标正向化
- 标准化处理
算法层 ：
- 熵权法计算权重
- 灰色关联分析
输出层 ：
- 数值结果（得分、排名、权重）
- 可视化图形

五、公式原理

1. 熵权法原理

信息熵：ej=−k∑i=1npijln(pij) 信息熵：e_j = -k ∑{i=1}^n p{ij} ln(p_{ij}) 信息熵：ej=−ki=1∑npijln(pij)
差异系数：dj=1−ej 差异系数：d_j = 1 - e_j 差异系数：dj=1−ej
权重：wj=dj/∑j=1mdj 权重：w_j = d_j / ∑_{j=1}^m d_j 权重：wj=dj/j=1∑mdj

特点：指标差异越大 → 熵值越小 → 权重越大

2. 灰色关联分析原理

关联系数：ξi(k)=[minmin∣x0(k)−xi(k)∣+ρmaxmax∣x0(k)−xi(k)∣]/[∣x0(k)−xi(k)∣+ρmaxmax∣x0(k)−xi(k)∣] 关联系数：ξ_i(k) = [min min |x_0(k)-x_i(k)| + ρ max max |x_0(k)-x_i(k)|] / [|x_0(k)-x_i(k)| + ρ max max |x_0(k)-x_i(k)|] 关联系数：ξi(k)=[minmin∣x0(k)−xi(k)∣+ρmaxmax∣x0(k)−xi(k)∣]/[∣x0(k)−xi(k)∣+ρmaxmax∣x0(k)−xi(k)∣]
关联度：ri=1/n∑k=1nξi(k) 关联度：r_i = 1/n ∑_{k=1}^n ξ_i(k) 关联度：ri=1/nk=1∑nξi(k)

加权关联度：ri′=∑k=1nwk∗ξi(k) 加权关联度：r_i' = ∑_{k=1}^n w_k * ξ_i(k) 加权关联度：ri′=k=1∑nwk∗ξi(k)

3. 数据标准化公式

向量归一化：xi′j=xij/√(∑i=1nxij2) 向量归一化：x'ij = x_ij / √(∑{i=1}^n x_ij²) 向量归一化：xi′j=xij/√(i=1∑nxij2)

六、参数设定

指标类型标签

1: 正向指标（越大越好）

2: 正向指标2（可选分类）

3: 负向指标（越小越好）

灰色关联分辨系数

ρ = 0.5;

2. 权重计算参数

k=1/log(n);epsilon=1e−10; k = 1/log(n); % 熵值计算常数，n为样本数 epsilon = 1e-10; % 防止log(0)的小量 k=1/log(n);epsilon=1e−10;

七、运行环境

软件要求

MATLAB版本：R2020b 或更高版本

八、应用场景

1. 银行内部管理

绩效评估：各分支行/业务部门综合排名
风险管理：多维度风险评估与预警
资源配置：基于评价结果的资源优化分配

2. 投资分析

股票筛选：银行股投资价值评估
信用评级：银行信用风险量化分析
行业比较：不同银行间竞争力对比

3. 监管评估

系统性风险：识别高风险银行机构
合规检查：多指标合规性综合评价
政策效果：评估监管政策实施效果

4. 学术研究

方法比较：不同综合评价方法对比
指标体系：银行评价指标体系优化
实证分析：银行业发展状况研究

5. 其他金融机构

保险公司：分支机构绩效评价
证券公司：营业部综合排名
基金公司：投资对象筛选