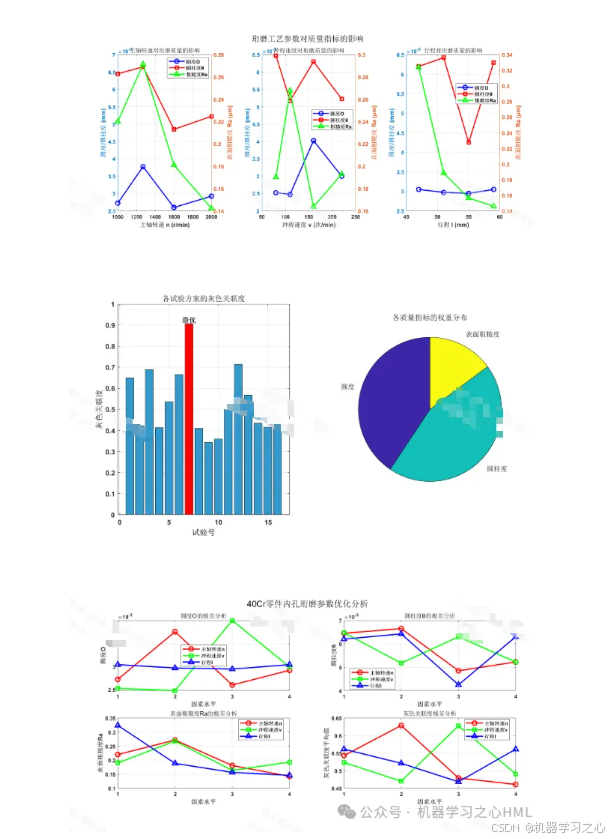
MATLAB基于极差法和灰色关联分析的40Cr零件内孔珩磨参数优化

目标：在多个性能指标（通常是表面粗糙度Ra越小越好，材料去除率MRR越大越好）之间取得平衡，找到一组最优的珩磨工艺参数组合。
核心方法 ：采用正交试验设计 安排试验，使用极差法 分析各参数对单一指标的主次影响，再运用灰色关联分析将多指标转化为单一的综合评价指标（灰色关联度），从而找到全局最优参数组合。

优化步骤详解

步骤一：明确优化目标与评价指标

质量指标（望小特性）：表面粗糙度（Ra）。值越小，表面质量越高。
效率指标（望大特性） ：材料去除率（MRR）。值越大，加工效率越高。
这两个指标往往相互矛盾，需要多目标优化。

步骤二：选定关键珩磨参数与水平

根据工艺知识和前期研究，选择对Ra和MRR影响显著的3个关键参数，每个参数设置3个水平（以常见范围为例）：

因素代码	珩磨参数	水平1	水平2	水平3
A	砂条压力 (MPa)	0.4	0.6	0.8
B	往复速度 (m/min)	10	15	20
C	圆周速度 (m/min)	30	40	50

步骤三：设计正交试验并进行试验

选择 L9(3⁴) 正交表（4因素3水平，共9组试验）。将上述3个因素填入表头，进行9次珩磨试验，并测量每次试验后的Ra和MRR。

试验号	A:压力	B:往复速度	C:圆周速度	Ra (μm)	MRR (mm³/min)
1	0.4	10	30	Ra1	MRR1
2	0.4	15	40	Ra2	MRR2
3	0.4	20	50	Ra3	MRR3
4	0.6	10	40	Ra4	MRR4
5	0.6	15	50	Ra5	MRR5
6	0.6	20	30	Ra6	MRR6
7	0.8	10	50	Ra7	MRR7
8	0.8	15	30	Ra8	MRR8
9	0.8	20	40	Ra9	MRR9

步骤四：灰色关联分析（GRA）

目的：将Ra和MRR两个量纲和趋向不同的指标，归一化为一个可比较的综合指标------灰色关联度（GRG）。

数据预处理（归一化）：
- 对于Ra（望小） ：x_i*(k) = (max Ra - Ra_i) / (max Ra - min Ra)
- 对于MRR（望大） ：x_i*(k) = (MRR_i - min MRR) / (max MRR - min MRR)
  处理后，所有序列值均在 $0, 1$ 之间，且值越大越好。
计算关联系数 ：

将预处理后的每个试验序列视为一个比较序列，构造一个参考序列X0 ，其所有值均为1（理想最优状态）。

计算比较序列Xi与参考序列X0在各指标（k点）上的关联系数 ξ_i(k)：
ξ_i(k) = (Δ_min + ρ * Δ_max) / (Δ_i(k) + ρ * Δ_max)

其中：
- Δ_i(k) = |x0(k) - x_i*(k)|，即差值。
- Δ_min 和 Δ_max 分别是所有差值中的最小值和最大值。
- ρ 是分辨系数，通常取0.5。
计算灰色关联度（GRG） ：

将每个试验号（i）在两个指标（k=Ra, MRR）上的关联系数进行等权平均，得到该组参数的综合评分------灰色关联度γ_i。
γ_i = (1/2) * [ξ_i(Ra) + ξ_i(MRR)]
γ_i 越大，说明该组参数的综合性能越接近理想最优状态。

步骤五：基于灰色关联度的极差分析

现在，我们将每个试验号计算出的灰色关联度γ作为单一响应值，填入正交表，进行传统的极差分析。

试验号	A	B	C	灰色关联度 (γ)
1	1	1	1	γ1
2	1	2	2	γ2
...	...	...	...	...
9	3	3	2	γ9

计算各因素水平下的均值：
- 对于因素A在水平1（0.4MPa）下的均值 K_A1 = (γ1 + γ2 + γ3) / 3
- 同理计算 K_A2, K_A3；K_B1, K_B2, K_B3；K_C1, K_C2, K_C3。
计算极差R：
- 对于因素A，极差 R_A = max(K_A1, K_A2, K_A3) - min(K_A1, K_A2, K_A3)
- 同理计算 R_B, R_C。
分析结果：
- 主次顺序 ：比较R_A, R_B, R_C。极差越大，表示该因素对综合性能（灰色关联度）的影响越大。主次顺序为：R_最大因素 > R_次大因素 > R_最小因素。
- 最优水平组合 ：观察每个因素下K_A1、K_A2、K_A3中数值最大的水平，即为该因素的最优水平。将所有因素的最优水平组合起来，即得到理论上的多目标最优参数组合。

步骤六：验证试验

根据极差分析得出的最优参数组合（例如：A2B3C1），在相同条件下进行1-2次验证试验。测量实际的Ra和MRR，并计算其灰色关联度。将此关联度与正交试验中最高的一次（γ_i）进行比较，若验证试验的关联度更高或相当，则证明优化有效。

结论与输出

通过上述流程，你可以得到：

推荐的最优参数组合 ：例如，A2B3C1（砂条压力0.6MPa，往复速度20 m/min，圆周速度30 m/min）。
定量的优化效果：验证试验的综合性能（灰色关联度）较初始经验参数有显著提升，实现了在保证表面质量（Ra）的同时，尽可能提高加工效率（MRR）的目标。

优势：该方法将复杂的多目标问题结构化、数据化，通过较少的试验次数（9次），科学地揭示了参数的影响规律并找到最优解，特别适用于生产过程优化。对于40Cr这种材料，优化的参数能有效平衡其硬度与韧性带来的加工挑战，提升珩磨工艺的稳健性。