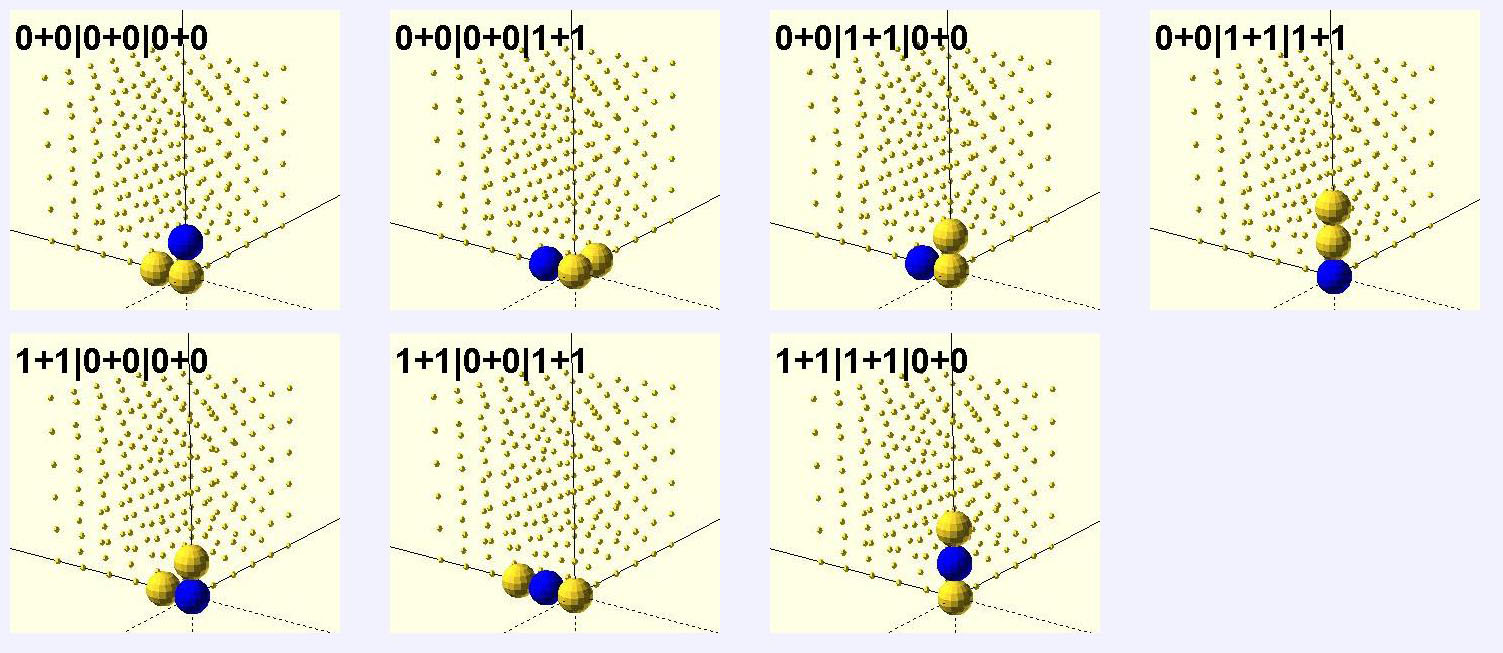
在模长,方位角,极角自由变化的球坐标系内3点结构有7个
|---|---|---|---|---|---|---|---|---|---|
| 模长 || | | 方位角 || | | 极角 ||
| 1 | 1 | | | 1 | 1 | | | 0 | 0 |
| | | | | | | | | | |
| 1 | 1 | | | 0 | 0 | | | 1 | 1 |
| 1 | 1 | | | 0 | 0 | | | 0 | 0 |
| | | | | | | | | | |
| 0 | 0 | | | 1 | 1 | | | 1 | 1 |
| 0 | 0 | | | 1 | 1 | | | 0 | 0 |
| | | | | | | | | | |
| 0 | 0 | | | 0 | 0 | | | 1 | 1 |
| 0 | 0 | | | 0 | 0 | | | 0 | 0 |
按照排列组合共有8个,还有1+1|1+1|1+1,但如果模长,方位角和极角都相同这两个点是重合的,因此排除,剩余的7个都存在。
这7个结构之间存在加法关系
(0+0|0+0|0+0)+(0|0|1)=(0+0|0+0|1+1)
(0+0|0+0|0+0)+(0|1|0)=(0+0|1+1|0+0)
**
(0+0|0+0|1+1)+(0|1|0)=(0+0|1+1|1+1)
**
(0+0|1+1|0+0)+(0|0|1)=(0+0|1+1|1+1)
**
(0+0|0+0|0+0)+(1|0|0)=(1+1|0+0|0+0)
**
(1+1|0+0|0+0)+(0|0|1)=(1+1|0+0|1+1)
(1+1|0+0|0+0)+(0|1|0)=(1+1|1+1|0+0)
所以这7个结构通过有限次的加减法都可以相互转换。如果把1+1用1表示,得到
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 模长 || | | 方位角 || | | 极角 || | | | | |
| 1 | 1 | | | 1 | 1 | | | 0 | 0 | | | 1 | 1 | 0 |
| | | | | | | | | | | | | | | |
| 1 | 1 | | | 0 | 0 | | | 1 | 1 | | | 1 | 0 | 1 |
| 1 | 1 | | | 0 | 0 | | | 0 | 0 | | | 1 | 0 | 0 |
| | | | | | | | | | | | | | | |
| 0 | 0 | | | 1 | 1 | | | 1 | 1 | | | 0 | 1 | 1 |
| 0 | 0 | | | 1 | 1 | | | 0 | 0 | | | 0 | 1 | 0 |
| | | | | | | | | | | | | | | |
| 0 | 0 | | | 0 | 0 | | | 1 | 1 | | | 0 | 0 | 1 |
| 0 | 0 | | | 0 | 0 | | | 0 | 0 | | | 0 | 0 | 0 |
所有这7种离散运动状态都可以用3个整数表示
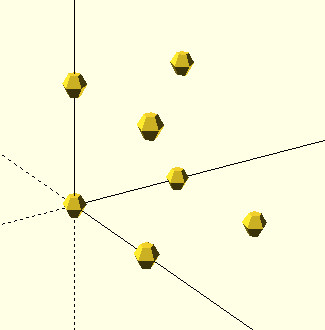
|-----------|----|
| (1|0|0) | z轴 |
| (0|1|0) | x轴 |
| (0|0|1) | y轴 |
现已知
如果存在1,0,0的运动状态,就一定存在2,0,0;3,0,0;4,0,0的运动状态,假设这种可以表示为n,0,0的运动状态的n的意义为空间的分辨率,如果一个点由1,0,0的状态变化到2,0,0的状态空间的分辨率变大,就像看视频由100*100变成200*200,点与点之间的距离变小了,图像变得更清晰,运动的细节更丰富。显然n越大,分辨率越大,点与点之间的距离d越小,如果d趋近于0,自然就完成了由离散到连续的过渡。
分辨率越大,点与点之间的距离越小,用来观察的光波长越小,频率越大,能量越大;因此由1,0,0到n,0,0的过程是吸收能量的,让n只能是整数,能量一定是量子化的。
因此能不能认为量子力学主量子数的物理意义就是空间分辨率?