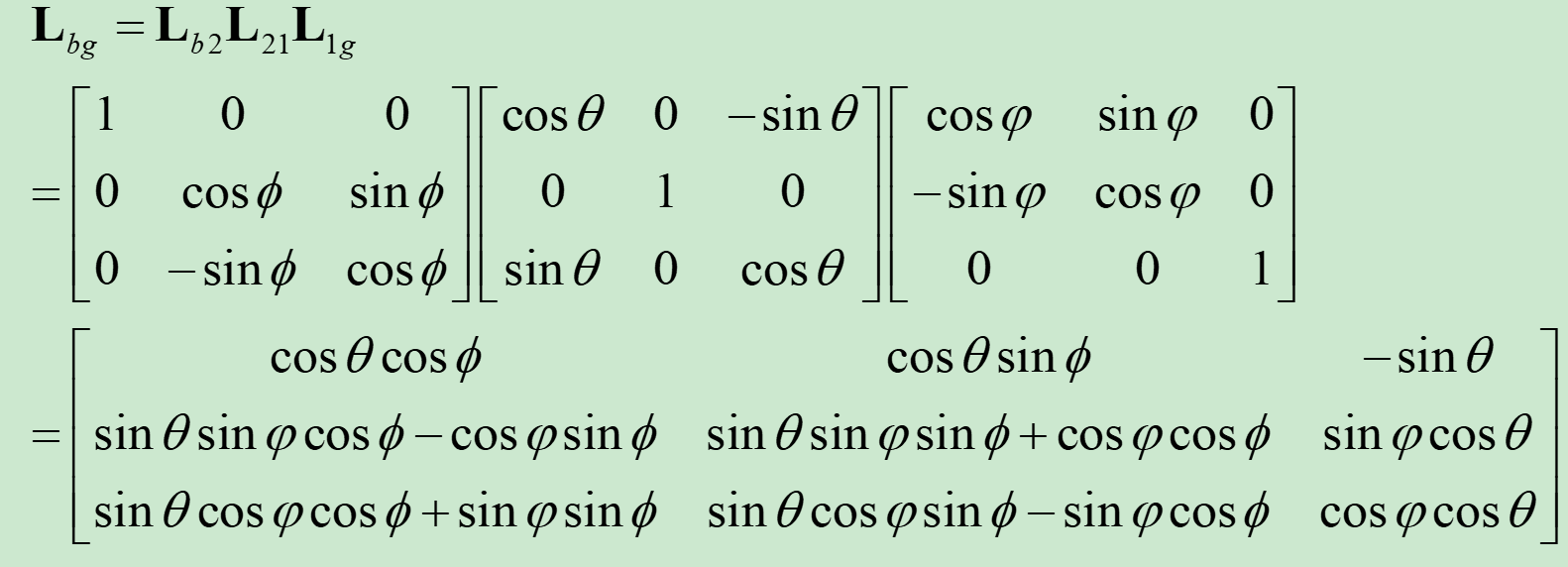一、二维坐标系旋转矩阵
假设平面坐标系Oxqyq逆时针旋转α角后得到坐标系Oxpyp,如下图所示:从Q点分别向ER和OP作垂线,垂足分别为F、P。
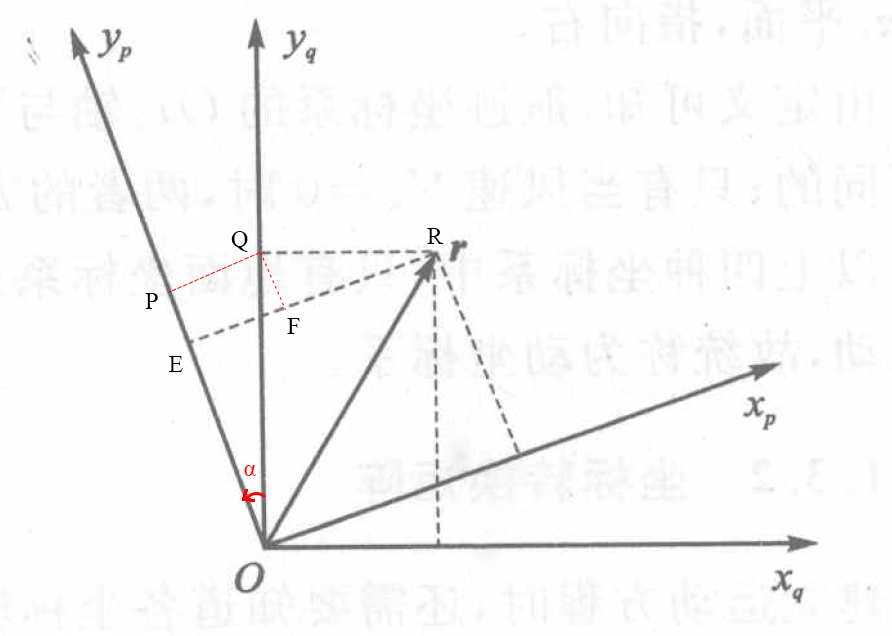
图1 平面坐标系旋转关系
从图中可以得到:
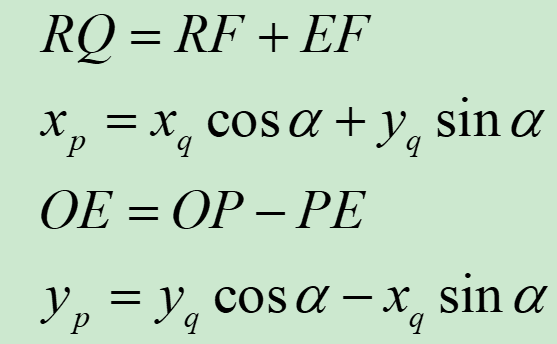
写成矩阵形式,矢量r在Oxqyq坐标系中的坐标(xq,yq)与在Oxpyp坐标系中的坐标存在以下几何关系:
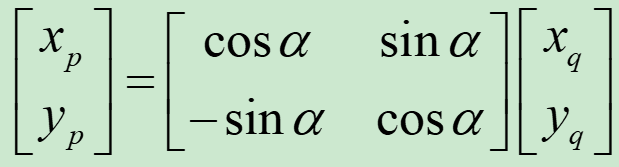
记:
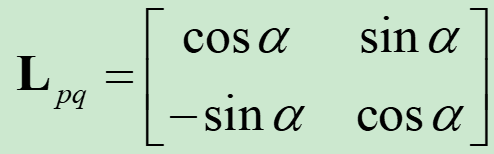
Lqp即为Oxqyq坐标系到Oxpyp坐标系转换矩阵,也即大名鼎鼎的Givens旋转矩阵。Givens旋转矩阵有以下重要性质:
1、Givens矩阵为正交矩阵,有以下关系:
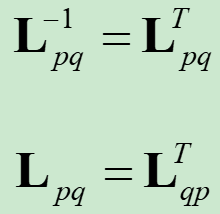
2、传递性:
设有三个坐标系Sp ,Sq , S r , 矢量r在这三个坐标系的分量阵可用相应的转换矩阵联系起来,并且Lpr仍为正交矩阵,即:
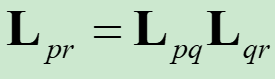
二、三维坐标系转换矩阵
基于以上平面坐标系的旋转矩阵和旋转矩阵的传递性质,可以利用三维坐标系的单轴旋转矩阵推导出三维坐标系转换矩阵。
2.1 绕z轴旋转的旋转矩阵
假设绕z轴逆时针旋转φ角:得到过渡坐标系x1y1zg。
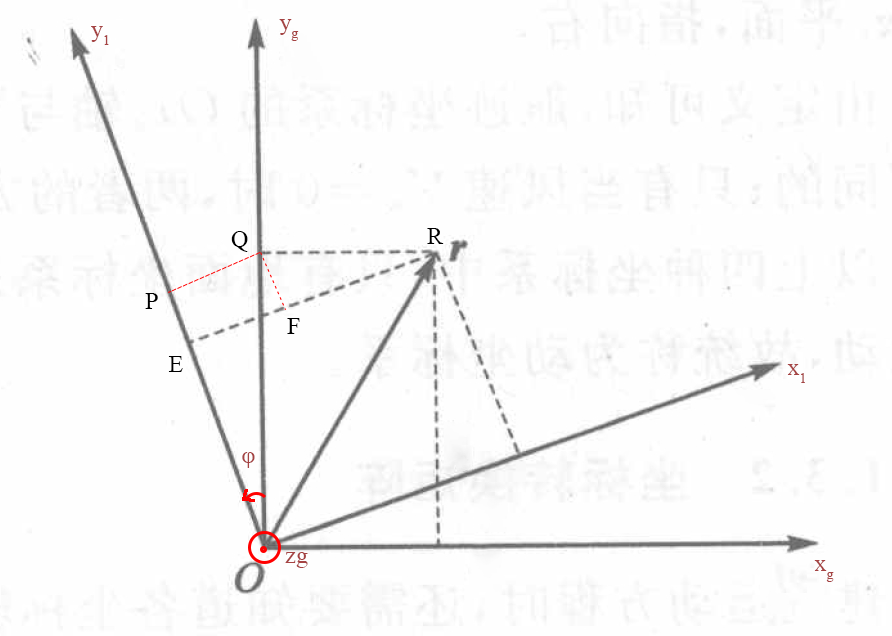
图4 绕x轴旋转示意
L1g转换矩阵如下:
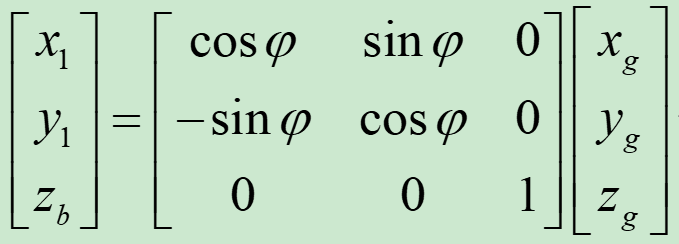
2.2 绕y轴旋转的旋转矩阵
假设绕y轴逆时针旋转θ角:得到过渡坐标系x2y1z2。
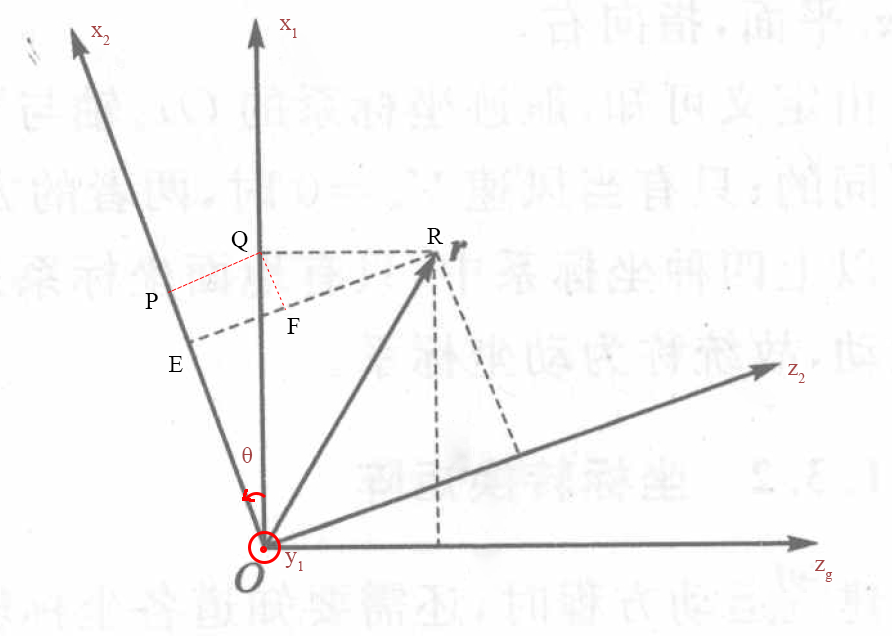
图3 绕y轴旋转示意
L21转换矩阵如下:
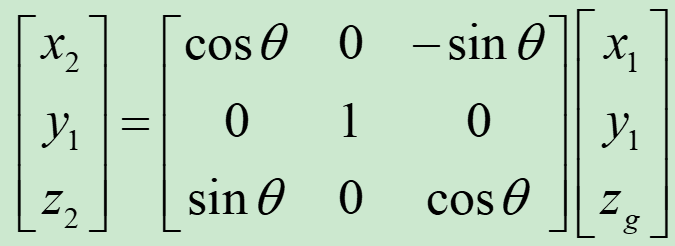
2.3 绕x轴旋转的旋转矩阵
假设绕x轴逆时针旋转ψ角:
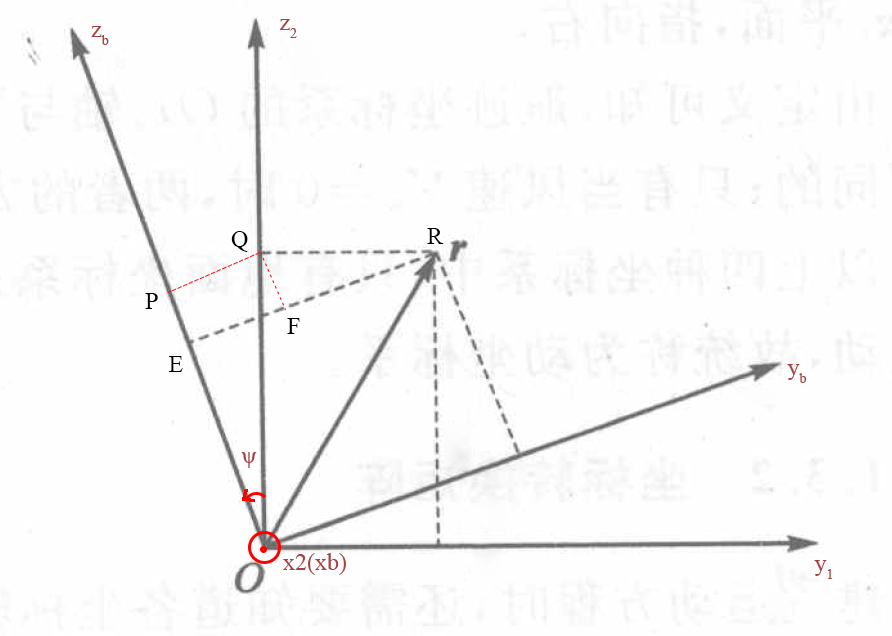
图2 绕x轴旋转示意
Lb2转换矩阵如下:
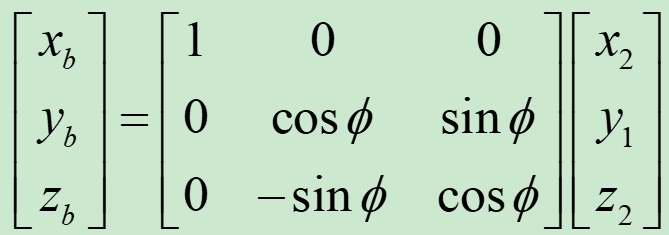
应用传递律可得三维坐标系旋转矩阵: