监督学习
线性回归 (Linear Regression)
线性回归(Linear Regression)是机器学习中最基础且广泛应用的算法之一。
线性回归 (Linear Regression) 是一种用于预测连续值的最基本的机器学习算法,它假设目标变量 y 和特征变量 x 之间存在线性关系,并试图找到一条最佳拟合直线来描述这种关系。
y = w * x + b其中:
-
y是预测值 -
x是特征变量 -
w是权重 (斜率) -
b是偏置 (截距)
线性回归的目标是找到最佳的 w 和 b,使得预测值 y 与真实值之间的误差最小。
Housing price prediction
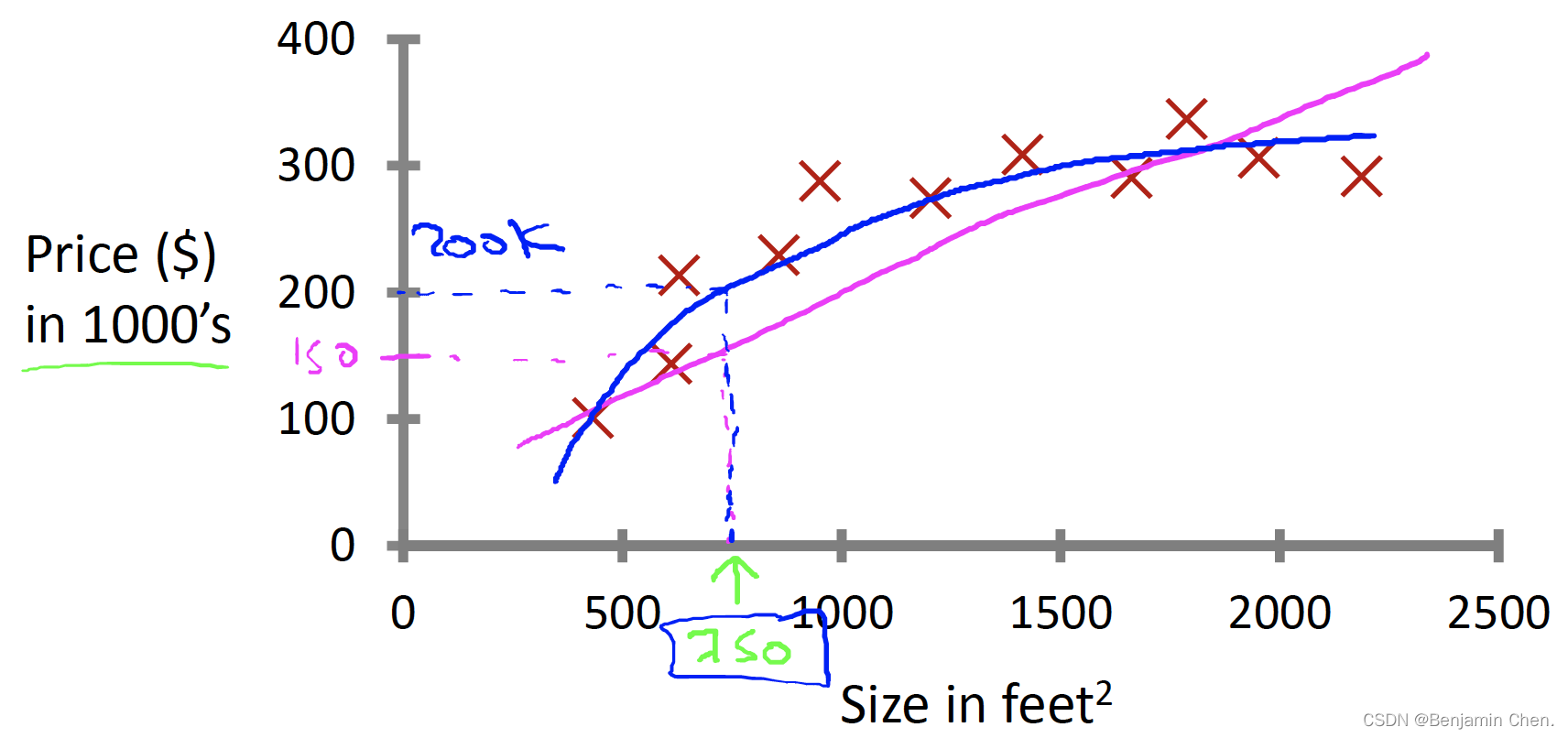
已知一个数据集,已知房子的平方英尺数,预测房子的价格。可以通过一条直线拟合数据,或者通过二次函数拟合数据。如何选择和如何决定用什么拟合数据会有更好的结果。
Supervised Learning"right answers" given →数据集包含正确答案,算法基于正确答案预测更多的正确答案
Regression: Predict continuous valued output (price) →回归问题:预测连续值输出
Breast cancer (malignant, benign)
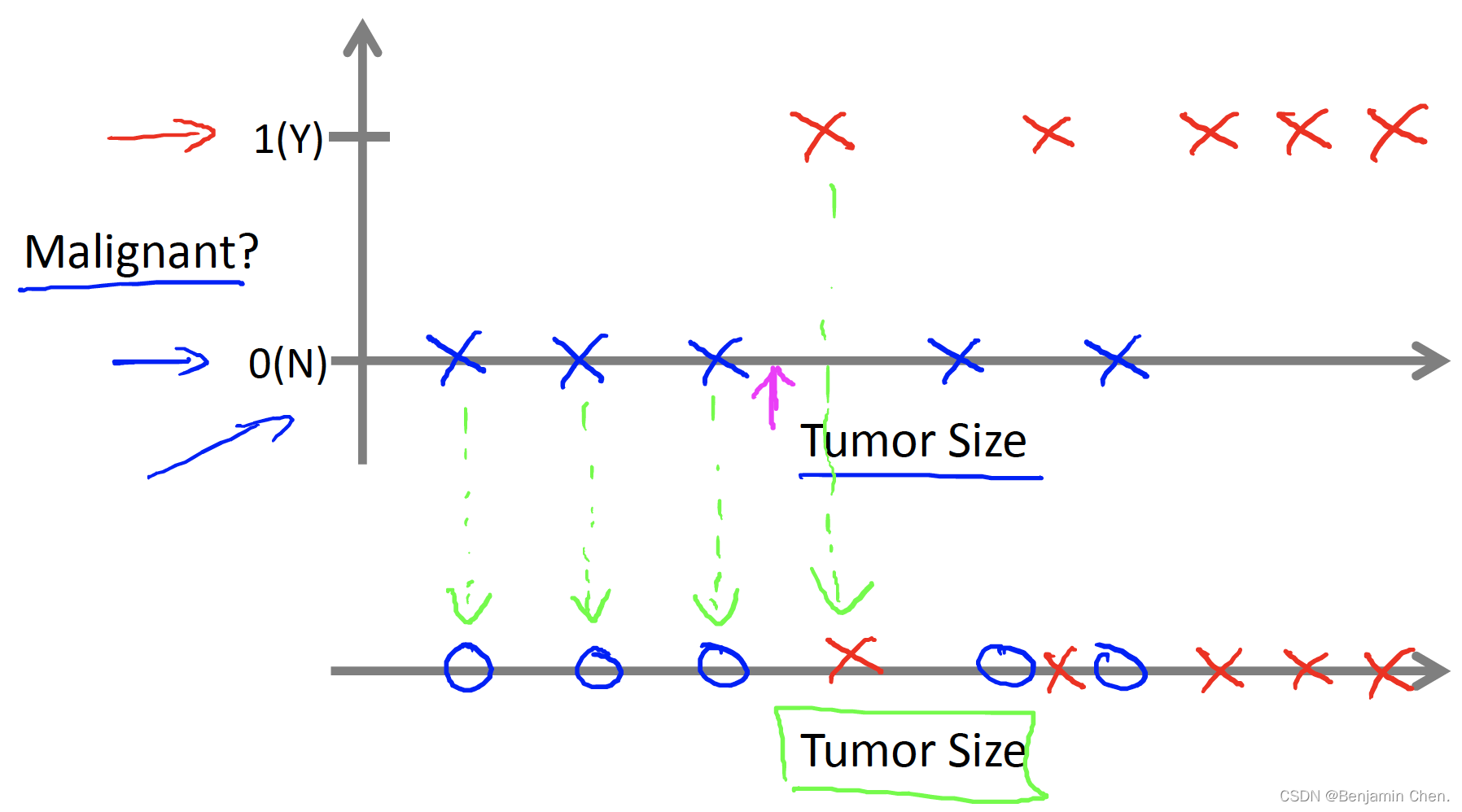
已知一个数据集,已知肿瘤的大小,预测肿瘤是良性还是恶性的概率。
Classification: Discrete valued output (0 or 1) →分类问题:预测一个离散值输出
机器学习会有很多feature特征
Training set of housing prices
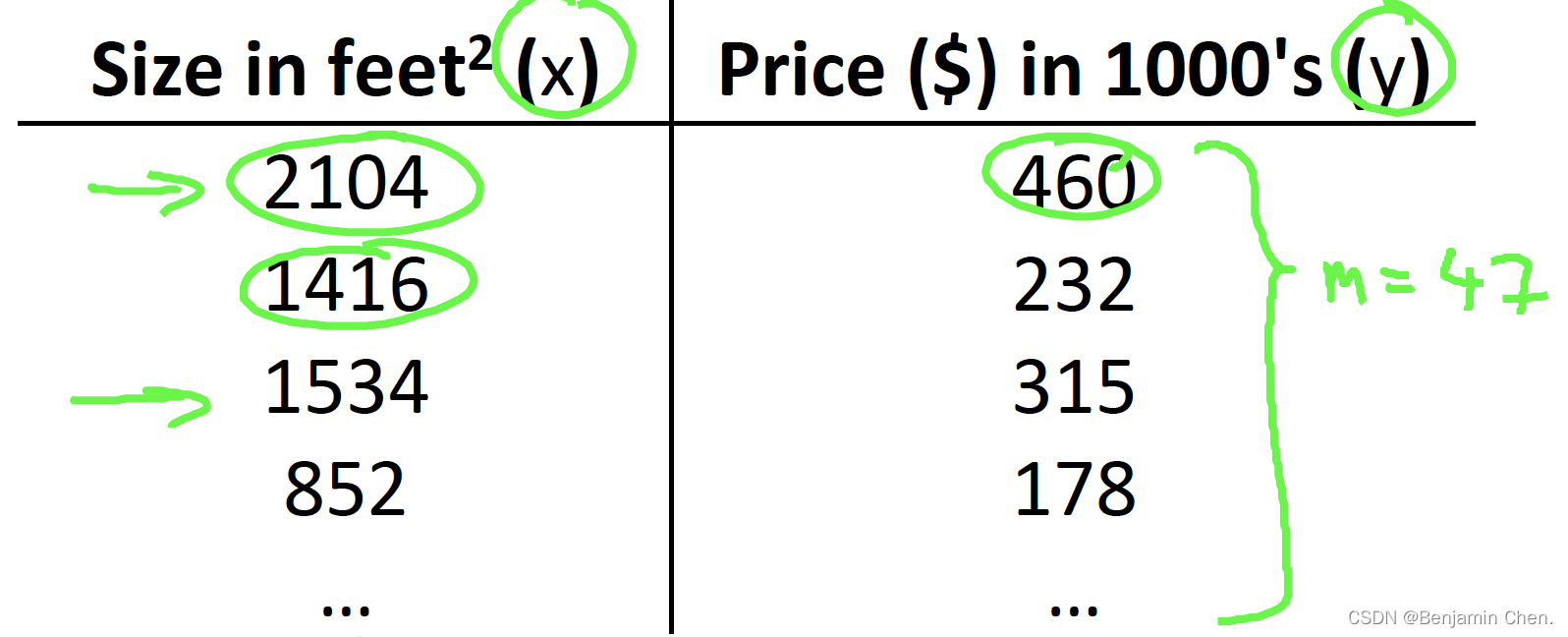
Nocation
m = Number of training examples →训练样本的数量
x's = "input" variable / features →输入变量 / 特征
y's = "output" variable / "target" variable →输出变量 / 目标变量
(x, y) = single training example →一个训练样本
(x(i), y(i)) = ith training example →第i个训练样本
Supervised learning algorithm work
training set → learning algorithm→hypothesis假设函数
h是一个映射x到y的函数
How do we represent h ?
hθ(x)=θ0+θ1x
Linear regression with one variable. = Univariate linear regression →单变量线性回归
θi's: Parameters →模型参数
Cost function
How to choose θi's ?
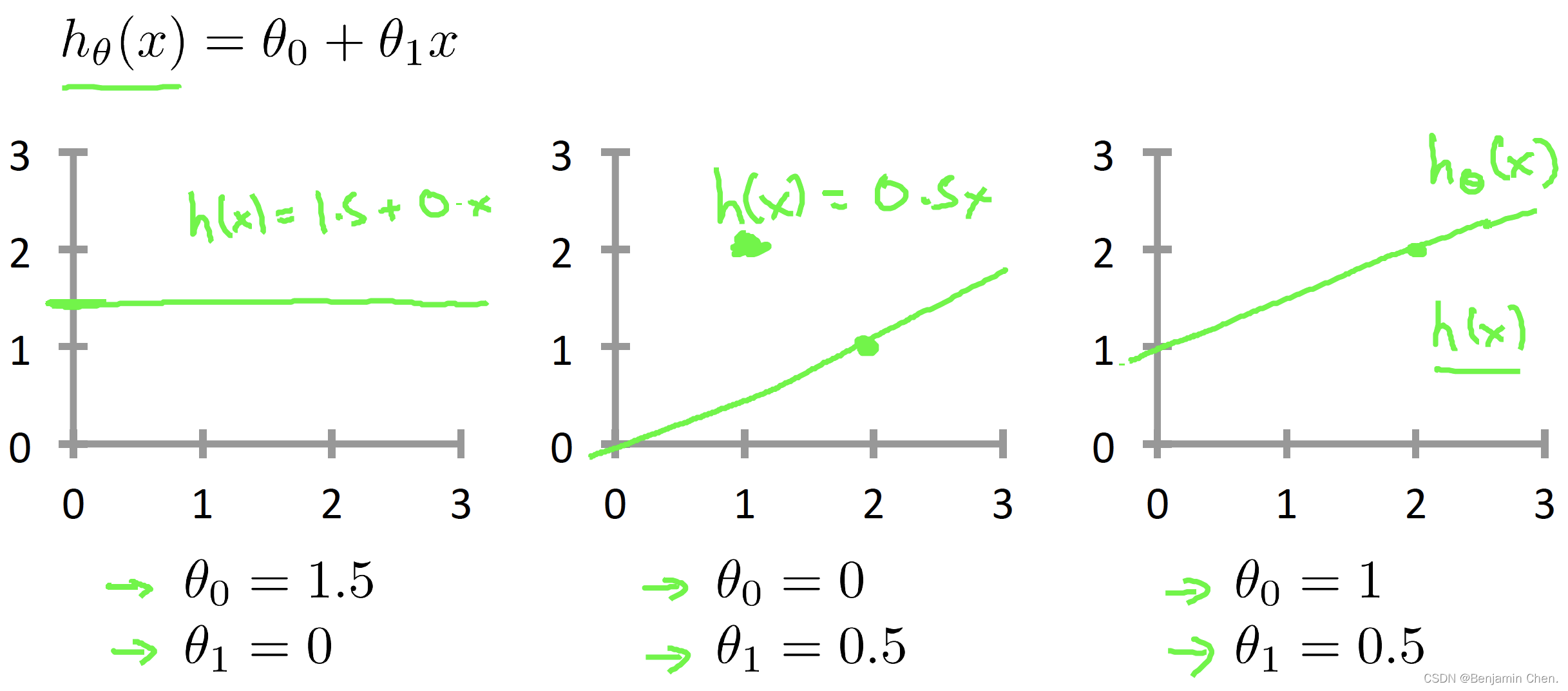
1.选择能使h(x)也就是输入x时预测的值最接近该样本对应的y值的参数θ_0, θ_1
hθ(x) =θ0+θ1x
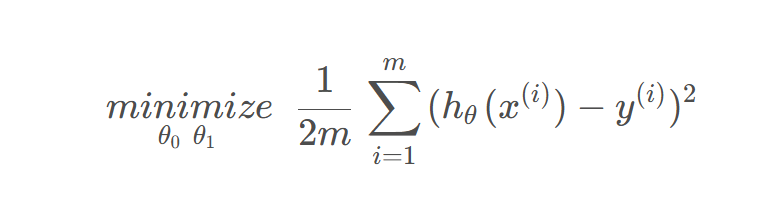
- 找到参数θ0, θ1使得所有训练样本的h(x)预测值和y实际值之间的差的平方和最小化
- m为训练样本的个数
- 1/2m为了减少平均误差(只是为了使数学更加直白一点)
2.cost function代价函数J(θ_0, θ_1)也叫做squared error function平方误差函数
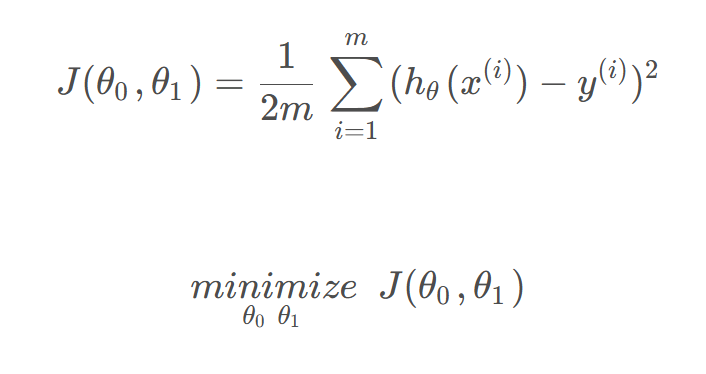
Formulation
Hypotheis:
hθ(x) =θ0+θ1x
Parameters:
θ0, θ1
Cost function:
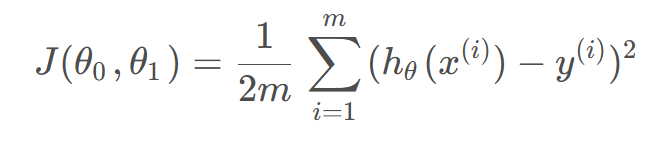
Goal:
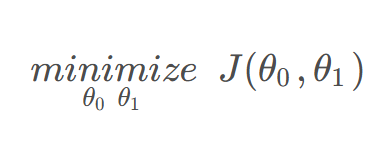
Simplified cost function
hθ(x)= θ1x(θ0= 0)
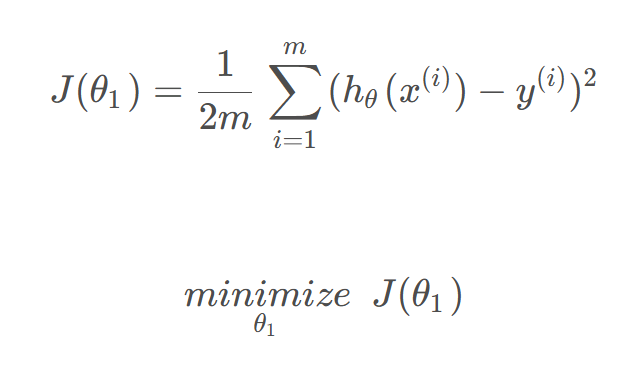
3.如果θ_0=0相当于选择了经过原点的假设函数(过点(0,0)的函数)
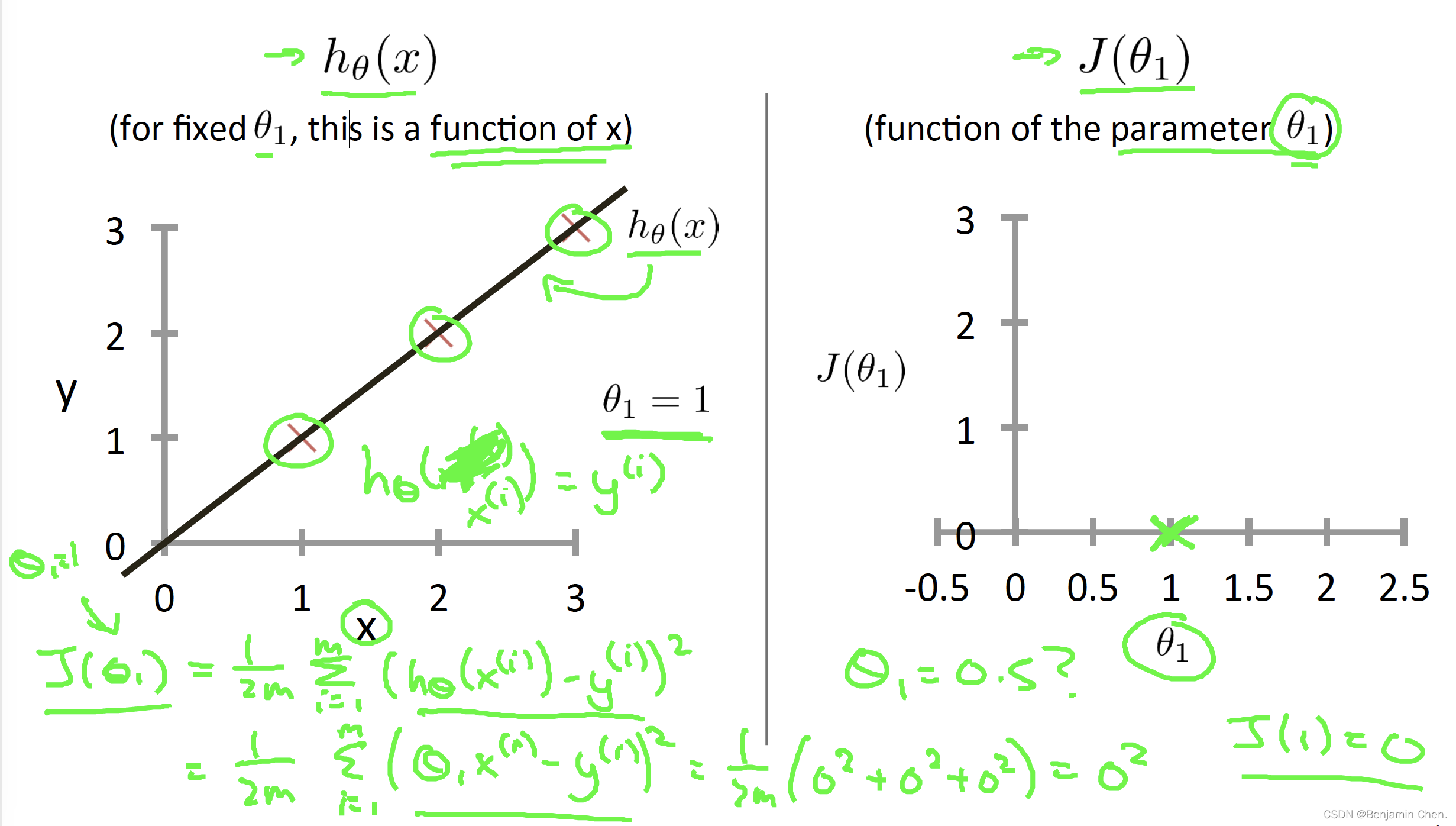
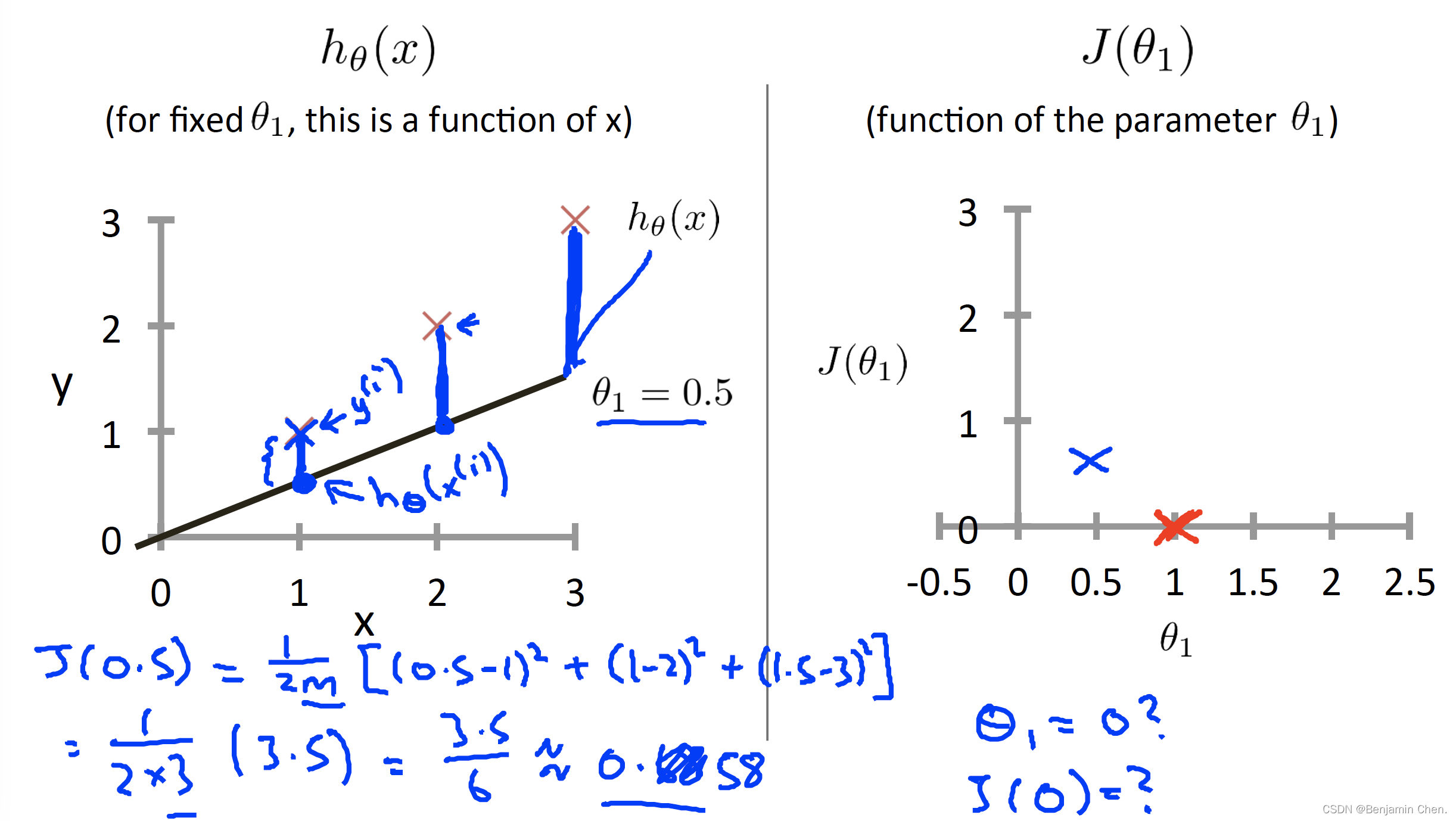
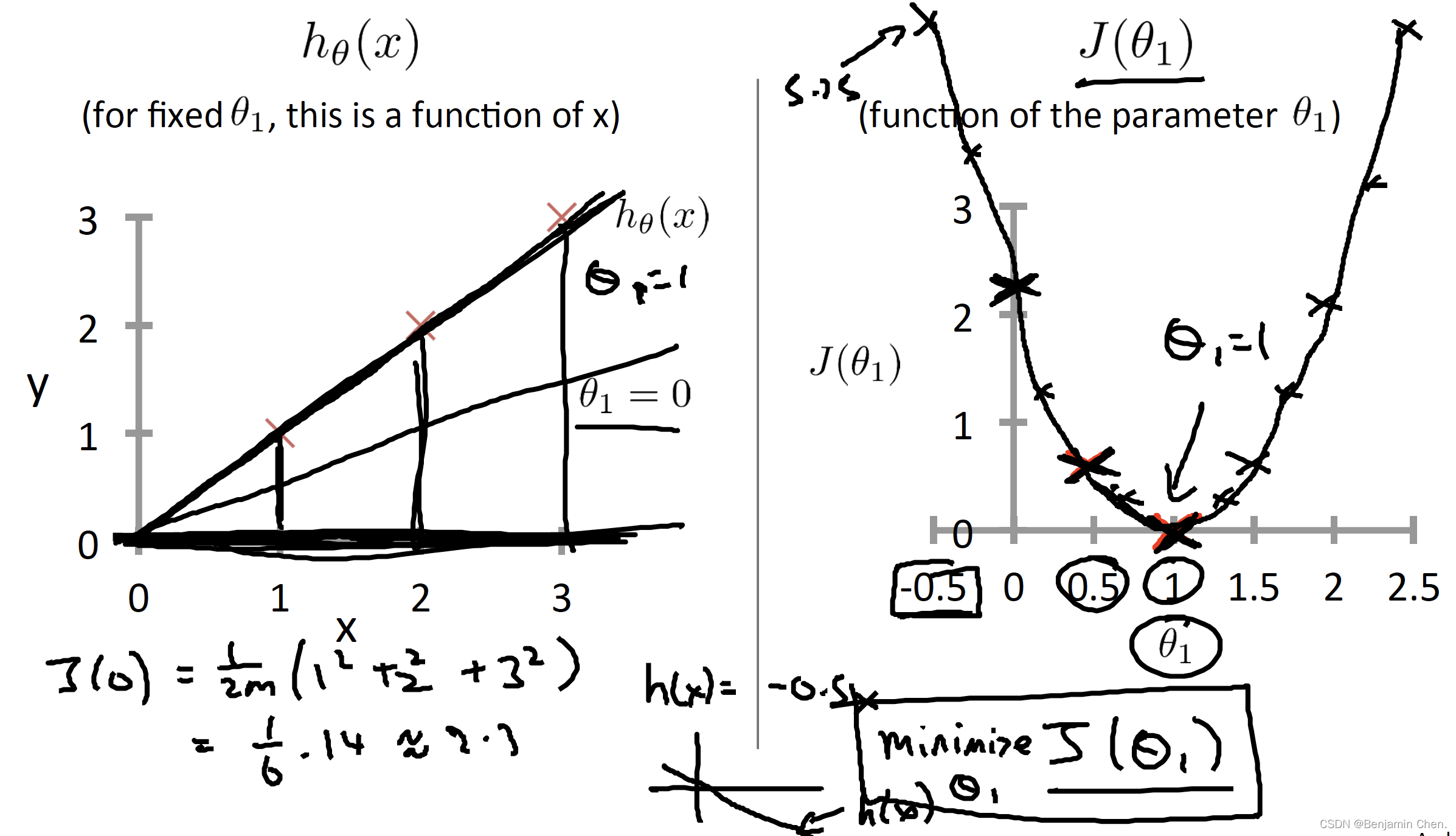
4.分别计算θ_1对应的J(θ_1)可以绘制出J(θ_1)的曲线
5.学习算法的优化目标是通过选择θ_1的值获得最小的J(θ_1)
Two parameters cost function
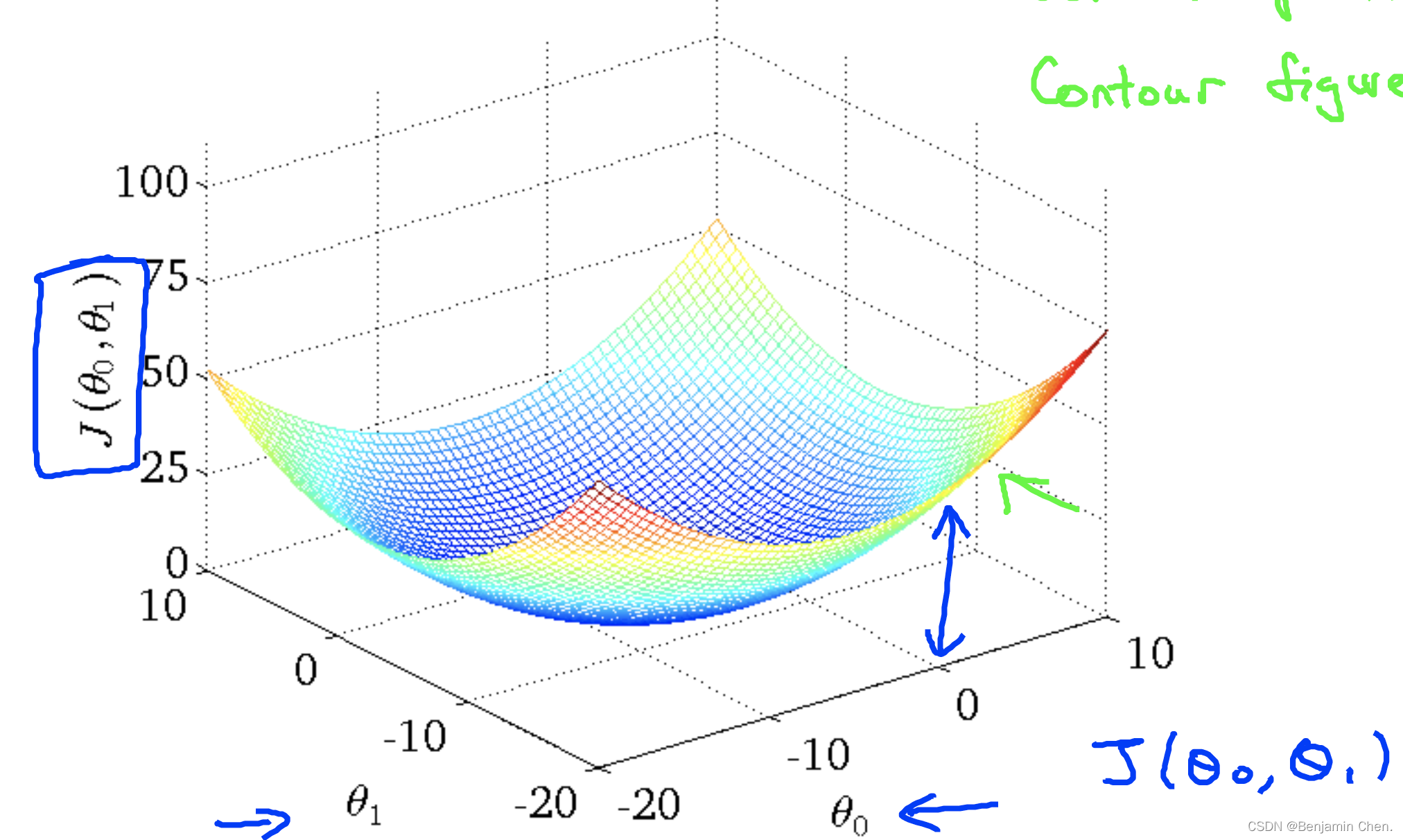
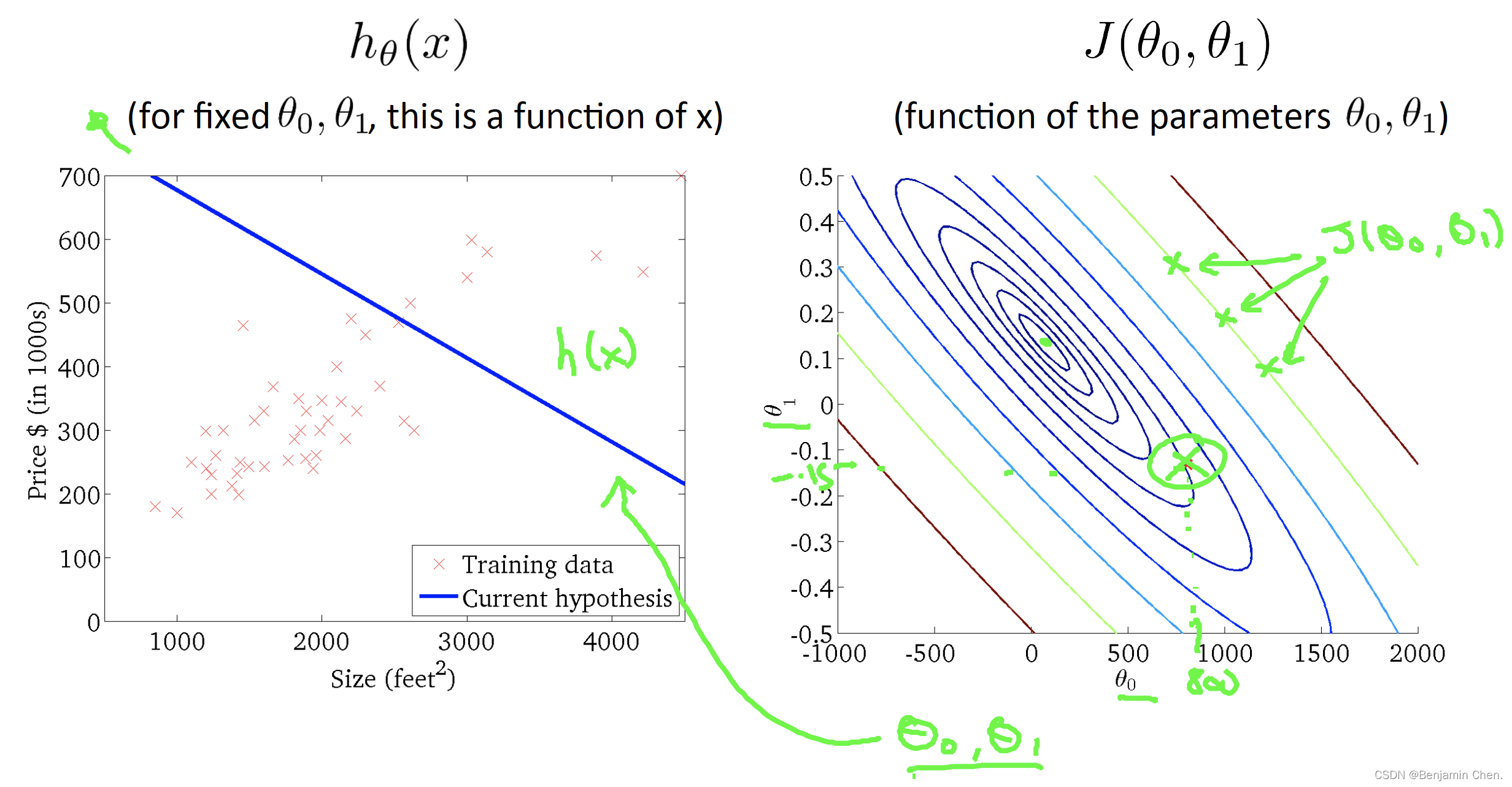
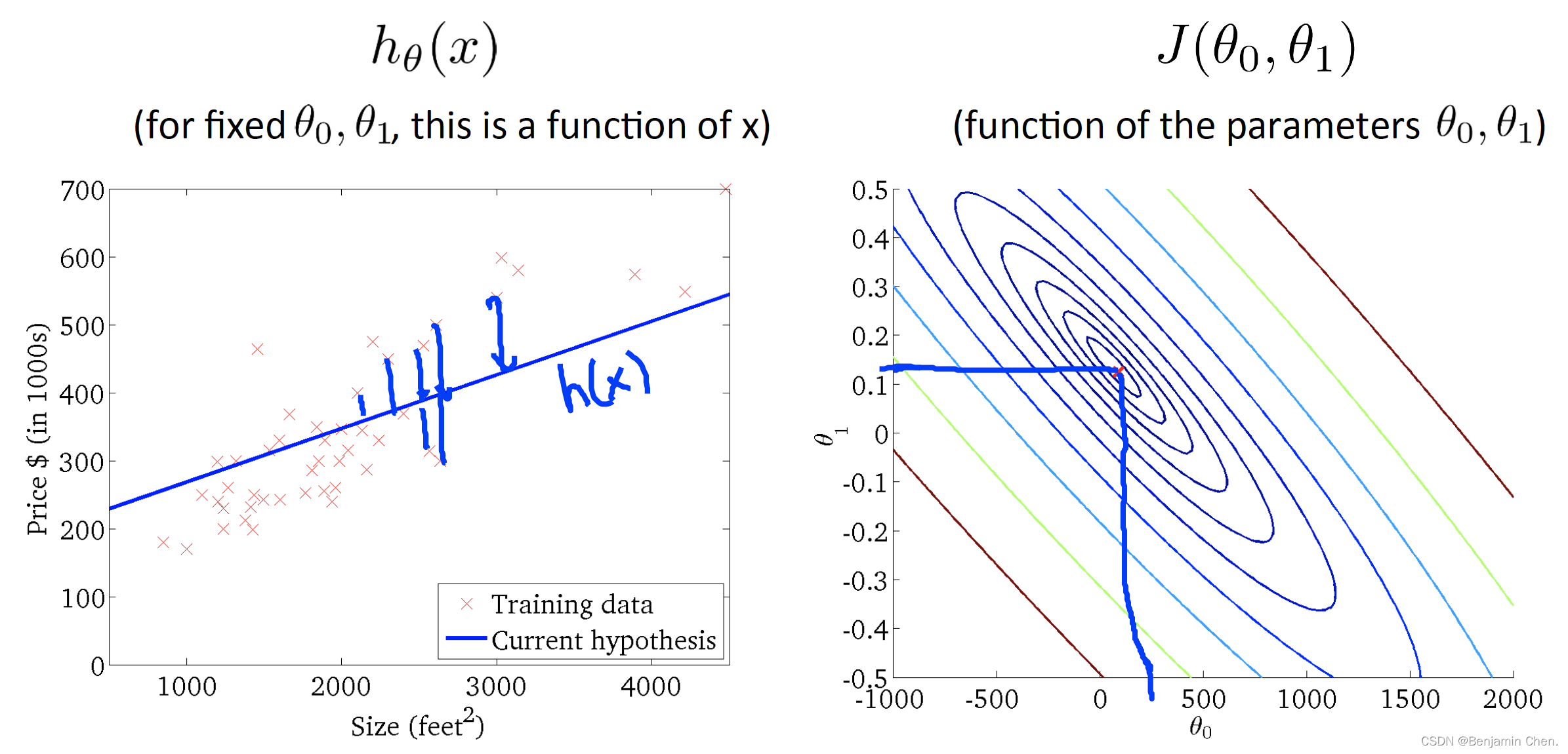
1.随着θ_0和θ_1的不断接近代价函数的中心,假设函数对数据的拟合越来越好