剑指offer-76、删除链表的节点

题⽬描述

给定单向链表的头指针和⼀个要删除的节点的值，定义⼀个函数删除该节点。返回删除后的链表的头节点。

此题对⽐原题有改动
题⽬保证链表中节点的值互不相同
该题只会输出返回的链表和结果做对⽐，所以若使⽤ C 或 C++ 语⾔，你不需要 free 或 delete 被删除的节点

数据范围:

0<=链表节点值<=10000
0<=链表⻓度<=10000

示例1

txt 复制代码

输⼊：{2,5,1,9},5
返回值：{2,1,9}
说明：给定你链表中值为 5 的第⼆个节点，那么在调⽤了你的函数之后，该链表应变为 2 -> 1 -> 9

示例2

txt 复制代码

输⼊：{2,5,1,9},1
返回值：{2,5,9}
说明：给定你链表中值为 1 的第三个节点，那么在调⽤了你的函数之后，该链表应变为 2 -> 5 -> 9

思路及解答

虚拟头节点

如果要删除链表⾥⾯的⼀个节点，其实就是将前置节点的next 直接指向当前节点的后置节点，这样在链表中再也找不到该节点了，也就是相当于删除了。

假设有⼀个链表，我们需要删除⾥⾯的 5 :

⾸先需要判断链表头结点是不是为空，如果为空，那么就直接返回NULL ，如果等于我们要找的，那么直接返回下⼀个节点引⽤即可。

如果不符合以上说的，那么我们需要新建⼀个前置节点pre ,与现在的链表连接在⼀起：

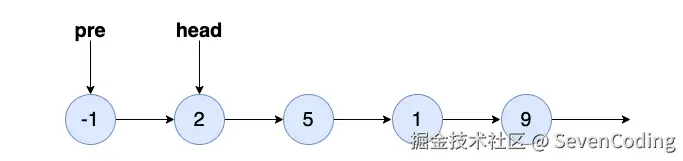
然后初始化⼀个 cur 节点表示当前节点，指向 head 节点：

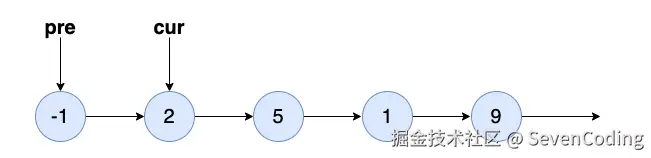
cur 不为空， cur 和 pre 后移：

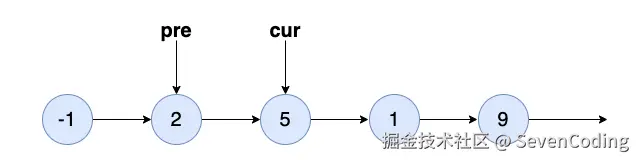
发现 cur 正是我们需要查找的 5 ，那么记录下 5 的下⼀个节点 1 ,也就是next :

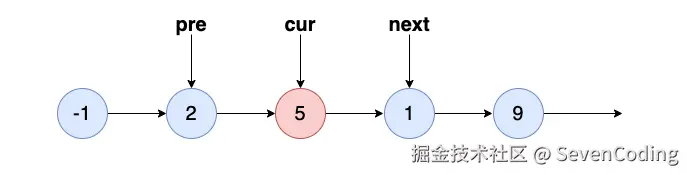
cur 的 next 指向 NULL ,使⽤ pre 的 next 指向刚刚记录的 next :

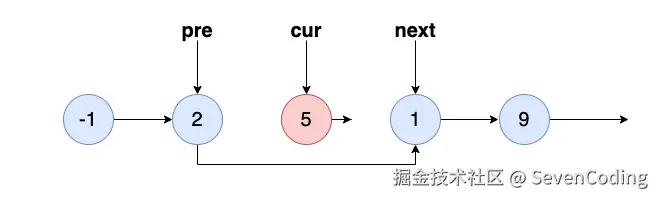
简化链表也就是：

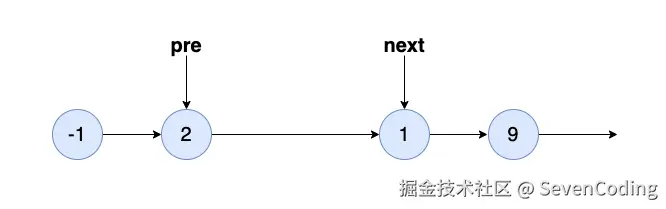
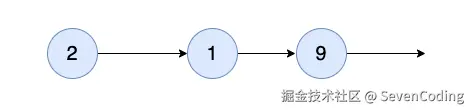
取之前虚拟的头结点的后⼀个节点，就是删除掉之后的新链表：

java 复制代码

class ListNode {
    int val;
    ListNode next = null;
    public ListNode(int val) {
    	this.val = val;
	}
}

public class Solution13 {
    public ListNode deleteNode(ListNode head, int val) {
        if (head == null) {
        	return null;
        }
        
        if (head.val == val) {
        	return head.next;
        }
        
        // ⽤⼀个节点将头结点链接起来
        ListNode pre = new ListNode(-1);
        pre.next = head;
        ListNode cur = head;
        ListNode next = null;
        while (cur != null) {
            if (cur.val == val) {
                // 将前置节点直接连接后⼀个节点，相当于删除掉了该节点
                pre.next = cur.next;
                break;
            }
            cur = cur.next;
            pre = pre.next;
        }
        return head;
    }
}

迭代

通过遍历链表找到目标节点并修改指针，维护前驱指针，当找到目标节点时修改指针跳过该节点

java 复制代码

public class Solution {
    public ListNode deleteNode(ListNode head, int val) {
        // 处理头节点就是要删除的节点的情况
        if (head != null && head.val == val) {
            return head.next;
        }
        
        ListNode prev = null;
        ListNode curr = head;
        
        // 遍历查找目标节点
        while (curr != null && curr.val != val) {
            prev = curr;
            curr = curr.next;
        }
        
        // 找到目标节点后跳过它
        if (curr != null) {
            prev.next = curr.next;
        }
        
        return head;
    }
}

时间复杂度：O(n)，最坏情况下需要遍历整个链表
空间复杂度：O(1)，只使用常数空间

递归

当前节点是要删除的节点则返回next，否则递归处理剩余链表

java 复制代码

public class Solution {
    public ListNode deleteNode(ListNode head, int val) {
        // 递归终止条件
        if (head == null) {
            return null;
        }
        
        // 当前节点是要删除的节点
        if (head.val == val) {
            return head.next;
        }
        
        // 递归处理剩余链表
        head.next = deleteNode(head.next, val);
        return head;
    }
}

时间复杂度：O(n)，需要处理每个节点
空间复杂度：O(n)，递归调用栈的深度