【机器学习】支持向量机

线性分类器，支持向量机

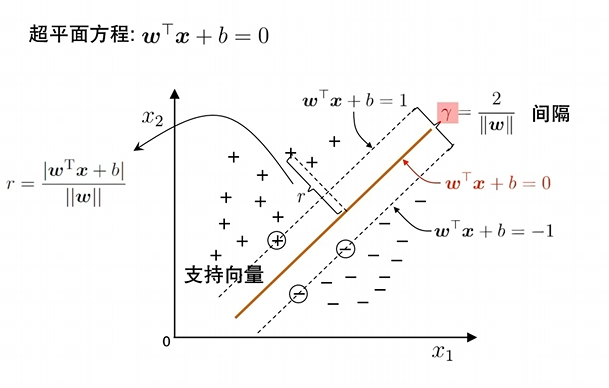
这张图片展示的是 支持向量机（Support Vector Machine, SVM） 的核心几何原理。SVM 的目标是找到一个"最胖"的红线（超平面），将两类数据完美分开。

我们可以对照图片中的标注，将这些数学公式和物理意义一一拆解：

1. 超平面方程：w⊤x+b=0w^\top x + b = 0w⊤x+b=0

这是中间那条红实线的数学描述。

xxx：代表数据点（比如图中的"+"和"-"）。
www （权重向量）：它垂直于红线，决定了红线的方向。
bbb（偏置）：决定了红线距离原点的位置。
在二维空间里，它其实就是我们熟悉的直线方程 Ax+By+C=0Ax + By + C = 0Ax+By+C=0 的向量写法。

2. 支持向量（Support Vectors）

注意图中被圆圈圈住的那三个点（两个"+"和一个"-"）。

它们是距离红线最近的"钉子户"。
SVM 的整个边界就是由这几个点"支撑"起来的。如果你移动其他远离红线的点，红线位置不会变；但如果你移动这几个支持向量，整个分类边界就会跟着动。

3. 间隔（Margin）：γ=2∥w∥\gamma = \frac{2}{\|w\|}γ=∥w∥2

这是 SVM 最核心的概念。图中两条虚线之间的距离被称为间隔。

两条虚线 ：方程分别是 w⊤x+b=1w^\top x + b = 1w⊤x+b=1 和 w⊤x+b=−1w^\top x + b = -1w⊤x+b=−1。
为什么是 2∥w∥\frac{2}{\|w\|}∥w∥2？ ：
- 单个点到直线的距离公式是 r=∣w⊤x+b∣∥w∥r = \frac{|w^\top x + b|}{\|w\|}r=∥w∥∣w⊤x+b∣。
- 对于虚线上的支持向量，其 ∣w⊤x+b∣|w^\top x + b|∣w⊤x+b∣ 正好等于 111。
- 所以，红线到单侧虚线的距离是 1∥w∥\frac{1}{\|w\|}∥w∥1，两侧总距离就是 2∥w∥\frac{2}{\|w\|}∥w∥2。
直观意义 ：为了让分类更稳健，我们希望这个间隔 γ\gammaγ 越大越好 。这等价于让 ∥w∥\|w\|∥w∥ 越小越好。

4. 点到平面的距离：r=∣w⊤x+b∣∥w∥r = \frac{|w^\top x + b|}{\|w\|}r=∥w∥∣w⊤x+b∣

图片左侧的这个公式解释了图中那条带箭头的细线 rrr。

它衡量的是空间中任意一个点 xxx 距离分类边界到底有多远。
在 SVM 的优化过程中，我们要求所有的"+"点 r≥正向间隔r \ge \text{正向间隔}r≥正向间隔，所有的"-"点 r≤负向间隔r \le \text{负向间隔}r≤负向间隔。

总结：SVM 在干什么？

SVM 其实是在做一个带约束的优化问题：

目标：最大化间隔 2∥w∥\frac{2}{\|w\|}∥w∥2（等价于最小化 12∥w∥2\frac{1}{2}\|w\|^221∥w∥2）。
约束：所有点都必须被正确分类，且落在间隔之外（即 yi(w⊤xi+b)≥1y_i(w^\top x_i + b) \ge 1yi(w⊤xi+b)≥1）。
这就是为什么我们之前提到拉格朗日乘子法 的原因------为了解这个带约束的优化方程，我们需要构造拉格朗日函数，利用支持向量来锁定最优的 www 和 bbb。

结合你上传的图片，我们现在将拉格朗日乘子法带入到 支持向量机（SVM） 的真实推导场景中。

SVM 的目标是找到一个超平面，在准确分类的同时，让间隔 γ=2∥w∥\gamma = \frac{2}{\|w\|}γ=∥w∥2 最大化。这在数学上等价于：

目标函数：min⁡w,b12∥w∥2\min_{w,b} \frac{1}{2}\|w\|^2minw,b21∥w∥2

约束条件：yi(w⊤xi+b)≥1,i=1,2,...,my_i(w^\top x_i + b) \ge 1, \quad i=1, 2, \dots, myi(w⊤xi+b)≥1,i=1,2,...,m

由于这里的约束是不等式（ $\\ge 1$ ），我们使用了扩展版的拉格朗日乘子法。

第一步：引入乘子，构建拉格朗日函数

图片显示，我们为每一个样本点 xix_ixi 都引入了一个拉格朗日乘子 αi≥0\alpha_i \ge 0αi≥0。

L(w,b,α)=12∥w∥2+∑i=1mαi(1−yi(w⊤xi+b))L(w, b, \alpha) = \frac{1}{2}\|w\|^2 + \sum_{i=1}^{m} \alpha_i \left( 1 - y_i(w^\top x_i + b) \right)L(w,b,α)=21∥w∥2+i=1∑mαi(1−yi(w⊤xi+b))

12∥w∥2\frac{1}{2}\|w\|^221∥w∥2：这是我们要最小化的"山谷"（能量最低点）。
∑αi(... )\sum \alpha_i (\dots)∑αi(...)：这是"惩罚项"。如果某个点违反了约束（跑到了间隔内），这一项就会产生很大的值。
注意符号 ：图片中将约束项写成了 (1−yi(... ))(1 - y_i(\dots))(1−yi(...))，这与标准的 f+λgf + \lambda gf+λg 是一致的。

第二步：求偏导，寻找"平衡点"

为了找到极值，我们需要让 LLL 对主变量 www 和 bbb 的偏导数为零。

对 www 求导：

∂L∂w=w−∑i=1mαiyixi=0\frac{\partial L}{\partial w} = w - \sum_{i=1}^m \alpha_i y_i x_i = 0∂w∂L=w−∑i=1mαiyixi=0

得到：w=∑i=1mαiyixiw = \sum_{i=1}^m \alpha_i y_i x_iw=∑i=1mαiyixi

物理意义 ：最终的最优超平面方向 www，实际上是由样本点 xix_ixi 的加权线性组合决定的。
对 bbb 求导：

∂L∂b=−∑i=1mαiyi=0\frac{\partial L}{\partial b} = -\sum_{i=1}^m \alpha_i y_i = 0∂b∂L=−∑i=1mαiyi=0

得到：∑i=1mαiyi=0\sum_{i=1}^m \alpha_i y_i = 0∑i=1mαiyi=0

物理意义：正负两类样本的"拉力"（乘子与标签的乘积）必须在偏移量上达到抵消平衡。

第三步：回代，得到"对偶问题"（Dual Problem）

这是图片中最复杂的一步。我们将上面求得的 www 代入到第一步的 LLL 函数中，消去 www 和 bbb，只剩下 α\alphaα。

通过繁琐的代数运算，问题转化为求 α\alphaα 的极大值：

max⁡α∑i=1mαi−12∑i=1m∑j=1mαiαjyiyjxi⊤xj\max_{\alpha} \sum_{i=1}^m \alpha_i - \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j x_i^\top x_jαmaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxi⊤xj

约束条件：∑αiyi=0\sum \alpha_i y_i = 0∑αiyi=0 且 αi≥0\alpha_i \ge 0αi≥0。

为什么要费这么大劲转化成第三步？

转化后的公式有一个惊人的发现：样本 xix_ixi 仅以"内积" xi⊤xjx_i^\top x_jxi⊤xj 的形式出现。

核技巧（Kernel Trick）：如果数据在当前维度分不开，我们可以把内积替换成"核函数"，从而在不计算高维坐标的情况下，直接在高维空间完成分类。这是 SVM 能够处理非线性问题的"神来之笔"。
稀疏性 ：解出来后你会发现，绝大多数 αi\alpha_iαi 都是 0。只有那些刚好踩在虚线边界上的点（支持向量），对应的 αi>0\alpha_i > 0αi>0。

总结

图片里的这个过程展示了数学如何将一个**"空间几何问题"通过拉格朗日乘子法，转化成一个"只跟样本之间相似度（内积）有关的代数问题"**。

这就像是：我们不需要知道整座山的形状，只需要通过几个关键点（支持向量）之间的相互作用力，就能锁定最完美的隔离墙。

既然你已经看完了推导，想了解一下为什么最后这个公式里 xi⊤xjx_i^\top x_jxi⊤xj 的出现，能让我们用"核函数"来降维打击复杂问题吗？

求解方法SMO

你提供的图片展示了 SMO (Sequential Minimal Optimization，序列最小优化算法) 的核心逻辑。它是为了解决 SVM 的对偶问题（Dual Problem）而发明的，由 John Platt 在 1998 年提出。

既然你前面已经看懂了拉格朗日乘子法，那理解 SMO 就只差临门一脚了。

1. 核心原理：为什么要同时选两个 α\alphaα？

在 SVM 的对偶问题中，我们有这样一个硬性约束：
∑i=1mαiyi=0\sum_{i=1}^{m} \alpha_i y_i = 0i=1∑mαiyi=0

如果只更新一个 αi\alpha_iαi ：比如你改变了 α1\alpha_1α1，为了让等式依然等于 0，你没法动，因为其他 α\alphaα 都被固定了。这就像天平，你动了左边的一个砝码，如果不准动别的砝码，天平就永远平不了。
所以必须同时选两个：改变 αi\alpha_iαi 的同时，对应地改变 αj\alpha_jαj，使得：
αiyi+αjyj=常数 c\alpha_i y_i + \alpha_j y_j = \text{常数 } cαiyi+αjyj=常数 c

这样就能在保证"天平平衡"（满足约束）的前提下，去优化目标函数。

2. SMO 的执行步骤

SMO 将一个巨大的优化问题拆解成了无数个极其简单的子问题：

第一步：选取变量对 (αi,αj)(\alpha_i, \alpha_j)(αi,αj)

并不是随便选两个

第一个变量 αi\alpha_iαi ：通常选择违背 KKT 条件最严重的那个样本。也就是说，这个点本来应该是支持向量但模型没把它算对，或者它本不该是支持向量却占了位置。
第二个变量 αj\alpha_jαj：选择那个能让目标函数值改变最大的变量。

第二步：求解闭式解（关键）

由于只有两个变量，原来的二次规划问题就变成了一个一元二次方程 （因为 αj\alpha_jαj 可以用 αi\alpha_iαi 表示）。

方程的图像是一个开口向下的抛物线。
我们直接求导就能算出 αj\alpha_jαj 的新值。
剪辑（Clipping） ：算出的新 αj\alpha_jαj 必须满足 0≤α≤C0 \le \alpha \le C0≤α≤C 的范围（如果是硬间隔 SVM，则是 α≥0\alpha \ge 0α≥0）。如果算出来超标了，就强行把它拉回到边界上。

3. 举例说明

假设我们有 3 个样本，标签分别是 y1=1,y2=−1,y3=1y_1=1, y_2=-1, y_3=1y1=1,y2=−1,y3=1。当前状态下：
α1=1,α2=1,α3=0\alpha_1=1, \alpha_2=1, \alpha_3=0α1=1,α2=1,α3=0。

检查约束：1(1)+1(−1)+0(1)=01(1) + 1(-1) + 0(1) = 01(1)+1(−1)+0(1)=0。符合要求。

启动 SMO ：我们发现模型对样本 1 和样本 2 的分类不够好，决定优化 α1,α2\alpha_1, \alpha_2α1,α2。
锁定约束 ：此时 α1y1+α2y2=1−1=0\alpha_1 y_1 + \alpha_2 y_2 = 1 - 1 = 0α1y1+α2y2=1−1=0。这意味着在后续优化中，必须保证 α1−α2=0\alpha_1 - \alpha_2 = 0α1−α2=0，即 α1=α2\alpha_1 = \alpha_2α1=α2。
代入目标函数 ：把所有的 α1\alpha_1α1 都换成 α2\alpha_2α2，原来的复杂函数就变成了关于 α2\alpha_2α2 的简单二次函数 f(α2)=Aα22+Bα2+Cf(\alpha_2) = A\alpha_2^2 + B\alpha_2 + Cf(α2)=Aα22+Bα2+C。
求极值 ：求导发现 α2\alpha_2α2 取 1.51.51.5 时函数值最大。
更新：于是 α2new=1.5\alpha_2^{new} = 1.5α2new=1.5。根据约束，α1new\alpha_1^{new}α1new 也必须是 1.51.51.5。
检查：新的 α\alphaα 组合满足约束且让目标函数更优。接着去挑下一对 α\alphaα。

4. 关于偏置 bbb 的更新

图片最后提到：对于任意支持向量 (xs,ys)(x_s, y_s)(xs,ys)，都有 ysf(xs)=1y_s f(x_s) = 1ysf(xs)=1。

因为支持向量正好踩在那个"1"或者"-1"的虚线上。
每更新一对 α\alphaα，我们都会利用这个性质重新算一下 bbb。
为了鲁棒性，我们会把所有支持向量算出的 bbb 取个平均值。

总结：为什么 SMO 这么快？

不用矩阵运算：传统的二次规划需要解大型矩阵，极慢。SMO 每次只算两个数，是解析解（闭式解），速度极快。
内存占用低：不需要存储巨大的核矩阵。
收敛快 ：虽然选取的对数很多，但每一对的计算几乎瞬间完成。
简单说，SMO 就是把"全局大修"变成了"局部微调"，每次只调两个参数，调准了再换下一对，直到全场都调稳为止。

特征空间映射

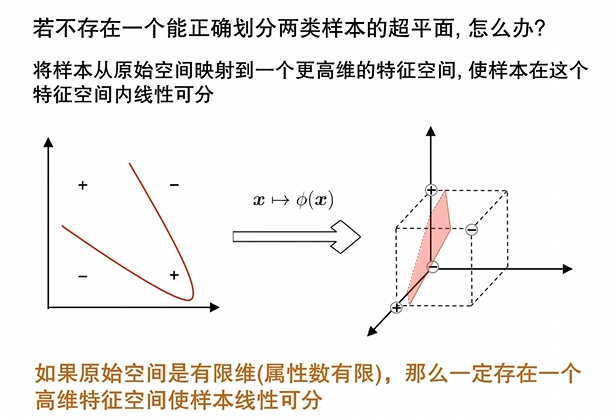
在特征空间中

核函数

在支持向量机（SVM）的推导中，你已经看到了公式最后出现了 xi⊤xjx_i^\top x_jxi⊤xj。核函数（Kernel Function） 的出现，就是为了把这个简单的内积变成一个"超能力"，让 SVM 能够处理那些在原始空间里根本分不开的数据。

简单来说，核函数就是："在低维空间计算，达到高维空间的效果。"

1. 核心动机：为什么要"升维"？

想象桌子上混杂着红豆和绿豆，你无法用一根直尺（线性分类器）把它们分开。但如果你拍一下桌子，让豆子飞到空中，在豆子飞起的瞬间，你可能就能用一张纸（平面）从中间把它们隔开。

低维不可分：在原始特征空间（比如二维），数据可能是扭曲、环绕的，无法用直线分开。
高维线性可分 ：根据 Cover 定理，将复杂的样本特征映射到更高维的空间，样本变得线性可分的概率就会大幅提高。

2. 什么是"核技巧"（Kernel Trick）？

如果我们要把数据映射到高维空间 ϕ(x)\phi(x)ϕ(x)，通常的做法是：

先算高维坐标 ϕ(xi)\phi(x_i)ϕ(xi) 和 ϕ(xj)\phi(x_j)ϕ(xj)。
再算它们的内积 ϕ(xi)⊤ϕ(xj)\phi(x_i)^\top \phi(x_j)ϕ(xi)⊤ϕ(xj)。
问题在于 ：如果维度非常高（甚至是无限维），计算 ϕ(x)\phi(x)ϕ(x) 的坐标会耗尽计算机内存。
核函数的妙处：它定义了一个函数 K(xi,xj)K(x_i, x_j)K(xi,xj)，使得：

K(xi,xj)=ϕ(xi)⊤ϕ(xj)K(x_i, x_j) = \phi(x_i)^\top \phi(x_j)K(xi,xj)=ϕ(xi)⊤ϕ(xj)

这意味着：你不需要知道高维空间的坐标是什么，你只需要在低维空间代入公式算一个数，这个数就等价于它们在高维空间里的内积。

3. 常见的核函数

在实际应用中，我们不需要自己发明映射函数，通常使用以下几种成熟的核：

核函数名称	公式表达式	特点与应用
线性核 (Linear)	K(xi,xj)=xi⊤xjK(x_i, x_j) = x_i^\top x_jK(xi,xj)=xi⊤xj	不升维，适用于特征非常多（如文本分类）的情况。
多项式核 (Polynomial)	K(xi,xj)=(xi⊤xj+c)dK(x_i, x_j) = (x_i^\top x_j + c)^dK(xi,xj)=(xi⊤xj+c)d	显式地考虑特征之间的组合，如 x1x2x_1x_2x1x2。
高斯核 (RBF/Gaussian)	KaTeX parse error: Expected group after '^' at position 41: ...a \\|x_i - x_j\\|^̲	最常用。能将数据映射到无限维空间。γ\gammaγ 越大，模型越复杂。
Sigmoid 核	K(xi,xj)=tanh⁡(βxi⊤xj+θ)K(x_i, x_j) = \tanh(\beta x_i^\top x_j + \theta)K(xi,xj)=tanh(βxi⊤xj+θ)	让 SVM 的表现类似于一个简单的神经网络。

4. 结合你之前的 SMO 图片

看你上传的第三张图片（拉格朗日第三步），那个对偶问题的目标函数：
max⁡α∑i=1mαi−12∑i=1m∑j=1mαiαjyiyj(xi⊤xj)\max_{\alpha} \sum_{i=1}^m \alpha_i - \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j (x_i^\top x_j)αmaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyj(xi⊤xj)

如果你使用了核函数，你只需要把括号里的 (xi⊤xj)(x_i^\top x_j)(xi⊤xj) 换成 K(xi,xj)K(x_i, x_j)K(xi,xj)。

SMO 算法完全不需要改动，它只是在计算过程中查了一下"核函数表"。
最终得到的分类决策函数也变成了：
f(x)=∑i=1mαiyiK(xi,x)+bf(x) = \sum_{i=1}^m \alpha_i y_i K(x_i, x) + bf(x)=i=1∑mαiyiK(xi,x)+b

5. 总结

核函数是 SVM 的灵魂，它解决了两个矛盾：

分类能力的矛盾：通过升维解决非线性分类问题。
计算效率的矛盾：通过"内积等价"避免了直接处理高维坐标的巨大开销。

比喻：核函数就像是一个"翻译官"。它不需要把你带到那个复杂的维度去，它直接告诉你两个点在那个维度里的"亲密度"（内积）是多少。