最近在整理机器学习的代码以及加强对机器学习的理解，于是按照自己的理解花了一周的时间整理了这篇博客，以便于后续的回顾和交流。后续所演示的实例是基于回归分析的。
目录
[1. 前言](#1. 前言)
[2. 多层感知器（MLP）](#2. 多层感知器（MLP）)
[2.1 输入层](#2.1 输入层)
[2.2 隐藏层](#2.2 隐藏层)
[2.3 输出层](#2.3 输出层)
[2.4 权重](#2.4 权重)
[2.5 偏置神经元](#2.5 偏置神经元)
[2.6 激活函数](#2.6 激活函数)
[2.7 前馈和反向传播](#2.7 前馈和反向传播)
[3. MLP结构示意图](#3. MLP结构示意图)
[4. 方法](#4. 方法)
[4.1 随机梯度下降（SGD）](#4.1 随机梯度下降（SGD）)
[4.1.1 计算过程](#4.1.1 计算过程)
[4.2 反向传播](#4.2 反向传播)
[5. MLP 建模前必须做的数据预处理](#5. MLP 建模前必须做的数据预处理)
[5.1 特征尺度统一](#5.1 特征尺度统一)
[5.2 缺失值处理](#5.2 缺失值处理)
[5.3 异常值处理（尤其是回归问题）](#5.3 异常值处理（尤其是回归问题）)
[6. MLP 案例演示(回归)](#6. MLP 案例演示(回归))
[Sklearn 官方建议](#Sklearn 官方建议)
[7. 参考文献](#7. 参考文献)
[8. 代码区](#8. 代码区)
1. 前言
机器学习是人工智能的分支，深度学习是机器学习的一部分。
人工智能（AI）
└── 机器学习（ML）
├── 传统机器学习（RF / SVM / KNN / XGBoost）
└── 深度学习（DL）
├── MLP
├── CNN
├── RNN / LSTM
└── Transformer
神经网络或人工神经网络是机器学习中的基本工具，神经网络由相互连接的节点（称为神经元）组成，这些节点被组织成不同的层。每个神经元接收输入信号，使用激活函数对其进行计算，并产生一个输出信号，该输出信号可以传递给网络中的其他神经元。激活函数决定了神经元根据其输入所得到的输出。这些函数为网络引入了非线性，使其能够学习数据中的复杂模式。该网络通常由多层组成，首先是输入层，用于输入数据；然后是隐藏层，用于执行计算；最后是输出层，用于做出预测或决策。
相邻层中的神经元通过加权相互连接，从而将信号从一层传递到下一层。这些连接的强度（由权重表示）决定了一个神经元的输出对另一个神经元的输入的影响程度。在训练过程中，网络会根据训练数据集调整其权重。此外，每个神经元通常都有一个相关的偏置，用于调整其输出阈值。
神经网络的训练采用前馈传播和反向传播两种技术。在前馈传播过程中，输入数据逐层传递到网络中，每一层都根据接收到的输入进行计算，并将结果传递给下一层。反向传播算法是一种用于训练神经网络的算法，它通过迭代地调整网络的权重和偏置来最小化损失函数。损失函数（也称为成本函数或目标函数）衡量模型预测值与训练数据中真实目标值匹配程度的指标。损失函数量化了模型预测输出与实际输出之间的差异，为训练过程中的优化提供指导。
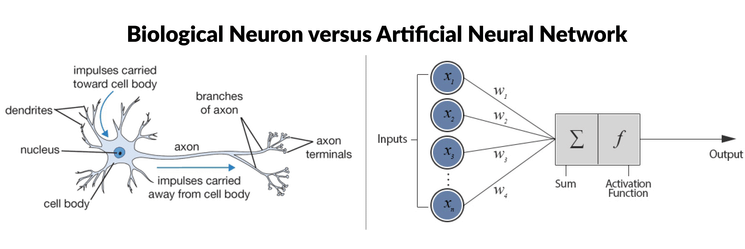生物神经元与人工神经网络*（来源：ResearchGate和Multilayer Perceptrons in Machine Learning: A Comprehensive Guide）*
人工神经网络（ANN）有很多类型，最基础的为前馈神经网络(FNN)，循环神经网络，卷积神经网络等等。。。。
2. 多层感知器（MLP）
而多层感知器是一种前馈神经网络，由具有非线性激活函数的全连接神经元组成。它广泛用于区分非线性可分的数据。结构简单，通用性强，多适合于表格数据和低纬度的特征回归或分类问题。
2.1 输入层
输入层由接收初始输入数据的节点或神经元组成。每个神经元代表输入数据的一个特征或维度。输入层中神经元的数量取决于输入数据的维度。
2.2 隐藏层
输入层和输出层之间可以有一层或多层神经元。隐藏层中的每个神经元接收来自前一层（输入层或其他隐藏层）所有神经元的输入，并产生一个输出，该输出传递到下一层。隐藏层的数量以及每个隐藏层中的神经元数量都是超参数，需要在模型设计阶段确定。
2.3 输出层
这一层由产生网络最终输出的神经元组成。输出层中神经元的数量取决于任务的性质。在二分类任务中，根据激活函数的不同，输出层可能只有一个或两个神经元，分别代表属于某一类别的概率；而在多分类任务中，输出层可以有多个神经元。
2.4 权重
相邻层中的神经元彼此完全连接。每个连接都有一个相关的权重，该权重决定了连接的强度。这些权重在训练过程中学习得到。权重决定了这个神经元重不重要，权重大，则影响大，反之亦然。
2.5 偏置神经元
除了输入层和隐藏层神经元之外，每一层（输入层除外）通常都包含一个偏置神经元，它为下一层神经元提供一个恒定的输入。偏置神经元的每个连接都有其自身的权重，该权重也在训练过程中学习得到。
偏置神经元有效地改变了后续层神经元的激活函数，使网络能够学习决策边界的偏移量或偏差。通过调整与偏置神经元相连的权重，多层感知器（MLP）可以学习控制激活阈值，从而更好地拟合训练数据。类似于线性回归y=ax+b中 的b（截距）。
**注意：**在多层感知器（MLP）的语境下，偏差可以指代两个相关但不同的概念：机器学习中的通用术语"偏差"和上文定义的偏差神经元。在一般机器学习中，偏差指的是用简化模型近似实际问题时引入的误差。偏差衡量模型捕捉数据中潜在模式的能力。高偏差表明模型过于简单，可能无法很好地拟合数据；而低偏差则表明模型能够很好地捕捉潜在模式。
2.6 激活函数
通常，隐藏层和输出层中的每个神经元都会对其输入的加权和应用一个激活函数。常见的激活函数包括 sigmoid、tanh、ReLU（修正线性单元）和 softmax。这些函数为网络引入了非线性，使其能够学习数据中的复杂模式。激活函数的目的是为了打断线性链接，他把神经元的输出结果比作了一个警报器，小的声音压住，大的声音开始警报
2.7 前馈和反向传播
MLP 使用反向传播算法进行训练，该算法计算损失函数相对于模型参数的梯度，并迭代地更新参数以最小化损失。
3. MLP结构示意图
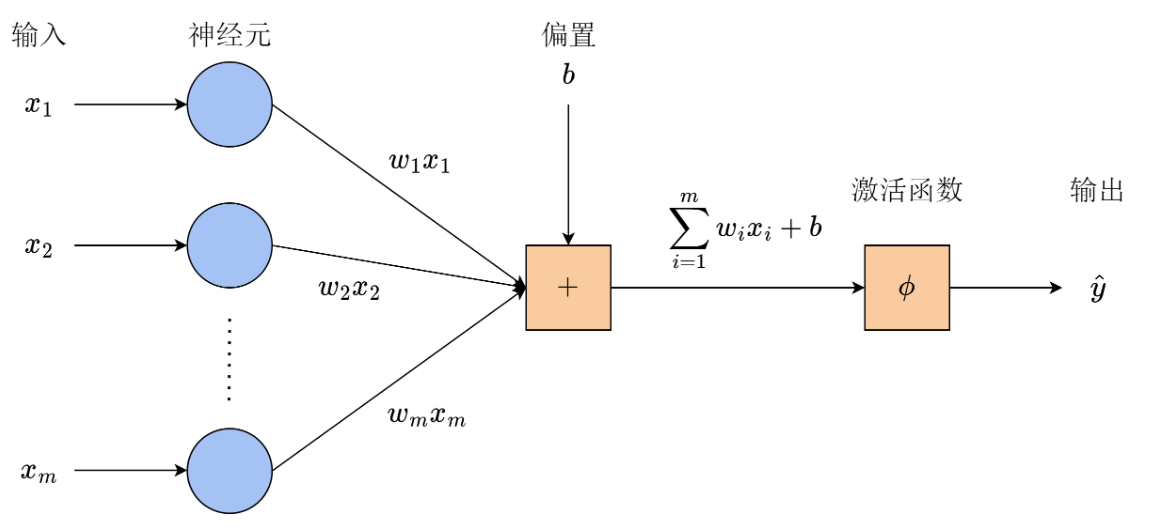感知机结构 （图片来源：第 8 章 神经网络与多层感知机 ）
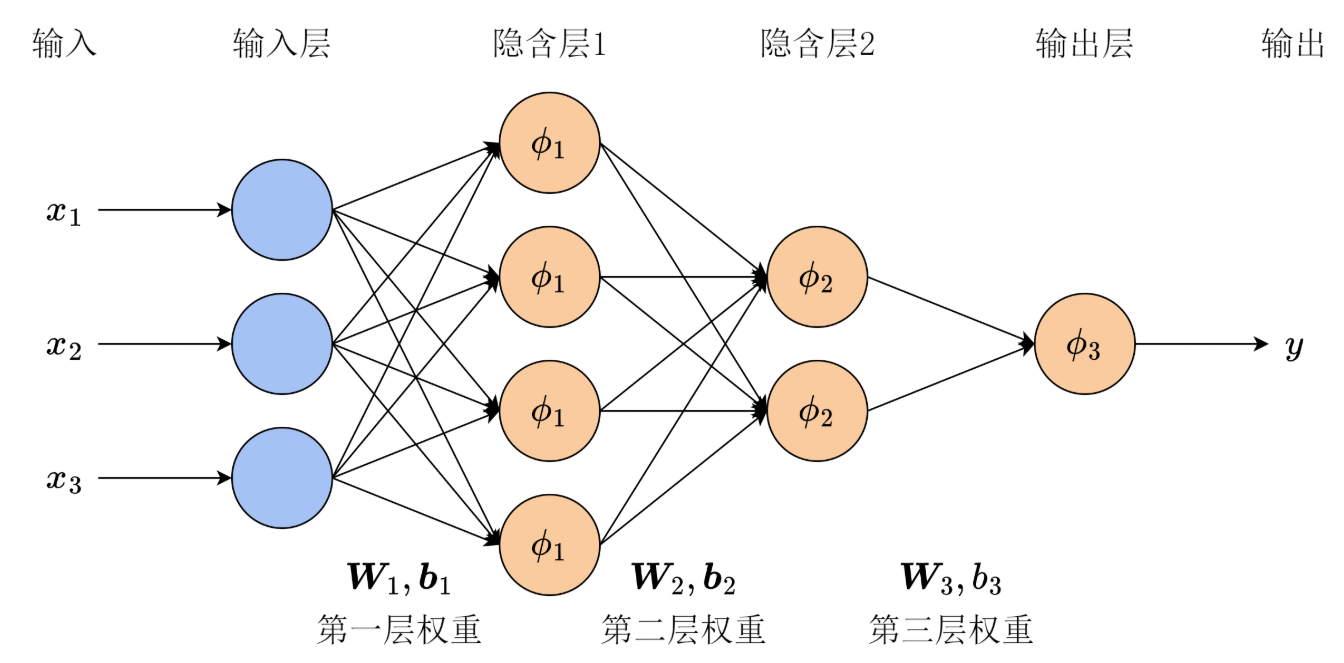三层的MLP运算过程（图片来源：第 8 章 神经网络与多层感知机）
4. 方法
在训练过程中，神经网络会学习调整每个神经元输入的权重，以最小化预测输出与训练数据中真实目标值之间的差异。通过调整权重并学习合适的激活函数，神经网络能够近似地识别数据中复杂的模式和关系，从而对新的、未见过的样本做出准确的预测。这种调整由优化算法指导，例如随机梯度下降（SGD），它计算损失函数相对于权重的梯度，并迭代地更新权重。
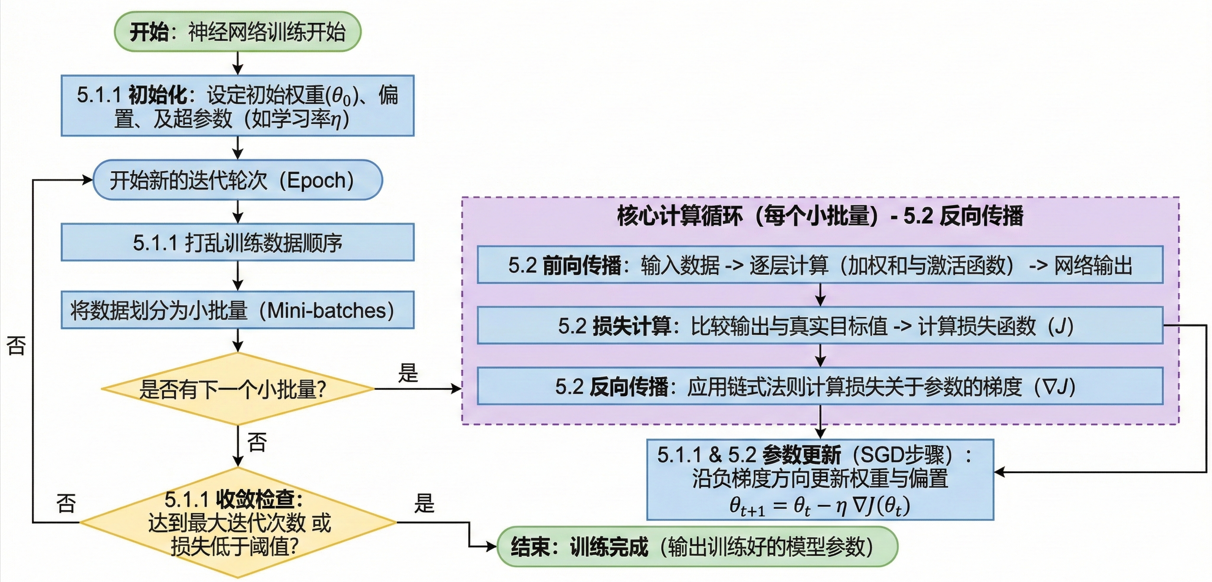
基于随机梯度下降和反向传播的神经网络训练框架（图片来源于：Nano Banana Pro）
4.1 随机梯度下降（SGD）
随机梯度下降法（Stochastic Gradient Descent，SGD）是一种用于优化模型参数的迭代算法 ，核心作用是：
通过不断减小损失函数，使模型预测结果越来越接近真实值。
这里参考了ChatGPT的解释："SGD 就是：不等把所有样本都算一遍，而是每次随机抽一小部分样本，立刻沿着"误差下降最快的方向"更新模型参数。"
4.1.1 计算过程
- 初始化： SGD 从随机或使用一些预定义的方法开始，以一组初始模型参数（权重和偏差）开始。
- 迭代优化： 此步骤的目标是通过迭代地沿着损失函数值下降最快的方向移动，找到损失函数的最小值。对于训练的每次迭代（或轮次）：
- 对训练数据进行打乱顺序，以确保模型不会每次都从相同的模式和顺序中学习。
- 将训练数据分成小批量（数据的小子集）。
- 每个小批量：
- 仅使用小批量数据点计算损失函数关于模型参数的梯度。该梯度估计是对真实梯度的随机近似。
- 通过沿梯度相反方向更新模型参数，步长乘以学习率：θₜ₊₁ = θₜ − η ∇J(θₜ) 其中：
θₜ表示第 t 次 迭代时的模型参数（例如，权重和偏差）。∇J(θₜ)是损失函数在第t 次J迭代时关于参数的梯度。η(eta) 是学习率，它控制优化过程中的步长。
- **下降方向：**损失函数的梯度指示了最陡上升的方向。为了最小化损失函数，梯度下降法会沿相反方向移动，即朝着最陡下降的方向移动。
- 学习率： 梯度下降算法每次迭代的步长由一个称为学习率的参数决定，如上所示
n。该参数控制着算法向最小值迈出的步长。如果学习率太小，收敛速度可能会很慢；如果学习率太大，算法可能会出现振荡或发散。 - **收敛：**重复该过程固定次数的迭代，或者直到满足收敛标准（例如，损失函数的变化低于某个阈值）。
随机梯度下降法利用较小的数据子集更频繁地更新模型参数，因此计算效率很高，尤其适用于大型数据集。随机梯度下降法引入的随机性可以起到正则化作用，防止模型过拟合训练数据。它也非常适合在线学习场景，因为新数据是逐步增加的，而随机梯度下降法能够利用每个新数据点或小批量数据快速更新模型。
然而，随机梯度下降法（SGD）也存在一些挑战，例如由于梯度估计的随机性而导致的噪声增加，以及需要调整学习率等超参数。为了应对这些挑战并提高收敛性和性能，人们开发了多种SGD的扩展和改进方法，例如小批量随机梯度下降法、动量法以及自适应学习率方法，如AdaGrad、RMSProp和Adam。
4.2 反向传播
反向传播是"误差反向传播"的简称。反向传播是一种计算神经网络中每个参数"该往哪个方向、改多少"的方法，用来指导模型如何更新权重以减小预测误差。在反向传播的背景下，随机梯度下降（SGD）算法会根据每个训练批次计算出的梯度，迭代地更新网络参数。SGD 算法并非使用整个训练数据集来计算梯度（对于大型数据集来说，计算成本可能很高），而是使用称为小批量的随机数据子集来计算梯度。以下是反向传播算法的工作原理概述：
- **前向传播：**在前向传播过程中，输入数据被送入神经网络，网络的输出逐层计算。每个神经元计算其输入的加权和，对结果应用激活函数，并将输出传递给下一层的神经元。
- **损失计算：**经过前向传播后，将网络的输出与真实目标值进行比较，并计算损失函数来衡量预测输出与实际输出之间的差异。
- **反向传播（梯度计算）：**在反向传播过程中，利用链式法则计算损失函数相对于网络参数（权重和偏置）的梯度。梯度表示损失函数相对于每个参数的变化率，并提供有关如何调整参数以降低损失的信息。
- **参数更新：**梯度计算完成后，为了最小化损失函数，网络参数会沿梯度的反方向进行更新。这种更新通常使用优化算法来实现，例如我们之前讨论过的随机梯度下降（SGD）。
- **迭代过程：**步骤 1-4 重复执行，直至达到预设的迭代次数或满足收敛准则。每次迭代中，网络参数会根据反向传播计算出的梯度进行调整，从而逐步降低损失并提升模型性能。
5. MLP 建模前必须做的数据预处理
5.1 特征尺度统一
MLP 通过梯度下降训练，对特征尺度极其敏感。
如果不做尺度统一：
-
大尺度特征主导梯度
-
小尺度特征几乎不起作用
-
收敛慢，甚至不收敛
常用方法（任选其一）：
-
标准化（最常用）：减去特征的均值在除于特征的标准差，这样可以将数据中心化到零，并其方差趋于1。
-
归一化（0--1）
但是根据Datacamp. (2025)报道
- 标准化和归一化之间的选择可能取决于多层感知器（MLP）中使用的激活函数。像 sigmoid 和 tanh 这样的激活函数对输入数据的尺度很敏感，因此可能需要进行标准化。另一方面，像 ReLU 这样的激活函数对尺度不太敏感，可能不需要进行标准化。
但是为了确保建模的精度，还是建议使用标准化预处理数据
5.2 缺失值处理
MLP 不能直接处理缺失值。
必须：
-
删除样本（样本量足够时）
-
或插值 / 均值 / KNN 填补
5.3 异常值处理（尤其是回归问题）
处理方式： IQR 或Z-score
6. MLP 案例演示(回归)
本次实验所使用的768个样本来源于
By A. Tsanas, Angeliki Xifara. 2012
Published in Energy and Buildings, vol. 49
DOI
数据集中各变量的含义为:
X1 Relative Compactness
X2 Surface Area
X3 Wall Area
X4 Roof Area
X5 Overall Height
X6 Orientation
X7 Glazing Area
X8 Glazing Area Distribution
y1 Heating Load
- 输入数据
- 得到训练结果
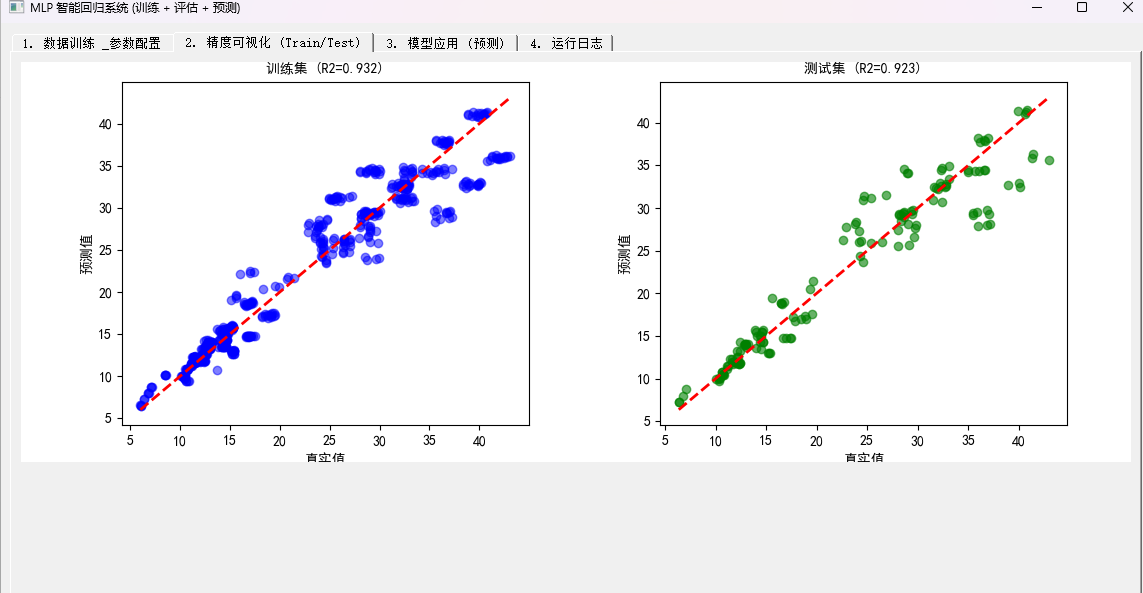
在构建的代码中，并没有使用随机梯度下降，究其原因是样本量太少（500+），若是只用sgd，那么他的收敛速度会很慢，模型震荡严重。
Sklearn 官方建议
scikit-learn 的官方文档中明确指出：
"For small datasets, 'lbfgs' can converge faster and perform better." (对于小数据集，'lbfgs' 收敛更快且表现更好。)
"For large datasets, 'adam' or 'sgd' are more efficient." (对于大数据集，'adam' 或 'sgd' 更有效。)
7. 参考文献
【1】Leshno, M., Lin, V. Y., Pinkus, A., & Schocken, S. (1993).Multilayer feedforward networks with a nonpolynomial activation function can approximate any function.Neural Networks, 6(6), 861--867.https://doi.org/10.1016/S0893-6080(05)80131-5
8. 代码区
用于回归的代码链接：https://download.csdn.net/download/2301_77490282/92657058
用于分类的代码链接可以参考这篇博客：深度学习02-神经网络(MLP多层感知器)