目标定的数学推导链条:
从点的匹配 → 基础矩阵 F → 本质矩阵 E → 分解得到 R, T。
内容是数学推导 + 工程注意点,是视觉几何最核心部分。
1、整体流程(一张图看懂)
匹配点对
→ 解 基础矩阵 F
→ 用内参去掉像素坐标影响得到 本质矩阵 E = Kᵀ F K
→ 对 E 做 SVD 分解
→ 由 E 提取出两个旋转 R 和一个平移方向 T
→ 根据三角化取正确解(4 种组合取唯一物理解)
1. 从点匹配到基础矩阵 F(Fundamental Matrix)
给定多组同名点:

1. 极线约束来自极平面
任意 3D 点 X 在两个相机中成像为 x₁, x₂:
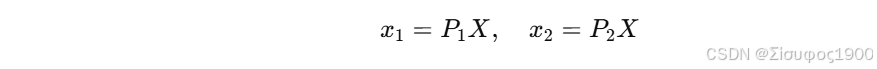
极平面经过 C1、C2 和 X,导致 x₁, x₂, T 三向量共面:
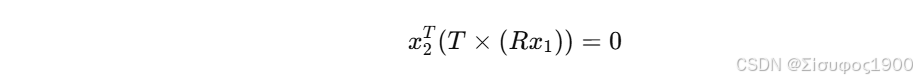
这正是极线约束。
2. DLT 八点法构建 F
对点对 (x1,x2)
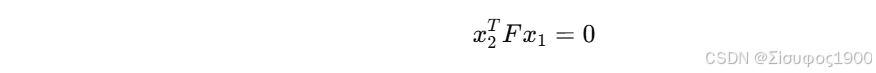
展开得线性方程:
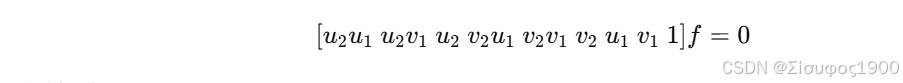
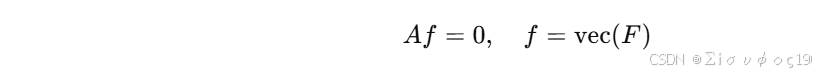
通过 SVD 最小奇值对应向量 得到 F,再强制 rank=2。
cpp
function F = eight_point_F(pts1, pts2)
% pts1, pts2: Nx2 对应点坐标 (N>=8)
% --- 1. 归一化 ---
[pts1_n, T1] = normalizePoints(pts1);
[pts2_n, T2] = normalizePoints(pts2);
N = size(pts1_n,1);
x1 = pts1_n(:,1); y1 = pts1_n(:,2);
x2 = pts2_n(:,1); y2 = pts2_n(:,2);
% --- 2. 构建 A ---
A = [x2.*x1, x2.*y1, x2, ...
y2.*x1, y2.*y1, y2, ...
x1, y1, ones(N,1)];
% --- 3. SVD 求 f ---
[~,~,V] = svd(A);
F_n = reshape(V(:,end), 3,3)';
% --- 4. rank-2 约束 ---
[U,S,V] = svd(F_n);
S(3,3) = 0;
F_n = U * S * V';
% --- 5. 反归一化 ---
F = T2' * F_n * T1';
end
function [pts_n, T] = normalizePoints(pts)
centroid = mean(pts,1);
pts_c = pts - centroid;
dist = mean(sqrt(sum(pts_c.^2,2)));
s = sqrt(2) / dist;
T = [s 0 -s*centroid(1);
0 s -s*centroid(2);
0 0 1];
pts_h = [pts, ones(size(pts,1),1)]';
pts_n_h = T * pts_h;
pts_n = pts_n_h(1:2,:)' ;
end
cpp
% 随机 8 对点
pts1 = rand(8,2) * 1000;
pts2 = rand(8,2) * 1000;
F = eight_point_F(pts1, pts2)
2. 由 F 得到本质矩阵 E
像素点满足 F,但 F 受到相机内参与像素坐标的影响。
而两相机在 归一化相机坐标系 下满足:
归一化坐标:
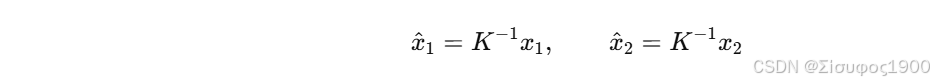
带人到极线约束中
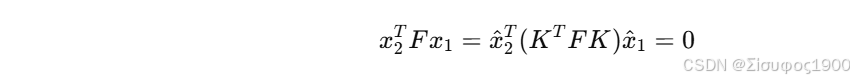
所以本质矩阵为:
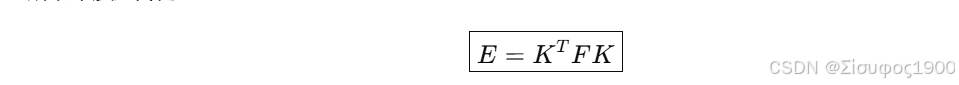

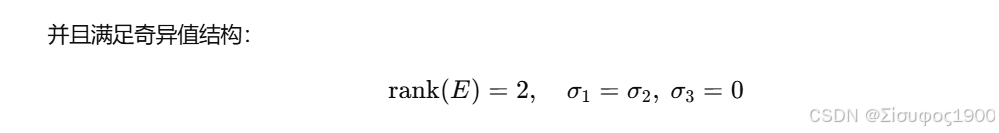
3. 本质矩阵 E 的结构特点
E 的理想结构:

4. 分解 E:SVD
对 E 做 SVD:

5. 提取旋转矩阵 R

6. 提平移方向 T

即 U 的第三列(对应零奇异值)是平移方向。
注意:
T 只有 方向,没有尺度(基线长度无法从图像求得)。
7. 四种组合(4 solutions)

8. 选出正确解:三角化(正深度约束)


总结:
✔ Step1. 八点法求 F
线性最小二乘 + rank2
✔ Step2. E = Kᵀ F K
将像素约束转成归一化坐标
✔ Step3. E = [T]× R
极平面几何必然给出