《智能的理论》全书转至目录****
不同AGI的研究路线对比简化版:《AGI(具身智能)路线对比》,欢迎各位参与讨论、批评或建议。
第6节 数
数是人类的基本能力(如果没有数就无法交易,一切工程活动也无法进行等),在许多动物如灵长类、狗、小鸡、甚至是蜜蜂也发现了数的能力。数之所以具有生物普遍性,是因为数在生物的演化过程中具有积极作用,如通过判断树上可食用植物的数量,便可前往食物更充足的区域;水塘中知觉到食肉动物的数量,鱼群会进入更大的池塘以减少被吃的风险;蜜蜂计算花瓣的数量以识别花朵种类。
环境中的数有两种表现形式,一种是非符号数量形式,即通过场景客体所表现出来的数量,如两个苹果、两只老虎、三个点、五个声音、十一次敲打等等。我们有从环境中提取这种非符号数量的能力;另外一种是符号信息,如阿拉伯数字"2"或者中文数字"二"等等。(毛伙敏,刘琴,吕建相和牟毅,2021)
一.概念量级(刘文莉,2022)
1.定义
个体在观察一个物体时,通常包含了两个维度的大小,一个来自内在特征,概念量级即是对物体的内部物理大小的表示;另一个来自表面特征,物理量级即是对物体表面的感知大小(Gliksman,Itamir,Leibovitzich和Melan等人,2016)。关于概念量级和物理量级的关系,有研究认为概念量级是对物理量级的心理表征(Paivio,1978),可以传递物体具体的量级信息,例如,人们知道"狮子"比"蚂蚁"大,即使仅仅看到概念词而没有看到真实物体,也可以获取相应的量级信息。除此之外,概念量级也可以用于传达模糊的量级信息(如量词,大量、少量)或量级范围和计量单位(如千克、毫克)等。
2.概念量级与数字的关系
概念量级与数字有着相似的心理表征,可以相互干扰。例如,在Gabay等(Gabay,Leibovich,Henik和Gronau,2013)的实验中,每个试次首先向被试呈现一个动物的图像作为概念量级,这些动物要么在概念上较小(猫或狗),要么较大(马或大象)。随后呈现一个数字,这些数字要么是较小的数值(2或3),要么是较大的数值(8或9)。结果发现,当概念量级大小和数字大小一致时,被试的反应时更短。另外,另一项研究发现概念量级与数字一样存在距离效应。Moyer和Landauer(1967)要求成年人比较两个阿拉伯数字,同时测量他们的反应时间。结果发现,反应时受到这两个数字之间的数字距离的影响,也就是说,反应时随着数字距离的减少而增加(例如,6和7的反应比2和7慢)。结果表明数字大小存在距离效应,即数字大小的差异越大,个体判断两者大小的速度就越快。在后续的一项研究中,Moyer(1973)向被试展示了成对的动物概念名称,要求被试选择较大的动物。与Moyer等人(1967)的结果类似,反应时与动物概念大小的差异呈显著负相关,概念大小差异越大,反应时越快。研究者认为在这个过程中被试将动物名称转换为动物实际大小的模拟表征后,通过"内部心理判断"来比较动物大小。而Dehaene和Cohen(1997)通过心理数字线来解释这种距离效应。研究者认为,将概念大小和数字大小转换成模拟量级,并把它们放在一个心理数字线上。随着心理数线上的表征逐渐接近,区分概念大小和数字大小逐渐变得更加困难。因此,当个体在加工概念量级和数字时存在着相似的加工机制。
二.空间数字联合反应编码(SNARC)效应
1.定义
空间数字联合编码效应(SNARC效应)是指:数值的大小分别与空间的左右联合。具体的,数字从小到大,依次从左到右排列。左边联系较小的数字,右边联系较大的数字。
Deheane等人(Deheane,Dupoux和Mehler,1990)进行的大小判断任务中,以65为参考刺激并对被试呈现一个数字作为测试刺激,要求被试判断该数字是大于65还是小于65。实验有两种实验条件,一种是当大于65时需要被试使用左手进行反应,而小于65时使用右手进行反应;另外一种是当小于65时使用左手反应,大于65时使用右手反应。实验结果表明,当呈现数字大于65时被试使用右手的反应时间要快于左手的;而当小于65时左手的反应快于右手的。Dehaene 将这种效应称为SNARC效应。
Dehane等人(Dehaene,Bossin和Giraux,1993)进行了对数字的奇偶性判断实验,实验会对被试呈现一个0-9的随机阿拉伯数字,并让被试判断该数字的奇偶性。实验有两种实验条件,一种是呈现奇数时需要被试使用左手进行反应,而呈现偶数时需要使用右手进行反应;另外一种是偶数使用左手反应,奇数使用右手反应。结果显示,无论是那种条件或者数字的奇偶性如何,被试的反应都有一种明显的倾向,即当出现相对较小的数字时(如1和2),被试使用左手的反应时间会少于使用右手的;当出现相对较大的数字时(如8和9),被试使用右手的反应时间会少于使用左手的。
2.发生阶段
根据信息加工理论,从刺激呈现到个体进行反应的过程中,感官可以分为三个主要阶段:刺激表征、反应选择、反应执行(Tombu,Asplund,Dux和Godwin等人,2011)。对于SNARC效应的发生阶段,研究者们主要提出了三种观点:(a)发生在刺激表征阶段;(b)发生在反应选择阶段;(c)既发生在刺激表征阶段,又发生在反应选择阶段。
(1)早期刺激表征阶段
一项研究支持了SNARC效应发生在刺激表征阶段。在同时诱发SNARC效应和Simon效应(14-2:个体、任务与环境)的研究中二者在反应时上不存在交互作用(引发一个效应对另外一个效应的反应时不会造成影响)。加因素法认为,如果两个过程发生在同一阶段,那么必然会相互影响导致认知资源竞争,在反应时上呈现出二者的交互作用;而如果二者发生在不同阶段相互独立,那么在反应时则不会受到影响(Liu,Park,Gu和Fan,2010)。经典的Simon效应在以往的研究中早已被确认为发生在反应选择阶段(Melara,Wang,Vu和Proctor,2008)。Tauka(2002)通过让目标数字随机出现在屏幕的左侧或者右侧并让被试做出相应的反应来同时诱发SNARC效应和Simon效应,发现被试的反应时并未表现出二者的交互作用,说明彼此独立,由此推断SNARC可能发生在早期的刺激表征阶段。
(2)晚期反应选择阶段
也有研究发现,同时诱发SNARC效应和Simon效应在反应时上存在交互作用(Gevers,Caessens,Fias,2005)。另外,Keus和Schwarz(2005)在数字奇偶判断任务中操纵了被试反应方式(左右按键反应/口头报告)时发现,SNARC效应只在被试以左右按键的方式反应时才被观察到。这些结果提示SNARC效应与左右空间反应方式有关,更可能发生在晚期的反应选择阶段。
(2)两阶段并存
当然,也有研究认为SNARC效应在两个阶段都有发生。Nan等人(Nan,Yan,Yang和Liu等人2021)在一个大小比较任务中同时引入发生在刺激表征阶段的Stroop效应(9-16:视觉特征整合)和发生在反应选择阶段的Simon效应,结果发现SNARC效应与Stroop效应和Simon效应都分别存在交互作用,支持了SNARC效应发生在两阶段的观点。
3.性质
(1)灵活性
SNARC效应具有灵活性,即可以根据任务需求进行动态调整。Dehane等人(Dehaene,Bossin和Giraux,1993)分别以0-5和4-9两个数值范围进行奇偶性判断任务。当数值范围是0-5时,4和5是相对较大的数字,实验发现被试右手的反应速度要快于左手的;当数值范围是4-9时,4和5是相对较少的数字,结果显示被试左手的反应要比右手的快。另外,Brysbaert(Brysbaert,1995)以11-90的随机数字作为刺激作相对大小判断任务(这些数字均比0-9大)。实验结果表明,当呈现相对较大的数字时(如90),右手比左手快;而呈现相对较小的数字时(如11,比9大),左手比右手快。
(2)方向性
SNARC效应不仅可以在水平方向上,还可以发生在垂直方向上。Lidji等人(Lidji,Kolinsky,Lochy和Morais,2007)使用钢琴和小提琴的音调为研究材料,音调分为高低两种,要求被试判断所呈现的音调是钢琴的还是小提琴的。这种任务设置可以让被试增加对乐器声音的注意,从而减少对音调高低的注意。实验结果显示,当呈现高音时,被试按上键的速度比按下键的快;而当呈现低音时,被试按下键的速度比按上键的快。
(3)非数字性和序列性
除了数字概念,在序列或一些可使用量表征的单位中也发现了SNARC效应。Fumarola等人(Fumarola,Da Pos和Umiltà,2014)以不同亮度的红色(或绿色)方块为材料,同时设置某一亮度为标准亮度。要求被试判断所呈现方块亮度比标准方块的亮还是暗,实验结果显示,当更暗时被试使用左手的反应时间要比右手的快,而当更亮时使用右手的反应时间要比左手的快。胡林成和熊哲宏(2011)以面积和亮度为研究材料,面积和亮度存在类似的SNARC效应。Rusconi等人(Rusconi,Kwan,Giordano,Umiltà和Butterworth,2006)在音调中发现了SNARC效应,研究结果显示,对于较高的音调,被试使用上键和右键的反应时间要比下键和左键的快;而对于较低的音调,使用下键和左键的反应时间要比上建和右键的快。
Gevers等人(Gevers,Reynvoet和Fias,2003;Gevers,Reynvoet和Fias,2004)使用用非数值(时间和字母)序列作为研究材料同样发现了SNARC效应。实验设置了两种实验任务,一是与序列相关的判断,需要被试判断所呈现的月份在7月之前还是7月之后;另外一种是与序列无关的任务,需要被试判断所呈现月份单词(荷兰语)的最后一个字母是否含有字母R。研究发现,不论是那种条件,被试对前面月份左手的反应时间要比右手的快,对后面月份右手的比左手的快。另外,当使用字母和星期作为序列刺激时,同样发现SNARC效应。
(4)影响因素
(a)后天环境和文化影响
Dehaene 等人(Dehaene,Bossin和Giraux,1993)认为,SNARC 效应受后天阅读和书写方向的影响。如Shaki和Fischer(2008)使用以从左到右书写的俄语文本和以从右到左书写的希伯来语文本作为实验材料。当读者在阅读俄语文本后发现了典型的SNARC效应;而在阅读希伯来语文本后发现了方向相反的SNARC效应(与典型SNARC效应方向相反。反向的SNARC效应具体表现为,当要求对小的数字反应时使用右手按按键的速度更快,而要求对大的数字反应时使用左手按按键的速度更快)。
(b)先天因素
Rosa Rogani进行了如下实验,她们在一个有五个小正方形的挡板后方放置了蜡虫,以此训练小鸡为了寻找食物走向挡板。经过训练后,将这个挡板撤走,换成两个带有相同数目的小正方形的挡板,分别置于左右两边,如图1。实验结果显示,当两个挡板的小正方形个数为2时,小鸡自发的走向左边挡板的概率超过70%。相反,当两个挡板的数量为8时。小鸡走向右边挡板的概率更高(资料来源:http://theconversation.com/like-most-humans- chicks-count-from-left-to-right-36736)。另外,其他研究在恒河侯(Rugani,Kelly,Szelest,Regolin和Vallortigara,2010)和7个月大的婴儿(de Hevia和Spelke,2010)中也发现了类似的效应。因此,这说明SNARC效应具有先天性。

图1
(c)加工深度
不同加工深度的SNARC效应具有一定差异,具体表现在SNARC效应的方向上。当被试需要注意到数字大小或奇偶性(具有概念意义的信息)时才能反应的加工属于深加工,如大小判断任务和奇偶判断任务。当被试只需对物理属性作反应的加工属于浅加工,如颜色判断和方向判断。一些研究发现,当进行浅加工时SNARC效应仅在水平方向上被激活(沈模卫,田瑛和丁海杰,2006)。而当进行深加工时,水平和垂直方向的SNARC效应都被激活(Müller和Schwarz,2007)。
(d)心理表象
Bächtold等人(Bächtold,Baumüller和Brugger,1998)要求被试把数字想象成钟表上的时刻,并随机呈现一个1-11(除去6)的数字。被试需要做的是判断该数所代表的时间是早于6点还是晚于6点。研究发现,当呈现数字为1-5时,被试右手的反应速度要快于左手的;而当呈现数字为7-11时,被试左手的反应速度要快于右手的。该实验结果表现出了反向的SNARC效应。研究者认为,这是由于在钟表上1-5位于6的右侧,而7-11位于6的左侧,被试关于钟表的表象影响了SNARC效应的方向。
4.机制
(1)心理数字线
人们在对数字表征时会自动地将小数与左侧空间联系,同时将大数与右侧空间联系,就好像在大脑中存在一条按数字大小从左到右排列而成的数字线一样,或者说,在心理上存在着一条按照数值大小依次从左到右排列的数字线。研究者将这条数字线称为心理数字线(Berch,Foley,Hill和Ryan,1999),这为数字和空间的心理连接关系提供了依据。
例如,一个实验(Hubbard,Piazza,Pinel和Dehaene ,2005;Calabria和Rossetti,2005)要求被试对一系列由红色"X"组成的线段进行对分时,被试能够准确的从线段中点将其平分;而当线段的组成部分由"X"改为英文数字单词"two"时,被试给出的中分点会偏向线段中点的左侧,当线段组成由"X"改为"nine"时,被试给出的中分点会偏向线段中点的右侧,实验结果表明尽管数字大小和任务要求无关,但是数字与心理数字线上的空间位置的连结效应还是被自动激活,引起空间注意的偏转,从而造成错误判断。
(2)隐喻构念观
一些研究者认为SNARC效应的方向受到被试的阅读方向和书写方向影响,比如一项研究发现SNARC效应随着伊朗被试(阅读习惯是从右到左)移民到法国(阅读习惯是从左到右)的时间的长短发生线性变化。而在一项发展性研究中发现,美国儿童直到四年级才在任务中显示出SNARC效应。虽然三年级的儿童也能很好的完成奇偶判断,但没有显示出映射SNARC趋势。因此,SNARC效应可能是随时间慢慢习得的,并且受阅读经验影响。这一事实意味着数字和空间的映射关系可能是一种文化产品。(Dehaene,Bossini和Giraux,1993)
(3)极性编码理论
极性对应理论(Proctor和Cho,2006)认为,数字和空间的联结是由于刺激和反应的极性重叠而导致的。刺激和空间可以呈现为正极或负极,如小-大、奇-偶、左-右、上-下...中,每一维度的一端对应一极。在SNARC效应中,在水平方向上,"左"属于负极性,"右"属于正极性。在垂直方向上,"上"属于正极性,"下"属于负极性。当刺激和反应的极性一致时被试反应要比极性不一致时的快。因为数字的"大"属于正极性,所以"大"与"右"或"上"联系时要比和"左"和"下"联系的快。同理,"小"是负极性,所以它与"左"和"下"联系时要比"右"和"上"的快。
(4)双路线理论模型
双路线理论模型(Gevers,Caessens和Fias,2005)认为,存在一条预先以编码好的"刺激-反应"自动通路,又被称为快速无条件通路(Unconditional Route);同时存在一条根据任务需求而定的通路,被称为慢速条件通路(Conditional Route)。当刺激出现时,两条通路会被同时激活。在SNARC效应中,在快速无条件通路中,小数预设为与左侧空间联结,大数与右侧空间联结;在慢速条件通路中,被试需要根据任务要求而定(如根据要求对大数按左键或右键)。当呈现大数时,在快速通路会激活右侧空间(以预设),如果要求被试对大数按右键,则慢速通路和快速通路相容(都是右侧),反应时间会更快;反之,如果要求被试对大数按左键,则慢速通路和快速通路冲突(一个右侧,一个左侧),从而导致反应变慢。
(5)双重编码理论
人们在对物体编码时会同时运用两种不同的表征系统,一种是表象系统,人们在脑海中可以用"图象符号"来直观的反映物体;另一种是语义系统,人们可以用"文字符号"来代表物体。数字在空间上的编码也可以同样使用这两种编码系统,极性对应理论认为概念"小"和"左"涉及相同的负极("-"),而概念"大"和"右"涉及相同的正极("+"),因此SNARC效应是由语义系统产生的;而双路线理论模型认为,SNARC效应的产生是由于数量标记(小-大)与空间表征标记(左-右)之间存在习得性联结,因此这种效应是由表象系统产生的。Gevers等人(Gevers,Santens和Dhooge和Chen等人,2010)在极性对应理论和双路线理论模型的基础上提出了言语空间编码说,该理论认为SNARC效应并不仅仅是由内部的心理数字线表征(表象系统)造成,也是由数字跟言语概念(如小、大和左、右)的联结造成(语义系统)。
(6)工作记忆理论
Van Dijck等人(van Dijck和Fias,2011;van Dijck,Abrahamse EL,Majerus和Fias,2013)在研究中给被试先后呈现一串数字(如逐个呈现9、1、7、2),然后呈现一个目标数字并要求被试对其进行奇偶性判断。实验发现,当目标数字处于被试所记住的随机数字串时,SNARC效应并未出现(即左手并未对小数反应更快,右手也未对大数反应更快),且如果该目标数字位于数字串的开端(如9)时,被试的左手反应比右手的快;而目标数字位于数字串的末端(如2)时,被试的右手反应比左手的快。这种现象被称为序列位置效应,该效应同时在数字序列和非数字序列中发现。因此研究者提出,被试将被存储于工作记忆的序列编码为一个任务集,如果目标刺激为序列中较早出现的项目,则与左侧关联,如果目标刺激为序列中较晚出现的项目,则与右侧关联。自然数中,较小的数一般为处于序列的早期,较大的数一般处于序列的晚期(如1先于2,2先于3...)。因此小的数总与左侧关联,大的数总与右侧关联,表现为SNARC效应。
(7)量级理论(ATOM)
Walsh(2003)在总结了前人的一系列理论后,提出了量级理论。该理论认为时间、空间和数量的信息加工可能共享同一个量级加工系统。个体将不同维度(时间、空间和数量)的信息进行加工,形成同一形式的量级表征,即心理数量。Walsh认为该量级系统位于顶叶皮层,尤其是沿着右后顶叶皮质(PPC)的右侧顶底沟。在心理学上,以发现了SNARC效应(空间和数量的关联),另外还有TNARC效应(时间和数量的关联)和STEARC效应(空间和时间的关联)(9-5:时间)。
5.心理数字线与心理时间线的比较
数字作为与时间类似的抽象概念,在心理表征上与时间也具有很多相似之处,比如左右、前后、上下三个维度都发现了SNARC效应。更重要的是,在起源上两者也有类似之处。比如左右维度的心理数字线也起源于阅读/书写习惯。阅读书写习惯从左至右的个体(英语、汉语等被试),其心理数字线的方向也是从左至右的;相反阅读书写习惯从右至左的个体(阿拉伯语和希伯来语被试),其心理数字线的方向则是从右到左(Fuhrman和Boroditsky,2010)。在上下维度上,其可能的起源之一是空间隐喻。我们在语言表达上经常会说"高分"、"低分"、"高智商"、"低智商"。其次也可能起源于日常生活经验。由于重力作用,我们常常知觉到"多即是上",比如倒水或者放东西的时候都是数量越多,高度越高。最后,也有研究发现心理时间线和心理数字线并非完全一致(Pitt,Scales和Casasanto,2018)。(何听雨,丁一,李昊堃和程晓荣等人,2020)
三.时间数字的联合反应编码(TNARC)效应
数量加工和时间加工之间存在一定的交互作用,数量大小会影响时间加工,这种影响通常表现为大数量导致时间高估,小数量导致时间低估。因此如SNARC效应一样,在时间和数字中同样存在类似效应,即TNARC效应。这个现象中数量表现的形式多种多样,例如刺激的数字大小、物理大小、刺激个数的多少、刺激强度的大小、速度的大小、距离的长短甚至一个表情动作跨度的大小都会影响到知觉到的时间,数量大的刺激与长时间联结,数量小的刺激与短时间联结(靖国民,2016)。
1.研究内容
在一个时间估计任务中,要求被试判断测试刺激(给出其中一个数字1、5和9)的持续时间(250ms-350ms,间隔10ms)比事先给定的一个标准刺激的持续时间(数字5,持续时间为300m)长还是短。结果显示,数字影响了时间的加工,被试倾向于低估小数字(如 1)的持续时间,高估大数字(如9)的持续时间。在进一步的实验中将数字换成两位数的阿拉伯数字(11、15、19),结果发现数字对时间知觉的影响在两位数中同样存在,大数字(19)引起了持续时间的高估,小数字(11)引起了持续时间的低估,因此,这表明这种效应中数字大小的表征是相对大小。(Oliveri,Vicario,Salerno和Koch等人,2008)
Xuan等人(Xuan,Zhang,He和Chen,2007)用先后呈现的三个数字把一段时间间隔成两部分,让被试比较两段时间间隔的长短,结果发现,相比数字差的大小与时间间隔不一致(数字差比较大,时间间隔却比较短;或数字差比较小,时间间隔却比较长),当数字的差的大小与时间间隔的长短一致时(数字差比较大,间隔时间比较长;或数字差比较小,时间间隔比较短)被试的正确率更高。
Kiesel和Vierck(2009)探讨了数字大小与反应持续时间大小的关系。实验采用奇偶判断任务,要求被试用"滴"反应对奇数作出反应,用"哒"反应对偶数作出反应。其中"滴"反应是短持续时间的按键(按键的持续时间不超过150毫秒),"哒"反应是长持续时间的按键(从151毫秒到300毫秒),如果时间与数字之间存在联系,那么在反应阶段对时间的操纵应该会影响数字的处理。结果发现,数字的大小和反应时间长短之间存在关联,当大数字对应长时间按键,小数字对应短时间按键时,反应时更短,正确率更高。
如在实验中给被试呈现两个刺激(如两个不等的数字,两组不同数量的点集等),并且两个刺激呈现的时长不一样。然后让被试判断两个刺激中哪一个刺激的呈现时间更长或更短。实验证明,被试会倾向于认为较大刺激(数字更大、点数更多)的呈现时间更长,而认为较小刺激的呈现时间更短。(Hurewitz,Gelman,Schnitzer,2006;Kiesel和Vierck,2009;Xuan,Zhang,He和Chen,2007)
2.数字影响时间知觉的发生阶段
在时间知觉的任务中,人们通常是先对知觉到的时间进行编码(编码阶段),然后把时间编码放进记忆(记忆阶段),再去知觉下一段时间,并与记忆中的时间段比较然后做出决策,如图2。在数字对时间信息加工产生影响的过程中,这种影响究竟发生在哪个阶段呢?
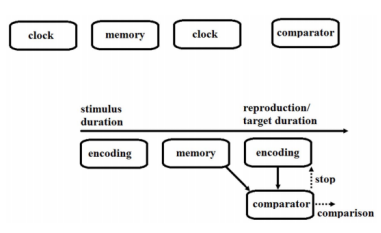
图2
Chang(Chang,Tzeng,Hung和Wu,2011)使用时间复制任务对此问题进行了研究。在该任务的时间感知阶段,先给被试呈现一个数字(1,2,8和9);时间呈现结束后有一个1000ms的空屏间隔,在此过程被试需要保持对数字呈现时间(300ms,450ms,600ms,750ms)的记忆;之后,在时间复制阶段,要求被试持续按0键复制呈现数字的持续时间。结果发现被试复制出大数字(8和9)的呈现时间显著大于小数字(1和2)的,出现了TNARC效应,在后继的实验中,先给被试呈现一个绿点(300ms,450ms,600ms,750ms),随后是一个1000ms的空屏时间,接着要求被试按0键复制绿点的呈现时间,被试在按下0键后屏幕上出现数字(1,2,8和9),发现大数字导致复制的时间变短,小数字导致复制的时间变长。上述结果说明数字对时间加工的影响发生在时间的编码阶段。
上述实验存在有一个问题,由于时间感知阶段和时间复制阶段之间有一个空屏时间,因此在第二个实验中时间复制阶段呈现数字影响的是保持在记忆中的绿点呈现时间,即数字影响的是记忆阶段中保持的时间而非编码阶段的。为了验证这个问题,Cai和Wang(2014)在他们的研究中重复了Chang et al.(Chang,Tzeng,Hung和Wu,2011)的实验却发现了不同的结果。唯一不同之处在于时间感知阶段和时间复制阶段之间没有空屏时间。结果在Cai和Wang的研究中,当数字出现在时间复制任务的时间感知阶段时,复制出的时间受到数字的影响,大数字被认为时间更长小数字被认为时间更短。但是当数字出现在时间复制阶段时,数字大小对复制出的时间并无影响。这与 Chang等人的研究结果不同,由此,Cai和Wang等人推断数字对时间加工的影响不是发生在编码阶段而是发生在记忆阶段。
3.空间注意的作用
在Fischer等人(Fischer,Castel,Dodd和Pratt,2003)的研究中,首先在屏幕中央呈现一个阿拉伯数字,然后再呈现目标刺激,让被试对目标刺激作出反应而无视之前的数字。结果发现,若先呈现的是小数字(1或2),则目标刺激出现在左侧视野时被试反应较快;若先呈现的是大数字(8和9),则目标刺激出现在右侧视野时被试反应较快。这表明即便数字为无关刺激时,数字也能对空间注意产生影响,因而造成注意在水平方向上发生转移,对小数字进行加工会导致空间注意向左侧视野转移,对大数字进行加工时会导致空间注意向右侧视野转移。
Frassinetti,Magnani和Oliveri(2009)在其研究中使用一种棱镜适应的方法,操纵被试的注意力向左或向右,然后让被试完成时间复制任务,发现了当注意力向右引导时,被试高估了时间段,向左时低估了时间段。而Vicario等人(Vicario,Caltagirone和Oliveri,2007)也发现当注意力向右时被试倾向于高估时间,当注意力向左时,被试倾向于低估时间。但这个现象只出现在秒级以下的时间任务中,秒级以上的时间任务中这个现象消失。
综合以上关于数字与空间注意、空间注意与时间信息加工的相关研究,研究者们推断,时间加工中数字和时间之间的联结可能是由于数字的出现导致空间注意的转移,大数字导致注意力向右转移继而导致时间的高估,小数字导致注意力向左转移继而导致时间的低估(Oliveri,Vicario,Salerno和Koch,2008)。
4.概念量级与时间
Bottini等人(2010)在探究内隐空间长度对时间知觉的影响时,向被试展示了一些比如"香烟"、"长凳"以及"高速公路"等在现实中代表不同长度物体的概念符号。结果发现,表示更长物体的概念符号导致主观持续时间更长、表示更短物体的概念符号导致主观持续时间更短。张嘉欣(2021)使用长度计量单位("千米"和"毫米"),探究这类概念量级是否会影响时间知觉,实验使用时间复制任务要求被试通过持续按键的方式复制该概念量级的呈现时长。结果发现,当呈现的刺激材料为大概念量级(千米)时,被试的复制时长显著长于小念量级(毫米)的。因此,以上研究表明,概念量级可以对时间知觉产生影响。
5.相对性
相对数量效应认为,决定是否影响时间知觉的,是相对数字大小而不是绝对数字大小(黄倩,程晓荣和定险峰,2015)。有研究者提出时间判断会受到刺激所呈现的背景的影响,也会受到前一次试次中呈现的刺激以及实验中同时呈现的其他刺激的分布。例如,Matthews等人(Matthews,Wearden和Stewart,2011)探究刺激强度与主观持续时间的关系是取决于刺激的绝对强度大小,还是取决于刺激与背景之间的相对强度差异。在实验验中浅灰色或深灰色的正方形作为测试刺激。同时,参与者还需在两种背景条件下完成任务,一种是在白色背景,另一种是在黑色背景。研究者认为如果绝对强度决定了主观时间,那么无论背景如何,浅灰色的正方形(亮度更高)的主观持续时间应该更长;如果刺激与背景的差异更重要,那么浅灰色的正方形在黑色的背景下的主观持续时间应该更长,而在白色的背景下的主观持续时间应该更短。研究结果显示,刺激亮度对持续时间判断的影响取决于背景。在黑色的背景下,浅灰色正方形的主观持续时间要比深灰色正方形的更长。而在白色背景下,深灰色正方形的主观持续时间要比浅灰色正方形的更长。另外,研究者还使用了声音强度作为刺激进一步地验证了此结论,在高强度背景下,安静声音的主观持续时间要比响亮声音的更长。因此,研究者认为刺激的相对强度而不是绝对强度是判断持续时间的主要决定因素。Linares和Gorea(2015)也发现了在移动的环境下呈现移动的刺激,时间判断更取决于刺激与环境之间的相对速度而不是绝对速度。
四.数量表征系统
1.近似数表征系统(ANS)
人们天生就有对非符号数量进行估计的能力,即将场景客体的实际数量映射为心理数量。如估计场景中的客体数量:"树上大概有多少个苹果?树上有60个苹果(客体数量),但估计者估计为50个或者55个(心理数量)"。这种估计并不是毫无规律的,而是遵循梯度变异性或者韦伯定律的,即心理数量与实际数量的对数值成正比(Brannon,2006)。韦伯定律有两个特点,距离效应和大小效应(又称比率效应)。距离效应是指两个数距离越大时,区分它们越容易,反应时间越短;反之则越难区分,反应时间也越长(Moyer和Landauer,1967)。比如比较5和9的大小,其反应时间会比比较5和7的快。大小效应是指距离相等的两组数字(如1和9,91和99,这两组数字的距离都为8),数字越小区分它们越容易,反应时间也越短(Buckley 和Gillman,1974)。如比较1和9大小的反应时间,会比比较91和99的快。
心理数量与实际客体数量之间的对数关系是一种理想模型,它们之间实际上还存在着高斯分布的噪音。也正是这些噪声给估计带来不确定性(不然,给定一个实际客体数量,就可明确其心理数量,而非一个估计值)。 因此从韦伯定律加上噪声可进一步得到线性模型(图3(a))和对数模型(图(b))(Feigenson,Dehaene,Spelke,2004)。线性模型和对数模型都是对添加了噪声的韦伯定律的解释,但其解释方式不同。线性模型认为实际数量与心理数量呈线性关系(即简单理解为y=ax,y为心理数量,x为实际数量,a为常数)。但当实际数量越大时,噪声的方差就越大,心理数量之间的高斯区间重叠程度就越大,不确定性就越大,因而最终表现为对数关系。对数模型认为噪声的方差对于所有实际数量都是一样的,而实际数量与心理数量是对数关系(类比为y=lnx,ln为对数函数),因而呈现对数关系。
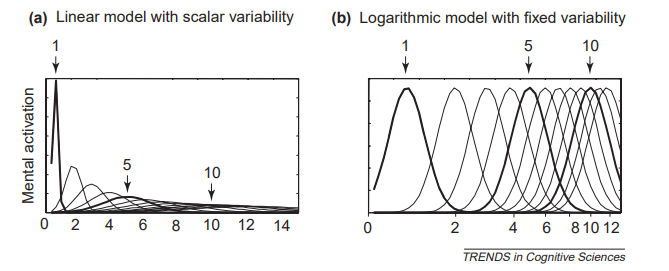
图3
2.精确数表征系统(ENS)
近似数表征系统能对数进行估计,但它并不能满足数学和精确计算的要求。因此还存在一种称为精确数表征的系统。在近似数表征系统中,心理数量与实际数量呈对数关系。而在精确数表征系统中,实际数量与心理数量之间是线性关系。
3.其他表征
(1)负数
正数是一系列从小到大、从左至右排列在心理数字线上的数。而关于负数心理表征的理论有两种,系统进化论和个体发展论。系统进化论认为,心理数字线只能模拟正数表征,而不能模拟负数。系统进化论对应的加工策略是部分加工模型。当需要模拟负数时,需要将负数的符号部分和数字部分分开加工(如"-9"可分为符号"-"和数字"9"),并只有数字部分(即9)置于心理数字线上。有研究(Ganor-Stern和Tzelgov,2008)采用两个负数的大小判断任务(如判断-10和-19的大小)时,出现了反向的SNARC效应。之所以会出现这种现象,系统进化论认为因为只有负数的数字部分能表征在心理数字线上,而更小的负数(-19)的数字部分(19)比更大的负数(-10)的数字部分(10)大。因此,更小的负数实际上处于心理数字线更右侧的位置,而更大的负数处于心理数字线更左侧的位置,从而导致反向SNARC效应。
个体发展论认为负数是心理数字线上的一部分,负数在心理数字线的左侧,而正数在心理数字线的右侧。个体发展论对应的加工策略是整体加工模型,即将负数的符号和数字一起置于心理数字线进行加工(简单点说就是正数和负数都在心理数字线上加工)。Shaki和Petrusic(2005)使用大小相差1的负数对(如-3和-4)进行大小判断任务,结果出现了正常的SNARC效应。
(2)序数
序数是指有序列结构和顺序意义的数,顺序意义是对于一个系统而言的,如一周(系统)里的星期几和字母表(系统)中的字母。数的顺序意义包括自然数的顺序、每个数在自然数数列中的位置和数与数之间的关系(Fuson,1988)。一项研究发现(Terrace,Son L和Brannon,2003),恒河猴能够学习一个包含7个刺激的序列,该序列并非时间上的先后关系,而是第一、第二等数字类别概念。另外,其他相关研究表明(Fuson,1988;Wynn,1992),3岁大的幼儿能够从1数到10,但他们分不清7和9哪个大,因此他们并不知道数字的含义。这表明序列的顺序和数量可能存在两套表征机制。
Turconi 等人(Turconi,Campbell和Seron,2006)在实验中给被试呈现一些数字对(如2与5),并要求被试比较这两个数字的大小或者判断两个数字的序列关系(如回答2与5是升序还是降序)。结果发现不论被试进行的是比较大小任务还是判断顺序任务,都出现了距离效应。但在进行比较大小任务时,升序数字对(如2与5)的距离效应不如在降序数字对(如5与2)的那么明显。这说明,距离效应与数字的顺序存在交互作用。
(3)分数
分数在我们的日常生活中无处不在,如"一口气喝了半瓶汽水"、"给我1/4个苹果"。很多研究表明,人类和一些动物能够表征两个非符号数量之间的比例关系,而且这样的比例表征是基于近似数量表征的。如恒河猴在看到两条长短不同的目标线段对后,可以在备选项中选出长短比例与目标线段对一致的线段对, 且所选出的线段对和目标线段对的绝对长度并不一样(Vallentin和Nieder,2008)。6个月的婴儿在观察由一定数量的蓝色点子和4倍数量的黄色点子组成的刺激后(即蓝色点和黄色点的比例为1:4),他们注视含有新数量比例图片(如 1∶2)的时间比原有比例(1∶4)的时间更长(婴儿在观察不熟悉的或者新异的刺激时,注视时间会更长)。另外,这些婴儿能区分1:4和1:2 的刺激(两个比例相差 2 倍),但不能区1:3和1:2的刺激(两个比例相差 1.5 倍)。因此,婴儿对数量比例的区分受它们之间的数量距离差异调控,表明他们可能是使用近似数量表征在表征数量比例(McCrink和Wynn,2007)(近似数表征的是整数,因此1.5倍无法识别)。但也有其他一些研究认为非符号比例表征并不基于近似数表征系统,而是利用另一种专门用以表征及加工比例信息的比例加工系统(Matthews和Chesney,2015)。
五.形式与表征
许多研究表明,非符号数量是通过近似数表征系统进行表征的(Reynvoet,Sasanguie,2016)。但对符号数量的表征系统仍然存在争议。
1.近似数表征系统与符号数
近似数表征系统作为人与动物共有的先天的数量表征系统,可以对非符号数量进行表征。然而随着人类文明的发展,符号数量在人类社会中扮演着越来越重要的角色。那是否有一种可能,符号数量是从近似数表征系统中发展起来的呢?Siegler和Braithwaite(2017)提出的近似符号映射理论认为,符号数量通过映射到近似数表征系统的某个数值位置来获得相应的数量含义。简单点说,符号数量的表征是基于近似数表征系统的。
距离效应和大小效应是近似数表征系统的两个重要特点。因此,如果符号数量也同样存在距离效应与大小效应,那么就能证明符号数量使用的是近似数表征系统。大量研究表明,符号数量具有与非符号数量相似的距离效应和大小效应(Holloway和Ansari,2009)。
2.精确数表征系统与符号数
也有研究认为,符号数量并非通过近似数量系统表征的,而是通过另一个更准确的精确数表征系统。Núñez(2017)认为,与滑雪板一样,符号数字未必是一种先天能力,而可能是通过后天训练而掌握的。尤其是语言,它在精确数习得中具有重要作用。目前,证明符号数量不使用近似数表征系统进行表征的方式有两种:一是,虽然符号数也有非符号数的距离效应和大小效应,但是它们的这两种效应并不相同。如在一项研究中发现,符号数的距离效应比非符号的小(Holloway和Ansari,2009)。二是,有研究发现符号数量在任务中表现为线性表征而非对数表征。如Marinova等人(Marinova,Sasanguie和Reynvoet,2019)的研究中发现,符号数量在比较任务(如比较91和99的大小)中没有发现大小效应(显然,线性关系有距离效应,但无大小效应;而对数表征则需同时存在这两种效应)。
Krajcsi等人(Krajcsi,Lengyel和Kojouharova,2018;Krajcsi,Lengyel和Kojouharova,2016)认为,符号数量是通过具有语义的结点进行表征的,不同节点表示不同符号数量(如表征"3"的节点表征数字"3",表征"10"的节点表征数字"10"),节点之间的关系反应了符号数量之间的关系。该理论还认为,由于小数出现频率高并且更熟悉,因此也会产生大小效应(与Marinova等人(Marinova,Sasanguie和Reynvoet,2019)的研究结果相矛盾)。Carey(2001)认为人们在学习过程中掌握了符号数字的关键原理,如"顺序"(数字构成序列,如1、2、3...)和"序列功能"(如3的前一个数字是2)。之后,通过将这些原理逐步应用到更大的符号数字,从而对符号数字系统有了完整了解。总结来说,符号数字通过语义节点进行表征,并且各数字符号通过如顺序和序列等关系进行关联。
3.两个表征系统对符号数的共同表征
还有一些研究认为,符号数字是通过近似数表征系统和精确数系统共同表征的。Anobile等人(Anobile,Cicchini和Burr,2012)采用双任务范式(颜色判断任务和符号数量判断任务)研究了注意在符号数字表征中的作用,当只进行单任务时(只判断数量),被试的数字判断表现出线性性,即表现出精确数表征系统的特征;而在进行双任务时,数字判断呈现出对数性,即表现为近似数表征系统的特征。
六.数学能力
人类拥有强大的数学能力。但是绝大部分数学能力并非由于进化获得的,比如人类不可能进化出专门用于处理复变函数或泛函分析的脑区。这些复杂的数学是通过语言和逻辑推理得到的。为了探究人类先天的数学能力,可以从动物或还没发展出语言能力的婴儿中发现。
Carey和Xu(2001)使用违背预期范式对婴儿的简单加减法进行研究。在该类实验中,研究者把一个玩具放在婴儿看得见的地方,然后对玩具进行遮挡使婴儿无法看见,因为物体恒常性的原因(虽然婴儿已经看不见,但婴儿知道一个物体不会凭空消失),婴儿知道遮挡处的背后有一玩具。接着,研究者当着婴儿的脸在遮挡处背后再放一个玩具。然后,研究人员将遮挡物拿走,婴儿可能会看到两种情况,一种是只有一个玩具(因为有一个玩具已经被研究人员偷偷拿走,但婴儿看不到这个过程),另外一种是有两个玩具。如果婴儿具有加法能力,那么他应该能预知遮挡处背后有两个玩具。因此,比起看到两个玩具的情况,看到只有一个玩具时婴儿应该感到更加惊讶从而注视时间更长。实验结果显示,婴儿不但能判断"1+1=2",还能判断"2-1=1"。
目前关于非语言的数量表征模型包括上述的模拟量模型和客体档案模型。模拟量模型认为,一个刺激就是一个神经冲动,该神经冲动会在累计器中被累积。当两个刺激先后出现时,便能使累计器产生"2"的激活量(这个"2"只是为了说明使用)。因为客体数量在记忆中的数量感的波动和变化,所以从累加器中输出的是一个近似值,输出量的增长幅度与记忆中的量成比例。(Cordes,Gelman和Gallistel,1983)。客体档案模型认为,如果已经有一个或者几个客体文档被打开,如果再打一个新文件就是一个加法过程,且文档的最大打开数约为4个(Carey和Spelke,2001)。
模拟量模型和客体档案模型处理的情况是不同的。客体档案模型倾向于处理小数量的情况。在一项研究中(Feigenson,Carey和Hauser,2002),有两个箱子分别放有不同数量的饼干,当两个箱子的饼干数量分别为1和2,或者2和3时,10个月大的婴儿能爬向数量多的。而当饼干数量分别为3和4、2和4、3和6时,因为1和2、2和4、3和6有同样的比例,如果婴儿的判断是依靠比例而非实际数量,那么这3种情况下(1和2、2和4、3和6)婴儿应该都会走向饼干数量多的箱子。而结果显示,婴儿的选择是随机的,他们无法判断哪个箱子更多饼干。因此,该研究支撑了客体档案模型,即不是处理比例,也无法处理4及以上的数。模拟量模型倾向于处理大数量的情况,有研究表明(Xu和Spelke,2000),婴儿能够区分8和16的点数。这时所呈现的数量已远远超出客体档案数的最大范围,所以无法使用客体档案理论解释,而只能使用模拟量模型解释。
七.量级感知-费希纳定理
德国物理学家心理学家Fechner从韦伯定律的基础出发,进一步的得出了费希纳定理。这条定理表明,物理量与心理量之间是一种对数关系,其公式为S=KlgR,其中S是感觉强度,R是刺激强度(物理量),K是常数,lg是底为10的对数函数。正如噪声的心理强度使用分贝来衡量,当声音的物理振幅增大十倍时,人所感受的音量仅增加一分贝。对其他物理量的感受,如触觉、味觉、嗅觉、电击觉、温度觉和重量均符合该规律。经济学的边际报酬递减律表明,效用与收益之间的关系也符合费希纳定理。其他心理量,如情绪、情感等,都符合费希纳定理。这说明无论是物理上的还是心理上的,比起绝对量,人们更容易感知大小的相对变化,或者说,更容易察觉大小的相对变化。如同样是变化10,当量值为1时大小的相对变化为10倍,而量值为10时,大小的相对变化只有1。
常数K是由最小可察觉量△R与当前的刺激量R的比值确定的,K=△R/R。而最小可察觉量是指刚刚能引起差别感觉的最小刺激变化量。我们都有这样的体验,当我们手上什么都没有时,仅拿起0.1kg的物体我们很容易就察觉。但当我们手里拿着10kg的物体时,此时只加0.1kg我们却很难发现。根据最小可察觉量△R=K*R,并假设K=0.1。当我们手拿10kg的东西时,如果要使我们感觉到手上的重量有变化,那么最少增加的重量为0.1*10kg=1kg。因为0.1kg少于1kg,增加0.1kg不能使我们感觉到变化。而当手上没有东西的时候,最少增加的重量为0.1*0kg=0kg,因此此时无论增加多少重量,我们都能察觉到变化。