朱启等
1深圳大学计算机与软件学院,中国深圳
2宁波诺丁汉大学计算机科学学院,中国宁波
3深圳大学人工智能学院,中国深圳
https://arxiv.org/pdf/2601.21541
摘要
注意力机制因其建模长程依赖的能力,已成为现代视觉骨干网络中的关键模块。然而,其计算复杂度随序列长度呈二次方增长,且注意力权重难以解释,限制了模型的可扩展性与清晰度。近期的无注意力架构表明,无需成对注意力亦可实现优异性能,这推动了对替代方案的探索。本文提出Vision KAN(ViK),一种受科尔莫戈罗夫-阿诺德网络(Kolmogorov-Arnold Networks)启发的无注意力骨干网络。其核心为MultiPatch-RBFKAN,一种统一的令牌混合器,融合了:(a) 基于径向基函数(RBF)的KAN进行块级非线性变换,(b) 轴向可分离混合以实现高效局部传播,© 低秩全局映射以建模长程交互。该设计将KAN作为注意力模块的即插即用替代方案,通过采用块级分组策略并结合轻量级算子恢复跨块依赖,解决了全量KAN在高分辨率特征上计算成本过高的问题。ImageNet-1K上的实验表明,ViK以线性复杂度实现了具有竞争力的准确率,验证了基于KAN的令牌混合可作为高效且理论基础坚实的注意力替代方案。代码:https://github.com/SeriYann/ViK
关键词---科尔莫戈罗夫-阿诺德网络,无注意力视觉骨干网络,令牌混合
1. 引言
近年来,视觉骨干网络主要由基于注意力的架构主导。Vision Transformer(ViT)[1]证明,将图像建模为图像块序列并通过自注意力处理,其性能可媲美甚至超越卷积网络,从而确立了注意力作为通用视觉建模工具的地位。后续变体进一步拓展了这一方向,如Data-efficient Image Transformer(DeiT)[2]提升了训练效率与实用性,Pyramid Vision Transformer(PVT)[3]通过空间缩减引入层次化特征图,将Transformer与多尺度表征相连接。
尽管取得成功,注意力模块面临两大局限:首先,其计算与内存复杂度随令牌数量呈二次方增长,使其难以扩展至高分辨率图像[4];其次,自注意力中的令牌间亲和力矩阵与语义或结构线索无直接关联,限制了可解释性[5]。这些局限推动了无注意力骨干网络的发展------这类网络保留Transformer架构,但以替代性令牌混合器取代注意力。MLP-Mixer[6]证明通道与令牌MLP可实现竞争性性能,而MetaFormer[7]进一步表明,由归一化、令牌混合器和通道MLP组成的骨干支架即使不含注意力机制亦可有效。这些工作共同表明,视觉任务的优异性能本质上并不依赖二次方注意力,这激励我们探索基于函数的、有原则且高效的替代方案。
与此同时,科尔莫戈罗夫-阿诺德表示定理(K-A定理)[8]提供了强大的理论洞见:任意多元连续函数均可表示为一元函数的组合,即 f(x1,...,xn)=∑qϕq(∑pϕpq(xp))f(x_{1},\ldots,x_{n}) = \sum_{q}\phi_{q}\Bigl(\sum_{p}\phi_{pq}(x_{p})\Bigr)f(x1,...,xn)=∑qϕq(∑pϕpq(xp)),其中 ϕ(⋅)\phi(\cdot)ϕ(⋅) 为连续一元函数。这为建模令牌交互提供了基于函数的视角,区别于成对相似性或线性投影。Kolmogorov-Arnold Networks(KANs)[9,10]及其在多领域应用[11,12,13]的最新进展已展现出强大的函数逼近能力、局部可解释性与跨域适应性,为设计新型骨干模块指明了方向。
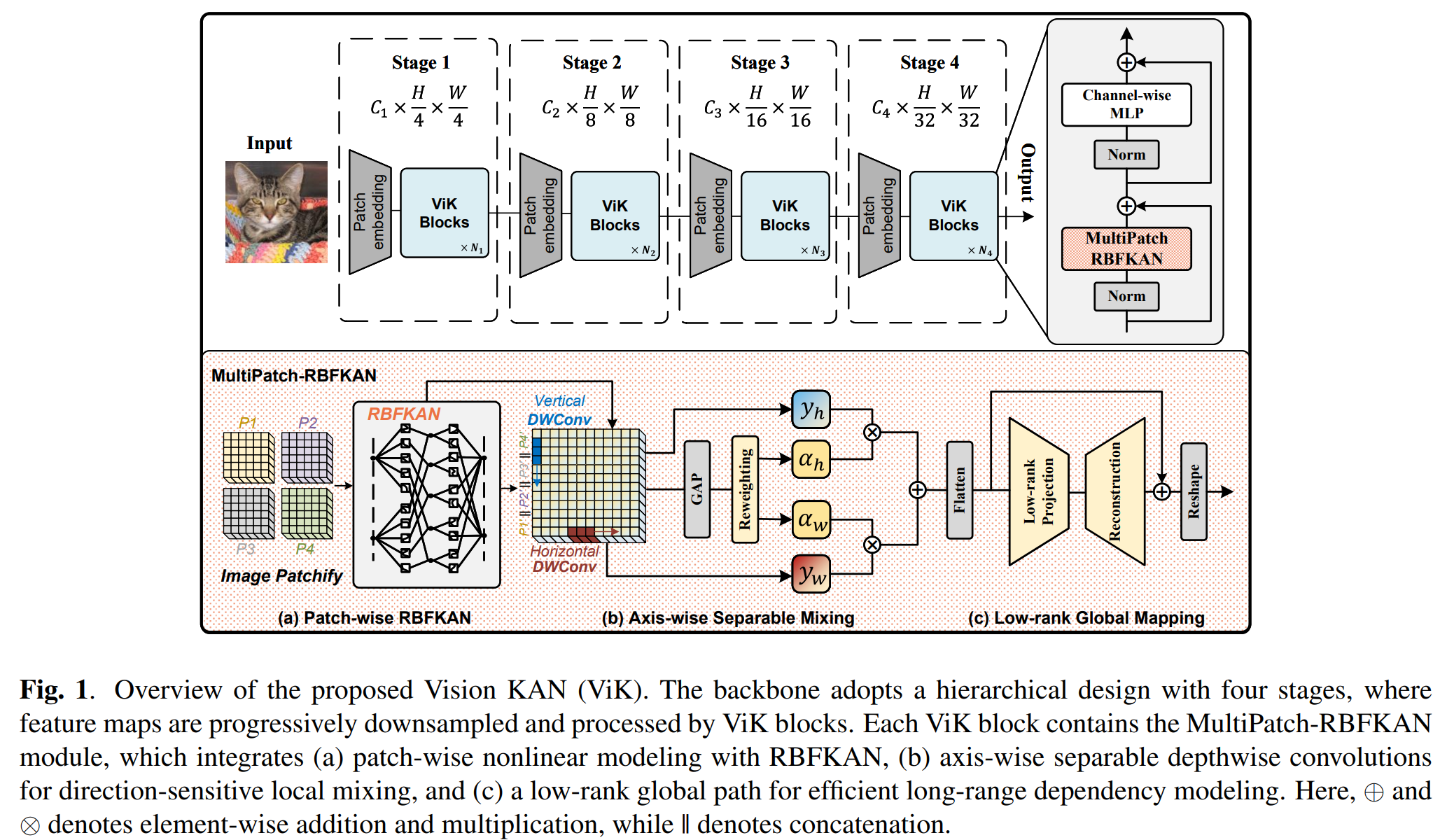
基于上述洞见,我们提出Vision KAN(ViK),一种无注意力视觉骨干网络,以受K-A定理启发的基于函数的令牌混合器替代成对注意力。核心组件为MultiPatch-RBFKAN,它融合了基于RBF的块级非线性建模、轴向可分离混合与低秩全局映射。关键挑战在于:直接对高分辨率特征应用全量KAN层计算成本过高。因此,我们采用块级分组策略使KAN可规模化应用。为补偿分组引入的跨块交互受限问题,可分离混合增强局部传播,而全局映射恢复长程依赖。该统一设计平衡了表达能力与效率。ImageNet-1K上的实验表明,ViK以线性复杂度实现了具有竞争力的准确率,验证了基于KAN的令牌混合在大规模视觉任务中的有效性。
本文主要贡献如下:
- 提出Vision KAN(ViK),一种无注意力视觉骨干网络,以受KAN启发的令牌混合器替代自注意力,为注意力模块提供高效替代方案。
- 设计MultiPatch-RBFKAN,一种统一模块,融合块级RBF非线性变换、轴向可分离混合与低秩全局映射,平衡表达能力与效率。
- ImageNet-1K实验表明,ViK以线性复杂度实现竞争性准确率,验证了基于KAN的令牌混合在大规模视觉任务中的有效性。
2. 方法
2.1. 预备知识:科尔莫戈罗夫-阿诺德网络
科尔莫戈罗夫-阿诺德表示定理指出,任意多元连续函数可表示为一元函数的组合:f(x1,...,xn)=∑qϕq(∑pϕpq(xp))f(x_{1},\ldots,x_{n}) = \sum_{q}\phi_{q}\Bigl(\sum_{p}\phi_{pq}(x_{p})\Bigr)f(x1,...,xn)=∑qϕq(∑pϕpq(xp)),其中 ϕ(⋅)\phi(\cdot)ϕ(⋅) 为连续一元函数。这表明复杂映射可在不显式建模成对交互的情况下进行逼近,与自注意力形成对比。
Kolmogorov-Arnold Networks(KANs)通过以参数化基函数展开替代固定激活函数来实现该原理:
ϕ(x)=∑j=1Mwj⋅Bj(x),\phi(x) = \sum_{j=1}^{M} w_{j} \cdot B_{j}(x),ϕ(x)=j=1∑Mwj⋅Bj(x),
其中 Bj(⋅)B_{j}(\cdot)Bj(⋅) 为基函数,wjw_{j}wj 为可训练权重,MMM 为基函数数量。与传统MLP相比,KANs提供更强的函数逼近能力与局部可解释性,因每个基函数均可被显式可视化。本文利用该特性设计无注意力视觉骨干网络,在避免二次方自注意力的同时保持高表征能力。
2.2. 整体架构
ViK是一种无注意力视觉骨干网络,采用层次化设计,包含:卷积图像块嵌入、四个阶段的ViK块(空间分辨率递减、通道数递增),以及最终的归一化与分类头。每个ViK块以MultiPatch-RBFKAN替代自注意力,该统一令牌混合器以令牌数量的线性复杂度实现局部到全局的交互,作为二次方注意力的即插即用替代方案。
2.3. 基于KAN的令牌混合器
直接对所有令牌应用全局KAN计算成本过高。因此,ViK采用结构化替代方案:MultiPatch-RBFKAN,将三种互补算子集成至单一令牌混合模块:(a) 块级KAN用于非线性局部建模,(b) 轴向可分离混合以线性成本交换跨块信息,© 低秩全局映射以捕获长程依赖且无二次方开销。
(a) 块级RBFKAN。给定输入特征图,首先将其划分为非重叠的 p×pp \times pp×p 块。依据式(1),其中 B(x)B(x)B(x) 表示KAN中的基函数,我们以径向基函数(RBF)实现 B(x)B(x)B(x) 以建模块内局部非线性交互。具体而言,每个块向量变换为:
ϕ(x)=∑j=1Mwj⋅exp(−∥x−μj∥22σj2),\phi(x) = \sum_{j=1}^{M} w_{j} \cdot \exp\Biggl(-\frac{\|x - \mu_{j}\|^{2}}{2\sigma_{j}^{2}}\Biggr),ϕ(x)=j=1∑Mwj⋅exp(−2σj2∥x−μj∥2),
其中 μj\mu_{j}μj 与 σj\sigma_{j}σj 为可学习的中心与宽度,wjw_{j}wj 为可训练缩放权重。与KANs中常用的需递归计算的B样条基不同,RBF允许所有基激活并行计算,使其在大规模视觉任务中更适配GPU且高效[14]。
(b) 轴向可分离混合。块级KAN捕获块内依赖,但建模跨块交互同样关键。为高效实现此目标,我们沿水平与垂直轴分别应用两个深度卷积(DW),后接全局平均池化(GAP)与基于MLP的重加权:
y^=αh⋅DWh(y)+αw⋅DWw(y),[αh,αw]=Softmax(fMLP(GAP(y))).\begin{aligned} &\hat{y} = \alpha_{h} \cdot DW_{h}(y) + \alpha_{w} \cdot DW_{w}(y), \\ &[\alpha_{h}, \alpha_{w}] = \mathrm{Softmax}(f_{\mathrm{MLP}}(\mathrm{GAP}(y))). \\ \end{aligned}y^=αh⋅DWh(y)+αw⋅DWw(y),[αh,αw]=Softmax(fMLP(GAP(y))).
该机制引入方向敏感的局部混合,使模型能根据图像结构自适应地强调水平或垂直依赖。
© 低秩全局映射。块级局部算子不足以捕获长程依赖。为高效引入全局上下文,我们将每个通道重塑为长度为 NNN 的令牌向量(N=H×WN = H \times WN=H×W),并应用低秩投影:
yglobal=QPy,P∈Rr×N, Q∈RN×r, r≪N.y_{\mathrm{global}} = \mathbf{Q}\mathbf{P}y, \quad \mathbf{P} \in \mathbb{R}^{r \times N}, \; \mathbf{Q} \in \mathbb{R}^{N \times r}, \; r \ll N.yglobal=QPy,P∈Rr×N,Q∈RN×r,r≪N.
此处 P\mathbf{P}P 将空间令牌压缩至秩-rrr 潜在空间,Q\mathbf{Q}Q 将其投影回原空间,实现高效全局信息交换。
2.4. 复杂度分析
设 N=H×WN = H \times WN=H×W 为空间分辨率,ppp 为块大小,CCC 为通道维度,MMM 为基函数数量,r≪Nr \ll Nr≪N 为全局秩。MultiPatch-RBFKAN中各组件的计算成本为:
- 块级RBFKAN:O(N⋅C⋅M⋅F)\mathcal{O}(N \cdot C \cdot M \cdot F)O(N⋅C⋅M⋅F),其中 F=p2F = p^{2}F=p2 为块维度;
- 轴向可分离混合:O(N⋅C⋅k)\mathcal{O}(N \cdot C \cdot k)O(N⋅C⋅k),核大小为 kkk;
- 低秩全局映射:O(N⋅C⋅r)\mathcal{O}(N \cdot C \cdot r)O(N⋅C⋅r)。
因此,每块的总体复杂度为
O(N⋅C⋅(MF+k+r)),\mathcal{O}\big(N \cdot C \cdot (M F + k + r)\big),O(N⋅C⋅(MF+k+r)),
随图像尺寸线性增长。相比二次方自注意力 O(N2⋅C)\mathcal{O}(N^{2} \cdot C)O(N2⋅C),该设计在保持表达能力的同时提供了更高效的无注意力替代方案。
3. 实验与结果
3.1. 实验设置
我们在ImageNet-1K[15]分类基准(128万训练图像,5万验证图像,1000类)上评估ViK。所有模型从零训练300轮,使用AdamW[16]优化器(权重衰减0.05,峰值学习率 1×10−31 \times 10^{-3}1×10−3)。采用现代视觉骨干网络通用的数据增强与优化策略以确保公平比较[3]。报告Top-1准确率、参数量及 224×224224 \times 224224×224 输入分辨率下的GFLOPs。所有实验在4块NVIDIA RTX A6000 GPU上进行。
3.2. 与代表性视觉骨干网络的比较
表1比较了ViK与广泛采用的视觉骨干网络,包括CNN(ResNet[17])、Transformer(ViT[1]、DeiT[2]、PVT[3])及类MLP架构(ResMLP[18])。ViK-Small以仅1.6 GFLOPs达到76.5% Top-1准确率,相比ViT-Ti与DeiT-Ti等早期Transformer有明显提升,计算成本仅略高。与ResMLP-S12及PVT-Tiny相比,ViK-Small在更低FLOPs与参数量下达到相近或更高准确率。
更大规模下,ViK-Base以3.2 GFLOPs达到80.3% Top-1准确率,超越ResNet-50,匹配或超越DeiT-Small、PVT-Small与ResMLP-S24,同时保持显著更低的复杂度。结果表明,ViK在准确率与效率间取得良好平衡,验证了其轻量设计与有效令牌混合策略,且无需依赖注意力机制。
表1. ImageNet-1K分类任务上各架构比较
|-------------------|-----|---------|--------|-----------|
| 模型 | 类型 | 参数量 (M) | GFLOPs | Top-1 (%) |
| ResNet-18 [17] | CNN | 11.7 | 1.8 | 70.6 |
| ViT-Ti/16 [1] | 注意力 | 5.7 | 1.3 | 72.7 |
| DeiT-Tiny [2] | 注意力 | 5.7 | 1.3 | 72.2 |
| PVT-Tiny [3] | 注意力 | 13.2 | 1.9 | 75.1 |
| ResMLP-S12 [18] | MLP | 15 | 3.0 | 76.6 |
| ViK-Small (本文) | KAN | 13.5 | 1.6 | 76.5 |
| ResNet-50 [17] | CNN | 25.6 | 4.1 | 79.2 |
| ViT-S/16 [1] | 注意力 | 22.1 | 4.6 | 78.8 |
| DeiT-Small [2] | 注意力 | 22.1 | 4.6 | 79.8 |
| PVT-Small [3] | 注意力 | 24.5 | 3.8 | 79.8 |
| ResMLP-S24 [18] | MLP | 30 | 6.0 | 79.4 |
| ViK-Base (本文) | KAN | 24.9 | 3.2 | 80.3 |
表2. ViK-Small消融实验。"Activation"表示KAN中基函数类型(RBF、B样条、小波或替换为MLP)。"#Basis"表示基函数数量。
|------|--------|-------|------|-----------|
| 激活函数 | #Basis | 可分离混合 | 全局映射 | Top-1 (%) |
| RBF | 4 | ✗ | ✗ | 74.8 |
| RBF | 6 | ✗ | ✓ | 75.7 |
| RBF | 10 | ✓ | ✓ | 76.4 |
| B样条 | 8 | ✓ | ✓ | 73.8 |
| 小波 | 8 | ✓ | ✓ | 75.2 |
| MLP | - | ✓ | ✓ | 72.1 |
| RBF | 8 | ✗ | ✓ | 74.6 |
| RBF | 8 | ✓ | ✗ | 73.9 |
| RBF | 8 | ✓ | ✓ | 76.5 |
3.3. 消融实验
我们在ViK-Small上进行消融实验,检验激活函数类型、基函数数量及MultiPatch-RBFKAN结构组件的影响。表2总结结果。
基函数数量。增加RBF数量稳步提升准确率(4个基函数时74.8%,10个时76.4%)。性能在 M=8M=8M=8 时达峰值(76.5%),M=10M=10M=10 时轻微下降(76.4%),表明存在饱和并伴随轻微过拟合或优化噪声。鉴于计算成本随 MMM 线性增长,我们采用 M=8M=8M=8 作为准确率与效率间的默认权衡。
激活函数。以不同替代方案替换KAN中的基函数表明,RBF consistently优于B样条与小波基。此外,以同等规模MLP替代KAN导致显著下降(-4.4%)。这支持我们的设计选择:RBF更适配GPU,且在视觉任务中提供更强的非线性逼近能力。
可分离混合与全局映射。移除轴向可分离混合或低秩全局映射均导致性能明显下降(分别从76.5%降至74.6%与73.9%)。结合MLP替换结果,这些发现验证了所提技术通过以轴向混合与全局交互补充局部非线性建模,使KAN更适用于视觉任务。
3.4. 学习到的RBF映射可视化
为深入理解ViK内部工作机制,我们可视化不同阶段与块中RBF学习到的一元函数 ϕ(x)\phi(x)ϕ(x)。每条曲线对应块内特定输入维度。结果表明,RBF有效捕获非线性变换:浅层阶段的函数呈现对局部变化敏感的振荡形态,而深层阶段收敛至更平滑形式,表明向稳定、判别性特征的渐进抽象。这些一元映射提供了清晰的局部可解释性形式。
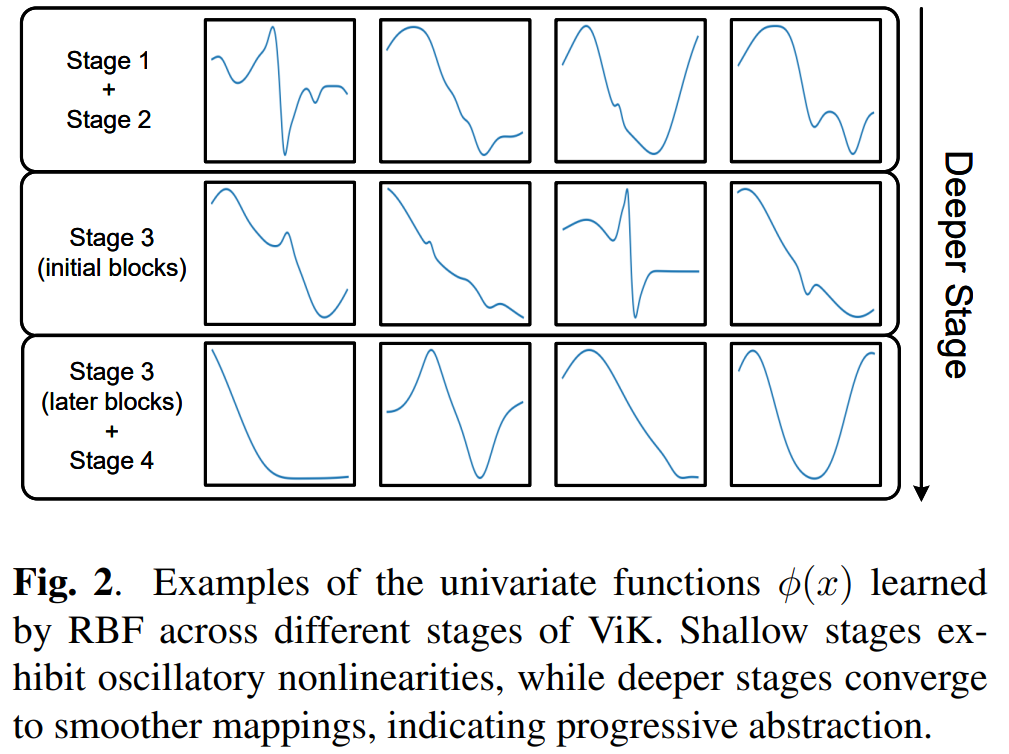
图2. ViK不同阶段学习到的RBF一元函数 \\phi(x) 示例。浅层阶段呈现振荡非线性,深层阶段收敛至更平滑映射,表明渐进式抽象过程。
4. 结论
我们提出ViK,一种无注意力视觉骨干网络,以受科尔莫戈罗夫-阿诺德表示定理启发的基于函数的令牌混合器替代二次方成本的自注意力。所提MultiPatch-RBFKAN将块级非线性RBF展开、轴向可分离混合与低秩全局映射集成至统一模块,实现高效的局部与全局交互。ImageNet-1K上的实验表明,ViK在保持图像尺寸线性复杂度的同时,实现了与经典基于注意力模型相竞争的准确率。这些结果凸显了基于KAN的非线性变换作为视觉骨干网络理论基础的潜力,为构建计算机视觉中的高效架构指明了新方向。
5. 致谢
本工作受国家自然科学基金(资助号62576216与62502320)、广东省重点实验室(资助号2023B1212060076)、广东省自然科学基金(资助号2025A1515010184)、深圳市科技创新委员会项目(资助号JCYJ20240813141424032)及广东省普通高校青年创新人才基金(资助号2024KQNCX042)支持。
6. 参考文献
1\] Alexey Dosovitskiy, Lucas Beyer, Alexander Kolesnikov, et al., "An image is worth 16x16 words: Transformers for image recognition at scale," in International Conference on Learning Representations, 2021. \[2\] Hugo Touvron, Matthieu Cord, Matthijs Douze, et al., "Training data-efficient image transformers \& distillation through attention," in International Conference on Machine Learning. PMLR, 2021, pp. 10347--10357. \[3\] Wenhai Wang, Enze Xie, Xiang Li, et al., "Pyramid vision transformer: A versatile backbone for dense prediction without convolutions," in Proceedings of the IEEE/CVF International Conference on Computer Vision, 2021, pp. 568--578. \[4\] Albert Gu and Tri Dao, "Mamba: Linear-time sequence modeling with selective state spaces," arXiv preprint arXiv:2312.00752, 2023. \[5\] Jasmijn Bastings and Katja Filippova, "The elephant in the interpretability room: Why use attention as explanation when we have saliency methods?," in Proceedings of the Third BlackboxNLP Workshop on Analyzing and Interpreting Neural Networks for NLP, 2020, pp. 149--155. \[6\] Ilya O. Tolstikhin, Neil Houlsby, Alexander Kolesnikov, et al., "MLP-mixer: An all-MLP architecture for vision," Advances in Neural Information Processing Systems, vol. 34, pp. 24261--24272, 2021. \[7\] Weihao Yu, Mi Luo, Pan Zhou, et al., "Metaformer is actually what you need for vision," in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2022, pp. 10819--10829. \[8\] Andrei Nikolaevich Kolmogorov, On the representation of continuous functions of several variables by superpositions of continuous functions of a smaller number of variables, American Mathematical Society, 1961. \[9\] Ziming Liu, Yixuan Wang, Sachin Vaidya, et al., "KAN: Kolmogorov-Arnold networks," in International Conference on Learning Representations, 2025. \[10\] Ziming Liu, Pingchuan Ma, Yixuan Wang, et al., "KAN 2.0: Kolmogorov-Arnold networks meet science," arXiv preprint arXiv:2408.10205, 2024. \[11\] Zhuoqin Yang, Jiansong Zhang, Xiaoling Luo, et al., "Activation space selectable Kolmogorov-Arnold networks," arXiv preprint arXiv:2408.08338, 2024. \[12\] Shaode Yu, Ze Chen, Zhimu Yang, et al., "Exploring Kolmogorov-Arnold networks for realistic image sharpness assessment," in ICASSP 2025-2025 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2025, pp. 1--5. \[13\] Zhuoqin Yang, Jiansong Zhang, Xiaoling Luo, et al., "MedKAN: An advanced Kolmogorov-Arnold network for medical image classification," arXiv preprint arXiv:2502.18416, 2025. \[14\] Ziyao Li, "Kolmogorov-Arnold networks are radial basis function networks," arXiv preprint arXiv:2405.06721, 2024. \[15\] Jia Deng, Wei Dong, Richard Socher, et al., "ImageNet: A large-scale hierarchical image database," in 2009 IEEE Conference on Computer Vision and Pattern Recognition. IEEE, 2009, pp. 248--255. \[16\] Ilya Loshchilov and Frank Hutter, "Decoupled weight decay regularization," in International Conference on Learning Representations, 2019. \[17\] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun, "Deep residual learning for image recognition," in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, pp. 770--778. \[18\] Hugo Touvron, Piotr Bojanowski, Mathilde Caron, et al., "ResMLP: Feedforward networks for image classification with data-efficient training," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 45, no. 4, pp. 5314--5321, 2022.