Sensing in Bistatic ISAC Systems With Clock Asynchronism

信号建模

文章目录

• • • [Challenges in Addressing Clock Asynchronism for Sensing](#Challenges in Addressing Clock Asynchronism for Sensing)
• [Single-Node Bistatic Sensing Techniques](#Single-Node Bistatic Sensing Techniques)
• • [Offset Cancellation Methods: Delay-Domain Processing Techniques](#Offset Cancellation Methods: Delay-Domain Processing Techniques)
  • • [Cross-Antenna Cross-Correlation](#Cross-Antenna Cross-Correlation)
    • [Cross-Antenna Signal Ratio](#Cross-Antenna Signal Ratio)
  • [Offset Cancellation Methods: Delay-Domain Processing Techniques](#Offset Cancellation Methods: Delay-Domain Processing Techniques)
  • [Offset Estimation Methods](#Offset Estimation Methods)
  • [Comparisons and Remarks](#Comparisons and Remarks)
• [Future Research Directions and Open Problems](#Future Research Directions and Open Problems)
• • [Construction of a Reference Path](#Construction of a Reference Path)
  • [Sensing of Multiple Targets](#Sensing of Multiple Targets)
  • [Mobility of the Nodes](#Mobility of the Nodes)
  • [Coherently Combine Multiple Rxs](#Coherently Combine Multiple Rxs)
  • [Joint Spatial-Delay-Frequency-Domain Processing](#Joint Spatial-Delay-Frequency-Domain Processing)
  • [Open Dataset for Bistatic Sensing Research and Development](#Open Dataset for Bistatic Sensing Research and Development)

我们现在将这些偏移量合并到多输入多输出（MIMO）正交频分复用（OFDM）积分感知与通信（ISAC）信号模型中。我们注意到， MIMO-OFDM 已被广泛应用于现代蜂窝网络，如 4G 和 5G 。可以预见它将在 6G 中继续盛行。考虑一个双节点 MIMO-OFDM 通信系统，其中发送和接收节点各配备一个均匀线性阵列。发送（ Tx ）和接收（ Rx ）阵列分别具有 M M M （ N N N ）个天线，且天线间距为半波长。它们的导向矢量可以表示为 a ( x , α ) = [ 1 , e j π sin ⁡ ( α ) , ... , e j ( x − 1 ) π sin ⁡ ( α ) ] T \mathbf{a}(x, \alpha) = [1, e^{j\pi\sin(\alpha)}, \dots, e^{j(x-1)\pi\sin(\alpha)}]^{\text{T}} a(x,α)=[1,ejπsin(α),...,ej(x−1)πsin(α)]T ，其中 x = M x = M x=M 或 N N N ， α \alpha α 可以是出发角（ AoD ）或到达角（ AoA ）。对于 OFDM 传输，带宽为 B B B 的频带被划分为 S S S 个子载波。那么子载波间隔为 Δ f = B / S \Delta_f = B/S Δf=B/S ，这导致 OFDM 符号周期为

T O = T 0 + T cp T_O = T_0 + T_{\text{cp}} TO=T0+Tcp ，其中 T 0 = 1 / Δ f = S / B T_0 = 1/\Delta_f = S/B T0=1/Δf=S/B ，并且 T cp T_{\text{cp}} Tcp 是循环前缀的周期。

考虑 k = 1 , ... , K k = 1, \dots, K k=1,...,K 个接收到的 OFDM 符号，它们以 T s T_s Ts 的间隔等距分布。将定时偏移（ TO ）和（残留的）载波频率偏移（ CFO ）分别记为 τ o , k \tau_{o,k} τo,k 和 f o , k f_{o,k} fo,k 。此外，我们使用复数值 β k \beta_k βk 来反映随机相位偏移以及所有其他（对感知造成影响的）硬件不完美因素，例如自动增益控制、射频链路不平衡等。请注意，所有这些干扰因素都取决于发送端与接收端之间的相对异步性；因此，它们特定于每一对收发端。此外，它们在 OFDM 符号级别上是随时间变化的，如其下标 k k k 所示。假设存在 L L L 条路径，其中第 l l l （ l = 1 , ... , L l = 1, \dots, L l=1,...,L ）条路径的复数路径增益、传播延迟、多普勒频率、到达角和出发角分别由 b l b_l bl 、 τ l \tau_l τl 、 f D , l f_{D,l} fD,l 、 ϕ l \phi_l ϕl 和 θ l \theta_l θl 给出。在第 i i i 个子载波和第 k k k 个 OFDM 符号处的无噪信道频率响应（ CFR ）矩阵可以表示为

H i , k = β k ∑ l = 1 L b l e − j 2 π i ( τ l + τ o , k ) Δ f e j 2 π ( f D , l + f o , k ) k T s a ( N , ϕ l ) a T ( M , θ l ) = β k e − j 2 π i Δ f τ o , k e j 2 π f o , k k T s ⏟ ξ i , k ∑ l = 1 L b l e − j 2 π i Δ f τ l e j 2 π f D , l k T s a ( N , ϕ l ) a T ( M , θ l ) \begin{align} \mathbf{H}{i,k} &= \beta_k \sum{l=1}^L b_l e^{-j2\pi i(\tau_l + \tau_{o,k})\Delta_f} e^{j2\pi (f_{D,l} + f_{o,k})k T_s} \mathbf{a}(N, \phi_l) \mathbf{a}^{\text{T}}(M, \theta_l) \tag{1} \\ &= \underbrace{\beta_k e^{-j2\pi i \Delta_f \tau_{o,k}} e^{j2\pi f_{o,k} k T_s}}{\xi{i,k}} \sum_{l=1}^L b_l e^{-j2\pi i \Delta_f \tau_l} e^{j2\pi f_{D,l} k T_s} \mathbf{a}(N, \phi_l) \mathbf{a}^{\text{T}}(M, \theta_l) \tag{2} \end{align} Hi,k=βkl=1∑Lble−j2πi(τl+τo,k)Δfej2π(fD,l+fo,k)kTsa(N,ϕl)aT(M,θl)=ξi,k βke−j2πiΔfτo,kej2πfo,kkTsl=1∑Lble−j2πiΔfτlej2πfD,lkTsa(N,ϕl)aT(M,θl)(1)(2)

这里作出了三个假设。

• 1）所有发射天线共享一个公共本振（ LO ），所有接收天线也是如此。
• 2）由多普勒频率和 CFO 引起的符号内相位变化可以忽略不计。
• 3）目标的感知参数在极短的相干处理间隔内可以认为是恒定的，例如在几毫秒到几十毫秒的周期内 [7] 。

因此，为了简洁起见，在 H i , k \mathbf{H}{i,k} Hi,k 中省略了它们对符号索引 k k k 的依赖。这三个假设在大多数雷达和 ISAC 工作中是典型且被广泛使用的。在式（2）中，几个干扰系数被合并为一个单一的项，表示为 ξ i , k \xi{i,k} ξi,k 。

（2）式中的 L L L 条路径可以分为静态路径和动态路径，这取决于在观测时间段内底层散射体是否在移动。请注意，一个观测周期可以包含多个 OFDM 时隙或数据包。

• 对于静态路径，我们有 f D , l = 0 f_{D,l} = 0 fD,l=0 ，并且 τ l \tau_l τl 、 θ l \theta_l θl 、 ϕ l \phi_l ϕl 在整个观测周期内保持恒定。
• 对于动态路径 f D , l ≠ 0 f_{D,l} \neq 0 fD,l=0 ，感知参数可以被认为在极短的处理间隔内是恒定的，正如在（2）式中所做的那样。

在观测周期内，感知参数可能会发生变化，如后面"偏移消除方法：空域处理"部分所示。这些特性是"单节点双基感知技术"部分提出的一些方法的关键。

由时钟异步引起的偏移通常会降低感知性能。

• 一方面， TO 和 CFO 会导致延迟和多普勒频率估计中出现模糊值，进而导致测距和速度估计中的模糊。
• 另一方面，随机相位偏移使得直接对多个 CSI 测量结果进行相干处理变得不可能；

注意， CSI 的功率可以被用来在时域内联合处理多个测量结果。此外，雷达感知中流行的先进感知技术，例如微多普勒频谱图 [8] ，也受到 CFO 的严重影响， CFO 会破坏多普勒特征。微多普勒包含关于目标的细粒度信息，包括多个移动部分。它是许多应用的关键组成部分，例如目标识别、人类活动识别和人员身份验证等 [2] 。我们将使用微多普勒的质量作为可能的评估标准之一，以及作为比较各种 CFO 消除方法的一种手段。

Challenges in Addressing Clock Asynchronism for Sensing

在通信系统中，上述由时钟异步引起的偏移通常通过使用成熟的算法 [9], [10], [11] 来补偿。此外，对于通信而言，不需要将定时偏移（ TO ）与传播延迟分离开来。接收机（ Rx ）确定精细定时，剩余的 TO 被包含在信道估计中，并通过信道均衡消除。对于载波频率偏移（ CFO ），可以通过使用例如两个重复序列 [11] 来进行估计和补偿，而残留 CFO 的影响，连同微小的多普勒频移，可以被忽略，或者通过估计和补偿它们的累积相位偏移来缓解。

与数据通信通常可以有效地处理偏移不同，减轻这些偏移对感知的影响具有挑战性。对于感知，必须分离 TO 以获得传播延迟的纯净估计。 CFO 和 f D f_D fD 也需要分离，但这无法通过传统的 CFO 估计技术来实现。残留 CFO 的值可能接近待估计的多普勒频移，如果不妥善处理，会导致较大的多普勒估计误差。因此，解决时钟异步问题是双基感知中的一个关键挑战。

有几种方法可以潜在地解决这个问题 [6] ，例如使用全球 GPS 驯服时钟（a global GPS disciplined clock，GPSDO ）或应用基于单节点的信号处理技术（single-node-based signal processing techniques）。

• 具有高达 5.5 ns 定时精度的 GPSDO 成本可能达到 1,000 美元 [6] 。它还需要开阔的天空视野才能运行，且体积相对较大。因此，实际上无法将其集成到每个移动设备中。
• 相比之下（In comparison），基于单节点的处理在解决异步挑战方面可能更实用且更有前景，且成本要低得多，因为它不需要额外的设备或多节点之间复杂的信息交换。

然而， GPSDO 并非没有优点。在大型购物中心等场景中，投资高质量的 GPSDO 可以通过有线方式向许多终端分发精确时钟，从而提高时钟稳定性，以实现更好的双基感知。本项工作主要关注解决时钟异步问题的信号处理技术。接下来，我们将对这些技术进行深入概述。

"Single-node-based signal processing techniques"（基于单节点的信号处理技术）指的是在双基（Bistatic）感知场景中，仅依靠接收端（Rx）这一单个节点自身的算法能力，来解决收发设备之间时钟不同步（Clock Asynchronism）问题的一类方法。

Single-Node Bistatic Sensing Techniques

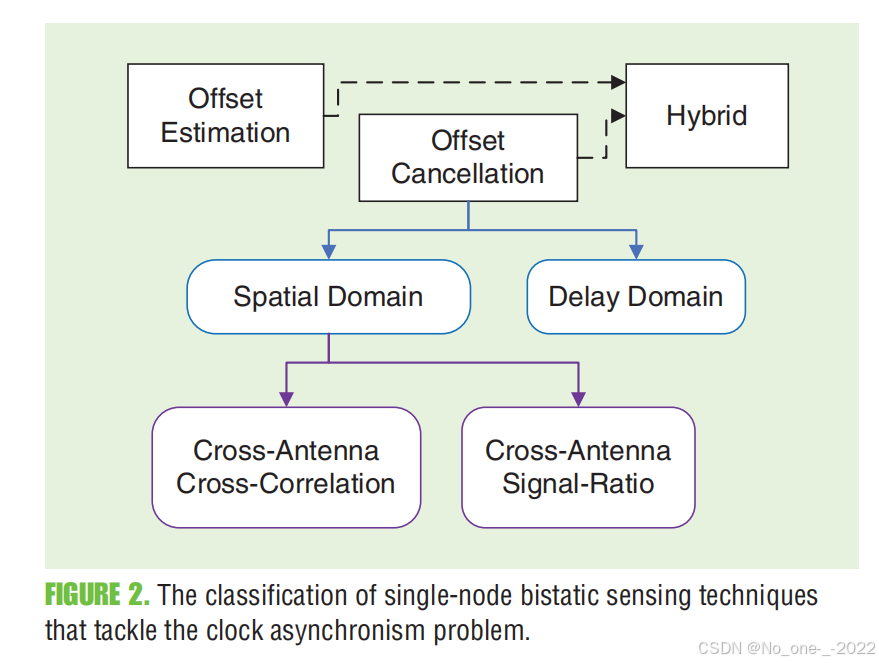
从信号处理的角度来看，可以通过消除（2）式中 ξ i , k \xi_{i,k} ξi,k 的贡献来解决双基感知中的时钟异步问题。这种消除可以通过在不估计具体数值的情况下进行抵消来实现，也可以通过估计随后进行补偿来实现；它还可以在不同的域中完成，例如空域和时延域。根据"消除"是如何实现的，我们将文献中发现的技术组织并展示为三种主要类型的方法，如图 2 所总结的那样。

1. 偏移抵消方法（Offset cancellation methods） [12], [13], [14], [15], [16], [17], [18] ：这种方法主要应用于空域 [12], [13], [14], [15], [16], [17] ，利用了时钟异步项 ξ i , k \xi_{i,k} ξi,k 在天线间是公共的这一事实，并且可以通过跨天线处理（包括互相关和信号比值）来减轻其影响。最近，一种在时延域中的偏移抵消方法被提出 [18] ，它不需要多个接收天线。

2. 偏移估计与抑制（Offset estimation and suppression） [19], [20], [21] ：这些方法分别估计干扰项（the nuisance terms），即（namely） τ o , k \tau_{o,k} τo,k 和 f o , k f_{o,k} fo,k ，或者将它们的综合影响 ξ i , k \xi_{i,k} ξi,k 作为一个整体进行估计，然后减轻它们的影响以促进无模糊感知。

3. 偏移抵消与估计的混合方法（Hybrid of offset cancellation and estimation） [22] ：这类方法估计并抑制 TO ，而 CFO 则类似于第 1) 点被抵消掉。由于干扰项 ξ i , k \xi_{i,k} ξi,k 对所有传播路径都是公共的，因此利用信道冲激响应（ CIR ）的时延域处理通过相关性高效地获得 TO 。然后使用一个参考静态路径来抵消相位偏移，而不需要接收端具备多个天线。

每种技术都有特定的特征、优缺点，它们的适用性取决于感知目标。例如（For example），某些技术可能适合获取特定参数的估计值，如 AoA 和时延。但是（Still），它们可能无法在时域上实现相干信号处理。接下来，我们将更详细地回顾这三种类型中的一些代表性工作。请注意，我们将基于用于解决时钟异步和估计多径传播参数（即路径的复数路径增益、传播时延、多普勒频率、 AoA 和 AoD ，如 (2) 中的 CFR 模型（Channel Frequency Response Model）所述）的策略来分析不同的方法。

关于环境位置和运动的目标信息可以通过对估计的传播参数应用进一步的处理步骤来获得。该处理可以独立于估计过程。对于这方面，我们建议感兴趣的读者参考 [22] 。

Offset Cancellation Methods: Delay-Domain Processing Techniques

Cross-Antenna Cross-Correlation

为了清晰地回顾跨天线互相关（cross-antenna cross-correlation，CACC） [12] 的核心思想，我们通过假设单个发射天线（即 M = 1 M = 1 M=1 ）来简化 (1) 中的 H i , k \mathbf{H}_{i,k} Hi,k 。那么，第 n n n 个天线在第 i i i 个子载波和第 k k k 个 OFDM 符号处的信道系数可以写为

H i , k , n = ξ i , k ∑ l = 1 L b l e − j 2 π i Δ f τ l e j 2 π f D , l k T s e j n π sin ⁡ ( ϕ l ) . (3) H_{i,k,n} = \xi_{i,k} \sum_{l=1}^L b_l e^{-j2\pi i\Delta_f \tau_l} e^{j2\pi f_{D,l} k T_s} e^{jn\pi \sin(\phi_l)}. \tag{3} Hi,k,n=ξi,kl=1∑Lble−j2πiΔfτlej2πfD,lkTsejnπsin(ϕl).(3)

顾名思义， CACC 对两个天线之间的信道系数进行共轭互相关。按照惯例，一个天线被视为参考天线并给定索引 n = 0 n = 0 n=0 。让我们考虑（Let us consider） H i , k , 0 H_{i,k,0} Hi,k,0 （即 n = 0 n = 0 n=0 ）与 H i , k , n H_{i,k,n} Hi,k,n （其中 n ≠ 0 n \neq 0 n=0 ）之间的互相关。基于 H i , k , n H_{i,k,n} Hi,k,n 的 CACC 可以计算为

r i , k , n = H i , k , 0 H i , k , n ∗ ≈ ∑ l 1 = 1 L ∑ l 2 = 1 L b l 1 b l 2 ∗ e − j 2 π i Δ f ( τ l 1 − τ l 2 ) e j 2 π ( f D , l 1 − f D , l 2 ) k T s e − j n π sin ⁡ ( ϕ l 2 ) (4) r_{i,k,n} = H_{i,k,0} H_{i,k,n}^* \approx \sum_{l_1=1}^L \sum_{l_2=1}^L b_{l_1} b_{l_2}^* e^{-j2\pi i \Delta_f (\tau_{l_1} - \tau_{l_2})} e^{j2\pi (f_{D,l_1} - f_{D,l_2}) k T_s} e^{-jn\pi \sin(\phi_{l_2})} \tag{4} ri,k,n=Hi,k,0Hi,k,n∗≈l1=1∑Ll2=1∑Lbl1bl2∗e−j2πiΔf(τl1−τl2)ej2π(fD,l1−fD,l2)kTse−jnπsin(ϕl2)(4)

这里的近似是由于 ∣ ξ i , k ∣ 2 ≈ 1 |\xi_{i,k}|^2 \approx 1 ∣ξi,k∣2≈1 。相位偏移从 r i , k , n r_{i,k,n} ri,k,n 中被完全消除。然而，它的交叉乘积也通过创建虚拟路径引入了更多的未知参数。文献中已经提出了许多设计，以有效地从 r i , k , n r_{i,k,n} ri,k,n 中估计真实的目标参数 [12], [13], [14] 。

在 [12] 和 [13] 中，假设存在强的视距（ LoS ），考虑单个动态路径，并且 (3) 中的 L L L 条路径被分为两组：静态路径和单个动态路径。那么， (4) 中的 r i , k , n r_{i,k,n} ri,k,n 有四个主要分量。

1. 天线 n = 0 n=0 n=0 上的静态路径乘以天线 n n n 上静态路径的共轭：在存在强 LoS 的情况下，该乘积随时间近似恒定，并且可以使用高通滤波器进行抑制。
2. 天线 n = 0 n=0 n=0 上的动态路径乘以天线 n n n 上动态路径的共轭：该乘积比涉及强 LoS 主导的静态路径的其他三项要弱得多，因此可以忽略。
3. 天线 n = 0 n=0 n=0 上的静态路径乘以天线 n n n 上动态路径的共轭：该乘积包含动态路径的感知参数，由于共轭运算，其符号与实际参数相反。其功率也由天线 0 0 0 上的静态路径主导。
4. 天线 0 0 0 上的动态路径乘以天线 n n n 上静态路径的共轭：该乘积反映了真实的感知参数，其功率由天线 n n n 上的静态路径主导。

• 基于前四个分量的特征，文献 [12] 提出了一种加减感知方法（an add-minus sensing method，AMS）。正如前面提到的最后两个分量的功率特征所示，向天线 n n n 加上一个正值可以增强最后一个分量，而从天线 0 减去一个正值可以削弱包含虚拟目标的第三个分量。这进而有助于基于 CACC 估计实际目标的感知参数。

  通过人为增强天线 n n n的静态能量（让真实目标信号更亮），同时人为削弱天线0的静态能量（让假目标信号更暗），我们就可以在最终的运算结果中，更容易地把真实目标提取出来，压制住那个干扰视线的假目标。

• 与 AMS 不同，文献 [13] 中的工作提出利用前面列出的其他分量来减轻不必要的项。特别是，文献 [13] 的作者揭示了，在存在强 LoS 路径的情况下，所有相邻天线上的互相关的二阶循环差分可用于估计一阶差分中与虚拟目标相关的项。然后可以使用该估计值来减轻一阶差分中虚拟目标的影响，从而利用 root-MUSIC 算法实现无模糊的多普勒频率估计。

• 与上述专注于单个动态路径的工作不同，文献 [14] 中的工作基于 CACC 结果构建新信号，使得构建的信号由与动态路径数量相同的基张成。随后提出了一种镜像 MUSIC 算法来估计多个目标的多普勒频率。

  如果利用多个快照仅生成 AoA 估计，我们可以计算传统的空间相关矩阵 ( 1 / K ) ∑ k = k 0 k 0 + K − 1 H i , k H i , k H (1/K)\sum_{k=k_0}^{k_0+K-1} \mathbf{H}{i,k} \mathbf{H}{i,k}^H (1/K)∑k=k0k0+K−1Hi,kHi,kH ，其中由于隐式应用了 CACC ，所有偏移都被抵消了。因此，可以应用传统的频谱分析技术（如 MUSIC ）来获得估计值。然而，需要注意的是，来自 K K K 个快照的互相关项被平均作为输出，从而无法应用带通滤波器来消除静态分量。

• 幸运的是，如文献 [20] 所示，所有静态分量都可以在 MUSIC 谱域中作为一个元素进行估计，因为它们在所有快照中表现为一个常数矢量。

Cross-Antenna Signal Ratio

与 CACC 类似，跨天线信号比值（cross-antenna signal ratio，CASR） [15] 利用了这样一个事实：由异步引起的相位偏移对于所有接收天线都是公共的；两个天线之间的比值可以抵消异步因子，即 (2) 中的 ξ i , k \xi_{i,k} ξi,k ，从而促进无模糊感知。类似于我们在 (4) 中获得 r i , k , n r_{i,k,n} ri,k,n 的方式， H i , k , n H_{i,k,n} Hi,k,n 与 H i , k , 0 H_{i,k,0} Hi,k,0 之间的比值提供了以下 CASR 公式：

ρ i , k , n = H i , k , n H i , k , 0 = ∑ l = 1 L b l e − j 2 π i Δ f τ l e j 2 π f D , l k T s e j n π sin ⁡ ( ϕ l ) ∑ l = 1 L b l e − j 2 π i Δ f τ l e j 2 π f D , l k T s (5) \rho_{i,k,n} = \frac{H_{i,k,n}}{H_{i,k,0}} = \frac{\sum_{l=1}^L b_l e^{-j2\pi i\Delta_f \tau_l} e^{j2\pi f_{D,l} k T_s} e^{jn\pi \sin(\phi_l)}}{\sum_{l=1}^L b_l e^{-j2\pi i\Delta_f \tau_l} e^{j2\pi f_{D,l} k T_s}} \tag{5} ρi,k,n=Hi,k,0Hi,k,n=∑l=1Lble−j2πiΔfτlej2πfD,lkTs∑l=1Lble−j2πiΔfτlej2πfD,lkTsejnπsin(ϕl)(5)

其中 ξ i , k \xi_{i,k} ξi,k 被抵消了，但感知参数出现在了分母中。后者的变化使得 CASR 成为感知参数的非线性模型，从而使许多基于线性感知模型的传统感知方法失效。

假设存在单个动态路径，并将所有静态路径合并为一个单一项（Assuming a single dynamic path and combining all static paths into a single term），前面提到的 CASR 公式可以简化为

ρ i , k , n = b ~ e j n π sin ⁡ ( ϕ 1 ) e j 2 π f D , 1 k T s + A b ~ e j 2 π f D , 1 k T s + B (6) \rho_{i,k,n} = \frac{\tilde{b} e^{jn\pi \sin(\phi_1)} e^{j2\pi f_{D,1} k T_s} + \mathcal{A}}{\tilde{b} e^{j2\pi f_{D,1} k T_s} + \mathcal{B}} \tag{6} ρi,k,n=b~ej2πfD,1kTs+Bb~ejnπsin(ϕ1)ej2πfD,1kTs+A(6)

其中 A \mathcal{A} A 和 B \mathcal{B} B 独立于 f D , 1 f_{D,1} fD,1 。文献 [15] 指出，如果 A b ~ e j 2 π f D , 1 k T s − B b ~ e j n π sin ⁡ ( ϕ 1 ) ≠ 0 \mathcal{A}\tilde{b}e^{j2\pi f_{D,1}k T_s} - \mathcal{B}\tilde{b}e^{jn\pi \sin(\phi_1)} \neq 0 Ab~ej2πfD,1kTs−Bb~ejnπsin(ϕ1)=0 ，则 ρ i , k , n \rho_{i,k,n} ρi,k,n 是 e j 2 π f D , 1 k T s e^{j2\pi f_{D,1} k T_s} ej2πfD,1kTs 的莫比乌斯变换（ Mobius transformation ）。通过分析莫比乌斯变换中涉及的平移、复数求逆和乘法操作的不同影响，结果表明 CASR 和 e j 2 π f D , 1 k T s e^{j2\pi f_{D,1} k T_s} ej2πfD,1kTs 在复数域中跨越相同的角度范围。在 [15] 中考虑的单个动态路径的情况下，绝对 CASR 呈现出类正弦振荡，并且可以通过在复数域中旋转 CASR 来增强振荡的峰峰值幅度。在搜索最佳旋转之后，使用绝对 CASR 在符号上的自相关来估计动态路径的多普勒频率。

在 [16] 中，提出了三种基于 CSI 比值的估计方法来估计单个目标的多普勒频率。第一种方法估计 ρ i , k , n \rho_{i,k,n} ρi,k,n 在时间间隔（比如 Δ t \Delta_t Δt ）内的角度变化，然后执行线性拟合以将相位变化率估计为多普勒频率。请注意，为了估计随时间变化的角度变化，必须首先估计由 ρ i , k , n \rho_{i,k,n} ρi,k,n 生成的圆弧/圆的中心。第二种方法建立在 ρ i , k , n \rho_{i,k,n} ρi,k,n 和 e j 2 π f D , 1 k T s e^{j2\pi f_{D,1} k T_s} ej2πfD,1kTs 之间相同的周期性之上。它建议通过搜索导致 ρ i , k , n \rho_{i,k,n} ρi,k,n 的角度最接近的时间间隔来估计 ρ i , k , n \rho_{i,k,n} ρi,k,n 在 k k k 上的周期性。第三种方法利用 ρ i , k , n \rho_{i,k,n} ρi,k,n 的周期性，并搜索导致 ρ i , k , n \rho_{i,k,n} ρi,k,n 与其延迟版本之间互相关最小的时间间隔。

当在公共 Widar2.0 Wi-Fi 数据集 [23] 上进行测试时，文献 [16] 中提出的三种多普勒估计方法在室内场景中的表现优于基于 CACC 的 IndoTrack [12] ，如图 3 所示。图中的结果是基于开放数据集 Widar [23] 获得的。这里使用的数据是在教室中收集的，其中一个人在方形轨道上行走，通信 Tx 和 Rx 固定。因此，多普勒频率随时间变化。我们要指出的是，图中的每个估计值都是基于有限数量的连续符号获得的，其中感知参数近似恒定。因此， (1) 中的信号模型适用于每个估计。 CACC 的主要问题是镜像动态路径，如图 3 所示，这可能导致错误但对称的移动路径检测。 CASR 可以缓解这个问题，特别是在单动态路径场景中。

最近，文献 [24] 通过推导闭式克拉美-罗下界表达式，提供了使用 CASR 方法进行多普勒感知的性能边界。揭示了众多系统参数对多普勒感知的影响。此外，还基于这些见解进行了波形优化，实现了大幅的性能提升。

为了利用 CSI 比值进行多目标感知，文献 [17] 提出了一种基于泰勒级数的方法。该工作考虑了包含多个动态目标的通用模型。推导了 CSI 比值的二阶复泰勒级数，其形式为待估计感知参数矢量的闭式表达式。这揭示了不同快照之间 CSI 比值差异中蕴含的独特模式，从而促进了超分辨率多目标多普勒感知。相反，文献 [19] 采用独立成分分析来分离多个目标对 CFR 的贡献，从而将 CASR 扩展到多目标场景，但这会带来更高的计算成本。

我们需要指出的是（We remark that），当使用多个发射天线时，可以在感知接收（ Rx ）端创建虚拟天线信道，这与传统的 MIMO 雷达处理类似。参考 (1) 中的信道矩阵，可以看到对矩阵进行向量化可以生成一个新的导向矢量，它可以看作是原始导向矢量的克罗内克积。向量化信道矢量的每个元素都可以视为一个虚拟信道的 CSI 。尽管如此，我们注意到这种空域处理并没有改变由随机偏移引起的干扰这一事实，即 (1) 中的 ξ i , k \xi_{i,k} ξi,k ，对于 CSI 中的所有元素仍然是公共的。这使得我们能够继续应用本节中回顾的偏移消除方法来抑制由时钟异步引起的随机偏移。然而，在抵消偏移之后，基于虚拟信道的感知方法可能需要进一步的研究。

However, sensing methods based on virtual channels after canceling offsets may need further investigation.

Offset Cancellation Methods: Delay-Domain Processing Techniques

时延域技术通过利用定时偏移（TO）和载波频率偏移（CFO）在不同信号传播路径中不发生变化（因为它们取决于接收机（ Rx ）硬件）这一事实来消除它们。因此，此类技术独立于发送端（Tx）或接收端设备上的天线数量，并且它们可以在单输入单输出系统（其中跨天线技术不适用）或配备单个相控阵的系统中工作。

为了说明这一点，我们使用 M = 1 M = 1 M=1 和 N = 1 N = 1 N=1 来简化 (2) 中给出的 OFDM 系统的 CFR 模型。子载波 i i i 处第 k k k 个符号的信道增益写为

H i , k = ξ i , k ∑ l = 1 L b l e − j 2 π i Δ f τ l e j 2 π f D , l k T s . (7) H_{i,k} = \xi_{i,k} \sum_{l=1}^L b_l e^{-j2\pi i\Delta_f \tau_l} e^{j2\pi f_{D,l} k T_s}. \tag{7} Hi,k=ξi,kl=1∑Lble−j2πiΔfτlej2πfD,lkTs.(7)

如果收发端配备了连接到同一射频链路的多天线相控阵，上述模型同样成立。在这种情况下，我们认为整体的波束赋形增益包含在系数 b l b_l bl 中。方程（7）表明，补偿相位偏移的一种可行方法是使用其中一条传播路径作为参考。由于 ξ i , k \xi_{i,k} ξi,k 被抵消，关于参考路径的相位差仅取决于传播路径的延迟和多普勒频移。因此，只要参考路径的延迟和多普勒是已知的（例如，因为它是静态的，所以不存在多普勒频移，并且可以使用定位技术对其延迟进行一次性估计），就可以使用低复杂度算法来执行感知参数的估计。这个想法类似于"偏移抵消方法：空域处理"部分中讨论的空域（即，跨天线）处理技术背后的想法，但它不需要使用多根天线，而是利用了时延域中的多径分辨率（leveraging multipath resolution in the delay domain instead）。

参考路径对 CFR 的贡献 H ˉ i , k \bar{H}{i,k} Hˉi,k 表示为 H ˉ i , k = ξ i , k b 1 e − j 2 π i Δ f τ 1 e j 2 π f D , 1 k T s \bar{H}{i,k} = \xi_{i,k}b_1e^{-j2\pi i\Delta_f\tau_1}e^{j2\pi f_{D,1}k T_s} Hˉi,k=ξi,kb1e−j2πiΔfτ1ej2πfD,1kTs ，其中我们按照惯例假设参考路径的索引为 l = 1 l = 1 l=1 。无偏移的 CFR H ^ i , k \hat{H}_{i,k} H^i,k 是通过将 (7) 中的 CFR 乘以参考路径 CFR 的复共轭（以获得相位差）来获得的，即，

H ^ i , k = H i , k H ˉ i , k ∗ = b 1 ∑ l = 1 L b l e − j 2 π i Δ f ( τ l − τ 1 ) e j 2 π ( f D , l − f D , 1 ) k T s . (8) \hat{H}{i,k} = H{i,k}\bar{H}{i,k}^* = b_1 \sum{l=1}^L b_l e^{-j2\pi i\Delta_f(\tau_l-\tau_1)} e^{j2\pi (f_{D,l}-f_{D,1})k T_s}. \tag{8} H^i,k=Hi,kHˉi,k∗=b1l=1∑Lble−j2πiΔf(τl−τ1)ej2π(fD,l−fD,1)kTs.(8)

在 (8) 中，路径 l l l 的延迟和多普勒参数已被相对量 τ l − τ 1 \tau_l - \tau_1 τl−τ1 和 f D , l − f D , 1 f_{D,l} - f_{D,1} fD,l−fD,1 所取代。然而，与空域技术（见"偏移抵消方法：空域处理"部分）不同的是（unlike in spatial-domain techniques），这里并没有增加后续参数估计的复杂度，原因有两点。

• 首先，在视距（ LoS ）和非视距（ NLoS ）条件下，如果收发机之间的距离已知，则可以通过利用著名的双基雷达几何结构轻松使用相对延迟 τ l − τ 1 \tau_l - \tau_1 τl−τ1 来跟踪目标（例如，参见 [25] ）。
• 其次，如果用于补偿 CFO 的参考路径是静态的，我们有 f D , 1 = 0 f_{D,1} = 0 fD,1=0 ，这意味着 (8) 中的相对多普勒频移等于绝对多普勒频移。这允许直接估计多普勒频率，避免了相对频移的模糊性。

在下文中，我们将详细介绍 SHARP（we detail SHARP） ，这是 [18] 中用于在 5-GHz Wi-Fi 频段上运行的 OFDM IEEE 802.11ac/ax 系统的时延域相位偏移补偿技术。时延域处理也用于 [22] 中，其中包括一种混合方法，将在"混合方法"部分中介绍。

在 SHARP 中，最强的传播路径被用作参考，因为可以合理地假设它对应于视距（ LoS ）路径，并且在较短的采集时间内几乎保持不变。在 sub-7-GHz 系统中应用时延域相位偏移消除的主要挑战在于，由于传输带宽较小（通常为 40 至 160 MHz ），它们的多径分辨率较低。这使得很难通过简单地在时间维度上应用傅里叶逆变换来分离多个传播路径。为了应对这一挑战， [18] 提出了一种基于压缩感知优化问题的定制多径分辨率技术

r k = arg ⁡ min ⁡ r ~ ∥ H k − T r ~ ∥ 2 2 + λ ∥ r ~ ∥ 1 (9) \mathbf{r}k = \arg\min{\tilde{\mathbf{r}}} \|\mathbf{H}_k - \mathbf{T}\tilde{\mathbf{r}}\|_2^2 + \lambda \|\tilde{\mathbf{r}}\|_1 \tag{9} rk=argr~min∥Hk−Tr~∥22+λ∥r~∥1(9)

其中 H k = [ H 0 , k , ... , H S − 1 , k ] T \mathbf{H}k = [H{0,k}, \dots, H_{S-1,k}]^{\text{T}} Hk=[H0,k,...,HS−1,k]T ， T \mathbf{T} T 是一个 ( S × L ′ ) (S \times L') (S×L′) 维的字典矩阵，其元素 ( i , l ) (i, l) (i,l) 设置为 T i , l = e − j 2 π i τ l , tot / T O T_{i,l} = e^{-j2\pi i\tau_{l,\text{tot}}/T_O} Ti,l=e−j2πiτl,tot/TO ，并且带有 l = 0 , ... , L ′ − 1 l = 0, \dots, L' - 1 l=0,...,L′−1 的 τ l , tot \tau_{l,\text{tot}} τl,tot 是一组候选的组合 TO ，包括传播延迟 τ l \tau_l τl 和 TO τ o , k \tau_{o,k} τo,k 。 L ′ > L L' > L L′>L 是定义矩阵 T \mathbf{T} T 中包含的可能多径分量网格的参数。向量 r k \mathbf{r}k rk （以及相应的 r ~ \tilde{\mathbf{r}} r~ ）是 L ′ L' L′ 维的，代表了偏移的与子载波无关的项，包括 CFO 和随机相位偏移，即 r k \mathbf{r}k rk 的第 l l l 个元素为 r k , l = β k e j 2 π f o , k k T s b l r{k,l} = \beta_k e^{j2\pi f{o,k} k T_s} b_l rk,l=βkej2πfo,kkTsbl 。

请注意（Note that），在我们于 (2) 中的模型中， b l b_l bl 包含一个载波相位项 e − j 2 π f c τ l e^{-j2\pi f_c \tau_l} e−j2πfcτl ，其中 f c f_c fc 是载波频率，而这在 [18] 中是明确写出的。通过求解 (9) 获得的向量 r k \mathbf{r}k rk 中非零项的位置指示了 L ′ L' L′ 个分量中估计出的多径分量。对于每个 OFDM 子载波 i i i ，矩阵 H k \mathbf{H}k Hk 的多径分解估计是通过哈达玛积（ Hadamard product ）结合 r k \mathbf{r}k rk 和 T \mathbf{T} T 的第 i i i 行（记为 T i \mathbf{T}i Ti ）来获得的，即 X i , k = T i T ∘ r k \mathbf{X}{i,k} = \mathbf{T}i^{\text{T}} \circ \mathbf{r}k Xi,k=TiT∘rk 。最后， (8) 中的 H ^ i , k \hat{H}{i,k} H^i,k 通过 H ^ i , k = ∑ l = 1 L ′ X i , k , l X i , k , 0 ∗ \hat{H}{i,k} = \sum{l=1}^{L'} X{i,k,l} X{i,k,0}^* H^i,k=∑l=1L′Xi,k,lXi,k,0∗ 获得，其中 X i , k , 0 X_{i,k,0} Xi,k,0 是向量 X i , k \mathbf{X}_{i,k} Xi,k 的第一个元素，并且与最强的多径分量相关联。

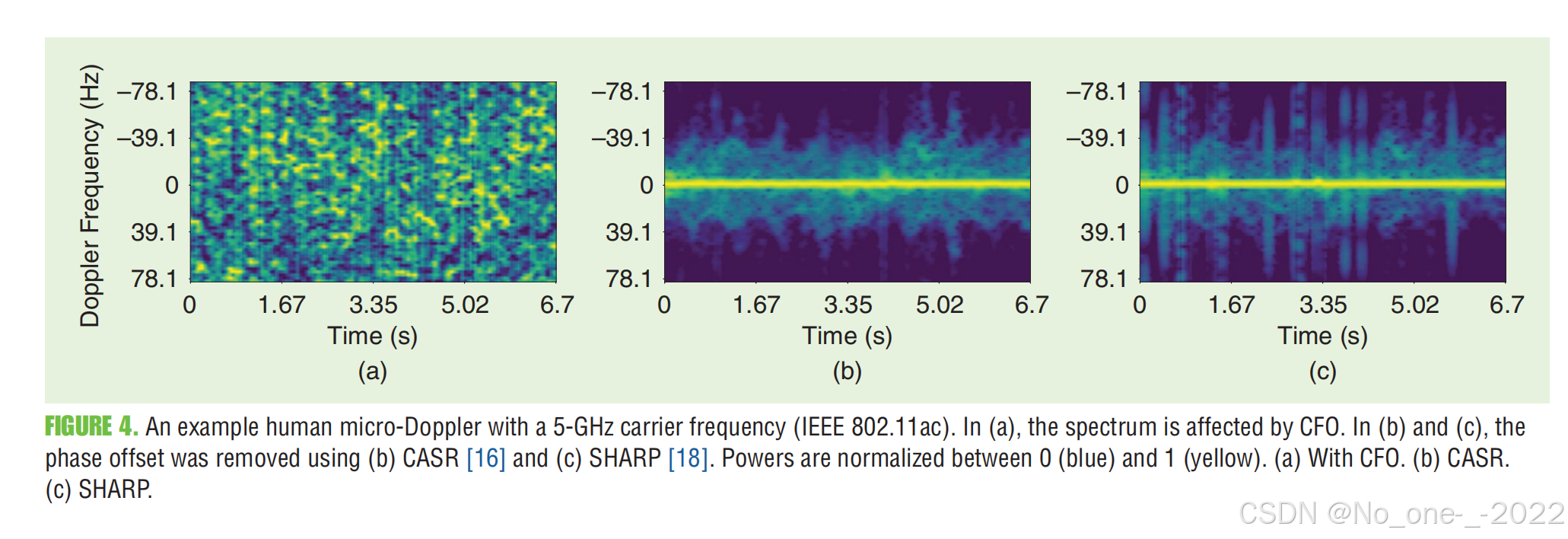
比较 CASR 和 SHARP 在人体微多普勒频谱图提取方面的示例结果如图 4 所示。这些结果基于具有 5-GHz 载波频率的 IEEE 802.11ac 测试平台。

Offset Estimation Methods

与前面提到的利用空域或时域特征来消除由时钟异步引起的随机相位偏移（即（2）式中的 ξ i , k \xi_{i,k} ξi,k ）的方法不同，文献 [19] 、 [20] 和 [21] 中的设计旨在估计并补偿偏移，以实现高性能的多普勒感知。其基本原理可以从（4）式中看出------如果分母中只保留静态路径，多普勒估计就不再受 CASR 引起的非线性的影响。

文献 [19] 和 [20] 采用空域线性组合（A spatial-domain linear combination）来抑制与动态路径相关的信号。此类设计的出发点是空域中的收发关系，正如（2）式中的导向矢量所包含的那样。更具体地说，其中的 H i , k \mathbf{H}{i,k} Hi,k 可以看作是 a ( N , ϕ l ) a T ( M , θ l ) \mathbf{a}(N, \phi_l)\mathbf{a}^{\text{T}}(M, \theta_l) a(N,ϕl)aT(M,θl) 的线性组合，它是关于发射和接收阵列的两个导向矢量的外积。这种外积主要传达了路径的空间信息。基于矩阵运算规则 vec ( A B C ) = C T ⊗ A vec ( B ) \text{vec}(\mathbf{A}\mathbf{B}\mathbf{C}) = \mathbf{C}^{\text{T}} \otimes \mathbf{A}\text{vec}(\mathbf{B}) vec(ABC)=CT⊗Avec(B) （其中 ⊗ \otimes ⊗ 表示克罗内克积），我们可以对 H i , k \mathbf{H}{i,k} Hi,k 进行向量化并得到

vec ( H i , k ) = [ a ( M , θ 1 ) ⊗ a ( N , ϕ 1 ) , ... , a ( M , θ L ) ⊗ a ( N , ϕ L ) ] ⏟ A b i , k (10) \text{vec}(\mathbf{H}{i,k}) = \underbrace{[\mathbf{a}(M, \theta_1) \otimes \mathbf{a}(N, \phi_1), \dots, \mathbf{a}(M, \theta_L) \otimes \mathbf{a}(N, \phi_L)]}{\mathbf{A}} \mathbf{b}_{i,k} \tag{10} vec(Hi,k)=A [a(M,θ1)⊗a(N,ϕ1),...,a(M,θL)⊗a(N,ϕL)]bi,k(10)

其中 b i , k \mathbf{b}_{i,k} bi,k 是一个列向量，收集了（2）式中 L L L 条路径的系数。上述转换类似于传统的 MIMO 雷达处理，其中 M M M 个发射天线和 N N N 个接收天线可以产生 M N MN MN 个虚拟天线。利用阵列信号处理理论，我们发现识别动态路径的零空间（the null space of dynamic paths）在理论上是可行的。将 CSI 信号投影到零空间，进而有助于估计与静态路径相关的信道系数。

• 为了实现这一点，文献 [19] 执行了一项优化，以寻找虚拟天线上的线性组合，该组合能够最小化呼吸能量与整体信号能量的比值。呼吸能量是由人体呼吸运动引起的频率范围内的信号能量，它可以根据系统配置（如载波频率和收发机的几何关系）来确定。

• 在文献 [20] 中， MUSIC 算法估计了静态和动态路径的 AoA 。该工作表明，在存在强 LoS 路径的情况下， Bartlett 波束成形器会在 LoS 路径处形成一个峰值。然后利用这一特征来区分 LoS 路径的 AoA 与动态路径的 AoA 。随后在空域中构造动态路径的零空间以提取 LoS 路径，这有助于估计由异步引起的复合随机相位 ξ i , k \xi_{i,k} ξi,k 。类似地，零空间方法通过抑制其他路径来提取每条动态路径，从而能够估计它们的多普勒频率。

• 如果存在强 LoS 路径，并且只关注多普勒信息，那么通过充分利用 LoS 路径来估计并补偿异步偏移可能会非常有效。这在文献 [21] 中得到了证明。通过将（1）式中的第一条路径视为强 LoS 路径，那么 b 1 e − j 2 π i ( τ 1 + τ o , k ) Δ f b_1 e^{-j2\pi i(\tau_1+\tau_{o,k})\Delta_f} b1e−j2πi(τ1+τo,k)Δf 可以被视为由子载波索引 i i i 索引的单音信号。估计该信号的频率可以为我们提供 LoS 路径延迟加上 TO 的复合延迟的估计值。我们建议感兴趣的读者参考文献 [21] 和 [26] 以了解估计方法的细节。它基于离散傅里叶变换（ DFT ）插值，这是一种流行的、具有离网格精度的低复杂度频率估计方法。在估计出 LoS 路径的复合延迟（即 τ 1 + τ o , k \tau_1 + \tau_{o,k} τ1+τo,k ）之后，信号可以在 LoS 路径上相干累积，并且高信噪比（ SNR ）累积信号的相位可以用作所有其他随机相位偏移的估计值。这种方法适用于（1）式中所示的任何天线和符号。

Comparisons and Remarks

表 1 比较了前面回顾的所有方法的要求和特征，其中 OTA 代表"空口（ over the air ）"。这三种类型在"基于单节点的双基感知技术"一节的开头有所阐述，其中第一种类型进一步分为两个子类型：

• 表中的类型 I(S) 下的空域方法在"偏移抵消方法：空域处理"一节中进行了回顾；
• 而类型 I(D) 下的时延域方法在"偏移抵消方法：时延域处理技术"一节中进行了回顾。

在表 1 中，这三个域主要指的是处理偏移所在的位置。如前所述，大多数工作主要在空域中进行。然而，最近的一些工作结合了其他域，以减轻对多天线的依赖，并探索可用的自由度。

此外，并非所有方法都能感知环境中同时移动的多个目标。

• 具体而言， CACC 和时延域技术支持多个目标，前提是具有足够的带宽和 / 或 AoA 分辨率来分辨相应的多径分量。
• 相反（Conversely）， CASR 主要适用于单目标场景，并且需要特殊的处理来分离多个目标的贡献，如文献 [17] 和 [19] 所示。

作为一项与感知相关的应用， 5G 及未来网络中的定位正在成为一个热门的研究课题 [28], [29] 。在这类应用中， TO 备受关注，因为到达时间通常是定位算法中使用的一个关键感知参数。

• 在文献 [28] 中，提出了到达时间差来抵消 TO 。在
• 文献 [29] 中，开发了一种新颖的最大似然估计器来估计 TO 以及诸如多径角度等其他感知参数。

虽然可以使用这些方法来估计 TO ，但它们没有充分处理频率偏移和随机相位。在双基感知中，"偏移抵消方法：时延域处理技术"、"偏移估计方法"和"混合方法"小节中回顾的方法可以在这些方法 [28], [29] 的基础上进一步应用；或者，将文献 [28], [29] 的方法进行扩展以考虑另外两种类型的偏移，这也将是非常有意义的。

我们需要说明的是，本节回顾的方法背后的思想有望在 6G 背景下用于解决时钟偏移问题，尽管其中相当一部分是在 Wi-Fi 感知背景下开发出来的。这是因为，无论网络差异如何，蜂窝网络和 Wi-Fi 网络都使用了 MIMO-OFDM 波形，并且所有被回顾的方法都可以应用于通用的 MIMO-OFDM 设置。然而，值得注意的是，在将这些方法应用于 6G 网络时，由于 6G 网络与 Wi-Fi 相比可能具有不同的特征，因此可能需要进行调整 / 改变，如下文所强调的那样。

• 6G 基站可能会配备所谓的大规模 MIMO 阵列，这可以被有效地用于实现高空间分辨率并分离要感知的多个物体。毫米波（ mmWave ）系统可能在数字波束赋形之前采用模拟波束赋形的混合阵列。这意味着跨天线技术 [12], [13], [14], [15], [16], [17] 将需要进行扩展以处理跨波束信号（cross-beam signals）。此外，可以通过设计模拟波束赋形来促进更好地解决时钟偏移的方案。

  "跨波束信号"就是指在混合阵列架构下，基带算法的操作对象从"物理天线端口的信号"变成了"射频模拟合成波束端口的信号"。这其实与处理混合架构 DOA 估计时的逻辑本质是一致的：接收信号模型中存在的那个模拟波束赋形矩阵，彻底改变了基带对空间信号的观测维度，因此算法必须随之升级。

• 预计 6G 将具有比 Wi-Fi 更大的频率带宽，从而在时频域资源中带来更多的自由度。这可以进一步改进本节回顾的一些方法。例如， SHARP [18] 可以利用大带宽来在距离域实现高得多的分辨率，从而更有效地解决时钟偏移问题。另一个例子是，可以像文献 [24] 中那样，求助于时频域中的波形设计，以获得更好的偏移估计性能。

• 6G 网络可能在室内和室外都有部署。对于室内应用，信道将类似于 Wi-Fi 信道，在 Wi-Fi 平台上验证过的技术有望在 6G 网络上有效发挥作用。 6G 室外信道可能与 Wi-Fi 信道有很大不同。这使得依赖于信道的方法（例如室内 Wi-Fi 场景下的文献 [19] ）无法直接应用于 6G 。然而，这种思路是可以借鉴的。例如，在 6G 室外感知中，可以不使用呼吸运动来估计跨天线的最佳组合（更多细节请参见"偏移估计方法"一节），而是利用由农村地区汽车运动引起的时变信道来实现类似的目标。

Future Research Directions and Open Problems

我们已经在解决双基 ISAC 中的时钟异步问题上看到了充满前景的进展。然而，无可否认的是，许多开放性问题仍然需要学术界和工业界的更多关注。

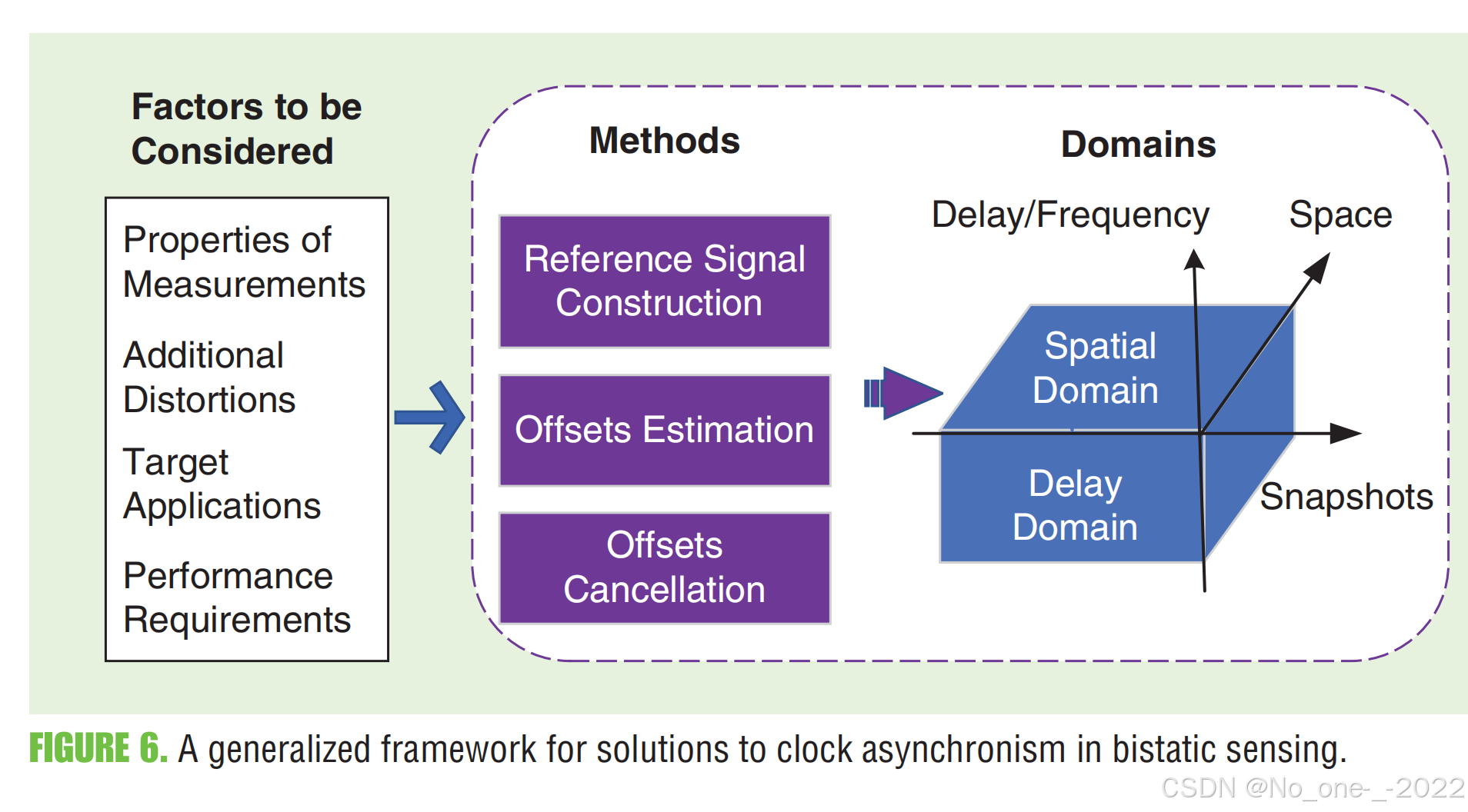
先前关于这些技术的讨论使我们能够建立一个综合框架，为在更高层面上（at an elevated level）进行未来研究奠定基础。如图 6 所示，该框架是二维（2D）的。

1. 一个维度涵盖了信号处理方法，包括参考信号构造、偏移估计以及通过互相关和信号比值进行的偏移抵消（offset cancellation via the cross-correlation and signal ratio）。

2. 第二个维度涉及主要应用信号处理的域，即典型的空域和时延域。这些方法具有灵活性，可以单独实施，也可以在一个或多个域中组合实施（in combination across one or more domains）。
   

尽管在"基于单节点的双基感知技术"一节中探讨的现有工作已经证实了其可行性并展现了潜力，但对这些方法及其应用领域的优缺点进行全面审视后，我们发现其中仍蕴含着进一步完善与探索的契机。上述审视的总结如下：

• 构造参考信号可以简化后续的感知参数估计，但不可避免地会引入误差。

• 偏移估计能够实现灵活的信号处理。然而，它也面临估计误差，这些误差可能比参考信号构造中的误差更大。

• 偏移抵消利用信号结构并在不引入误差的情况下消除偏移。然而，它通常会导致需要估计更多的参数（如信号互相关）或产生非线性问题（如信号比值）。

• 空域处理很好地保持了路径在时延域和多普勒域中的独立性，但需要多条接收链路（multiple receiving chains are required），这可能不具备成本效益，特别是对于毫米波（mmWave）系统而言。

• 时延域处理只需要一根接收天线，但在 OFDM 系统中，当仅在部分子载波上可获得测量值时，获取信道冲激响应（CIR）有时具有挑战性。此外，当时延偏离网格（off grid）时，每个 CIR 可能是多条路径的叠加。

因此，通过联合考虑这些方法和域各自的优缺点，以及额外的信号和系统因素（如图 6 所示），可以设计出一种合适的组合。通过清晰勾勒信号处理方法及其应用领域的二维全景（By delineating the 2D landscape of signal processing methods and their application domains），有望催生出新颖的算法组合与创新突破。在这一框架下，接下来我们将详细探讨一些更为具体的研究问题。

Construction of a Reference Path

高效可靠地构造参考路径是时延域处理技术中一个有趣且开放的研究挑战，以实现相位偏移补偿。文献 [22] 提出应用跟踪算法来维持对几条候选参考路径的估计，包括静态物体上的一阶反射。然而，感知精度取决于从参考路径接收到的信号质量，并且会随着低信噪比（ SNR ）而下降。

Sensing of Multiple Targets

据我们所知，只有两项工作（ [19] 和 [22] ）在环境中存在多个并发移动的感知目标所收集的数据上，通过实验验证了相位偏移消除技术（分别是混合方法、时延域方法和 CASR ）。在这种情况下，跨天线技术无法直接使用，并且需要分离不同主体贡献的技术，如"跨天线信号比值"一节所述。基于参考路径的技术不受多目标的影响。然而，当多个目标移动，可能导致视距（ LoS ）遮挡时，获取可靠的参考路径极具挑战性，值得研究界的进一步关注。

Mobility of the Nodes

在存在相位偏移的情况下，使用移动节点执行 ISAC 是一个具有挑战性的问题。值得注意的是，发送端（ Tx ）和接收端（ Rx ）静止的假设对于所有三种相位偏移消除技术都至关重要。据我们所知，只有文献 [30] 提出了一个用于 Wi-Fi 感知的初步动态 CFR 模型，但它没有处理相位偏移问题。解决这个问题的可能方法也许来自无源雷达领域的文献，在这些文献中，安装在移动平台上的雷达得到了充分的研究，例如文献 [31] 。

Coherently Combine Multiple Rxs

为了充分发挥无处不在的 ISAC 的潜力，需要开发出结合来自多个相位同步的 Rx 的信息的算法。这将提高系统的感知分辨率，克服带宽带来的限制，并实现波长级的感知精度。为了实现这一点，必须研究能够有效消除每个 Tx-Rx 之间不同相位偏移的算法，以允许对每个 Rx 处获得的数据进行相干融合。关于该主题的初步研究可以在文献 [32] 中找到。

Joint Spatial-Delay-Frequency-Domain Processing

从表 1 中我们可以看到，现有的设计通常利用三个域（空域、时延域和频域）中的一个或两个来解决时钟异步问题，而不是全部三个。这导致了现有方法的限制，例如，具有强 LoS 、大带宽或单条动态路径，这些通常与我们用于相位偏移补偿的域有关。例如，许多空域和频域方法需要强 LoS ，这对于时延域方法是不必要的。然而，时延域方法的性能可能受可用带宽的影响，而其他域则不然。联合使用这三个域可以让我们利用和结合不同方法的优势，有望消除大多数现有工作所受到的限制。

Open Dataset for Bistatic Sensing Research and Development

虽然在"基于单节点的双基感知技术"一节中回顾的大多数工作都进行了空口（ OTA ）实验以验证他们的方法，但自定义配置和硬件平台往往是异构的（custom configurations and hardware platforms are often heterogeneous），并且不遵循统一的标准。出于这个原因，只有少数公开可用的开源数据集（例如表 1 中提到的那些）是可用的。

在计算机和通信领域，"异构"指的就是缺乏统一的标准。大家都各自为战，使用的设备、参数、环境完全不一样，导致彼此之间的数据无法直接互通或对比。

此外，现有的大多数工作和实验都是基于 Wi-Fi 协议或平台的。其他无线系统（如移动网络）仅在少数工作中得到了验证，例如文献 [9] 。因此，进一步推进双基感知的一个关键方面是获取基于不同通信协议、在各种典型感知场景下收集的全面开源数据集，这些数据集可用于评估和比较所提出方法的性能。