文章目录
混叠频率公式
- 对于任意真实频率 f 0 f_0 f0,在采样频率 f s f_s fs 下产生的别名频率为:
f a = ∣ f 0 − f s ⋅ round ( f 0 f s ) ∣ \boxed{ f_a = \left| f_0 - f_s \cdot \operatorname{round}\left( \frac{f_0}{f_s} \right) \right| } fa= f0−fs⋅round(fsf0)
- 或等价地:
f a = ∣ ( f 0 + f s 2 ) m o d f s − f s 2 ∣ \boxed{ f_a = \left| \left( f_0 + \frac{f_s}{2} \right) \bmod f_s - \frac{f_s}{2} \right| } fa= (f0+2fs)modfs−2fs
-
其中 f a ∈ [ 0 , f s / 2 ] f_a \in [0, f_s/2] fa∈[0,fs/2]。
-
总结 :混叠不是"错误",而是采样过程在频域的自然表现;公式本质是将频率对 f s f_s fs 取模后折叠到奈奎斯特区间。避免混叠的关键是采样前低通滤波 ,确保 f max < f s / 2 f_{\max} < f_s/2 fmax<fs/2。
证明
- 频率混叠(aliasing)公式的证明可以从采样过程的频域分析 出发,利用傅里叶变换 和周期延拓的性质。
前提假设
- 原始连续时间信号为 x ( t ) x(t) x(t),其傅里叶变换为 X ( f ) X(f) X(f)。
- 信号是带限 的: X ( f ) = 0 X(f) = 0 X(f)=0 当 ∣ f ∣ > f max |f| > f_{\max} ∣f∣>fmax。
- 对 x ( t ) x(t) x(t) 以采样频率 f s f_s fs(采样间隔 T = 1 / f s T = 1/f_s T=1/fs)进行理想采样,得到离散序列:
x s ( t ) = x ( t ) ⋅ ∑ n = − ∞ ∞ δ ( t − n T ) x_s(t) = x(t) \cdot \sum_{n=-\infty}^{\infty} \delta(t - nT) xs(t)=x(t)⋅n=−∞∑∞δ(t−nT)
采样信号的频谱
- 根据傅里叶变换的时域相乘 ⇔ 频域卷积性质:
F { x s ( t ) } = X s ( f ) = X ( f ) ∗ F { ∑ n = − ∞ ∞ δ ( t − n T ) } \mathcal{F}\{x_s(t)\} = X_s(f) = X(f) * \mathcal{F}\left\{ \sum_{n=-\infty}^{\infty} \delta(t - nT) \right\} F{xs(t)}=Xs(f)=X(f)∗F{n=−∞∑∞δ(t−nT)}
- 而冲激串的傅里叶变换是另一个冲激串:
F { ∑ n = − ∞ ∞ δ ( t − n T ) } = f s ∑ k = − ∞ ∞ δ ( f − k f s ) \mathcal{F}\left\{ \sum_{n=-\infty}^{\infty} \delta(t - nT) \right\} = f_s \sum_{k=-\infty}^{\infty} \delta(f - k f_s) F{n=−∞∑∞δ(t−nT)}=fsk=−∞∑∞δ(f−kfs)
- 因此,
X s ( f ) = X ( f ) ∗ [ f s ∑ k = − ∞ ∞ δ ( f − k f s ) ] = f s ∑ k = − ∞ ∞ X ( f − k f s ) X_s(f) = X(f) * \left[ f_s \sum_{k=-\infty}^{\infty} \delta(f - k f_s) \right] = f_s \sum_{k=-\infty}^{\infty} X(f - k f_s) Xs(f)=X(f)∗[fsk=−∞∑∞δ(f−kfs)]=fsk=−∞∑∞X(f−kfs)
关键结论 :采样后的频谱是原始频谱以 f s f_s fs 为周期,在频域无限重复(周期延拓,且偶次奈奎斯特频带是奇次奈奎斯特频带的镜像)。
混叠的发生条件
- 若 f s > 2 f max f_s > 2 f_{\max} fs>2fmax,则各副本 X ( f − k f s ) X(f - k f_s) X(f−kfs) 之间不重叠 ,可通过理想低通滤波器(截止频率 f s / 2 f_s/2 fs/2)完全恢复 X ( f ) X(f) X(f)。
- 若 f s ≤ 2 f max f_s \leq 2 f_{\max} fs≤2fmax,则相邻频谱副本相互重叠 ,导致高频成分"折叠"到低频区域------这就是混叠。
混叠频率(Aliased Frequency)的推导
- 考虑一个单一频率的正弦信号:
x ( t ) = cos ( 2 π f 0 t ) x(t) = \cos(2\pi f_0 t) x(t)=cos(2πf0t)
-
采样后,频谱变为:
X s ( f ) = f s 2 ∑ k = − ∞ ∞ [ δ ( f − f 0 − k f s ) + δ ( f + f 0 − k f s ) ] X_s(f) = \frac{f_s}{2} \sum_{k=-\infty}^{\infty} \left[ \delta(f - f_0 - k f_s) + \delta(f + f_0 - k f_s) \right] Xs(f)=2fsk=−∞∑∞[δ(f−f0−kfs)+δ(f+f0−kfs)]
- 这意味着在频域中,所有频率点形如:
f = ± f 0 + k f s , k ∈ Z f = \pm f_0 + k f_s, \quad k \in \mathbb{Z} f=±f0+kfs,k∈Z
-
当我们用数字系统(如DFT或人耳)观察这个离散信号时,只能感知到主频带 [ − f s 2 , f s 2 ] [-\frac{f_s}{2}, \frac{f_s}{2}] [−2fs,2fs] 内的频率(因为这是奈奎斯特区间)。
-
因此,真实频率 f 0 f_0 f0 在采样后会被"映射"到该区间内的某个等效频率 f a f_a fa,满足:
f a ≡ f 0 ( m o d f s ) 且 f a ∈ [ − f s 2 , f s 2 ] f_a \equiv f_0 \pmod{f_s} \quad \text{且} \quad f_a \in \left[ -\frac{f_s}{2}, \frac{f_s}{2} \right] fa≡f0(modfs)且fa∈[−2fs,2fs]
- 通常我们关心非负频率 ,所以取绝对值并限制在 [ 0 , f s / 2 ] [0, f_s/2] [0,fs/2]:
f a = min k ∈ Z ∣ f 0 − k f s ∣ f_a = \min_{k \in \mathbb{Z}} \left| f_0 - k f_s \right| fa=k∈Zmin∣f0−kfs∣
-
这等价于将 f 0 f_0 f0 对 f s f_s fs 取模后,再"折叠"到奈奎斯特区间。
-
更明确地,定义:
f a = ∣ ( ( f 0 + f s 2 ) m o d f s ) − f s 2 ∣ f_a = \left| \left( (f_0 + \tfrac{f_s}{2}) \bmod f_s \right) - \tfrac{f_s}{2} \right| fa= ((f0+2fs)modfs)−2fs
- 即混频频率公式。
例子
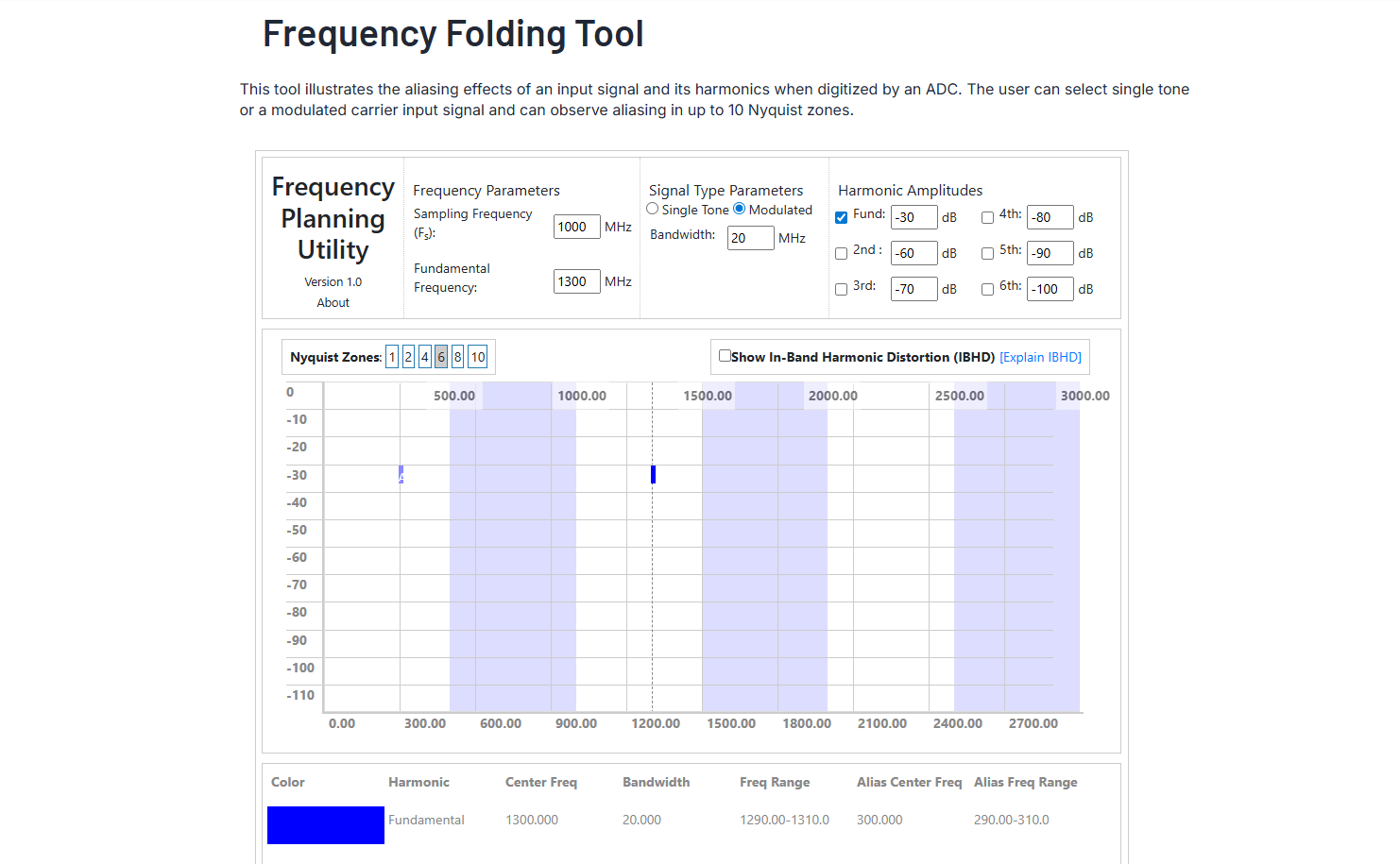
设 f s = 1000 Hz f_s = 1000\,\text{Hz} fs=1000Hz, f 0 = 1300 Hz f_0 = 1300\,\text{Hz} f0=1300Hz
-
f 0 > f s / 2 = 500 Hz f_0 > f_s/2 = 500\,\text{Hz} f0>fs/2=500Hz → 必然混叠
-
计算: f a = ∣ 1300 − 1 × 1000 ∣ = 300 Hz f_a = |1300 - 1 \times 1000| = 300\,\text{Hz} fa=∣1300−1×1000∣=300Hz
-
或用模运算:
( 1300 + 500 ) m o d 1000 = 1800 m o d 1000 = 800 (1300 + 500) \bmod 1000 = 1800 \bmod 1000 = 800 (1300+500)mod1000=1800mod1000=800
800 − 500 = 300 Hz 800 - 500 = 300\,\text{Hz} 800−500=300Hz -
采样后的离散信号与 300 Hz 正弦波完全无法区分。
通过采样做频谱搬移/带通采样(Bandpass Sampling)实现频谱搬移
- 通过采样实现频谱搬移 (Spectral Shifting)是一种在数字信号处理和通信系统中常用的技术,其核心思想是:利用采样过程中的频谱周期延拓特性,将信号的频谱"搬移"到新的频率位置 。这不同于传统用混频器(乘以载波)实现的频谱搬移,而是通过欠采样(undersampling)或带通采样(bandpass sampling) 来实现。
采样导致频谱周期延拓
对一个连续时间信号 x ( t ) x(t) x(t) 以采样频率 f s f_s fs 采样后,其频谱变为:
X s ( f ) = f s ∑ k = − ∞ ∞ X ( f − k f s ) X_s(f) = f_s \sum_{k=-\infty}^{\infty} X(f - k f_s) Xs(f)=fsk=−∞∑∞X(f−kfs)
即原始频谱以 f s f_s fs 为周期,在频域无限重复。
关键点 :如果原始信号是带通信号 (能量集中在某个高频段,如 f L ∼ f H f_L \sim f_H fL∼fH),且我们故意让 f s < 2 f H f_s < 2f_H fs<2fH (即违反低通信号的奈奎斯特条件),但精心选择 f s f_s fs,使得某个频谱副本恰好落在基带 (0 附近)或目标频段,就实现了无混叠的频谱搬移。
适用场景
- 信号是带限带通信号 ,中心频率 f c f_c fc,带宽 B = f H − f L B = f_H - f_L B=fH−fL。
- 不想使用模拟混频器下变频,而是直接用ADC采样,同时完成下变频 + 数字化。
- 这是一种巧妙利用采样定理边界条件的工程技巧,体现了"混叠"在特定场景下的正面价值。
带通采样定理
- 若信号频带位于 [ f L , f H ] [f_L, f_H] [fL,fH],带宽 B = f H − f L B = f_H - f_L B=fH−fL,则存在采样频率 f s f_s fs 满足:
2 f H n ≤ f s ≤ 2 f L n − 1 \frac{2f_H}{n} \leq f_s \leq \frac{2f_L}{n-1} n2fH≤fs≤n−12fL
- 其中 n = ⌊ f H B ⌋ n = \left\lfloor \frac{f_H}{B} \right\rfloor n=⌊BfH⌋(或取满足不等式的整数)。此时,采样后的频谱副本之一会完整地落入 [ 0 , f s / 2 ] [0, f_s/2] [0,fs/2] 区间,且无混叠。
频谱搬移效果
- 原始信号中心频率 f c f_c fc 被"搬移"到数字基带中的某个频率 f_a 。
- 这个 f a f_a fa 就是别名频率,由混叠公式给出:
f a = ∣ f c − k f s ∣ (选择 k 使 f a ∈ [ 0 , f s / 2 ] ) f_a = |f_c - k f_s| \quad \text{(选择 } k \text{ 使 } f_a \in [0, f_s/2] \text{)} fa=∣fc−kfs∣(选择 k 使 fa∈[0,fs/2])
- 这就是通过采样实现的频谱搬移:高频信号被"折叠"到低频,无需模拟混频。
例子
假设有一个射频信号:
-
频带: f L = 98 MHz , f H = 102 MHz f_L = 98\,\text{MHz},\ f_H = 102\,\text{MHz} fL=98MHz, fH=102MHz → 带宽 B = 4 MHz B = 4\,\text{MHz} B=4MHz
-
中心频率 f c = 100 MHz f_c = 100\,\text{MHz} fc=100MHz
-
按传统奈奎斯特采样(低通观点),需 f s > 204 MHz f_s > 204\,\text{MHz} fs>204MHz,对ADC要求高。
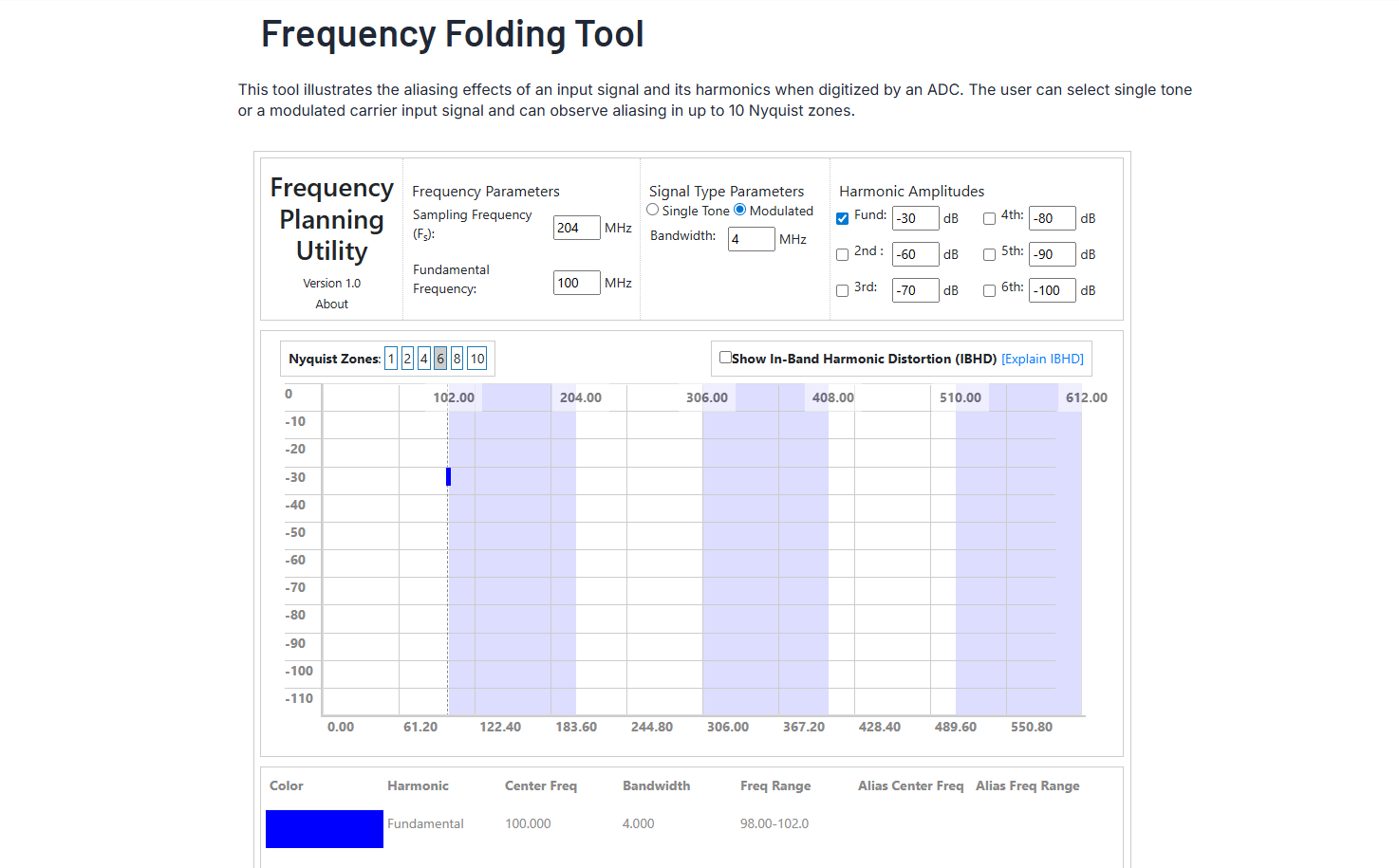
但采用带通采样:
- 取 n = ⌊ 102 4 ⌋ = 25 n = \left\lfloor \frac{102}{4} \right\rfloor = 25 n=⌊4102⌋=25
- 计算允许的 f s f_s fs 范围:
2 × 102 25 = 8.16 MHz ≤ f s ≤ 2 × 98 24 ≈ 8.17 MHz \frac{2 \times 102}{25} = 8.16\,\text{MHz} \leq f_s \leq \frac{2 \times 98}{24} \approx 8.17\,\text{MHz} 252×102=8.16MHz≤fs≤242×98≈8.17MHz
→ 可选 f s = 8.165 MHz f_s = 8.165\,\text{MHz} fs=8.165MHz
采样后,100 MHz 的信号会混叠到:
f a = ∣ 100 − 12 × 8.165 ∣ ≈ ∣ 100 − 97.98 ∣ = 2.02 MHz f_a = |100 - 12 \times 8.165| \approx |100 - 97.98| = 2.02\,\text{MHz} fa=∣100−12×8.165∣≈∣100−97.98∣=2.02MHz
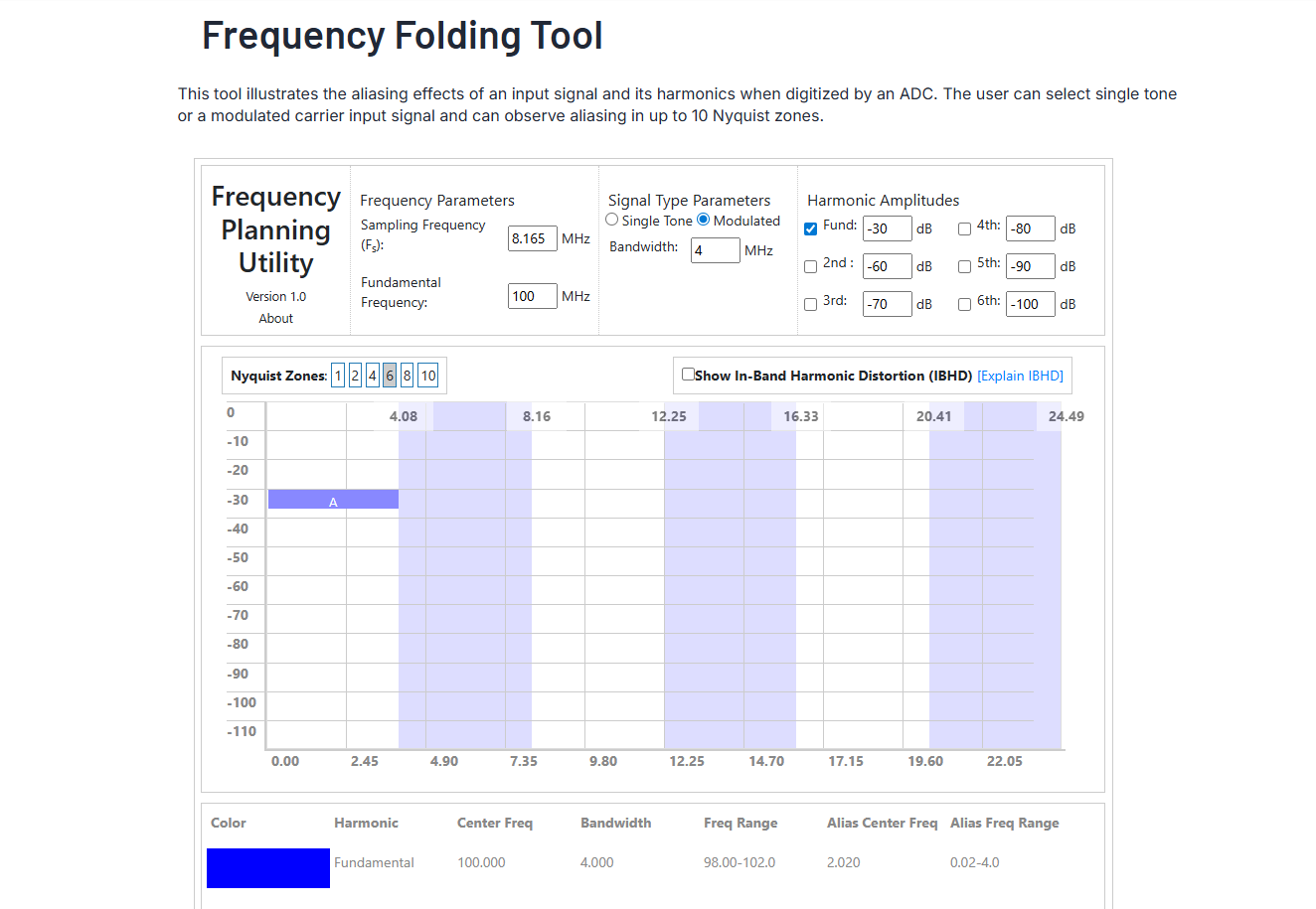
- 结果:100 MHz 的信号被直接采样并搬移到 2.02 MHz 的数字基带,后续可用数字信号处理(如数字下变频)进一步处理。
总结
| 方法 | 实现方式 | 硬件复杂度 | 频谱搬移原理 |
|---|---|---|---|
| 模拟混频 | 乘以本地振荡器(LO) | 需混频器、滤波器、LO | 频域卷积(平移) |
| 采样搬移 | 直接高速ADC采样 | 仅需ADC + 带通滤波器 | 频谱周期延拓 + 混叠 |
在软件定义无线电(SDR)、雷达、5G 射频采样等系统中,带通采样实现频谱搬移被广泛应用,可简化前端架构。
- 抗混叠滤波器必须是带通型 :只允许 [ f L , f H ] [f_L, f_H] [fL,fH] 通过,阻止其他频段干扰。
- 采样时钟抖动影响更大:高频信号对采样精度更敏感。
- 并非所有 f s f_s fs 都可行:必须严格满足带通采样不等式,否则频谱重叠。
- 仅适用于窄带信号 :带宽 B ≪ f c B \ll f_c B≪fc 时最有效。
通过采样做频谱搬移的本质是:利用欠采样(带通采样)有意引入"可控混叠",使高频信号的频谱副本落入基带,从而在数字化的同时完成下变频。
关键公式:
- 搬移后频率: f a = ∣ f c − k f s ∣ ∈ [ 0 , f s / 2 ] f_a = |f_c - k f_s| \in [0, f_s/2] fa=∣fc−kfs∣∈[0,fs/2]
- 采样率选择:满足 2 f H n ≤ f s ≤ 2 f L n − 1 \frac{2f_H}{n} \leq f_s \leq \frac{2f_L}{n-1} n2fH≤fs≤n−12fL