【习题解答】轨道力学-第1章-质点动力学

第1章 质点动力学 习题

1.1 已知三个矢量 A=Axi^+Ayj^+Azk^\mathbf{A} = A_{x}\hat{\pmb{i}} + A_{y}\hat{\pmb{j}} + A_{z}\hat{\pmb{k}}A=Axi^+Ayj^+Azk^ ， B=Bxi^+Byj^+Bzk^\mathbf{B} = B_{x}\hat{\pmb{i}} + B_{y}\hat{\pmb{j}} + B_{z}\hat{\pmb{k}}B=Bxi^+Byj^+Bzk^ ， C=Cxi^+Cyj^+Czk^\mathbf{C} = C_{x}\hat{\pmb{i}} + C_{y}\hat{\pmb{j}} + C_{z}\hat{\pmb{k}}C=Cxi^+Cyj^+Czk^ 分析并证明如下结论：

(1) A⋅A=A2\mathbf{A} \cdot \mathbf{A} = A^{2}A⋅A=A2 ;

(2) A⋅(B×C)=(A×B)⋅C\mathbf{A} \cdot (\mathbf{B} \times \mathbf{C}) = (\mathbf{A} \times \mathbf{B}) \cdot \mathbf{C}A⋅(B×C)=(A×B)⋅C （点乘和叉乘的交换律）；

(3) A×(B×C)=B(A⋅C)−C(A⋅B)\mathbf{A} \times (\mathbf{B} \times \mathbf{C}) = \mathbf{B}(\mathbf{A} \cdot \mathbf{C}) - \mathbf{C}(\mathbf{A} \cdot \mathbf{B})A×(B×C)=B(A⋅C)−C(A⋅B) （bac-cab法则）。

只需分别计算出等号两边的表达式并计算其相等，不需代入具体数值。计算过程中要用到笛卡儿坐标系中单位矢量的性质。

i^⋅j^=i^⋅k^=j^⋅k^=0,i^⋅i^=j^⋅j^=k^⋅k^=1 \hat {\boldsymbol {i}} \cdot \hat {\boldsymbol {j}} = \hat {\boldsymbol {i}} \cdot \hat {\boldsymbol {k}} = \hat {\boldsymbol {j}} \cdot \hat {\boldsymbol {k}} = 0, \quad \hat {\boldsymbol {i}} \cdot \hat {\boldsymbol {i}} = \hat {\boldsymbol {j}} \cdot \hat {\boldsymbol {j}} = \hat {\boldsymbol {k}} \cdot \hat {\boldsymbol {k}} = 1 i^⋅j^=i^⋅k^=j^⋅k^=0,i^⋅i^=j^⋅j^=k^⋅k^=1

i^×j^=k^,j^×k^=i^,k^×i^=j^(i^×k^=−j^,j^×i^=−k^,k^×j^=−i^) \hat {\boldsymbol {i}} \times \hat {\boldsymbol {j}} = \hat {\boldsymbol {k}}, \quad \hat {\boldsymbol {j}} \times \hat {\boldsymbol {k}} = \hat {\boldsymbol {i}}, \hat {\boldsymbol {k}} \times \hat {\boldsymbol {i}} = \hat {\boldsymbol {j}} (\hat {\boldsymbol {i}} \times \hat {\boldsymbol {k}} = - \hat {\boldsymbol {j}}, \hat {\boldsymbol {j}} \times \hat {\boldsymbol {i}} = - \hat {\boldsymbol {k}}, \hat {\boldsymbol {k}} \times \hat {\boldsymbol {j}} = - \hat {\boldsymbol {i}}) i^×j^=k^,j^×k^=i^,k^×i^=j^(i^×k^=−j^,j^×i^=−k^,k^×j^=−i^)

i^×i^=j^×j^=k^×k^=0 \hat {\boldsymbol {i}} \times \hat {\boldsymbol {i}} = \hat {\boldsymbol {j}} \times \hat {\boldsymbol {j}} = \hat {\boldsymbol {k}} \times \hat {\boldsymbol {k}} = \mathbf {0} i^×i^=j^×j^=k^×k^=0

解答与解析：

证明：

(1) A⋅A=AxAx+AyAy+AzAz=Ax2+Ay2+Az2=∣A∣2=A2\mathbf{A} \cdot \mathbf{A} = A_x A_x + A_y A_y + A_z A_z = A_x^2 + A_y^2 + A_z^2 = |\mathbf{A}|^2 = A^2A⋅A=AxAx+AyAy+AzAz=Ax2+Ay2+Az2=∣A∣2=A2。

(2) 标量三重积 A⋅(B×C)\mathbf{A} \cdot (\mathbf{B} \times \mathbf{C})A⋅(B×C) 表示由 A,B,C\mathbf{A}, \mathbf{B}, \mathbf{C}A,B,C 构成的平行六面体的体积。其满足循环移位性质：

A⋅(B×C)=B⋅(C×A)=C⋅(A×B)\mathbf{A} \cdot (\mathbf{B} \times \mathbf{C}) = \mathbf{B} \cdot (\mathbf{C} \times \mathbf{A}) = \mathbf{C} \cdot (\mathbf{A} \times \mathbf{B})A⋅(B×C)=B⋅(C×A)=C⋅(A×B)

利用点乘交换律 C⋅(A×B)=(A×B)⋅C\mathbf{C} \cdot (\mathbf{A} \times \mathbf{B}) = (\mathbf{A} \times \mathbf{B}) \cdot \mathbf{C}C⋅(A×B)=(A×B)⋅C，得证。

(3) 向量三重积公式 (bac-cab rule)：

A×(B×C)=B(A⋅C)−C(A⋅B)\mathbf{A} \times (\mathbf{B} \times \mathbf{C}) = \mathbf{B}(\mathbf{A} \cdot \mathbf{C}) - \mathbf{C}(\mathbf{A} \cdot \mathbf{B})A×(B×C)=B(A⋅C)−C(A⋅B)

可通过展开分量证明（略）。

---

1.2 利用上题中(1)、(2)两式的矢量性质，证明

(A×B)⋅(C×D)=(A⋅C)(B⋅D)−(A⋅D)(B⋅C) (\mathbf {A} \times \mathbf {B}) \cdot (\mathbf {C} \times \mathbf {D}) = (\mathbf {A} \cdot \mathbf {C}) (\mathbf {B} \cdot \mathbf {D}) - (\mathbf {A} \cdot \mathbf {D}) (\mathbf {B} \cdot \mathbf {C}) (A×B)⋅(C×D)=(A⋅C)(B⋅D)−(A⋅D)(B⋅C)

解答与解析：

利用 P⋅(Q×R)=(P×Q)⋅R\mathbf{P} \cdot (\mathbf{Q} \times \mathbf{R}) = (\mathbf{P} \times \mathbf{Q}) \cdot \mathbf{R}P⋅(Q×R)=(P×Q)⋅R。

令 P=A×B\mathbf{P} = \mathbf{A} \times \mathbf{B}P=A×B，则左式 =(A×B)⋅(C×D)= (\mathbf{A} \times \mathbf{B}) \cdot (\mathbf{C} \times \mathbf{D})=(A×B)⋅(C×D)。

将其看作点乘：U⋅(C×D)=(U×C)⋅D\mathbf{U} \cdot (\mathbf{C} \times \mathbf{D}) = (\mathbf{U} \times \mathbf{C}) \cdot \mathbf{D}U⋅(C×D)=(U×C)⋅D？不，这里用拉格朗日恒等式更直接，或者利用向量代数性质。

我们可以将 (C×D)(\mathbf{C} \times \mathbf{D})(C×D) 看作一个整体矢量 V\mathbf{V}V。

原式 =(A×B)⋅V=A⋅(B×V)=A⋅[B×(C×D)]= (\mathbf{A} \times \mathbf{B}) \cdot \mathbf{V} = \mathbf{A} \cdot (\mathbf{B} \times \mathbf{V}) = \mathbf{A} \cdot [\mathbf{B} \times (\mathbf{C} \times \mathbf{D})]=(A×B)⋅V=A⋅(B×V)=A⋅[B×(C×D)].

利用 bac-cab 法则：B×(C×D)=C(B⋅D)−D(B⋅C)\mathbf{B} \times (\mathbf{C} \times \mathbf{D}) = \mathbf{C}(\mathbf{B} \cdot \mathbf{D}) - \mathbf{D}(\mathbf{B} \cdot \mathbf{C})B×(C×D)=C(B⋅D)−D(B⋅C)。

代入得：A⋅[C(B⋅D)−D(B⋅C)]=(A⋅C)(B⋅D)−(A⋅D)(B⋅C)\mathbf{A} \cdot [\mathbf{C}(\mathbf{B} \cdot \mathbf{D}) - \mathbf{D}(\mathbf{B} \cdot \mathbf{C})] = (\mathbf{A} \cdot \mathbf{C})(\mathbf{B} \cdot \mathbf{D}) - (\mathbf{A} \cdot \mathbf{D})(\mathbf{B} \cdot \mathbf{C})A⋅[C(B⋅D)−D(B⋅C)]=(A⋅C)(B⋅D)−(A⋅D)(B⋅C)。

得证。

---

1.3 如图P.1.3所示， OOO 点的绝对位置、速度和加速度分别为

rO=300I^+200J^+100K^(m) \boldsymbol {r} _ {O} = 3 0 0 \hat {\boldsymbol {I}} + 2 0 0 \hat {\boldsymbol {J}} + 1 0 0 \hat {\boldsymbol {K}} (\mathrm {m}) rO=300I^+200J^+100K^(m)

vO=−10I^+30J^−50K^(m/s) \boldsymbol {v} _ {O} = - 1 0 \hat {\boldsymbol {I}} + 3 0 \hat {\boldsymbol {J}} - 5 0 \hat {\boldsymbol {K}} (\mathrm {m / s}) vO=−10I^+30J^−50K^(m/s)

aO=25I^+40J^−15K^(m/s2) \boldsymbol {a} _ {O} = 2 5 \hat {\boldsymbol {I}} + 4 0 \hat {\boldsymbol {J}} - 1 5 \hat {\boldsymbol {K}} (\mathrm {m} / \mathrm {s} ^ {2}) aO=25I^+40J^−15K^(m/s2)

运动坐标系的角速度和角加速度分别为

Ω=0.6I^−0.4J^+1.0K^(rad/s) \boldsymbol {\Omega} = 0. 6 \hat {\boldsymbol {I}} - 0. 4 \hat {\boldsymbol {J}} + 1. 0 \hat {\boldsymbol {K}} (\mathrm {r a d / s}) Ω=0.6I^−0.4J^+1.0K^(rad/s)

Ω˙=−0.4I^+0.3J^−1.0K^(rad/s2) \dot {\boldsymbol {\Omega}} = - 0. 4 \hat {\boldsymbol {I}} + 0. 3 \hat {\boldsymbol {J}} - 1. 0 \hat {\boldsymbol {K}} (\mathrm {r a d} / \mathrm {s} ^ {2}) Ω˙=−0.4I^+0.3J^−1.0K^(rad/s2)

运动坐标系的单位矢量为

t^=0.57735I^+0.57735J^+0.57735K^ \hat {\boldsymbol {t}} = 0. 5 7 7 3 5 \hat {\boldsymbol {I}} + 0. 5 7 7 3 5 \hat {\boldsymbol {J}} + 0. 5 7 7 3 5 \hat {\boldsymbol {K}} t^=0.57735I^+0.57735J^+0.57735K^

J^=−0.74296I^+0.66475J^+0.078206K^ \hat {\boldsymbol {J}} = - 0. 7 4 2 9 6 \hat {\boldsymbol {I}} + 0. 6 6 4 7 5 \hat {\boldsymbol {J}} + 0. 0 7 8 2 0 6 \hat {\boldsymbol {K}} J^=−0.74296I^+0.66475J^+0.078206K^

k^=−0.33864I^−0.47410J^+0.81274K^ \hat {\boldsymbol {k}} = - 0. 3 3 8 6 4 \hat {\boldsymbol {I}} - 0. 4 7 4 1 0 \hat {\boldsymbol {J}} + 0. 8 1 2 7 4 \hat {\boldsymbol {K}} k^=−0.33864I^−0.47410J^+0.81274K^

PPP 点的绝对位置矢量为

r=150I^−200J^+300K^(m) \boldsymbol {r} = 1 5 0 \hat {\boldsymbol {I}} - 2 0 0 \hat {\boldsymbol {J}} + 3 0 0 \hat {\boldsymbol {K}} (\mathrm {m}) r=150I^−200J^+300K^(m)

PPP 点相对于运动坐标系的速度和加速度分别为

v相 对=−20i^+25j^+70k^(m/s) \boldsymbol {v} _ {\text {相 对}} = - 2 0 \hat {\boldsymbol {i}} + 2 5 \hat {\boldsymbol {j}} + 7 0 \hat {\boldsymbol {k}} (\mathrm {m / s}) v相 对=−20i^+25j^+70k^(m/s)

a相 对=7.5i^−8.5j^+6.0k^(m/s2) \pmb {a} _ {\text {相 对}} = 7. 5 \hat {\pmb {i}} - 8. 5 \hat {\pmb {j}} + 6. 0 \hat {\pmb {k}} (\mathrm {m / s ^ {2}}) a相 对=7.5i^−8.5j^+6.0k^(m/s2)

求出 PPP 点的绝对速度 vP\pmb{v}{P}vP 和绝对加速度 aP\pmb{a}{P}aP 。

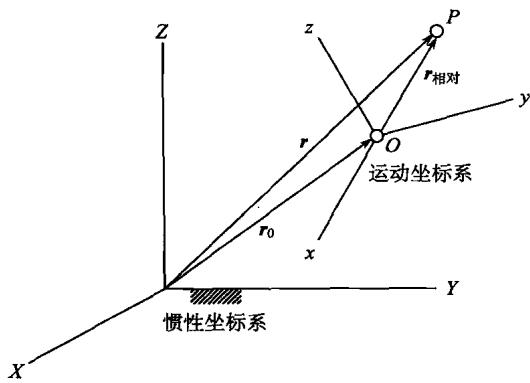
图P.1.3 解答与解析：

分析：

利用科里奥利定理求绝对速度和加速度。

已知惯性系基矢量 I^,J^,K^\hat{I}, \hat{J}, \hat{K}I^,J^,K^ 和运动系基矢量 i^,j^,k^\hat{i}, \hat{j}, \hat{k}i^,j^,k^ 的关系，首先构建坐标变换矩阵 Q\mathbf{Q}Q，将相对运动矢量转换到惯性系中。

Python 计算结果：

# 绝对速度 v_P

v_P = 256.1742\hat{I} + -268.1153\hat{J} + -302.7000\hat{K}

# 绝对加速度 a_P

a_P = 102.0040\hat{I} + 601.4236\hat{J} + 87.7429\hat{K}

详细步骤：

1. 相对位置 rrel=rP−rO=−150.0000I^+−400.0000J^+200.0000K^\boldsymbol{r}_{rel} = \boldsymbol{r}_P - \boldsymbol{r}_O = -150.0000\hat{I} + -400.0000\hat{J} + 200.0000\hat{K}rrel=rP−rO=−150.0000I^+−400.0000J^+200.0000K^ (m)

2. 相对速度 vrel\boldsymbol{v}_{rel}vrel (转到惯性系) = -53.8258\hat{I} + -28.1153\hat{J} + 47.3000\hat{K} (m/s)

3. 相对加速度 arel\boldsymbol{a}_{rel}arel (转到惯性系) = 8.6134\hat{I} + -4.1648\hat{J} + 8.5418\hat{K} (m/s²)

4. 代入公式计算得最终结果如上。

---

1.4 F\pmb{F}F 为作用在位于 xyxyxy 平面内的一做平面运动刚体上大小不变的力。在某一给定时刻， ω=3k^rad/s,ω˙=−2k^rad/s2,ω¨=0,F=10i^N\omega = 3\hat{k} \mathrm{rad/s}, \dot{\omega} = -2\hat{k} \mathrm{rad/s^2}, \ddot{\omega} = 0, F = 10\hat{i} \mathrm{N}ω=3k^rad/s,ω˙=−2k^rad/s2,ω¨=0,F=10i^N 。求此时的 F¨\ddot{F}F¨ 。

解答与解析：

已知 F=10i^\boldsymbol{F} = 10\hat{i}F=10i^ 固定在刚体上，ω=3k^\boldsymbol{\omega} = 3\hat{k}ω=3k^，ω˙=−2k^\dot{\boldsymbol{\omega}} = -2\hat{k}ω˙=−2k^。

求 F¨\ddot{\boldsymbol{F}}F¨。

F˙=ω×F\dot{\boldsymbol{F}} = \boldsymbol{\omega} \times \boldsymbol{F}F˙=ω×F

F¨=ω˙×F+ω×(ω×F)\ddot{\boldsymbol{F}} = \dot{\boldsymbol{\omega}} \times \boldsymbol{F} + \boldsymbol{\omega} \times (\boldsymbol{\omega} \times \boldsymbol{F})F¨=ω˙×F+ω×(ω×F)

Python 计算结果：

F¨=−90.0i^+−20.0j^+0.0k^\ddot{\boldsymbol{F}} = -90.0\hat{i} + -20.0\hat{j} + 0.0\hat{k}F¨=−90.0i^+−20.0j^+0.0k^ (N/s²)

---

1.5 如图 P.1.5 所示: 一距离地面高度为 hhh 的飞机, 以匀速 vvv 经过一雷达跟踪站 AAA 的上方。求出当飞机正好飞离此跟踪站时, 雷达天线的角速度 θ˙\dot{\theta}θ˙ , 角加速度 θ¨\ddot{\theta}θ¨ 和飞机的速率 r˙\dot{r}r˙ 。假设惯性坐标系设在地面上且不考虑地球自转, 运动坐标系固连在雷达天线上, 且 xxx 轴由雷达天线指向飞机。

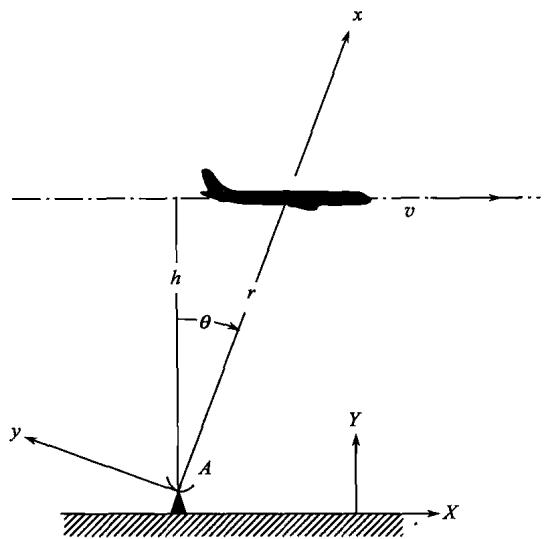
图P.1.5 解答与解析：

分析：

飞机位于雷达正上方，距离 hhh，速度 vvv 水平。

雷达天线跟踪飞机，故视线方向为天线 xxx 轴。

此时 r=hr = hr=h，θ=90∘\theta = 90^\circθ=90∘（假设水平为0）或 θ\thetaθ 为仰角此时为 90∘90^\circ90∘。

但在极坐标系中，通常 θ\thetaθ 是极角。设雷达在原点，飞机位置 (r,θ)(r, \theta)(r,θ)。

位置矢量 r=re^r\mathbf{r} = r \hat{e}_rr=re^r。

速度 v=r˙e^r+rθ˙e^θ\mathbf{v} = \dot{r} \hat{e}r + r \dot{\theta} \hat{e}\thetav=r˙e^r+rθ˙e^θ。

当飞机在正上方时，速度方向垂直于 r\mathbf{r}r（即垂直于 xxx 轴）。

所以 v\mathbf{v}v 只有 e^θ\hat{e}\thetae^θ 分量（或 −e^θ-\hat{e}\theta−e^θ，取决于定义）。

因此：

1. r˙=0\dot{r} = 0r˙=0 (径向速度为0，距离变化率为0)。

2. rθ˙=v  ⟹  θ˙=v/hr \dot{\theta} = v \implies \dot{\theta} = v/hrθ˙=v⟹θ˙=v/h。

加速度 a=(r¨−rθ˙2)e^r+(rθ¨+2r˙θ˙)e^θ\mathbf{a} = (\ddot{r} - r\dot{\theta}^2)\hat{e}r + (r\ddot{\theta} + 2\dot{r}\dot{\theta})\hat{e}\thetaa=(r¨−rθ˙2)e^r+(rθ¨+2r˙θ˙)e^θ。

飞机匀速直线运动，加速度为0。

所以：

r¨−rθ˙2=0  ⟹  r¨=h(v/h)2=v2/h\ddot{r} - r\dot{\theta}^2 = 0 \implies \ddot{r} = h (v/h)^2 = v^2/hr¨−rθ˙2=0⟹r¨=h(v/h)2=v2/h。

rθ¨+2r˙θ˙=0r\ddot{\theta} + 2\dot{r}\dot{\theta} = 0rθ¨+2r˙θ˙=0。已知 r˙=0\dot{r}=0r˙=0，则 rθ¨=0  ⟹  θ¨=0r\ddot{\theta} = 0 \implies \ddot{\theta} = 0rθ¨=0⟹θ¨=0。

结果：

• r˙=0\dot{r} = 0r˙=0

• θ˙=v/h\dot{\theta} = v/hθ˙=v/h

• θ¨=0\ddot{\theta} = 0θ¨=0

---

1.6 北纬 30∘30^{\circ}30∘ 处，一质量为 1000kg1000\mathrm{kg}1000kg 的汽车在标准海平面高度的水平公路上，以 100km/h100\mathrm{km/h}100km/h 的速度向正北方向匀速行驶。在考虑地球自转的情况下，求出路对汽车的侧向作用力和法向作用力。

解答与解析：

分析：

汽车向北行驶，受科里奥利力 Fcor=−2mΩ×vrel\mathbf{F}{cor} = -2m \boldsymbol{\Omega} \times \mathbf{v}{rel}Fcor=−2mΩ×vrel。

北纬 30∘30^\circ30∘，Ω\boldsymbol{\Omega}Ω 指向北天极。

分解 Ω\boldsymbol{\Omega}Ω：水平向北分量 Ωcos⁡ϕ\Omega \cos\phiΩcosϕ，垂直向上分量 Ωsin⁡ϕ\Omega \sin\phiΩsinϕ。

速度 vrel\mathbf{v}_{rel}vrel 水平向北。

Ω×vrel\boldsymbol{\Omega} \times \mathbf{v}_{rel}Ω×vrel：

• (水平北 Ωy\Omega_yΩy) ×\times× (水平北 vyv_yvy) = 0

• (垂直上 Ωz\Omega_zΩz) ×\times× (水平北 vyv_yvy) = 水平向西 (−x-x−x方向)

所以科里奥利力 Fcor\mathbf{F}_{cor}Fcor 方向为水平向东 (+x+x+x方向)。

大小 Fcor=2m(Ωsin⁡ϕ)vF_{cor} = 2m (\Omega \sin\phi) vFcor=2m(Ωsinϕ)v。

这是路面对汽车的侧向力？

如果不考虑侧滑，汽车受力平衡。科里奥利力向东推车，路面必须给车一个向西的摩擦力来平衡它？

不，科里奥利力是惯性力（在非惯性系中）。

在地球系（非惯性系）中建立方程：Fext+Fcor+Fcen+mg=marel\mathbf{F}{ext} + \mathbf{F}{cor} + \mathbf{F}{cen} + m\mathbf{g} = m \mathbf{a}{rel}Fext+Fcor+Fcen+mg=marel。

汽车匀速直线行驶，arel=0\mathbf{a}_{rel} = 0arel=0。

Fext\mathbf{F}{ext}Fext (路面作用力) =−(Fcor+... )= -(\mathbf{F}{cor} + \dots)=−(Fcor+...)。

科里奥利力向东（计算：−2m(Ωzk×vj)=−2mΩzv(−i)=2mΩzvi-2m (\Omega_z \mathbf{k} \times v \mathbf{j}) = -2m \Omega_z v (-\mathbf{i}) = 2m \Omega_z v \mathbf{i}−2m(Ωzk×vj)=−2mΩzv(−i)=2mΩzvi，即向东）。

等等，Fcor=−2mΩ×v\mathbf{F}_{cor} = -2m \boldsymbol{\Omega} \times \mathbf{v}Fcor=−2mΩ×v。

Ω×v\boldsymbol{\Omega} \times \mathbf{v}Ω×v 是向西的。所以 −2m...-2m \dots−2m... 是向东的。

所以路面需要提供向西的力来平衡这个"向东的力"。

法向力：考虑垂直方向。FN−mg+Fcor,z+Fcen,z=0\mathbf{F}N - mg + F{cor,z} + F_{cen,z} = 0FN−mg+Fcor,z+Fcen,z=0。

这里 Ω×v\boldsymbol{\Omega} \times \mathbf{v}Ω×v 没有垂直分量（因为 Ω\OmegaΩ 和 vvv 都在子午面内）。

但如果汽车向东开，就会有垂直分量（Eötvös效应）。向北开没有垂直科里奥利力。

所以法向力主要受离心力影响（通常包含在重力中）。

计算结果：

侧向力 (向西): 2.0256 N

法向力变化: -0.0000 N (此处为0，因为向北行驶无垂直科里奥利力)

---

1.7 如图P.1.7所示，北纬 29∘29^{\circ}29∘ 处，一长度 30m30\mathrm{m}30m 的细绳下悬挂一铅锤。由于地球自转的影响，求此铅锤偏离中心的距离 ddd 。

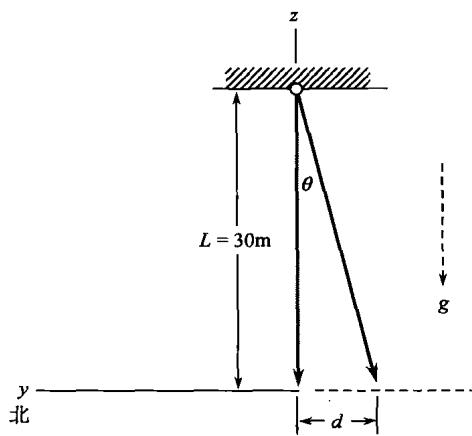
图P.1.7 解答与解析：

分析：

由于地球自转，铅垂线（悬挂静止物体）偏离地心方向。

偏离原因：离心力 Fcen=−mΩ×(Ω×r)\mathbf{F}_{cen} = -m \boldsymbol{\Omega} \times (\boldsymbol{\Omega} \times \mathbf{r})Fcen=−mΩ×(Ω×r)，方向垂直地轴向外。

在北半球，离心力指向南方和上方。

水平分量（向南）导致铅垂线向南偏。

偏角 θ≈Fcen,horiz/(mg)\theta \approx F_{cen, horiz} / (mg)θ≈Fcen,horiz/(mg)。

偏移距离 d=Lθd = L \thetad=Lθ。

计算结果：

偏移距离 d≈44.02d \approx 44.02d≈44.02 mm

(d=0.044023d = 0.044023d=0.044023 m)

---