卡拉兹函数 - 技术栈

文章目录

一、函数定义
二、用java实现下
三、总结

一、函数定义

背景：牛客网算法题里有个卡拉兹函数，感觉有点意思。

这个函数定义很简单，但是至今没人能穷尽证明；而且有些看似简单的数计算步骤却很多。我们目的是自己按照定义用java写一下，计算100、10w、100w以内的整数的归一情况，并找出100w以内归一步数最大的那个数和步数。

牛客网连接如下：

牛客网-算法-卡拉兹函数

二、用java实现下

要求：输入一个整数，输出的结果要知道当前计算的是哪个数？当前计算的数归一的步骤的每个数（以便知道需要多少步才能归1；同时缓存下来，循环大量数据的时候只要在缓存中出现过的必定归一，可以不用再重复计算）

呈现的效果类似这样：

java 复制代码

递归计算的结果是：{7:[7,22,11,34,17,52,26,13,40,20,10,5,16,8,4,2,1]}
 计算步数：17
 
【999999递归计算的结果是】：{999999:[999999,2999998,1499999,4499998,2249999,6749998,3374999,10124998,5062499,15187498,7593749,22781248,11390624,5695312,2847656,1423828,711914,355957,1067872,533936,266968,133484,66742,33371,100114,50057,150172,75086,37543,112630,56315,168946,84473,253420,126710,63355,190066,95033,285100,142550,71275,213826,106913,320740,160370,80185,240556,120278,60139,180418,90209,270628,135314,67657,202972,101486,50743,152230,76115,228346,114173,342520,171260,85630,42815,128446,64223,192670,96335,289006,144503,433510,216755,650266,325133,975400,487700,243850,121925,365776,182888,91444,45722,22861,68584,34292,17146,8573,25720,12860,6430,3215,9646,4823,14470,7235,21706,10853,32560,16280,8140,4070,2035,6106,3053,9160,4580,2290,1145,3436,1718,859,2578,1289,3868,1934,967,2902,1451,4354,2177,6532,3266,1633,4900,2450,1225,3676,1838,919,2758,1379,4138,2069,6208,3104,1552,776,388,194,97,292,146,73,220,110,55,166,83,250,125,376,188,94,47,142,71,214,107,322,161,484,242,121,364,182,91,274,137,412,206,103,310,155,466,233,700,350,175,526,263,790,395,1186,593,1780,890,445,1336,668,334,167,502,251,754,377,1132,566,283,850,425,1276,638,319,958,479,1438,719,2158,1079,3238,1619,4858,2429,7288,3644,1822,911,2734,1367,4102,2051,6154,3077,9232,4616,2308,1154,577,1732,866,433,1300,650,325,976,488,244,122,61,184,92,46,23,70,35,106,53,160,80,40,20,10,5,16,8,4,2,1]}
 计算步数：259
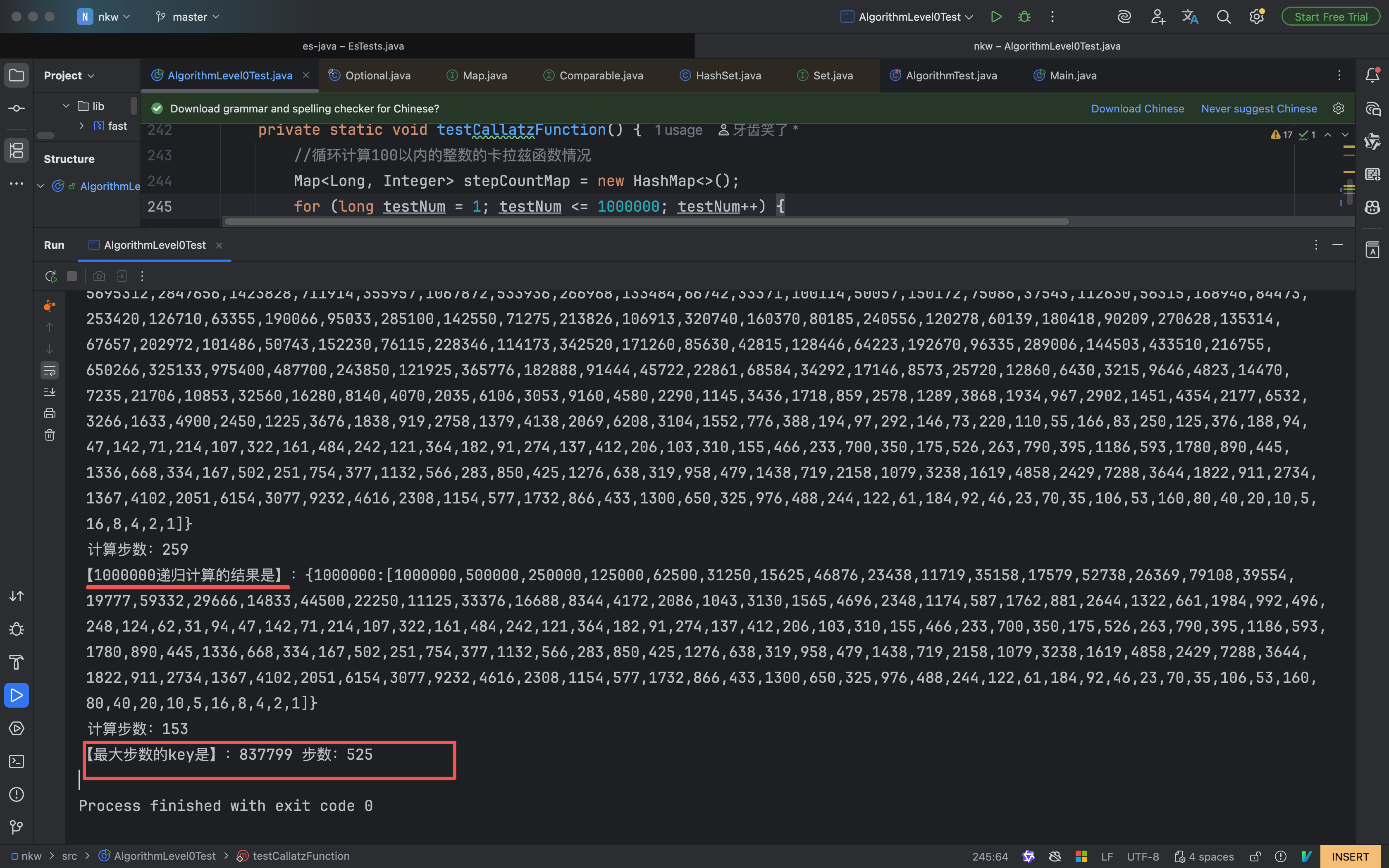
【1000000递归计算的结果是】：{1000000:[1000000,500000,250000,125000,62500,31250,15625,46876,23438,11719,35158,17579,52738,26369,79108,39554,19777,59332,29666,14833,44500,22250,11125,33376,16688,8344,4172,2086,1043,3130,1565,4696,2348,1174,587,1762,881,2644,1322,661,1984,992,496,248,124,62,31,94,47,142,71,214,107,322,161,484,242,121,364,182,91,274,137,412,206,103,310,155,466,233,700,350,175,526,263,790,395,1186,593,1780,890,445,1336,668,334,167,502,251,754,377,1132,566,283,850,425,1276,638,319,958,479,1438,719,2158,1079,3238,1619,4858,2429,7288,3644,1822,911,2734,1367,4102,2051,6154,3077,9232,4616,2308,1154,577,1732,866,433,1300,650,325,976,488,244,122,61,184,92,46,23,70,35,106,53,160,80,40,20,10,5,16,8,4,2,1]}
 计算步数：153
【最大步数的key是】：837799 步数：525

代码提交记录见：gitee

commitId : a2d647339fe6a2f7fad3726b4ca7a265574950cf
卡拉兹函数gitee提交记录

核心代码如下：

java 复制代码

/**
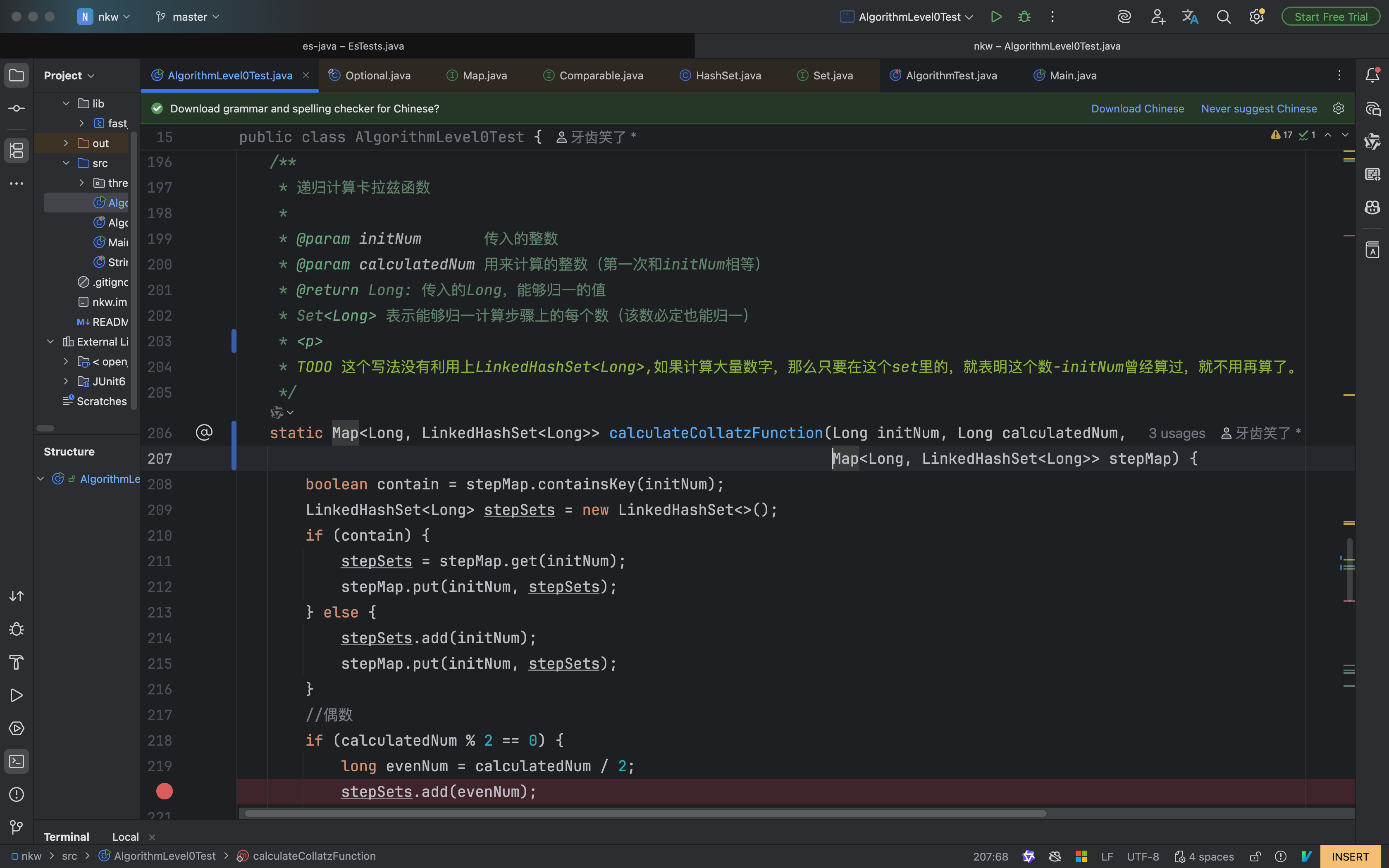
     * 递归计算卡拉兹函数
     *
     * @param initNum       传入的整数
     * @param calculatedNum 用来计算的整数（第一次和initNum相等）
     * @return Long: 传入的Long，能够归一的值
     * Set<Long> 表示能够归一计算步骤上的每个数（该数必定也能归一）
     * <p>
     * TODO 这个写法没有利用上LinkedHashSet<Long>,如果计算大量数字，那么只要在这个set里的，就表明这个数-initNum曾经算过，就不用再算了。
     */
    static Map<Long, LinkedHashSet<Long>> calculateCollatzFunction(Long initNum, Long calculatedNum, Map<Long, LinkedHashSet<Long>> stepMap) {
        boolean contain = stepMap.containsKey(initNum);
        LinkedHashSet<Long> stepSets = new LinkedHashSet<>();
        if (contain) {
            stepSets = stepMap.get(initNum);
            stepMap.put(initNum, stepSets);
        } else {
            stepSets.add(initNum);
            stepMap.put(initNum, stepSets);
        }
        //偶数
        if (calculatedNum % 2 == 0) {
            long evenNum = calculatedNum / 2;
            stepSets.add(evenNum);
            if (evenNum == 1) {
                return stepMap;
                //递归
            } else {
                return calculateCollatzFunction(initNum, evenNum, stepMap);
            }
            //奇数
        } else {
            long oddNum = 3 * calculatedNum + 1;
            stepSets.add(oddNum);
            if (oddNum == 1) {
                return stepMap;
                //递归
            } else {
                return calculateCollatzFunction(initNum, oddNum, stepMap);
            }
        }
    }

java 复制代码

   /**
     * 测试卡拉兹函数
     */
    private static void testCallatzFunction() {
        //循环计算100以内的整数的卡拉兹函数情况
        Map<Long, Integer> stepCountMap = new HashMap<>();
        for (long testNum = 1; testNum <= 1000000; testNum++) {
            Map<Long, LinkedHashSet<Long>> stepMap = new HashMap<>();
            Map<Long, LinkedHashSet<Long>> resultMap = calculateCollatzFunction(testNum, testNum, stepMap);
            System.out.println("【" + testNum + "递归计算的结果是】：" + JSON.toJSONString(resultMap) + "\n 计算步数：" + resultMap.get(testNum).size());
            stepCountMap.put(testNum, resultMap.get(testNum).size());
        }
        //找出100w以内卡拉兹归一步数最多的那个数。
        Optional<Map.Entry<Long, Integer>> max = stepCountMap.entrySet().stream().max(Map.Entry.comparingByValue());
        max.ifPresent(longIntegerEntry -> System.out.println("【最大步数的key是】：" + longIntegerEntry.getKey() + " 步数：" + longIntegerEntry.getValue()));
    }

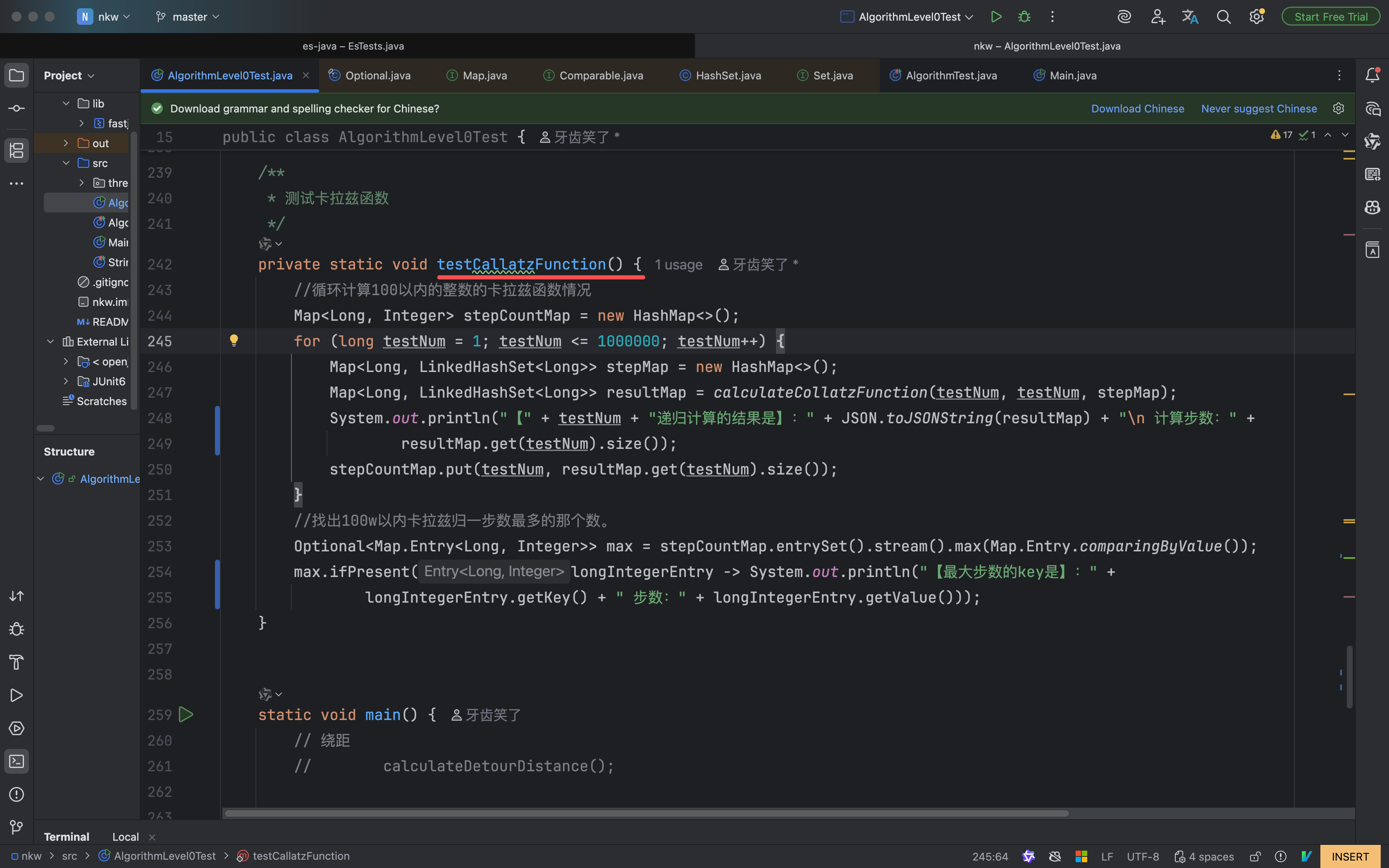
看下100万以内（耗时不久，1-2分钟左右）哪个数归一步数最多？

结论是：100万以内，卡拉兹归一步数最多的数是：837799

步数：525

具体部署如下：

java 复制代码

递归计算的结果是：{837799:[837799,2513398,1256699,3770098,1885049,5655148,2827574,1413787,4241362,2120681,6362044,3181022,1590511,4771534,2385767,7157302,3578651,10735954,5367977,16103932,8051966,4025983,12077950,6038975,18116926,9058463,27175390,13587695,40763086,20381543,61144630,30572315,91716946,45858473,137575420,68787710,34393855,103181566,51590783,154772350,77386175,232158526,116079263,348237790,174118895,522356686,261178343,783535030,391767515,1175302546,587651273,1762953820,881476910,440738455,1322215366,661107683,1983323050,991661525,2974984576,1487492288,743746144,371873072,185936536,92968268,46484134,23242067,69726202,34863101,104589304,52294652,26147326,13073663,39220990,19610495,58831486,29415743,88247230,44123615,132370846,66185423,198556270,99278135,297834406,148917203,446751610,223375805,670127416,335063708,167531854,83765927,251297782,125648891,376946674,188473337,565420012,282710006,141355003,424065010,212032505,636097516,318048758,159024379,477073138,238536569,715609708,357804854,178902427,536707282,268353641,805060924,402530462,201265231,603795694,301897847,905693542,452846771,1358540314,679270157,2037810472,1018905236,509452618,254726309,764178928,382089464,191044732,95522366,47761183,143283550,71641775,214925326,107462663,322387990,161193995,483581986,241790993,725372980,362686490,181343245,544029736,272014868,136007434,68003717,204011152,102005576,51002788,25501394,12750697,38252092,19126046,9563023,28689070,14344535,43033606,21516803,64550410,32275205,96825616,48412808,24206404,12103202,6051601,18154804,9077402,4538701,13616104,6808052,3404026,1702013,5106040,2553020,1276510,638255,1914766,957383,2872150,1436075,4308226,2154113,6462340,3231170,1615585,4846756,2423378,1211689,3635068,1817534,908767,2726302,1363151,4089454,2044727,6134182,3067091,9201274,4600637,13801912,6900956,3450478,1725239,5175718,2587859,7763578,3881789,11645368,5822684,2911342,1455671,4367014,2183507,6550522,3275261,9825784,4912892,2456446,1228223,3684670,1842335,5527006,2763503,8290510,4145255,12435766,6217883,18653650,9326825,27980476,13990238,6995119,20985358,10492679,31478038,15739019,47217058,23608529,70825588,35412794,17706397,53119192,26559596,13279798,6639899,19919698,9959849,29879548,14939774,7469887,22409662,11204831,33614494,16807247,50421742,25210871,75632614,37816307,113448922,56724461,170173384,85086692,42543346,21271673,63815020,31907510,15953755,47861266,23930633,71791900,35895950,17947975,53843926,26921963,80765890,40382945,121148836,60574418,30287209,90861628,45430814,22715407,68146222,34073111,102219334,51109667,153329002,76664501,229993504,114996752,57498376,28749188,14374594,7187297,21561892,10780946,5390473,16171420,8085710,4042855,12128566,6064283,18192850,9096425,27289276,13644638,6822319,20466958,10233479,30700438,15350219,46050658,23025329,69075988,34537994,17268997,51806992,25903496,12951748,6475874,3237937,9713812,4856906,2428453,7285360,3642680,1821340,910670,455335,1366006,683003,2049010,1024505,3073516,1536758,768379,2305138,1152569,3457708,1728854,864427,2593282,1296641,3889924,1944962,972481,2917444,1458722,729361,2188084,1094042,547021,1641064,820532,410266,205133,615400,307700,153850,76925,230776,115388,57694,28847,86542,43271,129814,64907,194722,97361,292084,146042,73021,219064,109532,54766,27383,82150,41075,123226,61613,184840,92420,46210,23105,69316,34658,17329,51988,25994,12997,38992,19496,9748,4874,2437,7312,3656,1828,914,457,1372,686,343,1030,515,1546,773,2320,1160,580,290,145,436,218,109,328,164,82,41,124,62,31,94,47,142,71,214,107,322,161,484,242,121,364,182,91,274,137,412,206,103,310,155,466,233,700,350,175,526,263,790,395,1186,593,1780,890,445,1336,668,334,167,502,251,754,377,1132,566,283,850,425,1276,638,319,958,479,1438,719,2158,1079,3238,1619,4858,2429,7288,3644,1822,911,2734,1367,4102,2051,6154,3077,9232,4616,2308,1154,577,1732,866,433,1300,650,325,976,488,244,122,61,184,92,46,23,70,35,106,53,160,80,40,20,10,5,16,8,4,2,1]}
 计算步数：525

三、总结

牛客网的算法题，有的小巧的算法里隐藏着有趣的思想，可以略微多探索一下。