队列-优先队列【Queue3】

下午开始肝，忘记的好多哈哈，第二篇

1、什么是优先队列？

想象一下在机场办理登机手续。通常情况下，乘客们会排成一条队，遵循"先来后到"的原则，这就像一个普通的"队列"(Queue)。

但是，如果航空公司为头等舱或商务舱的乘客开设了优先通道，那么无论这些乘客什么时候到达，他们总能比经济舱的乘客更早办理手续。这时候，队伍的顺序就不再仅仅由到达时间决定，而是由一个更重要的因素------"舱位等级"或"优先级"------来决定。

优先队列 就是这样一种抽象数据类型。它和普通队列类似，都可以存入和取出数据。但不同的是，它在取出元素时，遵循的不是"先进先出"(FIFO)的规则，而是最高优先级的元素最先出队。

每个进入优先队列的元素都会被赋予一个"优先级"。当我们请求下一个元素时，优先队列会返回并移除队列中当前优先级最高的那个元素。

2、为什么需要优先队列？

优先队列是许多高效算法的基石，应用非常广泛：

1. Dijkstra最短路径算法: 在图中寻找两个节点之间的最短路径。优先队列用于存储待访问的节点，每次都优先处理距离起点最近的节点。
2. Prim最小生成树算法: 与Dijkstra类似，用于选择权重最小的边来构建树。
3. 任务调度系统: 操作系统需要决定下一个要执行哪个任务。高优先级的任务（如系统进程）应该比低优先级的任务（如后台下载）先被执行。
4. 数据压缩（霍夫曼编码）: 通过优先队列构建最优前缀码树，出现频率最高的字符会被赋予最短的编码，从而实现高效压缩。
5. 事件驱动模拟: 在模拟系统中，用于管理未来的事件，每次都从队列中取出时间最早（优先级最高）的事件进行处理。

3、优先队列的实现方式

有几种常见的思路，但它们的效率差异巨大。

3.1、方案一：使用无序数组

最简单的想法，就是用一个普通数组来存储元素，不关心它们的顺序。

• 插入: 非常快。直接将新元素添加到数组末尾即可。时间复杂度为 O(1)。
• 提取最大值: 非常慢。因为元素是无序的，我们必须遍历整个数组，找到那个优先级最高的元素，然后才能将它返回并删除。时间复杂度为 O(n)。

:::info

如果插入操作非常频繁，而提取操作很少，这或许可以接受。但在大多数场景下，提取操作的 O(n) 复杂度是无法忍受的性能瓶颈。

:::

3.2、方案二：使用有序数组

为了解决提取慢的问题，我们可以时刻保持数组有序（按优先级从高到低排序）。

• 插入: 变慢了。为了维持有序性，我们需要找到新元素的正确插入位置，并将之后的所有元素向后移动一位。平均时间复杂度为 O(n)。
• 提取最大值: 变得飞快。因为数组总是有序的，优先级最高的元素总是在数组的头部或尾部。直接取出即可。时间复杂度为 O(1)。

我们只是把性能瓶颈从提取操作转移到了插入操作。对于需要频繁插入和提取的场景，O(n) 的复杂度依然太高。

我们需要一种数据结构，它能在插入和提取这两个核心操作上都保持高效 。这就是下面要讲的主角------二叉堆。

4、最佳实践：二叉堆

二叉堆是一种特殊的、基于树的数据结构，它完美地平衡了插入和删除的效率，使得这两个操作的时间复杂度都能达到 O(log n) 级别，这是一个巨大的飞跃。

4.1、什么是堆？

这里先简单讲解一下，后面会详解讲解。

一个二叉堆必须满足两个核心属性：

1. 结构属性：它是一棵完全二叉树。
   这意味着树的每一层都是满的，除了可能的最后一层。并且最后一层的节点都尽可能地靠左排列。
2. 堆属性：父节点的值总是大于等于（或小于等于）其子节点的值。
   • 最大堆 (Max-Heap): 父节点的值 ≥ 子节点的值。因此，根节点总是整个堆中最大的元素。
   • 最小堆 (Min-Heap): 父节点的值 ≤ 子节点的值。因此，根节点总是整个堆中最小的元素。

我们通常使用最大堆 来实现提取最大值的优先队列，用最小堆 实现提取最小值的优先队列。下面的讨论将以最大堆为例。

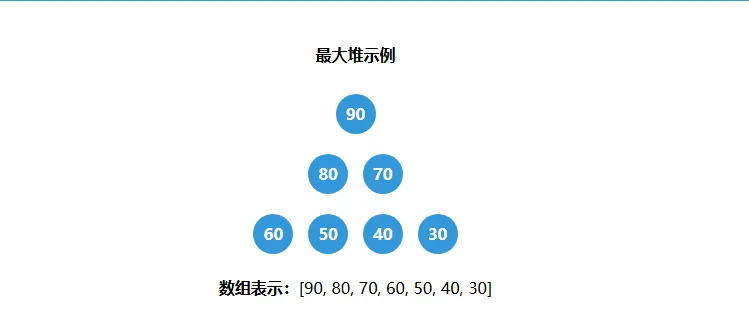
4.2、用数组表示堆

虽然堆在逻辑上是一棵树，但我们几乎从不使用传统的树节点（包含左右指针）来实现它。我们用一个简单的数组就够了。

为什么可以这么做？ 因为堆是完全二叉树，它的结构非常规整，节点在数组中的位置有明确的映射关系。对于数组中任意位置为i的节点：

• 其父节点的位置是(i - 1) / 2
• 其左子节点的位置是2 * i + 1
• 其右子节点的位置是2 * i + 2

这种方式的好处是：

• 节省空间：不需要额外的指针来维护节点关系。
• 高效访问：通过简单的数学计算就能快速定位父子节点，比指针跳转更快。
• 缓存友好：数组在内存中是连续存储的，这能更好地利用CPU缓存。

例如，一个逻辑上的堆 可以被看作如下的树形结构：

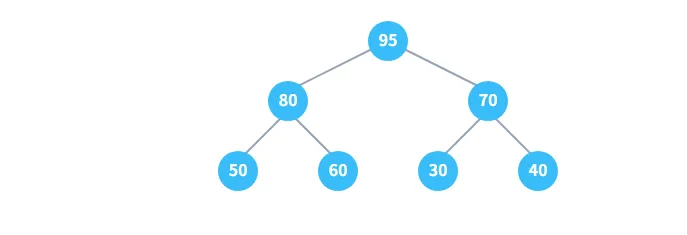
5、核心操作

5.1、插入操作：上浮

当我们要插入一个新元素时（例如，插入 90），为了维持堆的结构，我们遵循以下步骤：

1. 添加到末尾: 将新元素放在数组的最后，以保持完全二叉树的结构。
2. 比较与交换: 将新元素与其父节点比较。如果新元素比父节点大（在最大堆中），就交换它们的位置。
3. 重复上浮: 继续将该元素与其新的父节点比较和交换，直到它不再大于其父节点，或者它已经到达了根的位置。

为什么叫"上浮"？

因为这个过程就像一个气泡从水底不断上浮，直到找到自己合适的位置。这个操作确保了在插入新元素后，堆属性依然被满足。

5.2、提取最大值操作：下沉

提取最大值的操作稍微复杂一些，因为我们要移除的是根节点，这会破坏树的结构。

1. 记录最大值: 根节点就是最大值，我们先保存它，因为这是要返回的结果。
2. 替换根节点: 将数组的最后一个元素移动到根的位置。这样做是为了保持完全二叉树的结构，避免树中出现"空洞"。
3. 比较与交换: 新的根节点可能非常小，破坏了堆属性。因此，我们需要将它与它的两个子节点中较大的那个进行比较。如果它比那个较大的子节点小，就交换它们。
4. 重复下沉: 继续将这个元素与其新的子节点比较和交换，直到它不再小于其任何一个子节点，或者它已经成为一个叶子节点。

为什么叫"下沉"？

因为这个过程就像一块石头，从水面不断下沉，直到找到它稳定的位置。这个操作确保了在移除最大元素后，堆能重新组织成一个有效的最大堆。

6、Java实现

下面是两个使用 Java 从零开始实现的最大堆优先队列。

示例1：

package duilie;

import java.util.ArrayList;
import java.util.List;

/**
 * 优先队列
 */
public class MaxPriorityQueue {
    // 使用ArrayList作为底层存储结构
    private List<Integer> heap;

    /**
     * 构造方法：初始化空的最大优先队列
     */
    public MaxPriorityQueue() {
        heap = new ArrayList<>();
    }

    /**
     * 插入一个新元素，并执行上浮操作来维持堆属性。
     * 时间复杂度: O(log n)
     * @param value 要插入的整数值
     */
    public void insert(int value) {
        // 1. 将新元素添加到列表末尾
        heap.add(value);
        // 2. 对新元素执行上浮操作
        siftUp(heap.size() - 1);
    }

    /**
     * 提取并返回最大元素，并执行下沉操作来重新构建堆。
     * 时间复杂度: O(log n)
     * @return 堆中的最大值，如果堆为空返回 null
     */
    public Integer extractMax() {
        if (heap.isEmpty()) {
            return null;
        }

        // 如果堆中只有一个元素，直接移除并返回
        if (heap.size() == 1) {
            return heap.remove(heap.size() - 1);
        }

        // 1. 保存根节点（最大值）
        Integer maxValue = heap.get(0);
        // 2. 将最后一个元素移动到根部，并移除最后一个元素
        heap.set(0, heap.remove(heap.size() - 1));
        // 3. 对新的根执行下沉操作
        siftDown(0);

        return maxValue;
    }

    /**
     * 返回最大值但不移除。时间复杂度: O(1)
     * @return 堆中的最大值，如果堆为空返回 null
     */
    public Integer peekMax() {
        return heap.isEmpty() ? null : heap.get(0);
    }

    /**
     * 返回队列大小。时间复杂度: O(1)
     * @return 队列中的元素数量
     */
    public int size() {
        return heap.size();
    }

    /**
     * 上浮操作：将指定索引的节点向上移动，直到满足堆属性。
     * @param index 需要上浮的节点索引
     */
    private void siftUp(int index) {
        int parentIndex = (index - 1) / 2;
        // 当节点不是根节点，并且比其父节点大时，持续上浮
        while (index > 0 && heap.get(index) > heap.get(parentIndex)) {
            // 交换当前节点和父节点
            swap(index, parentIndex);
            // 更新当前节点的索引为其父节点的索引，继续向上检查
            index = parentIndex;
            parentIndex = (index - 1) / 2;
        }
    }

    /**
     * 下沉操作：将指定索引的节点向下移动，直到满足堆属性。
     * @param index 需要下沉的节点索引
     */
    private void siftDown(int index) {
        int maxIndex = index;
        while (true) {
            int leftChildIndex = 2 * index + 1;
            int rightChildIndex = 2 * index + 2;

            // 检查左子节点是否存在且大于当前最大值节点
            if (leftChildIndex < heap.size() && heap.get(leftChildIndex) > heap.get(maxIndex)) {
                maxIndex = leftChildIndex;
            }

            // 检查右子节点是否存在且大于当前最大值节点
            if (rightChildIndex < heap.size() && heap.get(rightChildIndex) > heap.get(maxIndex)) {
                maxIndex = rightChildIndex;
            }

            // 如果最大的节点就是当前节点自己，说明下沉结束
            if (maxIndex == index) {
                break;
            }

            // 否则，交换并继续下沉
            swap(index, maxIndex);
            index = maxIndex;
        }
    }

    /**
     * 交换列表中两个元素的位置
     * @param i 第一个元素索引
     * @param j 第二个元素索引
     */
    private void swap(int i, int j) {
        int temp = heap.get(i);
        heap.set(i, heap.get(j));
        heap.set(j, temp);
    }

    /**
     * 获取当前堆的底层数组（用于测试输出）
     * @return 堆的底层ArrayList
     */
    public List<Integer> getHeap() {
        return new ArrayList<>(heap); // 返回副本，避免外部修改
    }

    public static void main(String[] args) {
        // --- 使用示例（和Python版本完全一致）---
        MaxPriorityQueue pq = new MaxPriorityQueue();
        pq.insert(45);
        pq.insert(20);
        pq.insert(14);
        pq.insert(12);
        pq.insert(31);
        pq.insert(7);
        pq.insert(11);
        pq.insert(13);
        pq.insert(90); // 插入一个很大的值

        System.out.println("当前堆数组: " + pq.getHeap());
        System.out.println("提取最大值: " + pq.extractMax()); // 应该输出 90
        System.out.println("提取后堆数组: " + pq.getHeap());
        System.out.println("再次提取最大值: " + pq.extractMax()); // 应该输出 45
        System.out.println("再次提取后堆数组: " + pq.getHeap());
    }
}

当前堆数组: [90, 45, 14, 31, 20, 7, 11, 12, 13]
提取最大值: 90
提取后堆数组: [45, 31, 14, 13, 20, 7, 11, 12]
再次提取最大值: 45
再次提取后堆数组: [31, 20, 14, 13, 12, 7, 11]

示例2：

package duilie;

/**
 * 优先队列
 * @param <T>
 */
public class MaxHeapPriorityQueue<T extends Comparable<T>> {
    // 存储堆元素的数组
    private T[] heap;
    // 堆中当前元素的数量
    private int size;
    // 堆的初始容量
    private static final int DEFAULT_CAPACITY = 10;

    // 构造方法：初始化空的优先队列
    public MaxHeapPriorityQueue() {
        heap = (T[]) new Comparable[DEFAULT_CAPACITY];
        size = 0;
    }

    // 构造方法：用已有数组初始化优先队列（堆化）
    public MaxHeapPriorityQueue(T[] array) {
        if (array == null || array.length == 0) {
            heap = (T[]) new Comparable[DEFAULT_CAPACITY];
            size = 0;
            return;
        }
        // 扩容到合适的大小
        heap = (T[]) new Comparable[Math.max(DEFAULT_CAPACITY, array.length)];
        System.arraycopy(array, 0, heap, 0, array.length);
        size = array.length;
        // 从最后一个非叶子节点开始堆化
        for (int i = (size - 2) / 2; i >= 0; i--) {
            sink(i);
        }
    }

    // 判断队列是否为空
    public boolean isEmpty() {
        return size == 0;
    }

    // 获取队列元素数量
    public int size() {
        return size;
    }

    // 入队：添加元素到优先队列
    public void enqueue(T element) {
        if (element == null) {
            throw new IllegalArgumentException("元素不能为null");
        }
        // 数组满了就扩容（2倍）
        if (size == heap.length) {
            resize(2 * heap.length);
        }
        // 把元素放到数组末尾
        heap[size] = element;
        size++;
        // 上浮调整，维持最大堆特性
        swim(size - 1);
    }

    // 出队：移除并返回优先级最高的元素（堆顶）
    public T dequeue() {
        if (isEmpty()) {
            throw new IllegalStateException("优先队列为空，无法出队");
        }
        // 堆顶元素是最大值
        T max = heap[0];
        // 用最后一个元素替换堆顶
        swap(0, size - 1);
        // 清空最后一个位置，避免内存泄漏
        heap[size - 1] = null;
        size--;
        // 下沉调整，维持最大堆特性
        sink(0);
        // 如果元素数量过少，缩容（节省内存）
        if (size > 0 && size == heap.length / 4) {
            resize(heap.length / 2);
        }
        return max;
    }

    // 查看堆顶元素（不删除）
    public T peek() {
        if (isEmpty()) {
            throw new IllegalStateException("优先队列为空");
        }
        return heap[0];
    }

    // 上浮操作：将索引k的元素向上调整，直到满足最大堆特性
    private void swim(int k) {
        // 只要不是根节点，且当前节点大于父节点，就交换
        while (k > 0 && compare(heap[k], heap[(k - 1) / 2]) > 0) {
            swap(k, (k - 1) / 2);
            k = (k - 1) / 2; // 移动到父节点索引
        }
    }

    // 下沉操作：将索引k的元素向下调整，直到满足最大堆特性
    private void sink(int k) {
        while (true) {
            int left = 2 * k + 1;  // 左子节点索引
            int right = 2 * k + 2; // 右子节点索引
            int largest = k;       // 记录当前节点、左/右子节点中最大值的索引

            // 比较左子节点
            if (left < size && compare(heap[left], heap[largest]) > 0) {
                largest = left;
            }
            // 比较右子节点
            if (right < size && compare(heap[right], heap[largest]) > 0) {
                largest = right;
            }
            // 如果最大值就是当前节点，无需继续下沉
            if (largest == k) {
                break;
            }
            // 交换当前节点和最大值节点
            swap(k, largest);
            k = largest; // 移动到最大值节点索引，继续下沉
        }
    }

    // 交换堆中两个位置的元素
    private void swap(int i, int j) {
        T temp = heap[i];
        heap[i] = heap[j];
        heap[j] = temp;
    }

    // 比较两个元素的大小（复用Comparable接口）
    private int compare(T a, T b) {
        return a.compareTo(b);
    }

    // 调整数组容量
    private void resize(int newCapacity) {
        T[] newHeap = (T[]) new Comparable[newCapacity];
        System.arraycopy(heap, 0, newHeap, 0, size);
        heap = newHeap;
    }

    // 测试方法
    public static void main(String[] args) {
        // 测试1：基础入队出队
        MaxHeapPriorityQueue<Integer> pq = new MaxHeapPriorityQueue<>();
        pq.enqueue(5);
        pq.enqueue(3);
        pq.enqueue(8);
        pq.enqueue(1);
        System.out.println("堆顶元素：" + pq.peek()); // 输出8
        System.out.println("出队元素：" + pq.dequeue()); // 输出8
        System.out.println("堆顶元素：" + pq.peek()); // 输出5
        System.out.println("队列大小：" + pq.size()); // 输出3

        // 测试2：批量出队（验证顺序）
        while (!pq.isEmpty()) {
            System.out.print(pq.dequeue() + " "); // 输出5 3 1
        }
        System.out.println();

        // 测试3：用数组初始化堆
        Integer[] arr = {2, 7, 4, 1, 8, 1};
        MaxHeapPriorityQueue<Integer> pq2 = new MaxHeapPriorityQueue<>(arr);
        System.out.println("数组初始化后的堆顶：" + pq2.peek()); // 输出8
    }
}

堆顶元素：8
出队元素：8
堆顶元素：5
队列大小：3
5 3 1 
数组初始化后的堆顶：8

7、Java中堆的实现原理

底层数据结构：基于数组的完全二叉堆

PriorityQueue 是 Java 集合框架中实现优先队列的核心类，其底层存储依赖动态扩容的 Object 数组 （源码中为 Object[] queue），逻辑上组织成一棵完全二叉树（堆结构），这是实现优先级排序的核心基础：

• 索引 i 的左子节点索引：2 * i + 1
• 索引 i 的右子节点索引：2 * i + 2
• 索引 i 的父节点索引：(i - 1) / 2（整数除法，自动向下取整）
• 堆的根节点固定在数组索引 0 位置，默认情况下该位置始终存储优先级最高（数值最小）的元素；若自定义比较器实现最大堆，则根节点存储数值最大的元素。

核心源码骨架（简化）：

public class PriorityQueue<E> extends AbstractQueue<E> {
    // 底层存储堆元素的数组
    transient Object[] queue;
    // 队列中当前元素数量
    private int size = 0;
    // 自定义比较器（null 时使用元素自身的 Comparable 接口）
    private final Comparator<? super E> comparator;
    // 默认初始容量（JDK 8 及以上固定为 11）
    private static final int DEFAULT_INITIAL_CAPACITY = 11;

    // 无参构造：默认初始容量 + 自然排序（最小堆）
    public PriorityQueue() {
        this(DEFAULT_INITIAL_CAPACITY, null);
    }

    // 带比较器的构造：自定义排序规则（如最大堆）
    public PriorityQueue(Comparator<? super E> comparator) {
        this(DEFAULT_INITIAL_CAPACITY, comparator);
    }
}

核心特性详解

1. 容量与扩容机制

PriorityQueue 的数组容量会动态调整，适配元素数量变化：

• 初始容量 ：无参构造默认初始化容量为 11；也可通过构造方法手动指定初始容量（如 new PriorityQueue<>(100)）。
• 扩容规则 （JDK 8+ 标准实现）：
  • 当数组当前容量 < 64 时，扩容后容量 = 旧容量 × 2 + 2（例如 11 → 24、24 → 50）；
  • 当数组当前容量 ≥ 64 时，扩容后容量 = 旧容量 × 1.5（例如 64 → 96、96 → 144）；
• 扩容本质是新建更大的数组，将原数组元素复制到新数组，时间复杂度为 O(n)，但扩容频率低，不影响堆核心操作（O(log n)）的整体性能。

2. 排序规则：自然排序 vs 定制排序

PriorityQueue 支持两种优先级排序方式，二者互斥：

• 自然排序 ：未传入自定义 Comparator 时（comparator = null），要求队列中的元素必须实现 Comparable 接口（如 Integer、String、Long 等基础类型包装类），否则运行时会抛出 ClassCastException。此时默认按"升序"构建最小堆，根节点为最小值。
• 定制排序 ：传入自定义 Comparator 接口实现（如 lambda 表达式、匿名内部类），无需元素实现 Comparable，优先级规则完全由比较器定义（例如实现最大堆、按对象的指定字段排序）。

3. 线程安全特性

PriorityQueue 是非线程安全的集合类：

• 多线程环境下同时执行"添加/删除/修改"操作，会导致堆结构破坏（如失去堆的父/子节点大小特性），引发数据错乱；
• 线程安全替代方案：使用 java.util.concurrent.PriorityBlockingQueue（基于 PriorityQueue 扩展，内置锁机制，支持阻塞式操作）。

4. 元素约束：不允许存储 null

PriorityQueue 严格禁止存入 null 元素：调用 add(null) 或 offer(null) 会直接抛出 NullPointerException，因为 null 无法参与比较（无论是 Comparable 还是 Comparator），会破坏堆的排序逻辑。

核心方法的内部实现

1. 入队操作：add(E e) / offer(E e)

add() 底层直接调用 offer()，二者功能一致（add() 失败时抛异常，offer() 返回 false），核心逻辑是尾插元素 + 上浮调整：

public boolean offer(E e) {
    // 校验 null 元素
    if (e == null)
        throw new NullPointerException();
    int i = size;
    // 容量不足时触发扩容
    if (i >= queue.length)
        grow(i + 1);
    size = i + 1;
    // 堆为空时，直接将元素放在根节点
    if (i == 0)
        queue[0] = e;
    else
        // 上浮操作：将新元素调整到合适位置，维持堆特性
        siftUp(i, e);
    return true;
}

// 上浮核心逻辑（简化）
private void siftUp(int k, E x) {
    if (comparator != null) {
        // 自定义比较器的上浮逻辑
        siftUpUsingComparator(k, x);
    } else {
        // 自然排序的上浮逻辑
        siftUpComparable(k, x);
    }
}

• 上浮（siftUp）：新元素插入数组末尾后，不断与父节点比较，若不满足堆特性则交换位置，直到找到合适的父节点或到达根节点。

2. 出队操作：poll()

核心逻辑是根节点出队 + 最后一个元素移至根节点 + 下沉调整：

public E poll() {
    if (size == 0)
        return null;
    int s = --size;
    // 保存根节点（要返回的优先级最高元素）
    E result = (E) queue[0];
    // 取数组最后一个元素
    E x = (E) queue[s];
    // 清空最后一个位置，避免内存泄漏
    queue[s] = null;
    if (s != 0)
        // 下沉操作：将新根节点调整到合适位置，维持堆特性
        siftDown(0, x);
    return result;
}

• 下沉（siftDown）：根节点被替换后，不断与左右子节点中"优先级更高"的节点比较，若不满足堆特性则交换位置，直到找到合适的子节点或到达叶子节点。

3. 查看堆顶：peek()

直接返回数组索引 0 的元素，不修改堆结构，时间复杂度 O(1)：

public E peek() {
    return (size == 0) ? null : (E) queue[0];
}

4. 移除指定元素：remove(Object o)

该方法用于移除队列中指定的元素，逻辑比 poll() 更复杂：

1. 遍历数组找到目标元素的索引 i（时间复杂度 O(n)）；
2. 若目标元素是数组最后一个元素，直接删除即可；
3. 若不是，用最后一个元素替换索引 i 的元素，然后根据元素大小执行"上浮"或"下沉"调整；
4. 整体时间复杂度：O(n)（遍历） + O(log n)（调整）。

关键使用注意事项

1. 遍历操作不保证有序

PriorityQueue 的迭代器（iterator()）是按数组物理存储顺序遍历，而非优先级顺序。若需按优先级遍历，必须通过 poll() 逐个弹出元素：

public static void main(String[] args) {
    // 构建最大堆
    PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Comparator.reverseOrder());
    maxHeap.add(3);
    maxHeap.add(1);
    maxHeap.add(2);
    
    // 迭代器遍历（无序，输出：3 1 2）
    for (Integer num : maxHeap) {
        System.out.print(num + " ");
    }
    
    // poll() 弹出（有序，输出：3 2 1）
    System.out.println("\n按优先级弹出：");
    while (!maxHeap.isEmpty()) {
        System.out.print(maxHeap.poll() + " ");
    }
}

2. 可变对象修改会破坏堆结构

若队列中的元素是可变对象（如自定义的实体类），修改影响优先级的字段后，堆不会自动重新调整，导致优先级逻辑失效：

// 自定义可变元素类
class Student implements Comparable<Student> {
    int score; // 按分数排序（分数越低，优先级越高）
    public Student(int score) { this.score = score; }
    
    @Override
    public int compareTo(Student o) {
        return Integer.compare(this.score, o.score);
    }
}

public static void main(String[] args) {
    PriorityQueue<Student> pq = new PriorityQueue<>();
    Student s1 = new Student(90);
    Student s2 = new Student(80);
    pq.add(s1);
    pq.add(s2);
    
    System.out.println(pq.peek().score); // 输出 80（最小堆，分数最低）
    s2.score = 95; // 修改 s2 的分数，破坏堆结构
    System.out.println(pq.peek().score); // 仍输出 80（堆未调整）
}

解决方案 ：修改元素字段后，先调用 remove(Object o) 移除该元素，再调用 offer(E e) 重新添加，触发上浮/下沉调整。

3. 初始容量的优化建议

若提前知晓队列的预估元素数量，建议在构造 PriorityQueue 时手动指定初始容量（如 new PriorityQueue<>(1000)），避免频繁扩容带来的性能损耗。

总结

1. PriorityQueue 底层基于动态数组+完全二叉堆 实现，默认构建最小堆，通过自定义 Comparator 可灵活实现最大堆或自定义优先级排序。
2. 核心操作（offer()/poll()）依赖上浮（siftUp） 和下沉（siftDown），时间复杂度为 O(log n)，扩容仅在容量不足时触发。
3. 使用时需规避关键坑点：迭代器遍历无序、可变对象修改破坏堆结构、非线程安全，线程安全场景需替换为 PriorityBlockingQueue。
4. 堆顶查看（peek()）是 O(1) 操作，移除指定元素（remove(Object o)）因遍历数组，时间复杂度为 O(n)，需谨慎使用。

8、可视化演示

juejin

9、优先队列的 "优先级" 本质是比较规则

优先级的本质：自定义比较规则

Java 中优先队列（PriorityQueue）的"优先级"并非固定为"数值越大优先级越高"，而是由比较规则决定------无论是简单数值还是复杂对象，只要能通过比较规则判定"谁更优先"，就能实现任意逻辑的优先级队列。核心实现方式有两种：

1. 让元素类实现 Comparable 接口，定义"自然排序"规则；
2. 创建 PriorityQueue 时传入 Comparator 比较器，定义"定制排序"规则（更灵活，推荐）。

场景1：值越小，优先级越高（最小堆）

这是工程中最常用的优先级规则之一（如 Dijkstra 算法、截止日期最早的任务优先），Java 可通过两种方式实现：

方式1：基于 Integer 等基础类型的最小堆（默认）

PriorityQueue 对 Integer、Long 等基础类型包装类的默认排序就是"值越小优先级越高"（最小堆），无需额外配置：

import java.util.PriorityQueue;

public class MinHeapDemo {
    public static void main(String[] args) {
        // 默认最小堆：值越小，优先级越高
        PriorityQueue<Integer> minHeap = new PriorityQueue<>();
        
        // 插入元素
        minHeap.add(5);  // 距离起点5
        minHeap.add(2);  // 距离起点2（优先级更高）
        minHeap.add(8);  // 距离起点8
        minHeap.add(1);  // 距离起点1（优先级最高）
        
        // 按优先级弹出（从小到大）
        System.out.println("按优先级处理（值越小越优先）：");
        while (!minHeap.isEmpty()) {
            System.out.print(minHeap.poll() + " "); // 输出：1 2 5 8
        }
    }
}

方式2：自定义比较器实现最小堆（通用方案）

若需显式定义"值越小优先级越高"（或为自定义类型实现），可通过 Comparator 明确规则：

import java.util.PriorityQueue;
import java.util.Comparator;

public class ExplicitMinHeap {
    public static void main(String[] args) {
        // 显式定义比较器：a < b 时，a 优先级更高（返回负数）
        PriorityQueue<Integer> minHeap = new PriorityQueue<>(
            (a, b) -> Integer.compare(a, b)
        );
        
        minHeap.add(10);
        minHeap.add(3);
        minHeap.add(7);
        
        System.out.println("堆顶（优先级最高）：" + minHeap.peek()); // 输出3
    }
}

场景2：复杂对象的多维度自定义优先级

工程中优先队列常存储复杂对象（如任务、订单、病人信息），优先级需由对象的多个属性组合定义 （如"先按紧急度排序，紧急度相同则按提交时间排序"）。Java 中通过 Comparator 可灵活实现这种多维度规则，这是处理复杂优先级的核心方案。

完整示例：任务调度器（多维度优先级）

步骤1：定义任务类（包含多维度属性）

// 自定义任务类：包含紧急度、提交时间、任务名称三个属性
class Task {
    // 紧急度：1-5，数字越小越紧急
    private int urgency;
    // 提交时间：毫秒时间戳，越小表示提交越早
    private long submitTime;
    // 任务名称
    private String name;

    // 构造方法
    public Task(int urgency, long submitTime, String name) {
        this.urgency = urgency;
        this.submitTime = submitTime;
        this.name = name;
    }

    // Getter方法：供比较器访问属性
    public int getUrgency() {
        return urgency;
    }

    public long getSubmitTime() {
        return submitTime;
    }

    public String getName() {
        return name;
    }

    // 重写toString，方便打印
    @Override
    public String toString() {
        return "紧急度:" + urgency + ", 名称:'" + name + "'";
    }
}

步骤2：定义多维度比较器，实现复杂优先级

优先级规则：

1. 紧急度越小，优先级越高；
2. 紧急度相同时，提交时间越早，优先级越高。

import java.util.PriorityQueue;
import java.util.Comparator;

public class MultiDimensionPriority {
    public static void main(String[] args) throws InterruptedException {
        // 核心：定义多维度比较器
        Comparator<Task> taskComparator = (task1, task2) -> {
            // 第一维度：比较紧急度
            int urgencyCompare = Integer.compare(task1.getUrgency(), task2.getUrgency());
            if (urgencyCompare != 0) {
                // 紧急度不同，直接返回比较结果（小的优先）
                return urgencyCompare;
            }
            // 第二维度：紧急度相同，比较提交时间（早的优先）
            return Long.compare(task1.getSubmitTime(), task2.getSubmitTime());
        };

        // 创建优先队列，传入自定义比较器
        PriorityQueue<Task> taskQueue = new PriorityQueue<>(taskComparator);

        // 模拟插入不同优先级的任务（sleep制造提交时间差）
        taskQueue.add(new Task(2, System.currentTimeMillis(), "发送月度报告"));
        Thread.sleep(100); // 暂停0.1秒，模拟提交时间延迟
        taskQueue.add(new Task(5, System.currentTimeMillis(), "清理临时文件 (不紧急)"));
        Thread.sleep(100);
        taskQueue.add(new Task(1, System.currentTimeMillis(), "修复服务器紧急Bug"));
        Thread.sleep(100);
        taskQueue.add(new Task(2, System.currentTimeMillis(), "回复客户邮件"));

        // 打印队列元素（遍历无序，仅展示内容）
        System.out.println("任务队列（内部存储）：");
        for (Task task : taskQueue) {
            System.out.println("  - " + task);
        }

        // 按优先级处理任务（poll()始终弹出比较器判定的最高优先级元素）
        System.out.println("\n按优先级处理任务：");
        while (!taskQueue.isEmpty()) {
            Task task = taskQueue.poll();
            System.out.println("处理任务：'" + task.getName() + "'（紧急度：" + task.getUrgency() + "）");
        }
    }
}

运行结果

任务队列（内部存储）：
  - 紧急度:1, 名称:'修复服务器紧急Bug'
  - 紧急度:2, 名称:'发送月度报告'
  - 紧急度:2, 名称:'回复客户邮件'
  - 紧急度:5, 名称:'清理临时文件 (不紧急)'

按优先级处理任务：
处理任务：'修复服务器紧急Bug'（紧急度：1）
处理任务：'发送月度报告'（紧急度：2）
处理任务：'回复客户邮件'（紧急度：2）
处理任务：'清理临时文件 (不紧急)'（紧急度：5）

核心扩展：同一类定义多种优先级规则

Comparator 的最大优势是解耦排序逻辑与对象本身，可为同一个类定义多种优先级规则，适配不同业务场景：

public class MultiplePriorityRules {
    public static void main(String[] args) {
        // 规则1：按紧急度升序（小的优先）
        Comparator<Task> byUrgency = (t1, t2) -> Integer.compare(t1.getUrgency(), t2.getUrgency());
        
        // 规则2：按提交时间降序（晚提交的优先，如"最新任务优先"）
        Comparator<Task> bySubmitTimeDesc = (t1, t2) -> Long.compare(t2.getSubmitTime(), t1.getSubmitTime());
        
        // 规则3：按任务名称字母序（辅助排序）
        Comparator<Task> byName = (t1, t2) -> t1.getName().compareTo(t2.getName());

        // 场景1：紧急度优先的队列
        PriorityQueue<Task> urgencyFirstQueue = new PriorityQueue<>(byUrgency);
        
        // 场景2：最新任务优先的队列
        PriorityQueue<Task> latestFirstQueue = new PriorityQueue<>(bySubmitTimeDesc);
    }
}

总结

1. Java 中优先队列的"优先级"本质是比较规则 ，而非固定的数值大小，通过 Comparable 或 Comparator 可定义任意逻辑的优先级。
2. 最小堆（值越小优先级越高）是 PriorityQueue 对基础类型的默认行为，也可通过 Comparator 显式定义，适配自定义类型。
3. 处理复杂对象的多维度优先级时，Comparator 是最优方案：可按"主维度→次维度"的顺序定义比较逻辑，解耦排序规则与对象本身，支持同一类定义多种优先级规则。
4. PriorityQueue 的 poll() 方法始终弹出"比较器判定优先级最高"的元素，这是实现优先级调度的核心逻辑。

10、总结时间复杂度分析

我们来回顾一下不同实现方式的性能对比：

实现方式	插入 (Insert)	提取最高优先级	查看最高优先级
无序数组	O(1)	O(n)	O(n)
有序数组	O(n)	O(1)	O(1)
二叉堆 (Binary Heap)	O(log n)	O(log n)	O(1)

最终结论：

为什么二叉堆是优先队列的最佳选择？ 因为它在插入和提取这两个最核心、最频繁的操作上都达到了 O(log n) 的时间复杂度。这是一种非常理想的平衡。当数据量 n 很大时（例如百万级别），log n 的增长非常缓慢，使得堆的性能远超线性时间 O(n) 的朴素实现。

通过巧妙地利用完全二叉树的结构特性和数组的高效存储，并结合元组等技巧来定义灵活的优先级，二叉堆为我们提供了一个理论和实践上都极为优秀的优先队列解决方案。