COMSOL双温方程二维飞秒激光

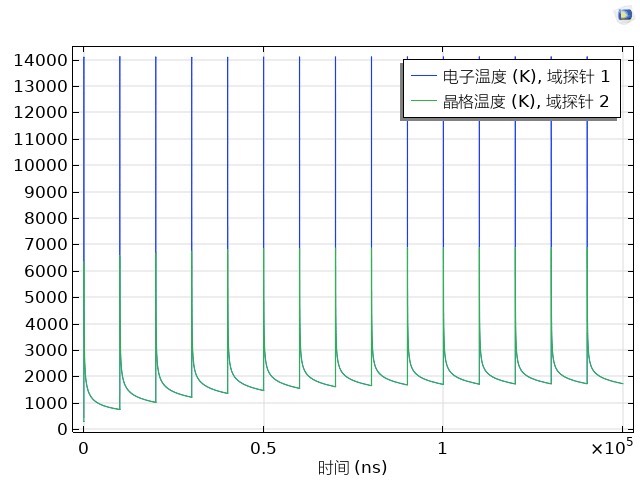
激光加工微纳结构时，飞秒激光与金属的相互作用像一场电子和晶格的"抢椅子游戏"。当超快激光脉冲砸在金箔表面，电子瞬间被加热到上万开尔文，而晶格还躺在室温里发呆------这种温差引发的能量传递戏码，用双温方程才能说清楚。

在COMSOL里搭这个模型，首先得在"弱形式偏微分方程"模块里搞两套方程。电子温度Te和晶格温度Tl各占一个变量，像这样在模型树里并排坐：

matlab 复制代码

% 双温方程核心代码片段
d(T_et, T_et) + (k_e*Tx_e + k_e*Ty_e) - G*(T_l - T_e) - S = 0
d(T_lt, T_lt) + G*(T_e - T_l) = 0

这里的k_e不是常数，而是随电子温度变化的暴脾气参数。我习惯在材料属性里塞个分段函数：

matlab 复制代码

k_e = 353*(T_e/(0.7*T_F))^(-0.44);  // 金的热导率修正公式
T_F = 6.41e4;  // 金的费米温度

这种非线性关系会让求解器时不时闹脾气，建议初始步长压到1e-15秒级别，不然分分钟发散给你看。

边界条件设置要讲究，激光光斑用高斯脉冲描述：

matlab 复制代码

S = (1-R)*P0/(tau*sqrt(pi)) * exp(-(t-2*tau)^2/tau^2) * exp(-(x^2+y^2)/w0^2)

注意这里的脉冲宽度tau取80fs时，时间步长需要小于tau/10。有次偷懒用1fs步长，结果电子温度曲线抖得像心电图的室颤波形。

COMSOL双温方程二维飞秒激光

网格划分更是个技术活。电子热扩散长度约10nm，但激光光斑直径50μm，这意味着中心区域需要加密到1nm级别。COMSOL的极端网格功能这时就派上用场了------在激光作用区域套个直径100nm的圆，应用大小从1nm渐变到100nm的网格，像给模型中心戴了顶极细密的发网。

跑完仿真后，在电子温度云图里能看到有趣的"火山口"现象：中心区域因热电子快速扩散反而温度较低，周围形成环状高温区。这解释了为什么实际加工中烧蚀坑边缘总比中心更整齐------能量沉积的分布方式直接影响材料去除机制。

不过要注意，当晶格温度超过熔点后，双温模型就得打补丁了。这时候在方程里加个相变潜热项：

matlab 复制代码

L * (T_l >= Tm) * derivative(T_l,t)

能让温度曲线在熔点附近出现平台区，更接近真实熔融过程。有次忘记加这项，结果晶格温度像坐火箭直接冲上8000K，比电子还热，整个物理机制都乱套了。

最后说个实用技巧：在2D模型里加个旋转对称轴，能省下80%计算量。但要注意各向异性材料别这么玩------有次研究钛合金忘了这茬，结果各向异性热传导硬是被算成轴对称，误差大到能气哭博士生。