LeetCode第2368题

难度：中等

现有一棵由 n 个节点组成的无向树，节点编号从 0 到 n - 1 ，共有 n - 1 条边。给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges $i$ = $ai, bi$ 表示树中节点 ai 和 bi 之间存在一条边。另给你一个整数数组 restricted 表示受限节点。

在不访问受限节点的前提下，返回你可以从节点 0 到达的最多节点数目。注意，节点 0 不会标记为受限节点。

示例1：

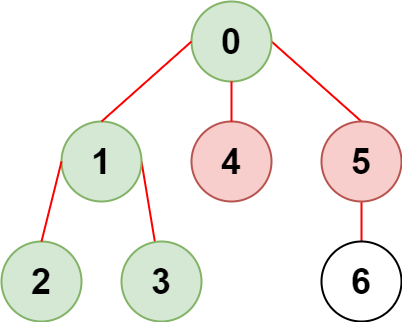
输入：n = 7, edges = $\[0,1$ , $1,2$ , $3,1$ , $4,0$ , $0,5$ , $5,6$ ], restricted = $4,5$

输出：4

解释：上图所示正是这棵树。

在不访问受限节点的前提下，只有节点 $0,1,2,3$ 可以从节点 0 到达。

示例2：

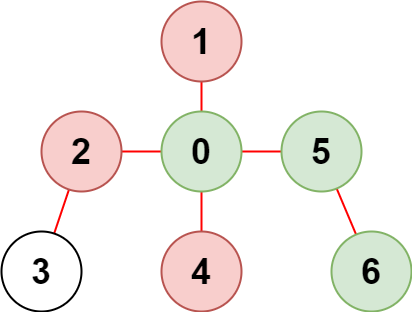
输入：n = 7, edges = $\[0,1$ , $0,2$ , $0,5$ , $0,4$ , $3,2$ , $6,5$ ], restricted = $4,2,1$

输出：3

解释：上图所示正是这棵树。

在不访问受限节点的前提下，只有节点 $0,5,6$ 可以从节点 0 到达。

2 <= n <= 10^5
edges.length == n - 1
edges $i$ .length == 2
0 <= ai, bi < n
ai != bi
edges 表示一棵有效的树
1 <= restricted.length < n
1 <= restricted $i$ < n
restricted 中的所有值互不相同

问题分析

这题说的是在一个有n个节点组成的无向树中，节点0所能到达的节点个数。这里说的无向树其实就是一个无向图，所以这题也就是对图的遍历，注意还要跳过受限的节点。对于图的遍历常见的BFS，DFS和并查集，实际上这题使用这三种方式中的任何一种都可以解决，我们来看一下使用DFS怎么解决的。

从节点0开始递归遍历，查找所有和节点0相连的节点，为了方便查找我们可以使用 n 个集合记录和每一个节点相连的所有节点，类似于图的邻接表，还要使用一个数组来记录受限的节点和已经被访问过的节点，代码如下。

JAVA：

复制代码

public int reachableNodes(int n, int[][] edges, int[] restricted) {
    // n个集合，记录与每一个节点相连的所有节点
    List<Integer>[] lists = new List[n];
    for (int i = 0; i < n; i++)// 初始化集合
        lists[i] = new ArrayList();
    for (int[] edge : edges) {
        // 因为是无向图，所以如果a和b相连，那么b也和a相连。
        lists[edge[0]].add(edge[1]);
        lists[edge[1]].add(edge[0]);
    }
    // 记录受限的节点和已经访问过的节点
    boolean[] isRestricted = new boolean[n];
    for (int restrict : restricted)
        isRestricted[restrict] = true;

    return dfs(0, lists, isRestricted);
}

private int dfs(int start, List<Integer>[] lists, boolean[] isRestricted) {
    if (isRestricted[start])// 如果是受限的节点或者是已经访问过的节点，直接跳过
        return 0;
    isRestricted[start] = true;// 标记为已访问
    int res = 1;
    for (int num : lists[start])// 递归和当前节点相连的所有节点。
        res += dfs(num, lists, isRestricted);
    return res;
}

C++：

复制代码

public:
    int reachableNodes(int n, vector<vector<int>> &edges, vector<int> &restricted) {
        vector<vector<int>> lists(n); // n个集合，记录与每一个节点相连的所有节点
        for (auto &edge: edges) {
            // 因为是无向图，所以如果a和b相连，那么b也和a相连。
            lists[edge[0]].push_back(edge[1]);
            lists[edge[1]].push_back(edge[0]);
        }
        // 记录受限的节点和已经访问过的节点
        vector<bool> isRestricted(n);
        for (int restrict: restricted)
            isRestricted[restrict] = true;
        return dfs(0, lists, isRestricted);
    }

    int dfs(int start, vector<vector<int>> &lists, vector<bool> &isRestricted) {
        if (isRestricted[start])// 如果是受限的节点或者是已经访问过的节点，直接跳过
            return 0;
        isRestricted[start] = true;// 标记为已访问
        int res = 1;
        for (int num: lists[start])// 递归和当前节点相连的所有节点。
            res += dfs(num, lists, isRestricted);
        return res;
    }

Python：

复制代码

def reachableNodes(self, n: int, edges: List[List[int]], restricted: List[int]) -> int:
    def dfs(start: int, lists: List[List[int]], isRestricted: List[bool]):
        if isRestricted[start]:  # 如果是受限的节点或者是已经访问过的节点，直接跳过
            return 0
        isRestricted[start] = True  # 标记为已访问
        res = 1
        for num in lists[start]:  # 递归和当前节点相连的所有节点。
            res += dfs(num, lists, isRestricted)
        return res

    # n个集合，记录与每一个节点相连的所有节点
    lists = [[] for _ in range(n)]
    # 因为是无向图，所以如果a和b相连，那么b也和a相连。
    for edge in edges:
        lists[edge[0]].append(edge[1])
        lists[edge[1]].append(edge[0])
    # 记录受限的节点和已经访问过的节点
    isRestricted = [0] * n
    for restrict in restricted:
        isRestricted[restrict] = True
    return dfs(0, lists, isRestricted)