写在前面
在深度学习中,模型结构决定能力上限,而优化器决定你能否抵达那个上限。它不参与前向计算,也不定义损失函数,却掌控着每一次参数更新的方向与步长------就像登山者在浓雾中选择的下山策略,决定了你能否又快又稳地抵达谷底。
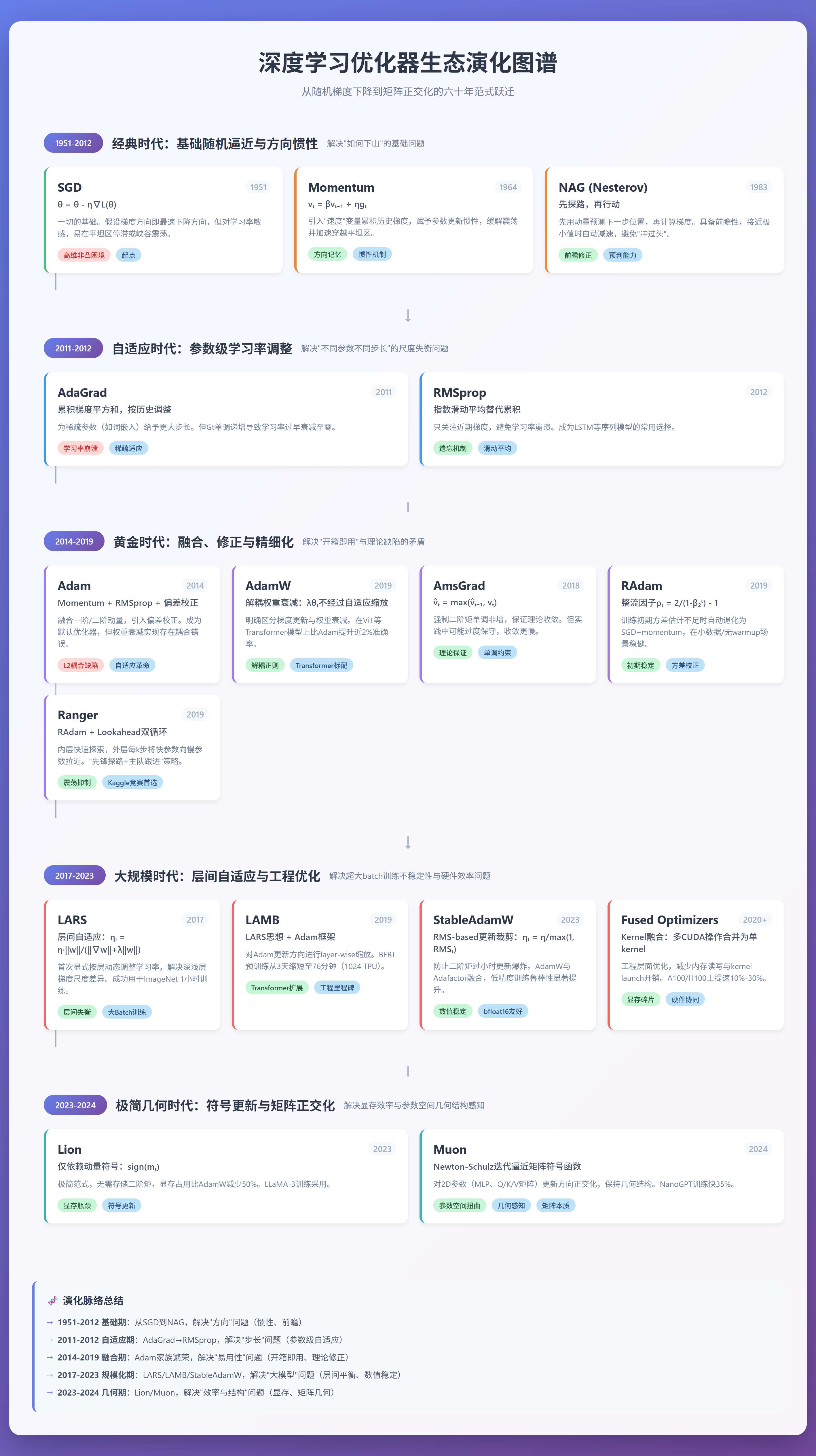
过去几十年,优化器从最朴素的随机梯度下降(SGD),逐步演变为能自适应、可扩展、甚至具备"预判能力"和"几何感知"的智能系统。这一演化并非凭空而来,而是由训练任务的复杂性、模型规模的膨胀以及硬件环境的变化共同驱动。
本文将沿着这条清晰的技术脉络,逐类解析主流优化器的核心思想、数学机制、适用边界,并辅以真实训练场景中的表现,帮助你理解:为什么我们需要这么多优化器?它们究竟解决了什么问题?
❝
本文是一篇综述,旨在梳理各类优化器的发展脉络,但不会涉及过多细节,有兴趣的读者可参阅文末论文或资料,进一步深入学习。
经典时代
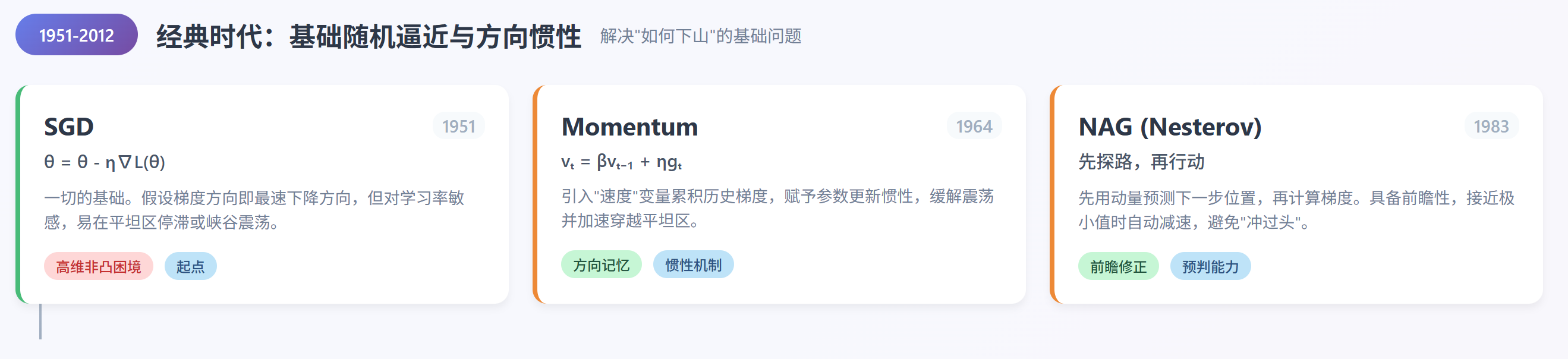
基础随机逼近与方向惯性,解决"如何下山"的基础问题。
SGD
一切始于随机梯度下降(Stochastic Gradient Descent, SGD) [1]。其更新规则极为简洁:
其中 是第 步的模型参数, 是损失函数, 是当前参数处的梯度, 是全局学习率。
SGD 的核心假设是:梯度方向就是下降最快的方向。
然而在高维非凸损失 landscape 中,这一假设常常失效。SGD 容易在平坦区域停滞(梯度接近零但远离最优解),或在狭窄峡谷中左右震荡(不同维度曲率差异大)。更重要的是,它对学习率极其敏感:太大则发散,太小则收敛极慢。
尽管如此,SGD 仍是所有现代优化器的起点。2012 年 AlexNet 的成功,正是基于 SGD 配合动量项,首次证明了深度卷积网络可在大规模数据上有效训练。
Momentum
为缓解震荡并加速穿越平坦区域,Momentum(动量) [2] 被引入。其核心思想是引入一个"速度"变量 ,累积历史梯度信息:
这里 是动量系数(通常取 0.9),控制历史信息的衰减速度。
直观上,这相当于给参数更新赋予"惯性"------即使当前梯度很小,只要过去方向一致,更新仍会继续推进。这种机制显著提升了在 ResNet、VGG 等 CNN 上的训练稳定性。
NAG
然而 Momentum 仍存在一个缺陷:它总是在当前位置计算梯度,再叠加历史动量,可能导致"冲过头"。Nesterov Accelerated Gradient (NAG) [3] 对此进行了关键改进:先用动量预测下一步位置 ,再在此处计算梯度:
这种"先探路再行动"的策略,使算法具备前瞻性,在接近极小值时能自动减速。在 RNN 或强化学习等对初始阶段敏感的任务中,NAG 常比标准 Momentum 表现更优。PyTorch 等各类训练框架均支持通过 nesterov=True 启用该模式。
较有代表性的优化器是 NAdam [21], 它代表了优化器设计中一个重要的融合思路:将加速机制(NAG)与自适应机制(Adam)统一于同一框架,为后续研究提供了理论桥梁。
自适应时代
参数级学习率调整,解决"不同参数不同步长"的尺度失衡问题。

AdaGrad
如果说 Momentum 解决了"方向记忆"问题,那么自适应学习率方法则致力于解决"尺度失衡"问题。
2011年提出的 AdaGrad [4] 观察到:在稀疏数据(如 NLP 中的词嵌入)中,某些参数极少更新,应给予更大步长;而频繁更新的参数则需谨慎。它为每个参数 维护一个累积梯度平方和 ,并按 缩放学习率。
虽然这一思想极具启发性,但 单调递增导致学习率过早衰减至零,使得 AdaGrad 在非凸问题(如深度神经网络)中表现不佳。
RMSprop
2012年提出的RMSprop [5] 对此进行了修正,用指数滑动平均替代累积:
其中 , 是数值稳定项(通常 )。
通过只关注近期梯度,RMSprop 避免了学习率崩溃,成为 LSTM 等序列模型的常用选择。
黄金时代
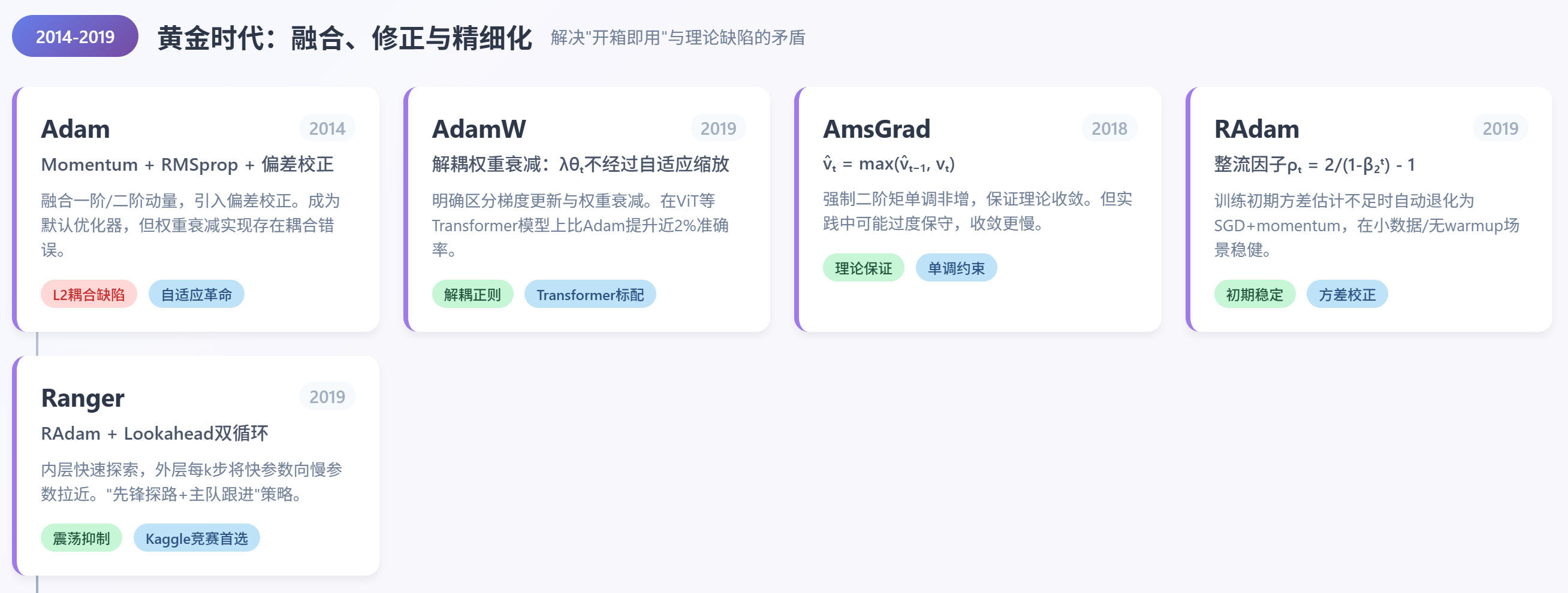
融合、修正与精细化,解决"开箱即用"与理论缺陷的矛盾。
Adam
真正引爆自适应优化器普及的是2014年提出的 Adam [6],它将 Momentum 与 RMSprop 融为一体,并加入偏差校正:
其中 是一阶矩(动量), 是二阶矩(梯度平方的滑动平均), 通常取 0.9 和 0.999。偏差校正项 解决了初期估计偏低的问题。
Adam 因其"开箱即用"的特性,迅速成为默认优化器。然而,它在实现权重衰减(weight decay)时犯了一个隐蔽错误:将 L2 正则项直接加到梯度中,导致自适应学习率与权重衰减耦合,削弱了正则效果。
AdamW
这一问题直到2019年提出的 AdamW [9]才被彻底纠正。AdamW 明确区分了"梯度更新"与"权重衰减"两个操作:
其中 是权重衰减系数。注意, 不经过自适应缩放,而是直接作用于参数本身。
这一看似微小的改动,在 Transformer 这类模型中带来显著提升:在 ImageNet 上训练 ViT 时,AdamW 比 Adam 高出近 2% 的 top-1 准确率。
除了 AdamW,在 Adam 的基础上,还有很多变体试图解决其理论或实践缺陷。
AmsGrad
2018年提出的AmsGrad [7] 指出 Adam 的二阶矩估计 可能随时间减小,导致学习率回升,破坏收敛性。为此,AmsGrad 强制使用历史最大值:
理论上这保证了学习率单调非增,但在实际训练中(尤其是带 warmup 的 Transformer),AmsGrad 很少优于 AdamW,且可能因过度保守而收敛更慢。
RAdam
相比之下,2019年提出的 RAdam [8] 关注的是 Adam 在训练初期因方差估计不足导致的不稳定问题。它引入一个"整流因子" ,当有效样本数较少时,自动抑制自适应学习率:
若 > 4, 则使用自适应更新;否则退化为 SGD with momentum。
这一机制使 RAdam 在小数据集(如医疗图像分类)、无 warmup 训练或超参搜索中表现稳健。
Ranger
而将 RAdam 与 Lookahead [10] 结合形成的 Ranger [18] 优化器,在小数据任务中表现出更强的训练稳定性,曾被 Kaggle 竞赛社区广泛采用。
其中的 Lookahead 提出双循环更新:内层(如 RAdam)快速探索,外层每 步(通常 5~6)将快参数向慢参数拉近:
其中 通常取 0.5。
这种"先锋探路+主队跟进"的策略显著提升了稳定性,尤其在 loss 曲线震荡较大的任务中。
大规模训练时代
层间自适应与工程优化,解决超大batch训练不稳定性与硬件效率问题。

随着模型规模突破十亿参数,新的挑战浮现:超大 batch size 下的训练不稳定性。
传统优化器(如 SGD、Adam)对所有参数使用统一或参数级自适应的学习率,未显式考虑不同网络层之间梯度尺度的巨大差异。
实践中,浅层(如底层卷积层)与深层(如顶层注意力头)的梯度范数常相差几个数量级,导致浅层更新不足。
LARS
2017年提出的 LARS [11](Layer-wise Adaptive Rate Scaling)首次提出一种显式的、按层动态调整学习率的机制,通过将每层的学习率与权重范数和梯度范数的比值成比例,有效缓解了这一问题,尤其适用于大 batch 训练。其更新形式为:
其中 是第 层参数, 为解耦权重衰减项。
LARS 成功用于 ResNet-50 在 ImageNet 上的 1 小时训练(batch size=32k)。然而,LARS 依赖 Momentum,无法直接用于含 LayerNorm 的 Transformer。
LAMB
为此,2019年提出的 LAMB [12] 将 LARS 思想嫁接到 Adam 上,对 Adam 的更新方向 进行 layer-wise 缩放:
这一设计使 BERT 预训练时间从 3 天大幅缩短至 76 分钟(在 1024 TPU v3 芯片上),成为大模型工程化的里程碑。
StableAdamW
与此同时,针对大模型训练中因二阶矩估计过小而导致更新步长剧烈波动的稳定性问题,StableAdamW [19,20] 于2023年被提出。 它并非 LAMB 的延伸,而是 AdamW 与 Adafactor 的融合:在保留 AdamW 解耦权重衰减的基础上,引入基于 RMS 的 per-tensor 更新裁剪机制。
具体而言,StableAdamW 对每个参数张量独立计算其梯度的均方根(RMS):
其中 是梯度平方的指数移动平均(EMA),即 。该 RMS 值反映了当前梯度信号的强度。
然后,动态缩放学习率定义为:
该机制有效防止了因 过小而导致的更新爆炸,在低精度训练(如 bfloat16)或使用极高学习率时显著提升鲁棒性。
Fused Optimizers
在工程层面,也产生了 Fused Optimizers 融合优化器的思路,也即:通过将多个 CUDA 操作(如 Adam 更新中的乘加、除法、weight decay)融合为单个 kernel,显著减少内存读写与 kernel launch 开销。
注意,"融合"并非特指,而是一类优化器的思路,比如 FusedAdam。
在 A100/H100 上,FusedAdam 可提速 10%~30%,同时降低显存碎片。NVIDIA Apex 库和 PyTorch 2.0 的 torch.compile 均支持此类优化。虽然不改变算法逻辑,但 Fused 实现在大规模训练中已成为标配[16]。
极简几何时代
符号更新与矩阵正交化,解决显存效率与参数空间几何结构感知。

Lion
2023年,Lion [13](Evolved Sign Momentum)提出一种极简高效的新范式。它仅依赖动量的符号(sign)进行更新:
由于无需存储二阶矩 ,Lion 的显存占用比 AdamW 减少近 50%,同时在 LLaMA、PaLM 等大模型上达到相当甚至更优的性能。Meta 已在 LLaMA-3 训练中采用 Lion,标志着优化器进入"极简高效"的新阶段。
Muon
最近登场的 Muon [14](MomentUm Orthogonalized by Newton-Schulz),由 Keller Jordan 等人于 2024 年提出。Muon 的核心洞察是:对于具有矩阵结构的参数(如 MLP 权重、Q/K/V 投影矩阵),其更新方向不应被少数奇异方向主导,而应尽可能"各向同性"------即保持更新方向的正交性,避免参数空间扭曲。
为此,Muon 先计算带动量的梯度矩阵 ,然后通过 Newton-Schulz 迭代高效逼近其"矩阵符号函数"(matrix sign function),该函数在数学上等价于将 投影到最近的半正交矩阵(即满足 形式的矩阵,其中 为正交基)。最终更新方向即为这一正交化后的矩阵。这种操作保留了梯度的主要方向信息,同时抑制了病态条件数带来的数值不稳定。
为理解这一设计的意义,可以想象你要调整一张照片的"艺术风格":
- 传统优化器(如 AdamW)像是逐个像素调节亮度或饱和度,完全不考虑整张图的构图、人物朝向或背景透视关系;
- Muon 则先分析整张图的"主结构方向"(比如人物主体朝左、地平线轻微倾斜),然后对这些整体几何特征进行协调微调,从而在改变风格的同时保持画面结构的合理性。
显然,后者更符合人类对"有意义修改"的直觉。类似地,神经网络中的权重矩阵编码了输入与输出之间的线性映射结构,直接对其做正交化更新,能更好地维持这种结构的稳定性。
更为详尽的数学公式推导,也可以参考文章"Muon优化器赏析:从向量到矩阵的本质跨越"[15]。
实验证明,在 NanoGPT 的 speedrunning 训练任务中,使用 Muon 优化隐藏层可比 AdamW 快约 35% 达到相同验证损失 ;在 CIFAR-10 上训练小型 Transformer,总训练成本从 3.3 A100-秒降至 2.6 A100-秒 [14,17]。值得注意的是,Muon 仅用于隐藏层的 2D 参数(如线性投影权重),而 embedding、layer norm、bias 等标量或向量参数仍用 AdamW 优化。这一"混合策略"反映了对参数几何结构的深刻理解:向量与矩阵的本质差异,值得不同的优化方式。
总结
综上所述,优化器的演化是一条由实际训练问题驱动的清晰技术脉络:始于 SGD 的基础随机逼近[1],通过 Momentum 与 NAG 引入方向惯性以缓解震荡并加速收敛[2,3];随后,AdaGrad 首次提出参数级自适应学习率,专为稀疏数据设计[4],但因学习率过早衰减而受限;RMSprop 改用滑动平均机制,有效避免了这一缺陷,成为序列模型训练的重要工具[5];继而 Adam 融合一阶与二阶动量,并引入偏差校正,掀起自适应优化的革命,迅速成为默认选择[6];然而其权重衰减实现存在耦合问题,直到 AdamW 明确解耦梯度更新与正则项,才在 Transformer 类模型中释放全部潜力[9];后来的 StableAdamW 则进一步引入更新量裁剪机制,显著提升大模型训练的稳定性[19,20];与此同时,其他变体如 AmsGrad 尝试通过约束二阶矩单调性来保证理论收敛性[7],而 RAdam 则通过整流机制解决 Adam 初期不稳定问题,在小数据或无 warmup 场景中表现稳健[8];将 RAdam 与 Lookahead 结合形成的 Ranger 优化器,在小数据任务中表现出更强的训练稳定性,曾被 Kaggle 竞赛社区广泛采用[10,18];面对超大 batch 训练挑战,LARS 首次引入层间自适应缩放策略[11],其思想被 LAMB 成功扩展至 Adam 框架,在 1024 TPU v3 芯片上将 BERT 预训练时间从 3 天大幅缩短至 76 分钟[12];工程层面,Fused Optimizers (如 FusedAdam)通过 kernel 融合显著提升吞吐与显存效率,已成为大规模训练标配[16];2023 年,Lion 以极简符号更新实现更低显存占用与更高训练效率,标志着向"极致高效"迈进[13];最新提出的 Muon 则从矩阵几何结构出发,对隐藏层权重进行正交化更新,首次将"参数类型差异"(向量 vs. 矩阵)纳入优化设计,在 NanoGPT 与 CIFAR-10 上验证了其加速能力[14,17]。
没有"最好"的优化器,只有"最适合"当前任务、模型结构与硬件环境的策略。理解这一完整演化脉络,不仅能帮你做出更明智的工程选择,更能洞察深度学习系统设计的底层逻辑------即:优化不仅是数学,更是对参数空间几何、计算约束与任务语义的综合建模。
最后再来回顾下发展脉络:

参考文献
1\] Robbins, H., \& Monro, S. (1951). A stochastic approximation method. *Annals of Mathematical Statistics*. \[2\] Polyak, B. T. (1964). Some methods of speeding up the convergence of iteration methods. *USSR Computational Mathematics and Mathematical Physics*. \[3\] Nesterov, Y. (1983). A method for unconstrained convex minimization problem with the rate of convergence . *Doklady AN USSR*. \[4\] Duchi, J., Hazan, E., \& Singer, Y. (2011). Adaptive subgradient methods for online learning and stochastic optimization. *Journal of Machine Learning Research*. \[5\] Tieleman, T., \& Hinton, G. (2012). Lecture 6.5---RMSProp: Divide the gradient by a running average of its recent magnitude. *COURSERA: Neural Networks for Machine Learning*. \[6\] Kingma, D. P., \& Ba, J. (2014). Adam: A method for stochastic optimization. *arXiv:1412.6980* \[7\] Reddi, S. J., Kale, S., \& Kumar, S. (2018). On the convergence of Adam and beyond. *arXiv:1904.09237* \[8\] Liu, L., et al. (2019). On the variance of the adaptive learning rate and beyond. *arXiv:1908.03265* \[9\] Loshchilov, I., \& Hutter, F. (2019). Decoupled weight decay regularization. *arXiv:1711.05101*. \[10\] Zhang, M., Lucas, J., Ba, J., \& Hinton, G. E. (2019). Lookahead optimizer: k steps forward, 1 step back. *arXiv:1907.08610*. \[11\] You, Y., et al. (2017). Large batch training of convolutional networks. *arXiv:1708.03888*. \[12\] You, Y., et al. (2019). Reducing BERT pre-training time from 3 days to 76 minutes. *arXiv:1904.00962*. \[13\] Chen, X., et al. (2023). Symbolic discovery of optimization algorithms. *arXiv:2302.06675*. \[14\] Jordan, K., et al. (2024). Muon: An optimizer for hidden layers in neural networks. Blog post. *https://kellerjordan.github.io/posts/muon/* \[15\] 苏剑林. (2024). Muon优化器赏析:从向量到矩阵的本质跨越. *科学空间* . *https://kexue.fm/archives/10592* \[16\] PyTorch Documentation: Optimizers. *https://pytorch.org/docs/stable/optim.html* \[17\] GitHub - KellerJordan/Muon. *https://github.com/KellerJordan/Muon* \[18\] Wright, L. (2019). Ranger-Deep-Learning-Optimizer \[Computer software\]. GitHub. *https://github.com/lessw2020/Ranger-Deep-Learning-Optimizer* \[19\] Wortsman, M., Dettmers, T., Zettlemoyer, L., Morcos, A., Farhadi, A., \& Schmidt, L. (2023). Stable and low-precision training for large-scale vision-language models. *arXiv:2304.13013*. \[20\] Warner, B. (2024). StableAdamW \[Computer software\]. *https://optimi.benjaminwarner.dev/optimizers/stableadamw/* \[21\] Dozat, T. (2016). Incorporating Nesterov Momentum into Adam. *Stanford University Technical Report.*