如何计算时间复杂度与空间复杂度

我们在做题目的时候，可能会看到各种各样的解题方法，那我们如何去衡量这些解题方法的好和坏？今天要学的时间复杂度和空间复杂度，就是用来衡量你算法好坏的标准

1. 时间复杂度

在计算机科学中，时间复杂度是一个函数 T（n）, 这个 T(n) 函数式定量描述了程序中语句的执行次数, 映射到我们生活中，它的意思就是我完成一件事情所花费的时间

cpp 复制代码

void fun(int N)
{
    int count = 0;
    for(int i = 0; i < N; i++)
    {
        for(int j = 0; j < N; j++)
        {
        ++count; // 执行次数是 n*n，也就是 n^2
        }
    }
     for(int k = 0; k < 2 * N; k++)
    {
    ++count; // 执?次数是 2*n
    } 
    int M = 10;
    while(M--)
    {
        ++count; // 执?次数 10
    }
 }

在这个函数中fun 函数 ++count 语句的总执行次数：T (N) = N^2 + 2 × N + 10

由于 N ^ 2 是对执行次数影响最大的，所以我们在描述时间复杂度时会认为 O(n ^ 2)

如果你是第一次接触这个概念，你可能会说那我创建 count 变量、创建M变量这不需要时间吗？为什么我不去计算这两个操作所花费的时间呢?

其实是是因为我们的计算机是一个很强大的工具，它每秒呢能执行10^7到10^8次循环,而创建键 count 变量和 M 变量对计算机来说所需要消耗的时间太少了，所以我们并不去考虑它所消耗的时间

1.2 计算规则

1. 在 T(N) 只保留低阶项，去掉低阶项

2.如果最高项存在且不是 1 ，则去掉常数系数

3. T（N) 中如果只有常数项，则认为时间复杂度为 O(1)

如果我们遇到递归，它时间复杂度的计算方法是每一次运行的时间复杂度×运行的次数

1.3 案例分析

cpp 复制代码

//从a[] 中找到 goal ，n 代表 a 数组的元素个数 
//如果找到就返回下标，否则返回 -1 
int find(int a[], int goal, int n) //
{
	for(int i = 0; i < n; i++)
	{
		if(a[i] == goal)
		{
			return i;
		}
	}
	return -1;
	
}

在这个 find 函数中最好的情况 for 循环需要执行一次，最坏的情况需要执行 n 次，平均需要执行 n / 2 次，由于计算规则需要去掉次数最高项的系数，所以时间复杂度为O(n)

2. 空间复杂度

空间复杂度的意思是一段程序需要运行起来，需要向电脑申请多大空间的内存

那我们可以想到，对于我们一个程序来说，最占空间的是什么？其实是数组吧，因为我们正常的去创建变量它所造成的空间开销并不会很大

cpp 复制代码

#define N 10
int main()
{
	int arr[N] = {42, 15, 93, 6, 28, 71, 55, 39, 84, 5 };
	int n = N;
	
	for(int i = 0; i < n - 1; i++)
	{
		for(int j = 0; j < n - 1 - i; j++)
		{
			if(arr[j] > arr[j + 1])
			{
				int temp = arr[j];
				arr[j] = arr[j + 1];
				arr[j + 1] = temp; 
			}
		}
	}
	
	for(int i = 0; i < n; i++)
	{
		cout << arr[i] << endl;
	}
	return 0;
}

大家可以看，这段代代码的目的是实现冒泡排序，无论你看不看得懂都没有关系，你只需要知道这个代码的功能是在 for 循环这个位置实现的

从哪里去计算我们这段代码的空间复杂度呢？就是在创建数组这个位置，就是int arr[n]

3. 常见复杂度增长关系

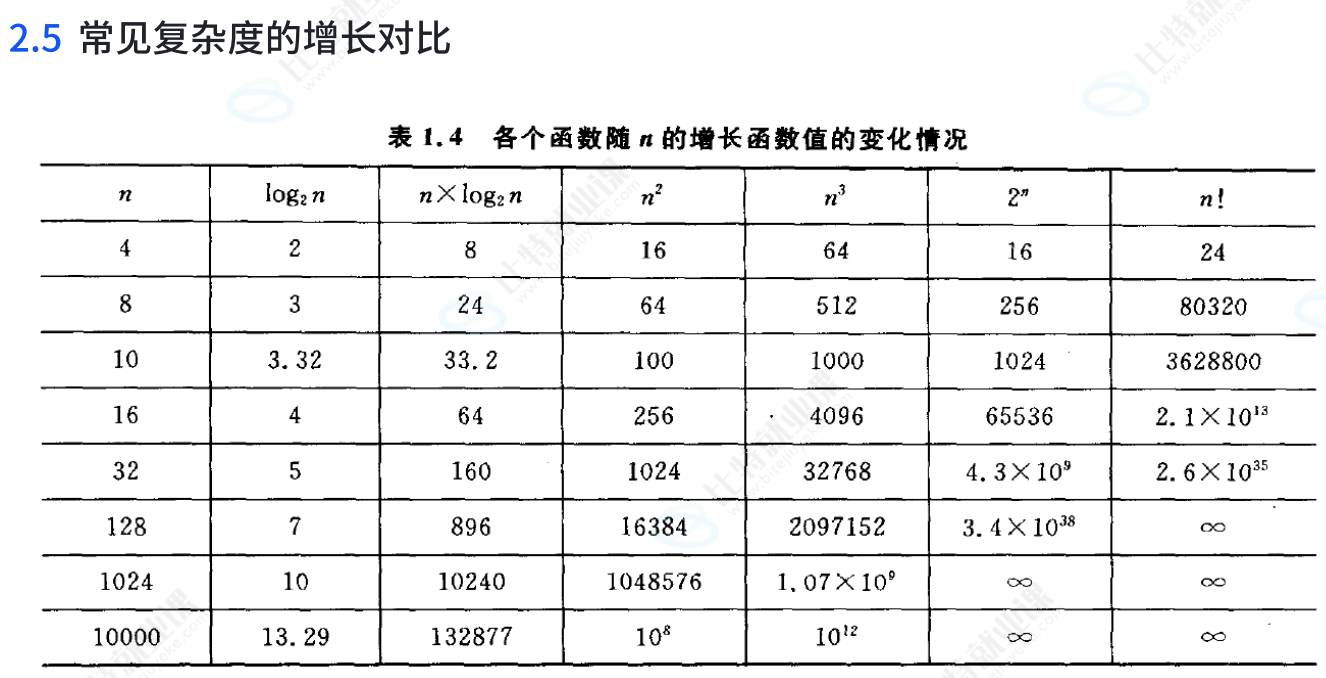
各种常见的时间复杂度的大小对比：

O(1) < O(logN) < O(N) < O(NlNlogN) < O(N ^ 2 ) < O(N ^ 3 ) < O(2 ^ n ) <N O(n!)

在大多数的算法竞赛中，C++它都有着1~2秒的时间限制，这意味着我们的程序执行次数要控在10^7~10^8之间

空间限制在128MB～256MB之间，可以创建3×10^7大小的int类型的数组，或者是5000×5000的二维数组，一般情况下都是够用的

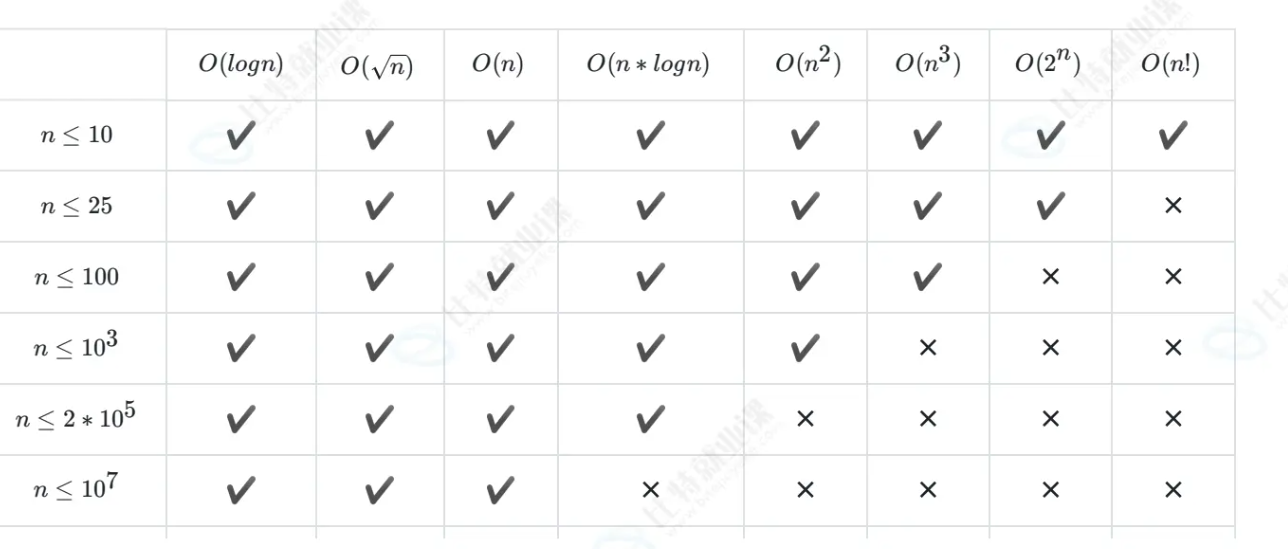
这个表表格是用来计算空间复杂度的表格，首先你需要识别出来你的算法的空间复杂度是属于其中的哪个类型，再去看你的N是多大，以此判断你会不会超时