B-02. Shared Memory 深度优化：从 Bank Conflict 到 Tensor Core Swizzling

在上一章，我们利用向量化和 TMA 榨干了 HBM3e 的 8TB/s 带宽。数据终于跨越了漫长的 PCIe 和 Crossbar，抵达了计算核心的最后一道防线------Shared Memory (SMEM)

Shared Memory 是 GPU 上唯一可编程的高速缓存（L1 Cache 级别）。它的延迟极低（约 20-30 cycles），带宽极高（TB/s 级别）。对于 GEMM、Convolution 这种计算密集型算子，Shared Memory 是用来做 Tiling（分块）和 Data Reuse（数据复用）的绝对核心。

但是，硬件标称的高带宽并不代表你能拿到高带宽。Shared Memory 并非一块连续平坦的内存体，而是由 32 个独立的存储体（Bank） 组成的阵列。如果你不懂这里的"交通规则"，一次错误的访问模式就能让带宽瞬间暴跌至理论值的 1/32，让你的强大的 Tensor Core 因为"喂不饱"而处于饥饿状态。

本章我们将深入 Shared Memory 的微架构，从最基础的 Bank Conflict 开始，一步步掌握为了适配现代 Tensor Core 而必须采用的高级 Swizzling 技术。

1. 物理层：32 Banks 的交通规则

为什么是 32 个 Bank？这并不是巧合，而是为了匹配 CUDA 的基本执行单元 ------ Warp Size (32)。

理想情况下，GPU 设计者希望 Warp 中的 32 个线程能在一个时钟周期内同时完成数据的读取或写入。为了实现这一点，硬件将 Shared Memory 切割成了 32 个独立的通道（Bank），每个 Bank 每个周期可以服务一个 32-bit 的请求。

想象一下线性地址空间（以 float 为单位）：

Row 0:  [  0][  1][  2]...[ 31]
Row 1:  [ 32][ 33][ 34]...[ 63]
Row 2:  [ 64][ 65][ 66]...[ 95]
...
Row 31: [992][993][994]...[1023]

1.1 地址映射逻辑

Shared Memory 的地址是按照 4 字节 (32-bit) 为单位，依次条带化（Striped）映射到 Bank 0 ~ Bank 31 的。

• Word 0 (地址 0-3) → \rightarrow → Bank 0
• Word 1 (地址 4-7) → \rightarrow → Bank 1
• ...
• Word 31 → \rightarrow → Bank 31
• Word 32 → \rightarrow → 回到 Bank 0

这就构成了一个简单的模运算关系： Bank ID = ( Address / 4 ) % 32 \text{Bank ID} = (\text{Address} / 4) \% 32 Bank ID=(Address/4)%32。

1.2 两种"和谐"状态

在讨论冲突之前，我们先看看什么是"好"的访问：

1. 全并行（Conflict-Free）：Warp 内 32 个线程，恰好访问 32 个不同的 Bank。这就像 32 辆车分别走 32 个不同的收费口，全速通过。

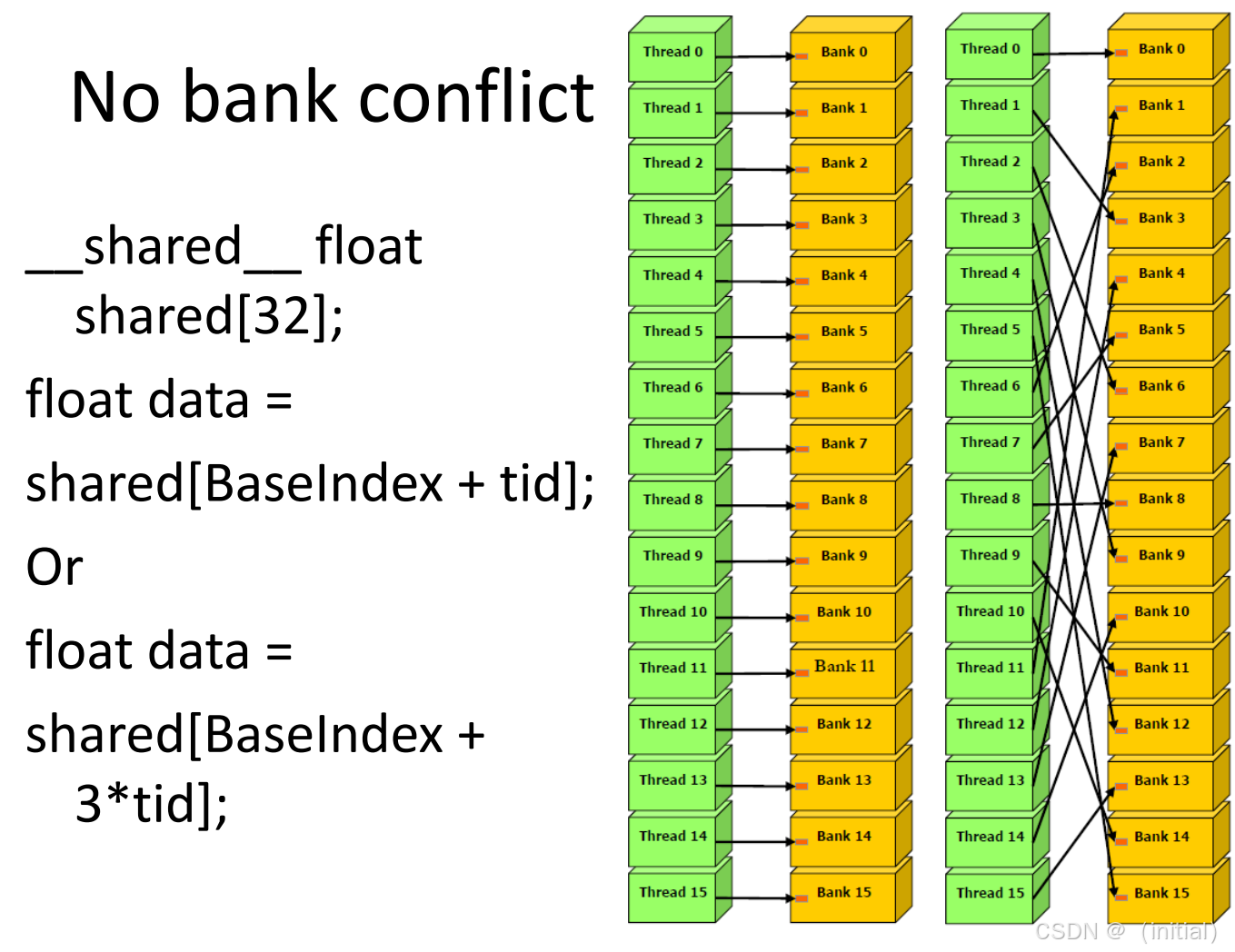
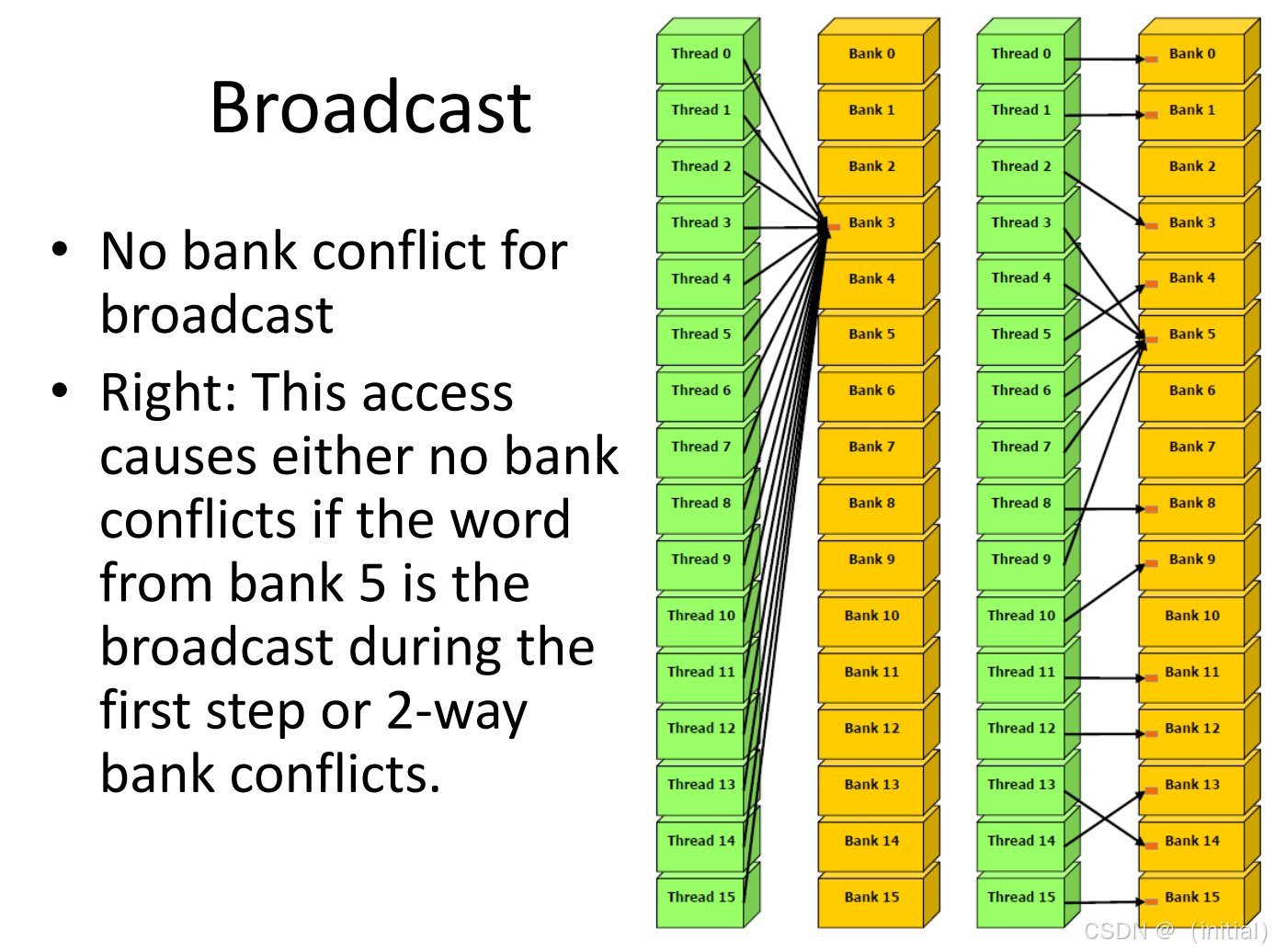
2. 广播（Broadcast） ：Warp 内多个（或所有）线程访问同一个 Bank 的同一个地址 。硬件有特殊的广播电路，这不仅没有冲突，反而是最快的。
   

---

2. 冲突机制：当 32 辆车都要过独木桥

2.1 什么是 Bank Conflict？

当 Warp 内的多个线程试图访问同一个 Bank 的不同地址时，Bank Conflict 就发生了。

想象一下，Bank 0 就像一个单窗口的柜台。如果线程 0 要买 Bank 0 的"苹果"，线程 1 要买 Bank 0 的"香蕉"，柜台无法同时服务。

2.2 硬件行为：指令重播 (Replay)

硬件处理冲突的方式非常简单粗暴：排队。

• 2-way Conflict ：如果有 2 个线程冲突，硬件会将请求拆分为 2 次发射。带宽减半。

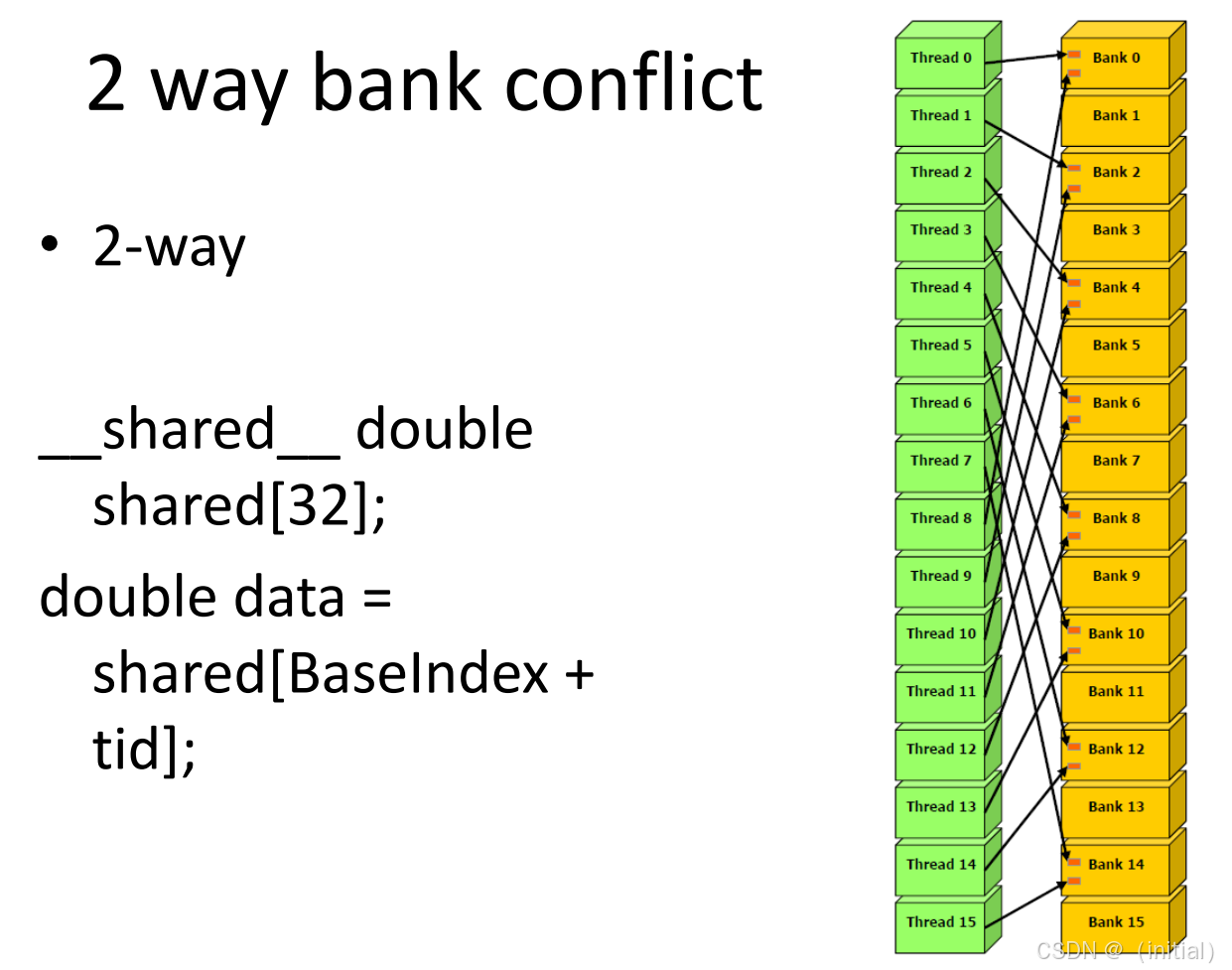
• 8-way Conflict ：如果有 8个线程冲突，硬件会将请求拆分为 8次发射。带宽1/8。
  

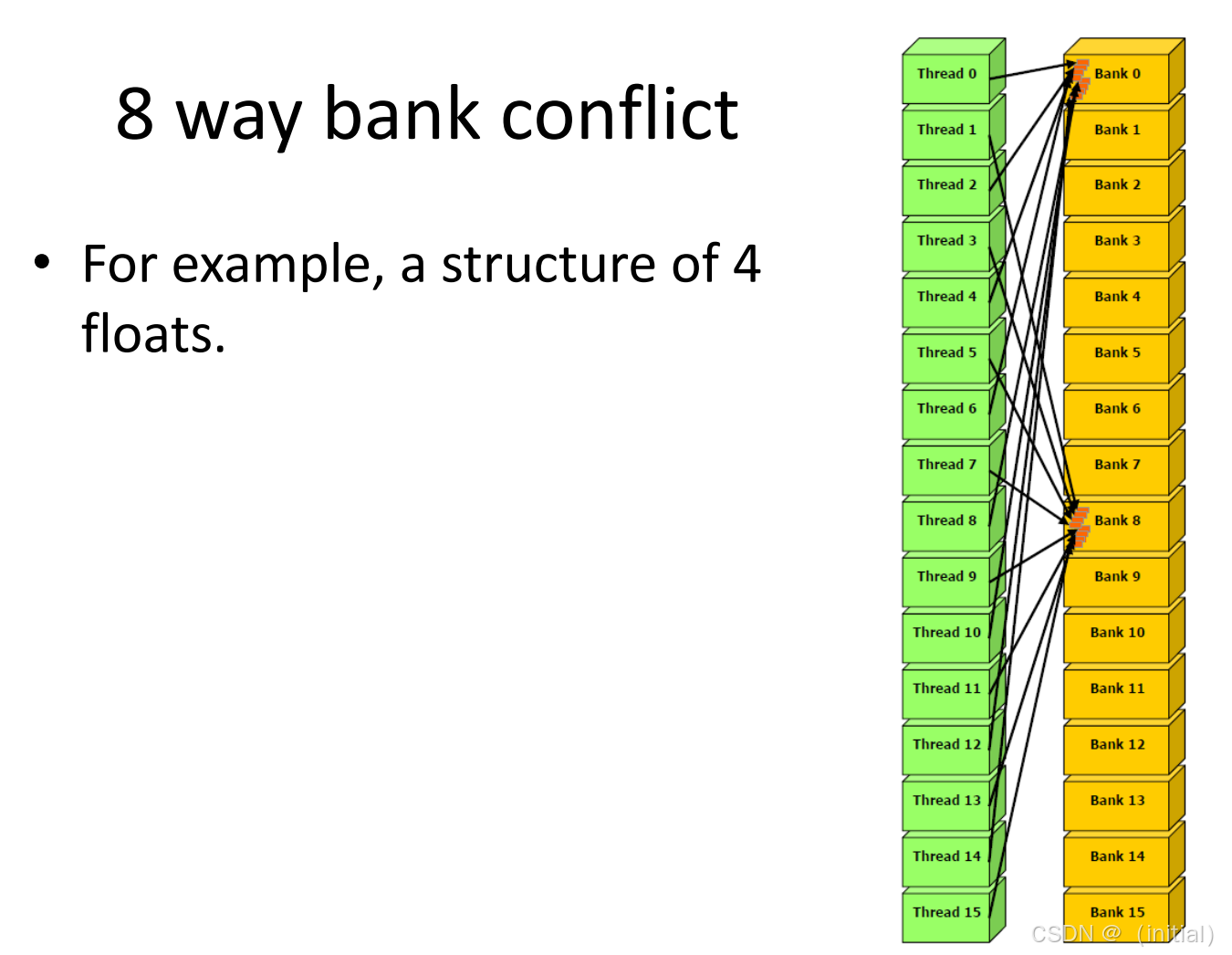
• 32-way Conflict：最坏情况。32 个线程全部落在 Bank 0 的不同地址上。硬件必须连续发射 32 次指令才能完成服务。

  • 后果 ：这条指令的延迟增加了 32 倍，有效带宽降为 1/32。

2.3 典型案发现场：矩阵列访问

这是最容易踩坑的场景。假设我们在 Shared Memory 中存储了一个 32 × 32 32 \times 32 32×32 的 float 矩阵，按行优先（Row-Major）存储。

• 按行读取 ：线程 tid 读取 data[row][tid]。每个线程访问相邻的 float，分别落入 Bank 0~31。无冲突。

  data[row][tid]

  假设 row = 0：

  Thread 0  -> data[0][0]  -> addr 0   -> Bank 0
  Thread 1  -> data[0][1]  -> addr 1   -> Bank 1
  Thread 2  -> data[0][2]  -> addr 2   -> Bank 2
  ...
  Thread 31 -> data[0][31] -> addr 31  -> Bank 31

  图示（完美分散）

  Bank:   0   1   2   3   4  ...  31
  Thread: 0   1   2   3   4  ...  31

• 按列读取 ：线程 tid 读取 data[tid][col]。

  • 线程 0 读取 Row 0, Col 0 → \rightarrow → Bank 0
  • 线程 1 读取 Row 1, Col 0。注意，一行有 32 个 float，正好跨越一轮 Bank。所以 Row 1, Col 0 依然落在 Bank 0！
  • ...
  • 结果 ：32 个线程全部扎堆在 Bank 0。32-way Conflict。

  访问方式

  data[tid][col]

  假设 col = 0

  每个线程访问的地址

  Thread 0  -> data[0][0]  -> addr 0
  Thread 1  -> data[1][0]  -> addr 32
  Thread 2  -> data[2][0]  -> addr 64
  Thread 3  -> data[3][0]  -> addr 96
  ...
  Thread 31 -> data[31][0] -> addr 992

  Bank 映射

  addr 0   % 32 = 0
  addr 32  % 32 = 0
  addr 64  % 32 = 0
  addr 96  % 32 = 0
  ...
  addr 992 % 32 = 0

               Bank 0
     ┌───────────────────────────┐
     │ Thread 0                  │
     │ Thread 1                  │
     │ Thread 2                  │
     │ Thread 3                  │
     │ ...                       │
     │ Thread 31                 │
     └───────────────────────────┘
  
  Bank 1  Bank 2  Bank 3  ... Bank 31
   空      空      空           空

  或者更直观一点：

  Thread:   0   1   2   3   4   ... 31
  Address:  0  32  64  96 128  ... 992
  Bank:     0   0   0   0   0   ...  0

---

3. 经典解法：Padding (空间换时间)

根因只有一句话：

行跨度 = 32 float = Bank 数量 → Bank 映射周期性重合

所以我们要做的只有一件事：

让"行跨度 ≠ 32"

3.1 解决方案：人为制造"错位"------Padding 一列

原始矩阵

float data[32][32];

改造后（关键）

float data[32][33];   // 每行多 1 个 float

• 额外这一列：

  • 不参与计算
  • 只用于 破坏 Bank 对齐

---

3.2 Padding 后的线性布局

Row 0:  [  0][  1][  2]...[ 31][ 32]
Row 1:  [ 33][ 34][ 35]...[ 64][ 65]
Row 2:  [ 66][ 67][ 68]...[ 97][ 98]
...

👉 每一行的起始地址，都比上一行多 33

---

3.3 重新走一遍"案发现场"：按列访问

访问方式（不变）

data[tid][col]   // 假设 col = 0

---

每个线程访问的地址

Thread 0  -> data[0][0]  -> addr 0
Thread 1  -> data[1][0]  -> addr 33
Thread 2  -> data[2][0]  -> addr 66
Thread 3  -> data[3][0]  -> addr 99
...
Thread 31 -> data[31][0] -> addr 1023

---

3.4 Bank 映射（关键反转）

addr % 32：

Thread 0 :  0 % 32 = 0
Thread 1 : 33 % 32 = 1
Thread 2 : 66 % 32 = 2
Thread 3 : 99 % 32 = 3
...
Thread 31:1023 % 32 = 31

---

3.5 Padding 后的"现场复原图"

Bank:   0   1   2   3   4  ...  31
Thread: 0   1   2   3   4  ...  31

🎉 再次完美分散 → 0 Bank Conflict

---

3.6 对比总结（事故前 vs 修复后）

场景	行跨度	Bank 冲突
32×32	32	❌ 32-way conflict
32×33	33	✅ 无冲突

---

3.7 为什么只要 +1 就够？

因为：

• Bank 数量 = 32
• gcd(33, 32) = 1

👉 每行起点在 Bank 上 循环错位，永不重合

33 是 32 的"Bank 互质数"

---

3.8 工程经验口诀（背下来就不踩坑）

Shared Memory 矩阵 + 列访问
→ 行长度必须 ≠ Bank 数

最常见写法就是：

__shared__ float tile[32][32 + 1];

---

4. 现代解法：XOR Swizzling (异或置换)

到了 Ampere 和 Hopper 架构，Padding 开始显露弊端：

1. 浪费空间：Shared Memory 是寸土寸金的（H100 每个 SM 只有 228KB）。Padding 破坏了数据的紧凑性。
2. API 不兼容 ：现代的 Tensor Core 指令（如 ldmatrix）和异步拷贝指令（cp.async）往往要求数据在 Shared Memory 中是连续且对齐的。Padding 引入的空洞（Holes）会导致无法直接使用这些硬件加速指令。

从 Ampere (SM80) 开始，NVIDIA 在 Shared Memory 地址 → Bank 映射 中，引入了一个轻量级扰动函数，核心思想是：不要让 Bank 号只由低位线性决定

👉 float tile[32][32]，warp 内 按列访问 tile[tid][0]

4.1 Baseline：无 XOR（Volta / Turing）

地址（float index）

addr = tid * 32

Bank 规则

Bank = addr % 32

---

映射图（传统）

Thread:  0   1   2   3   4   ... 31
Addr:    0  32  64  96 128  ... 992
Bank:    0   0   0   0   0   ...  0

Bank 视角

Bank 0 : T0 T1 T2 T3 ... T31   ← 32-way conflict
Bank 1 :
Bank 2 :
...
Bank 31:

💥 确定性 32-way 冲突

---

4.2 Ampere / Hopper：XOR Swizzling 后

⚠️ 说明

NVIDIA 从未公开精确公式

下图是行为等价的抽象模型，用于理解"为什么有用 & 为什么有限"

---

1️⃣ Swizzling 的"直觉公式"

bank = (addr ⊕ (addr >> 5)) % 32

• >> 5：取"行号级别"的高位
• ⊕：把高位信息搅进 Bank index

---

2️⃣ 对我们的地址做 XOR

addr = tid << 5
addr >> 5 = tid

所以：

bank = (tid << 5 ⊕ tid) % 32

---

3️⃣ 结果映射（Ampere / Hopper）

Thread:  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 ...
Bank:    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 ...

Thread: 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
Bank:    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15

---

4️⃣ Bank 视角（Ampere / Hopper）

Bank 0 : T0  T16
Bank 1 : T1  T17
Bank 2 : T2  T18
...
Bank15 : T15 T31

Bank16-31 : 空

结果

• ❌ 不再是 32-way
• ⚠️ 但仍是 2-way conflict
• ⚠️ 且分布 不完全均匀

👉 Swizzling 起效了，但没"根治"

---

4.3 Blackwell：更激进的 Swizzling

Blackwell（SM100+）做了两件事：

1. XOR 源更多（不只一个高位）
2. 与访问模式 / 指令类型相关
3. Bank 选择逻辑更深

你可以把它理解为：

bank = f(addr_low_bits,
         addr_mid_bits,
         addr_high_bits,
         access_pattern,
         maybe_sm_internal_state)

---

1️⃣ Blackwell 的目标

不是你这个教科书式转置，而是：

• tensor-core 配套共享内存
• warp-group 访问
• irregular shared memory layouts
• AI kernel 的非规则 stride

---

2️⃣ 对"tid * 32"这种病态模式会发生什么？

关键事实（非常重要）：

Swizzling ≠ 创造信息
Swizzling 只能"重排已有 bit 熵"

而你的地址是：

tid * 32  →  低 5 位全 0

👉 输入本身就是"低熵"的

---

3️⃣ Blackwell 上的典型结果（抽象）

Thread:  0  1  2  3  4  5  6  7 ...
Bank:    0  2  4  6  8 10 12 14 ...

Thread: 16 17 18 19 20 21 22 23 ...
Bank:    1  3  5  7  9 11 13 15 ...

Bank 视角（示意）

Bank 0 : T0
Bank 1 : T16
Bank 2 : T1
Bank 3 : T17
...

听起来很美好？

⚠️ 注意：

• 这不是保证行为
• 不同 kernel / 指令 / SM 状态可能不同
• 你无法写代码去"依赖"它

---

4️⃣ 核心结论（Blackwell）

• ✅ 平均冲突更低
• ❌ 最坏情况仍可能出现
• ❌ 不可验证、不可设计、不可依赖

👉 工程上仍然当它"可能没有"

---

4.4 三代对比总结

列访问 tile[32][32]

Volta/Turing:
[ 32-way conflict ]  ← 全扎 Bank 0

Ampere/Hopper:
[ 2-way conflict ]   ← 被 XOR 打散

Blackwell:
[ maybe 1~2-way ]    ← 统计改善，但不确定

---

五、为什么 padding +1 是"永恒正确解"

一旦 padding：

addr = tid * 33

低位立刻变成：

addr % 32 = tid

映射（所有架构）

Thread:  0   1   2   3   ... 31
Bank:    0   1   2   3   ... 31

✔ 无冲突

✔ 可预测

✔ 可验证

✔ 架构无关

---

4.6 一句工程级结论

XOR Swizzling 是"统计优化"，Padding 是"结构性正确性"

• Swizzling：NVIDIA 帮你兜底
• Padding：你作为 kernel 设计者的责任

---

5. 实战：矩阵转置的演进

理论说得再多，不如代码跑一跑。本章的配套代码将通过一个经典的 Matrix Transpose 算子，演示三种实现方式的性能差异。

实验设计

我们将实现一个 Kernel，读取 32 × 32 32 \times 32 32×32 的数据块到 Shared Memory，转置后写回 Global Memory。

1. Naive Kernel：不做任何处理。读取时合并访问（快），写入时发生 32-way Conflict（极慢）。
2. Padded Kernel ：声明 smem[32][33]。冲突消除，性能提升，但浪费了 32 * 4 字节空间。
3. Swizzled Kernel：使用 XOR 逻辑重映射索引。冲突消除，空间零浪费。

[💻 代码占位符：参见项目 examples/02_memory_optim/12_shared_mem_bank_conflict.cu]

• 代码将包含：使用 Nsight Compute 的 l1tex__data_pipe_lsu_wavefronts_mem_shared 指标来量化 Bank Conflict 的发生次数。

---

6. 总结与下章预告

• Bank Conflict 是 Shared Memory 性能的头号杀手，它会引发指令重播（Replay）。
• 对于传统 CUDA 程序，Padding 是最简单的解药。
• 对于面向 Tensor Core 的现代程序（Hopper/Blackwell），XOR Swizzling 是必须掌握的技能，它是连接 cp.async 和 ldmatrix 的桥梁。

至此，我们已经解决了 Global Memory (Ch 11) 和 Shared Memory (Ch 12) 的带宽问题。但还有一个存储区域，它比 Shared Memory 更快，也更容易成为瓶颈------那就是寄存器。

👉 下一章：[Module B] 13. 寄存器管理：Register Spilling 与 Occupancy 的博弈

为什么寄存器用多了反而会变慢？如何通过 __launch_bounds__ 和编译器指令精准控制寄存器用量？下一章我们将深入 SM 的心脏。

---

📚 参考文献与延伸阅读

1. NVIDIA CUDA C++ Programming Guide - Shared Memory
   • 官方文档第 5.3.2.5 节。这是关于 Bank 结构最权威的说明，包含了不同架构（如 Volta vs Ampere）Bank Width 的变化。
   • Link
2. CUTLASS: Efficient Matrix Multiply on GPUs
   • CUTLASS 源码中的 GemmSharedLoadIterator 是 XOR Swizzling 的工业级教科书实现。
   • GitHub Link
3. Parallel Forall: Efficient Matrix Transpose
   • 一篇经典的官方技术博客，虽然年代久远，但对 Bank Conflict 的图解依然是最好的入门材料。
4. https://www.cs.nthu.edu.tw/\~cherung/teaching/2010gpucell/CUDA04.pdf