滑动窗口算法是处理子数组 / 子字符串最值问题的高效利器,核心思想是通过维护一个动态调整的 "窗口"(由左右指针界定),在一次遍历中完成对数据的筛选和统计,将暴力解法的 O(n2) 时间复杂度优化到 O(n),是算法面试中高频且易掌握的核心技巧。
本文将结合3道经典题目 ------"最大连续 1 的个数 III" , "无重复字符的最长子串","长度最小的子数组"基于实战代码拆解滑动窗口的解题思路,带你理解 "窗口为何动、何时动、怎么动" 的核心逻辑。
滑动窗口算法的核心原理
滑动窗口本质是双指针(左指针 left + 右指针 right) 的应用,窗口的 "滑动" 体现在两个维度:
- 扩展:右指针向右移动,将新元素纳入窗口,探索更大的解空间;
- 收缩:当窗口内元素不满足题目约束时,左指针向右移动,剔除窗口左侧元素,直到约束重新满足;
- 更新结果:在窗口调整的过程中,持续统计符合条件的窗口最值(长度 / 和等)。
滑动窗口的关键优势在于:避免了暴力解法中 "重复检查子数组 / 子字符串" 的冗余操作。
例题1
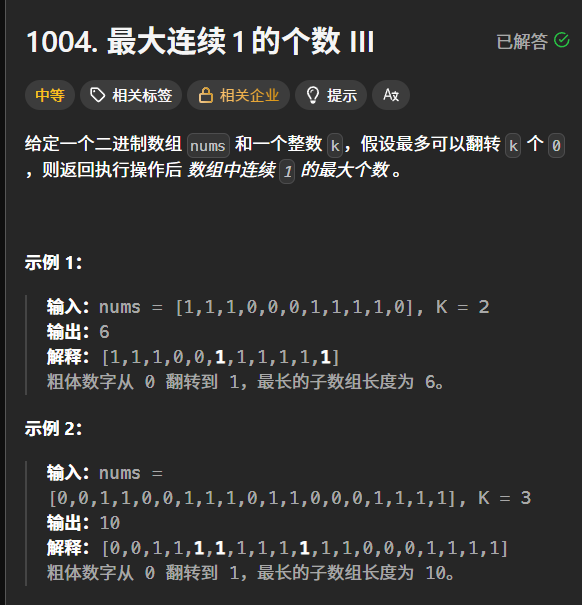
1004. 最大连续1的个数 III - 力扣(LeetCode)
思路分析
这道题可以转化为:寻找一段最长的子区间,使得区间内 0 的个数不超过 k 个。按照这样的思路我们就可以借用"滑动窗口"的思想来解决这道题。
核心约束与窗口定义
- 窗口约束:窗口内 0 的数量 ≤ k(最多翻转 k 个 0);
- 左指针
left:窗口左边界,负责收缩窗口; - 右指针
right:窗口右边界,负责扩展窗口; - 计数器
count:统计当前窗口内 0 的数量; - 结果
result:记录满足约束的最大窗口长度(即最大连续 1 的个数)。
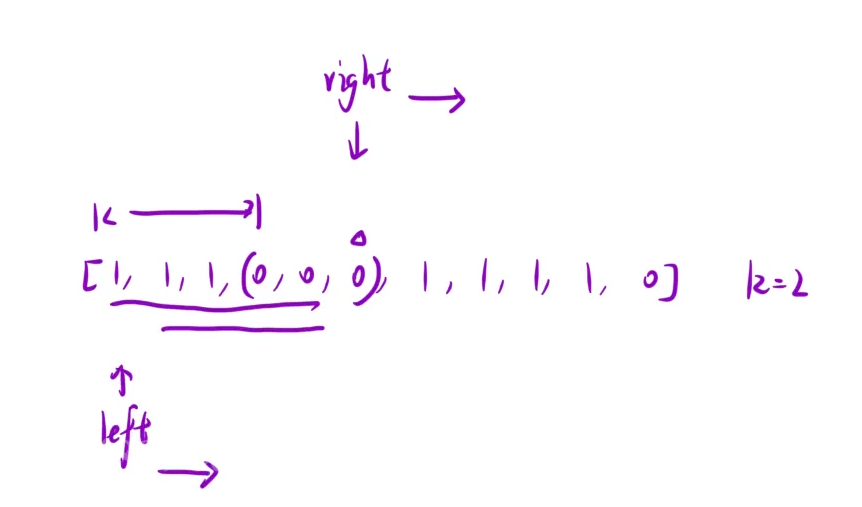
我们以数组[1,1,1,0,0,0,1,1,1,1,0]为例,并约定k=2。
初始时,left和right指针都指向数组的第一个元素。随后,right指针开始向右扩展窗口。
当right移动到图中所示位置时,窗口内 0 的个数超过了 k=2,此时需要对窗口进行调整。
如果我们只将 left指针右移一位(指向数组的第二个元素),并让right指针重新从左侧开始搜索,这样的时间复杂度仍然很高。
不难发现,当left指针在索引 0-3 的位置时,right指针最多只能移动到索引 5 的位置。也就是说,以索引 5 为右端点的最大有效滑动窗口,其左端点的初始位置就是left 在索引 0 的地方。
因此,我们可以采用更高效的处理方式:
当窗口内 0 的个数超过k时,保持 right指针不动,只移动 left指针收缩窗口,直到窗口内 0 的个数小于等于k,再继续移动right指针扩展窗口。
代码示例
java
public static int longestOnes(int[] nums, int k) {
int result=0; // 最终结果:最大连续1的个数
int n=nums.length;
int left=0; // 窗口左指针
int count=0; // 窗口内0的数量
// 右指针遍历数组,扩展窗口
for (int right = 0; right < n; right++) {
// 新元素是0,更新窗口内0的计数
if(nums[right]==0) {
count++;
}
// 关键:窗口内0的数量超过k,收缩左指针直到约束满足
while(count>k) {
if(nums[left]==0) {
count--;
}
left++;
}
// 每次扩展/收缩后,更新最大窗口长度
result=Math.max(result, right-left+1);
}
return result;
}关键逻辑解释
- 扩展窗口:右指针逐个遍历元素,遇到 0 就增加计数,这一步是 "探索可能的更长窗口";
- 收缩窗口 :当 0 的数量超过 k 时,必须移动左指针缩小窗口 ------ 这里的核心是先判断左指针当前元素是否为 0,再移动左指针,否则会漏掉对移出元素的计数更新,导致窗口约束失效;
- 更新结果:每一次窗口调整后,计算当前窗口长度,保留最大值,因为 "满足约束的窗口长度" 就是当前能得到的连续 1 的个数。
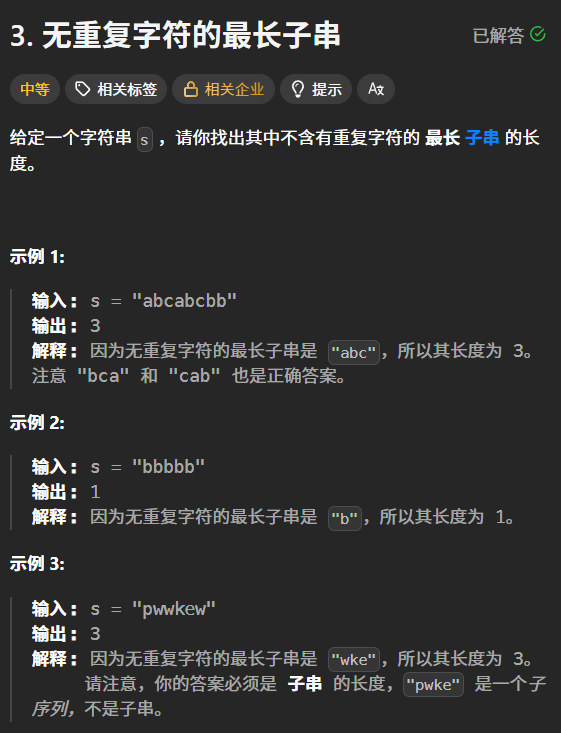
例题2
思路分析
我们可以借助哈希表来高效解决这个问题,哈希表中存储的是每个字符,以及该字符最后一次出现的索引位置。
右指针right向右遍历时,若当前字符已存在于哈希表中,且该字符的上次出现位置在当前窗口内(即 ≥ 左指针left),我们就直接将左指针left跳转到该字符上次出现位置的下一位,以此收缩窗口。
需要注意的是:无论当前字符是否已存在于哈希表中,每遍历到一个字符,都需要更新它在哈希表中的最新索引,以保证后续判断的准确性。
核心约束与窗口定义
-
窗口约束:窗口内无重复字符;
-
左指针
left:窗口左边界,当出现重复字符时,直接跳转到重复字符的下一位; -
右指针
right:窗口右边界,逐个遍历字符扩展窗口; -
哈希表
map:记录字符最新出现的索引(用于快速判断重复 + 更新左指针); -
结果
result:记录无重复字符的最大窗口长度。
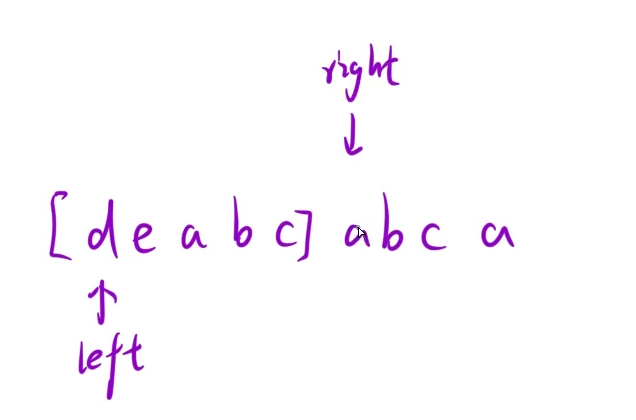
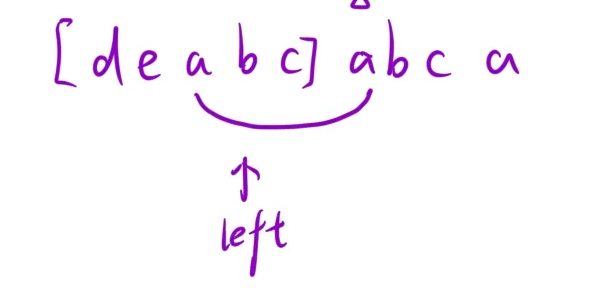
我们以字符串 "deabcabca" 为例,初始时 left 和 right 都指向字符 d,随后 right 向右移动扩展窗口。
当 right 移动到图中所示的位置(再次遇到字符 a)时,由于当前窗口 [d, e, a, b, c] 中已经包含了字符 a,此时就需要对窗口进行调整。
如果按照朴素的逻辑,我们会让 left 逐个向右移动,从下一个字符开始重新检查。但不难发现,以第二个位置为起点的子串,其长度肯定不会比之前的更长(因为少了第一个字符),这样做效率很低。
于是我们可以直接让 left 指针跳转到当前重复字符 a 的下一位,这样就大大提升了效率。
接下来 right 指针也不需要再回来重新探索,因为 [left, right] 这个区间内的元素肯定是不重复的,right只需要接着向右扩大窗口即可。
代码示例
java
public static int lengthOfLongestSubstring(String s) {
Map<Character, Integer> map=new HashMap<>(); // 字符 -> 最新索引
int left=0; // 窗口左指针
int result=0; // 最长无重复子串长度
for (int right = 0; right < s.length(); right++) {
Character c=s.charAt(right); // 当前右指针指向的字符
// 关键:字符已存在,且该字符在当前窗口内(索引≥left)
if(map.containsKey(c) && map.get(c)>=left) {
// 左指针跳转到重复字符的下一位,收缩窗口
left=map.get(c)+1;
}
// 更新字符的最新索引(无论是否重复都要更新)
map.put(c, right);
// 计算当前窗口长度,更新最大值
result=Math.max(result, right-left+1);
}
return result;
}关键逻辑解释
- 重复判断 :哈希表存储字符的最新索引,当遍历到字符
c时,若c已存在且其索引≥左指针,说明c在当前窗口内重复,必须调整左指针; - 窗口收缩 :左指针直接跳转到
map.get(c)+1(而非逐次右移),这是很重要的优化 ------ 因为[left, map.get(c)]区间内的子串必然包含重复字符,无需逐一遍历; - 索引更新:无论字符是否重复,都要更新其在哈希表中的索引,确保后续判断的是 "最新位置"。
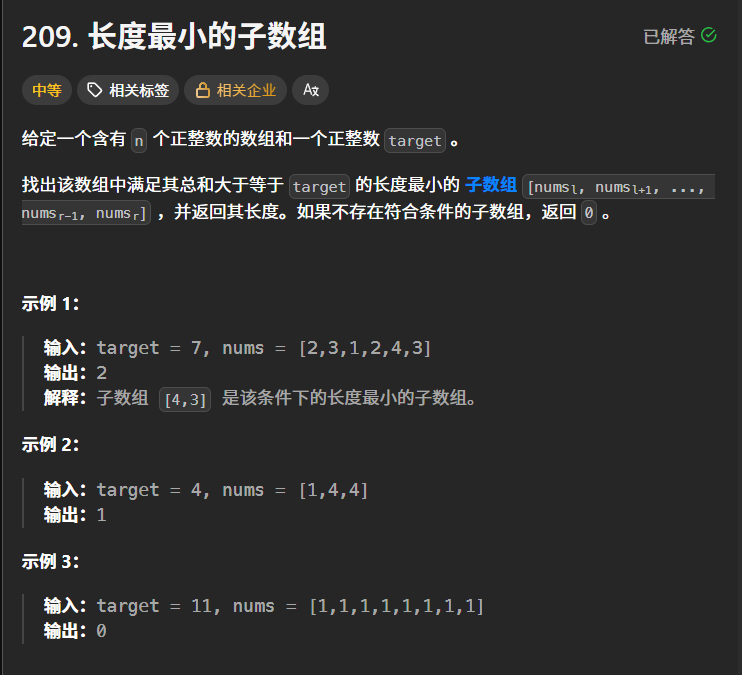
例题3
思路分析
本题我们可以定义一个j指针来表示窗口的终止位置,i指针表示窗口的起始位置,j从开始位置一直向右移动,同时用一个变量sum来累加j位置的和。
当sum的结果大于等于target之后,这个时候就需要移动i指针来缩小窗口的大小了。
核心约束与窗口定义
- 窗口约束:窗口内元素的和 ≥ target;
- 左指针
i:窗口左边界,负责收缩窗口; - 右指针
j:窗口右边界,负责扩展窗口; - 变量
sum:统计当前窗口内元素的和; - 结果
result:记录满足约束的最小窗口长度。
代码示例
java
public int minSubArrayLen(int target, int[] nums) {
int result = Integer.MAX_VALUE; // 初始化为最大值,用于后续取最小
int i = 0; // 窗口左指针(起始位置)
int sum = 0; // 窗口内元素的和
for (int j = 0; j < nums.length; j++) {
sum += nums[j]; // 右指针扩展窗口,累加元素和
// 当窗口和满足条件时,尝试收缩左指针,寻找更小窗口
while (sum >= target) {
int temp = j - i + 1; // 计算当前窗口长度
// 移动左指针,收缩窗口
sum -= nums[i];
i++;
// 更新最小长度
result = Math.min(temp, result);
}
}
// 如果result仍为最大值,说明无满足条件的子数组,返回0
return result == Integer.MAX_VALUE ? 0 : result;
}关键逻辑解释
- 扩展窗口 :右指针
j逐个遍历数组,将元素加入窗口并累加和,探索可能的满足条件的窗口; - 收缩窗口 :当窗口和
sum大于等于target时,移动左指针i收缩窗口,同时更新最小长度 ------ 这一步是 "在满足条件的前提下,尽可能缩小窗口"; - 结果处理 :若遍历结束后
result仍为初始的最大值,说明没有任何子数组满足条件,返回 0;否则返回最小长度。
结语
滑动窗口算法的核心是"动态维护符合约束的窗口",解决子数组 / 子字符串最值问题时,只要能明确 "窗口的约束条件","扩展规则","收缩规则",就能将复杂问题简化。
对于本文的三道题:
- 处理 "最大连续 1 的个数 III" 时,重点是统计窗口内不符合条件的元素(0),并逐次收缩窗口;
- 处理 "无重复字符的最长子串" 时,重点是通过哈希表快速定位重复元素,优化窗口收缩效率;
- 处理 "长度最小的子数组" 时,重点是在满足和的条件下,尽可能收缩窗口以找到最小长度。