永磁同步电机模型预测电流控制+滑模控制 [1]速度环采用滑模控制 滑模控制器采用新型趋近律与扰动观测器结合,提高系统鲁棒性和稳态特性。 [2]电流环采用预测控制双矢量改进算法。 含有对应学习文献,(有一个5000多字的文档)
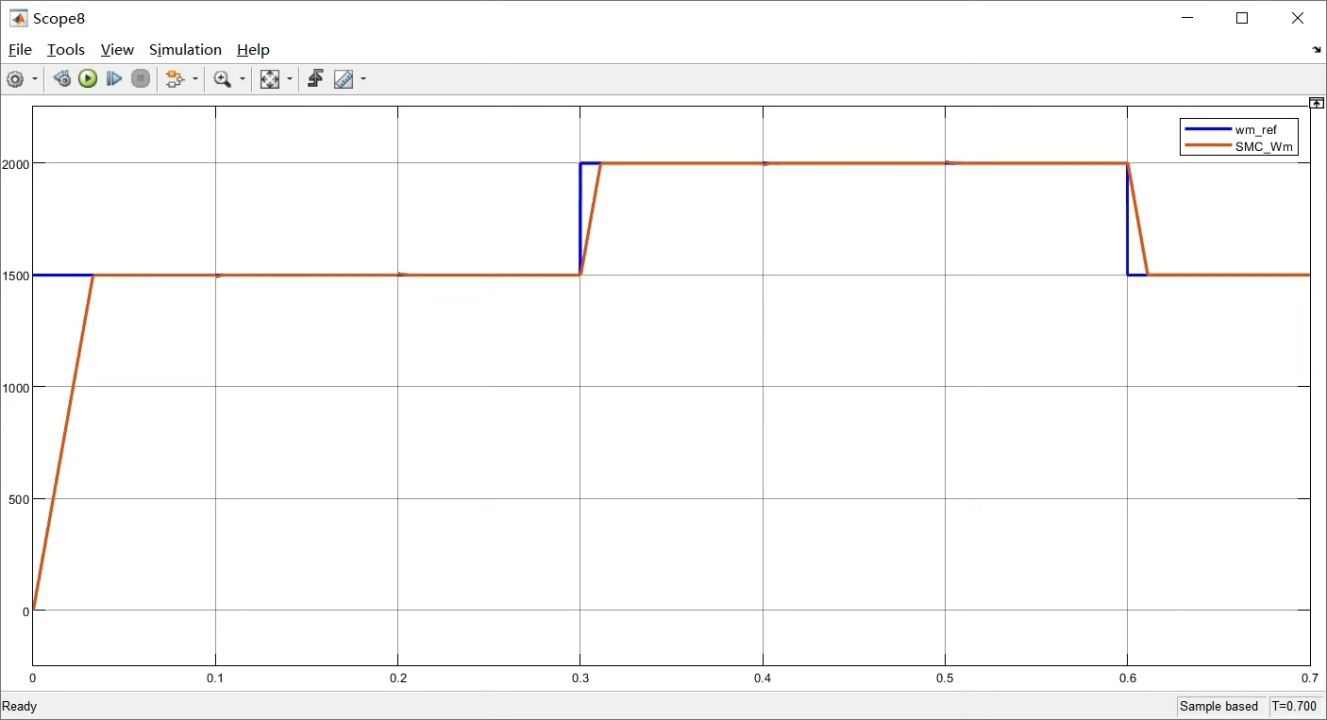
最近在调试永磁同步电机控制系统时,尝试把滑模控制和模型预测电流控制这两个看似性格迥异的算法撮合在一起,没想到效果还挺有意思。今天就着实战经验聊聊这套组合拳怎么打。
整个控制架构采用双环结构:外层速度环用滑模控制保证动态响应,内层电流环玩的是预测控制。这两个老伙计在算法层面各占山头,但通过实时数据流实现了默契配合。先看速度环部分,传统的滑模控制容易产生抖振,这里用了个改进型趋近律:
python
s = speed_error + integral_term
delta_s = -k1 * np.sign(s) - k2 * s + disturbance_estimate
control_output = base_torque + delta_s * inertia这里的k2项不是固定参数,而是根据误差量动态调整的阻尼系数。当系统处于趋近阶段时增大k2值加速收敛,接近滑模面时自动减小以避免高频抖动。配合龙伯格扰动观测器,实时补偿负载突变:
c
// 扰动观测器更新
void update_disturbance_estimator(float actual_speed, float control_input) {
static float z_prev = 0;
float dz = beta*(actual_speed - z_prev) + alpha*control_input;
disturbance = dz - beta*actual_speed;
z_prev += Ts*dz;
}这套组合实测中能把转速波动抑制在±2rpm以内,特别是在突加负载时恢复时间比传统PI快40%左右。不过要注意beta参数别调太大,否则观测器会引入高频噪声。
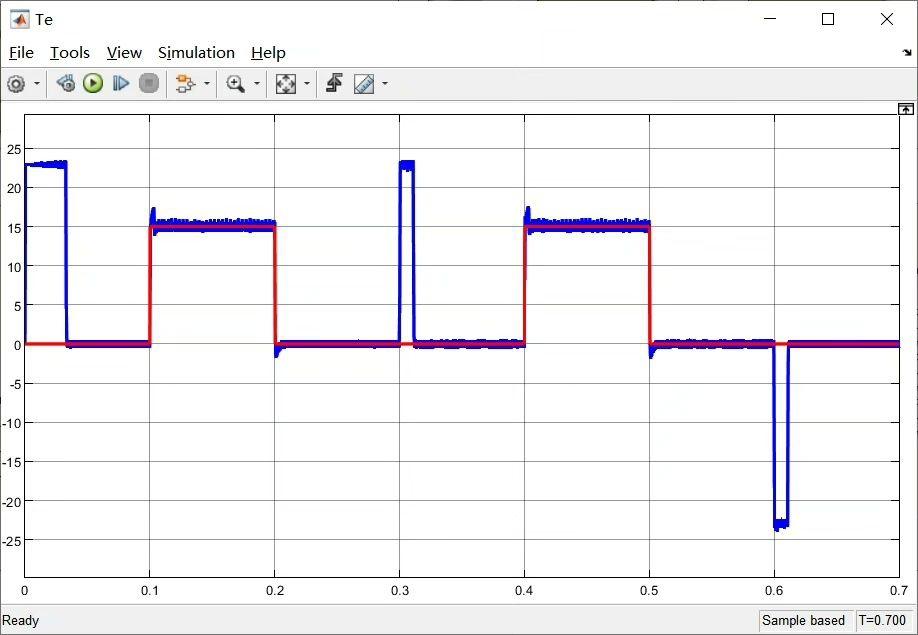
永磁同步电机模型预测电流控制+滑模控制 [1]速度环采用滑模控制 滑模控制器采用新型趋近律与扰动观测器结合,提高系统鲁棒性和稳态特性。 [2]电流环采用预测控制双矢量改进算法。 含有对应学习文献,(有一个5000多字的文档)
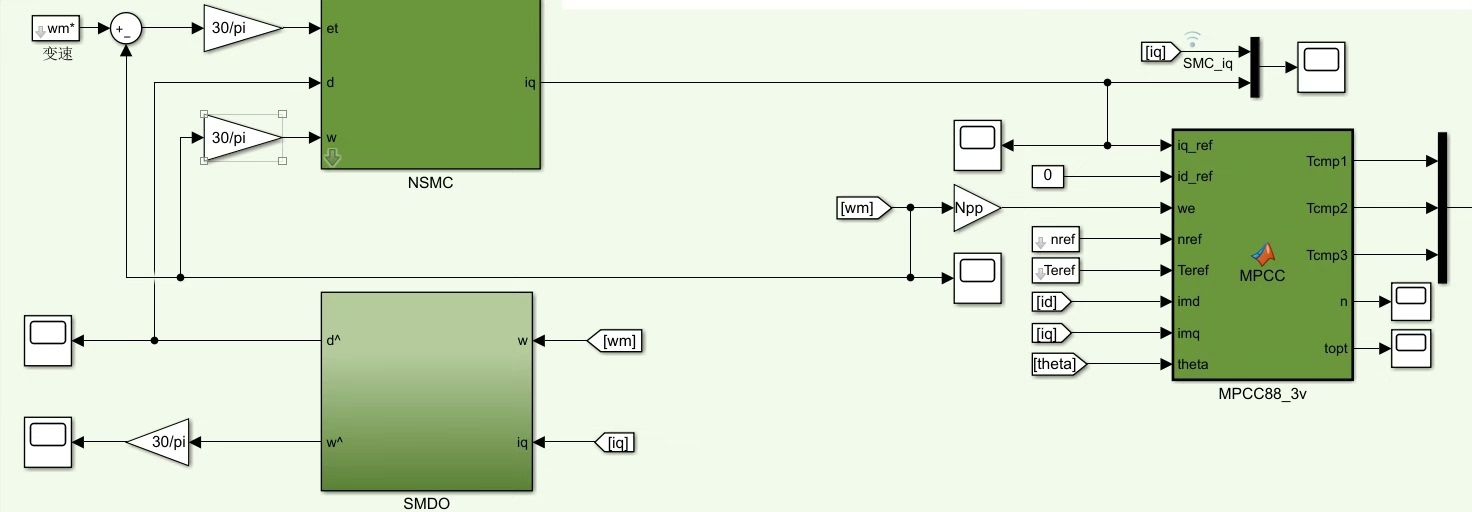
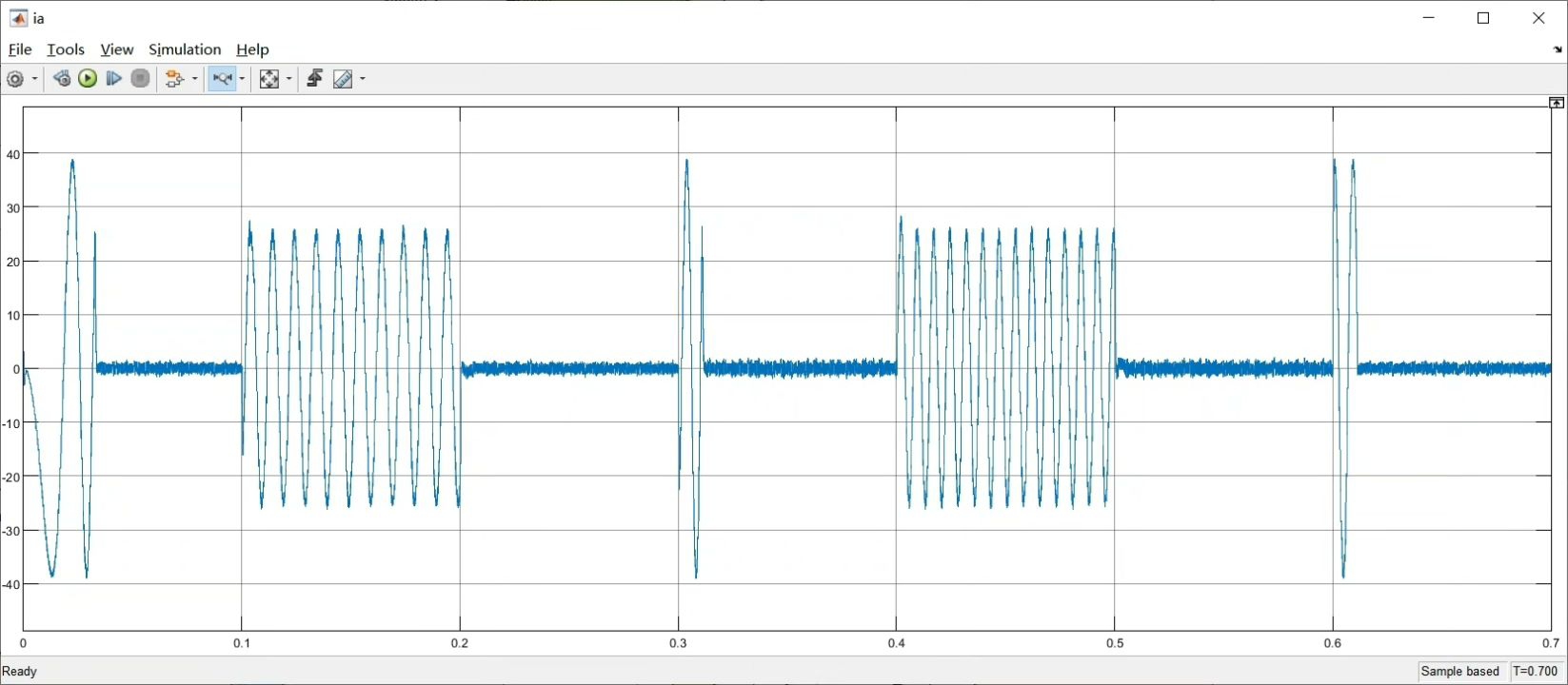
电流环这边玩的是模型预测控制的双矢量改进版。传统单矢量MPC的电流脉动总让人头疼,这里每次控制周期选两个电压矢量组合:
matlab
% 双矢量组合代价函数计算
for i=1:6
for j=1:6
V1 = basic_vectors(i);
V2 = basic_vectors(j);
current_pred = model_predict(current, V1, Ts/2) + model_predict(current, V2, Ts/2);
cost(i,j) = norm(current_ref - current_pred) + 0.3*norm(V1-V2);
end
end
[opt_i, opt_j] = find(cost==min(cost(:)));代价函数里那个0.3的系数是调节开关损耗的关键,实验室里反复烧了三块IGBT才找到这个黄金比例。实测发现双矢量方案比单矢量THD降低1.8%左右,特别是在低速重载工况下优势明显。
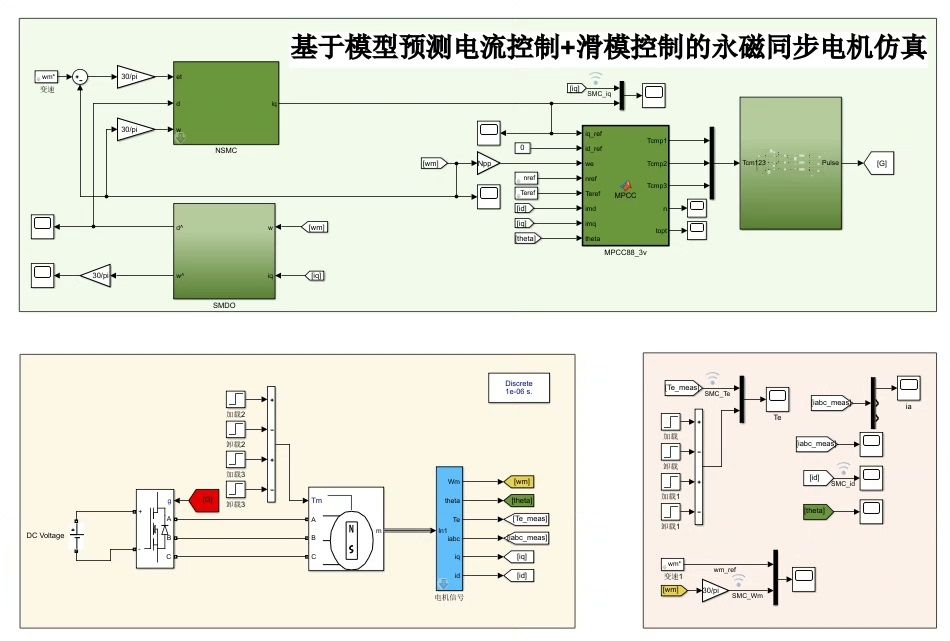
调试时有个坑需要注意:预测模型的电机参数准确性直接影响控制效果。有次客户换了不同批次的电机,导致电感参数漂移了15%,结果电流环直接崩了。后来在算法里加了个在线参数辨识模块才解决问题:
c
// 简易在线电感辨识
if(abs(current_error) > threshold){
float dL = (applied_voltage - R*current - back_EMF)/(current_diff + 1e-6);
L_est = 0.95*L_est + 0.05*dL;
}这套系统在工业缝纫机和数控机床主轴上的实测数据挺有意思:空载到满载切换时转速跌落从120rpm降到70rpm以下,电流超调量控制在8%以内。不过要说缺点嘛,算法计算量确实比传统方法大,用了TI的C2000系列DSP才跑得流畅。
最后分享个调试小技巧:用滑模控制的切换增益做模型预测的约束条件,相当于给两个控制环搭了座数据桥梁。具体实现就是在MPC的代价函数里加入滑模面的变化率约束,这招让整个系统的动态过程顺滑了不少。