Day44 动态规划part04

背包问题

1. 01背包问题：每件物品只能用一次
2. 完全背包问题：每件物品可以使用无数次

01背包问题

1. 暴力解法：每一件物品其实只有两个状态，取或者不取，所以可以使用回溯法搜索出所有的情况，那么时间复杂度就是 o ( 2 n ) o(2^n) o(2n)，这里的n表示物品数量。
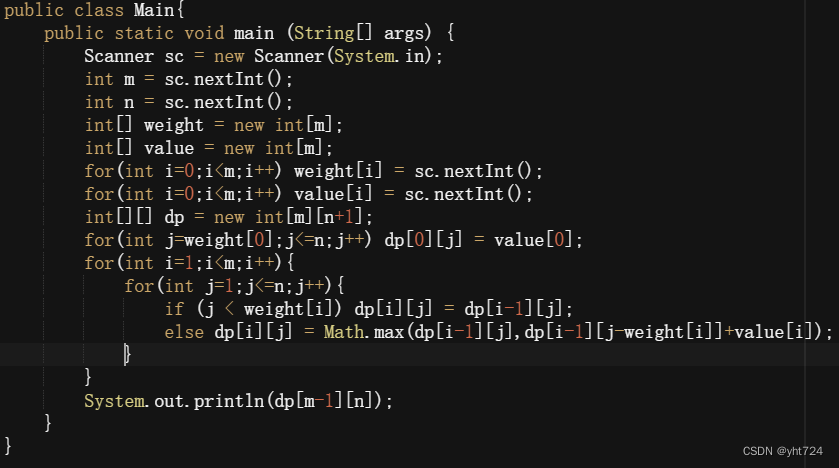
2. 动态规划：dpij 表示从下标为0-i的物品里任意取，放进容量为j的背包，价值总和最大是多少。
3. 对于物品i：
   • 不放物品i：由dpi - 1j可知，即从下标为0到i-1的物品里任意取，放进容量为j的背包，价值总和最大是多少。也可以理解为背包容量为j，里面不放物品i的最大价值，此时dpij==dpi - 1j。
   • 放物品i：由dpi - 1j - weight\[i]可知，dpi - 1j - weight\[i] 为背包容量为j - weighti的时候不放物品i的最大价值，那么dpi - 1j - weight\[i] + valuei （物品i的价值），就是背包放物品i得到的最大价值
   • 得到递推公式： dpij = max(dpi - 1j, dpi - 1j - weight\[i] + valuei);
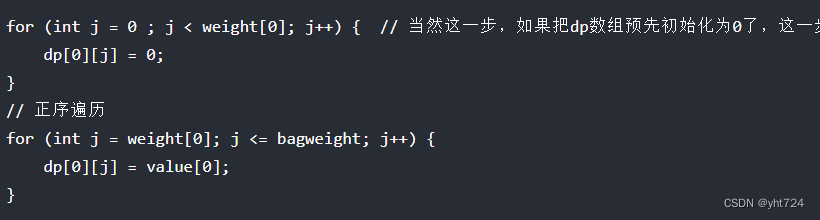
4. 初始化：
   • 当j为0的时候，不管不放物品，背包中的价值都是0
   • 当i为0的时候，即每次选择0物品放入各个大小的背包中，当且仅当j>=weighti才会有valuei的价值
     
     

01背包-滚动数组

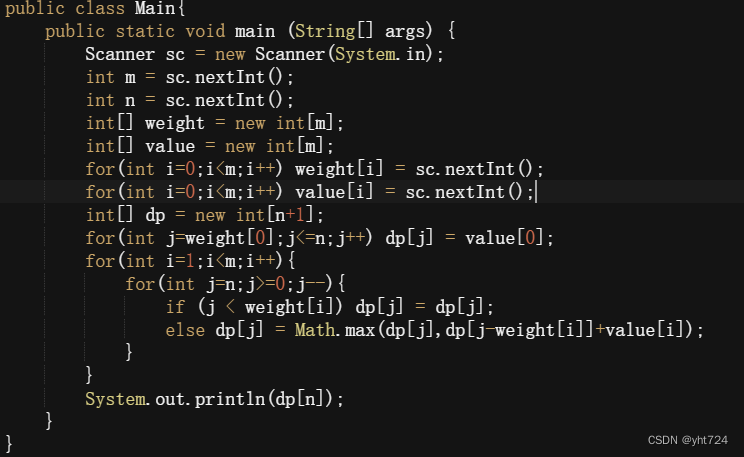
1. 对于二维dp数组：dpij = max(dpi - 1j, dpi - 1j - weight\[i] + valuei);如果在i维度进行叠加，即将i-1上的所有值拷贝到i上，递归公式变成：dpij = max(dpij, dpij - weight\[i] + valuei);
2. 因此将二位dp数组变成一维数组，得到递归公式dpj = max(dpj,dpj-weight\[i]+valuei)
   • 一维dp数组的含义：重量为j的背包中装的价值最大的物品是dpj
3. 二维dp数组的遍历顺序是从上到下从左到右
4. 一维dp数组的遍历顺序
   • i：0-》weight.length-1
   • j：bagweight-》0
   • j不是0-》bagweight是因为如果是正序遍历，背包重量j中的价值dpj可能等于dpj-weight\[i]+valuei，而dpj-weight\[i]可能就已经蕴含了valuei将重复计算
   • j倒序遍历是为了保证物品i只被放入一次，i的正序遍历是为了保证所有的物品都被判断过
     

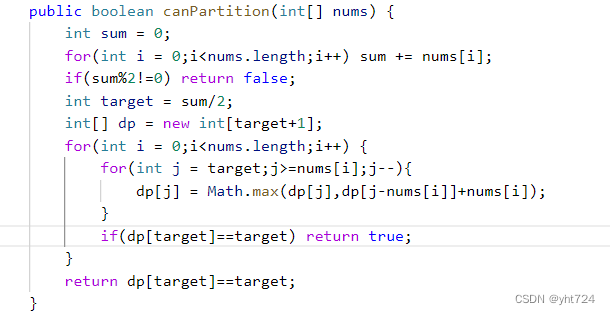
LC416分割等和子集(未掌握)

1. 只给定了一个数组，因此这个数组即是weight又是value
2. if(j<weighti) dpj = dpj;else dpj = Math.max(dpj,dpj-weight\[i]+valuei)可以转换为for(int j = n;j>=weighti;j--)
3. 剪枝操作：在第二层循环中加入if(dptarget==target) return true;
4. 代码