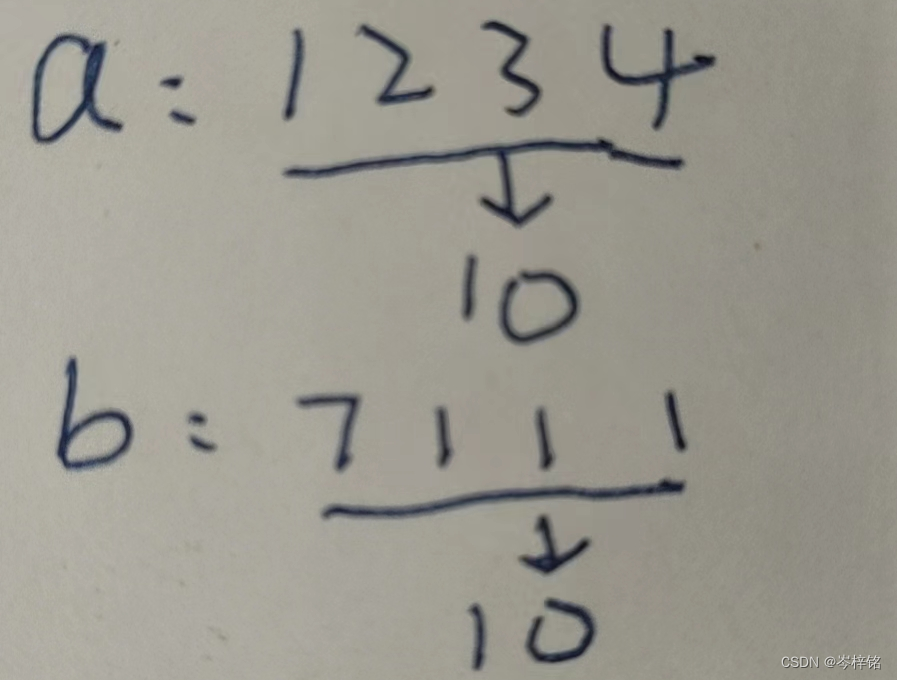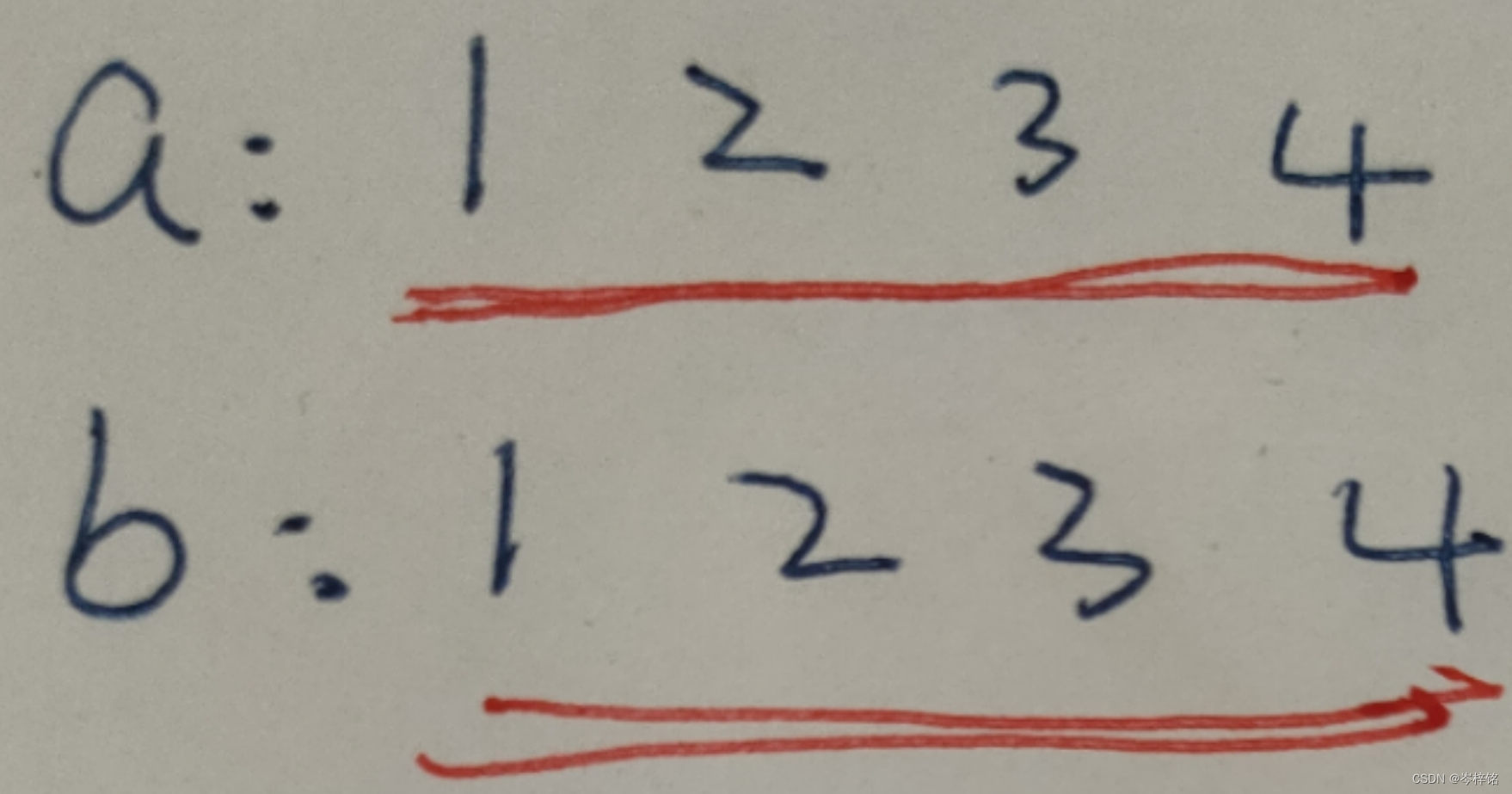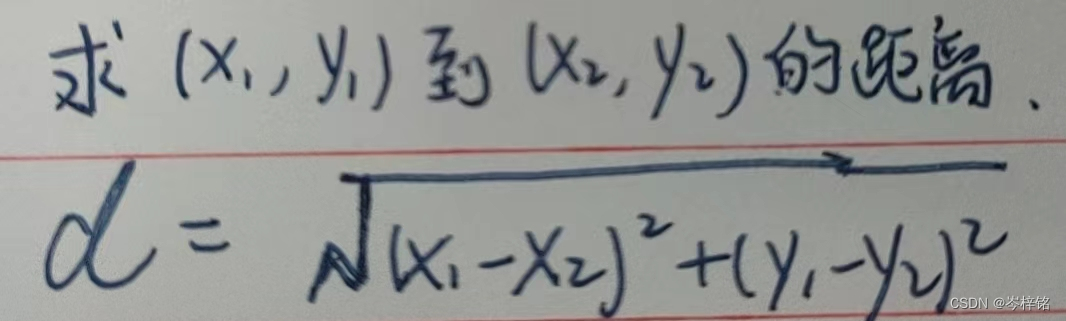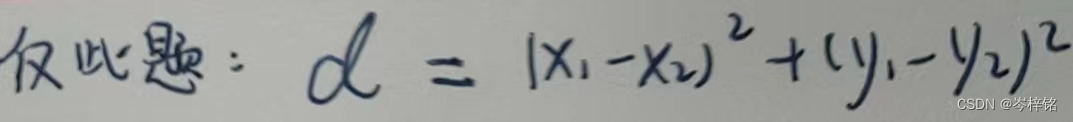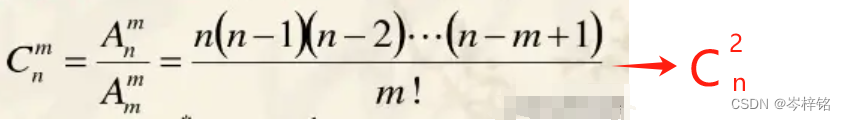今天5月30号,特么的昨天下午还体测,体测完塔玛的帮别人跑1000米还塔玛的被抓了,吃个处分他娘的直接没心情学了,29号塔玛得一天没学死臭咯,现在看看能写出几道题吧,还有2天时间
一、蓝桥杯不知第几届编程题:合并数列(中难)

【思路】:双指针、前缀和
(当然大家都知道java里没有指针,我这里就是用2个index代替指针的作用来找对应下标的数而已)
首先我们根据题意可以确定几点:
1、这两个数组的 "和" 一定一样!
2、所有数都是正整数
3、根据前面的点我们可以确定,不管哪个数组,从左往右加都必然是【单调递增】的
4、那么最糟糕的情况 就是两个数组只能合并成一个数字,这样时两个数组的总和才一样
5、如果两个数组是一模一样 ,就不用分割合并数组
6、最后注意一下!注意一下! 【合并次数】
两个数组任意一个合并一次都要算入合并次数里
然后注意!两种情况分别对应两种【合并次数】
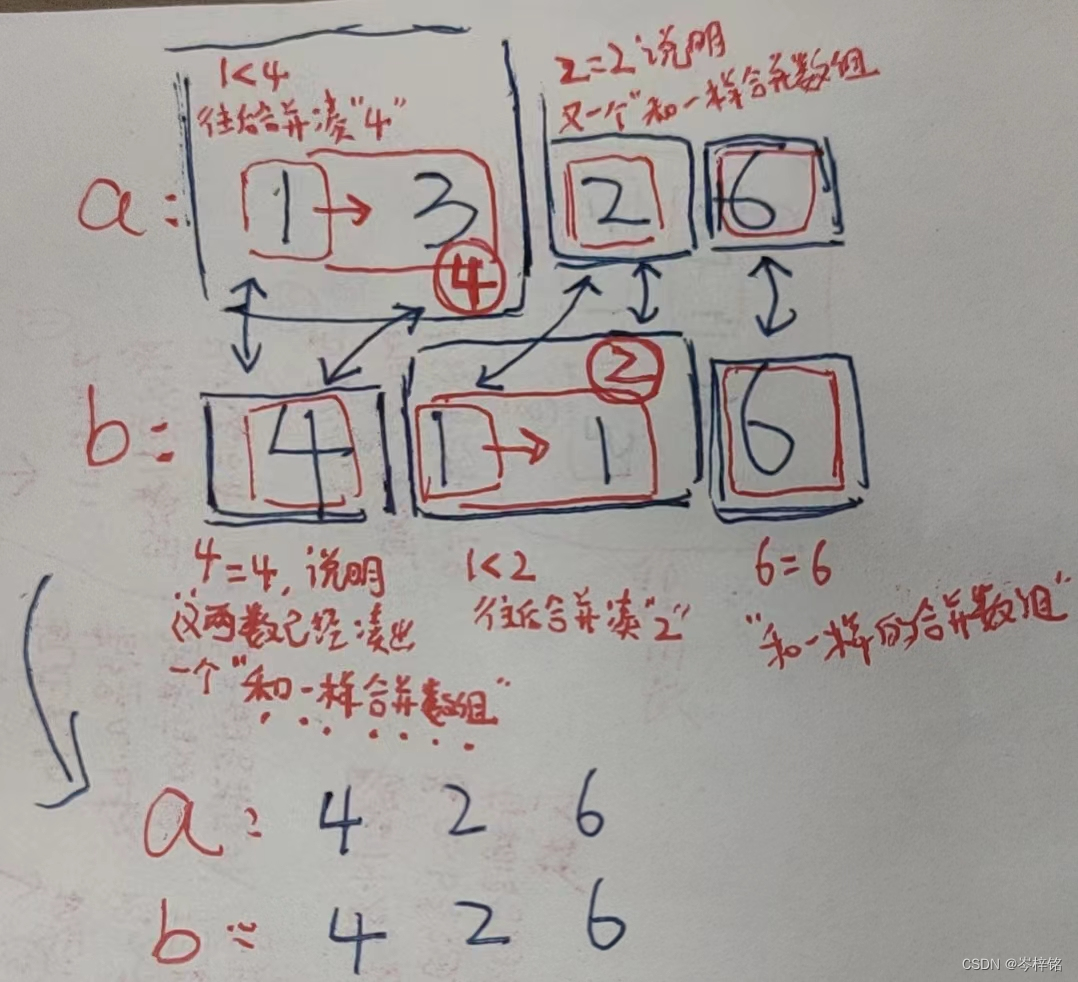
(1)普通情况:当可以凑成和一样 的时候,优先合并成和一样的;
(2)最糟糕情况:而没有和一样的数组 的时候,就只能不断两个两个的合并,直到出现两个相同和的两个数组!!!有点抽象,看图片例子!!
当是最糟糕情况时:只能不断两个两个的合并
一般情况时:优先合并成和一样的
那么既然涉及到数组和,我第一个想到的就是前缀和(就是记录递增和的数组)
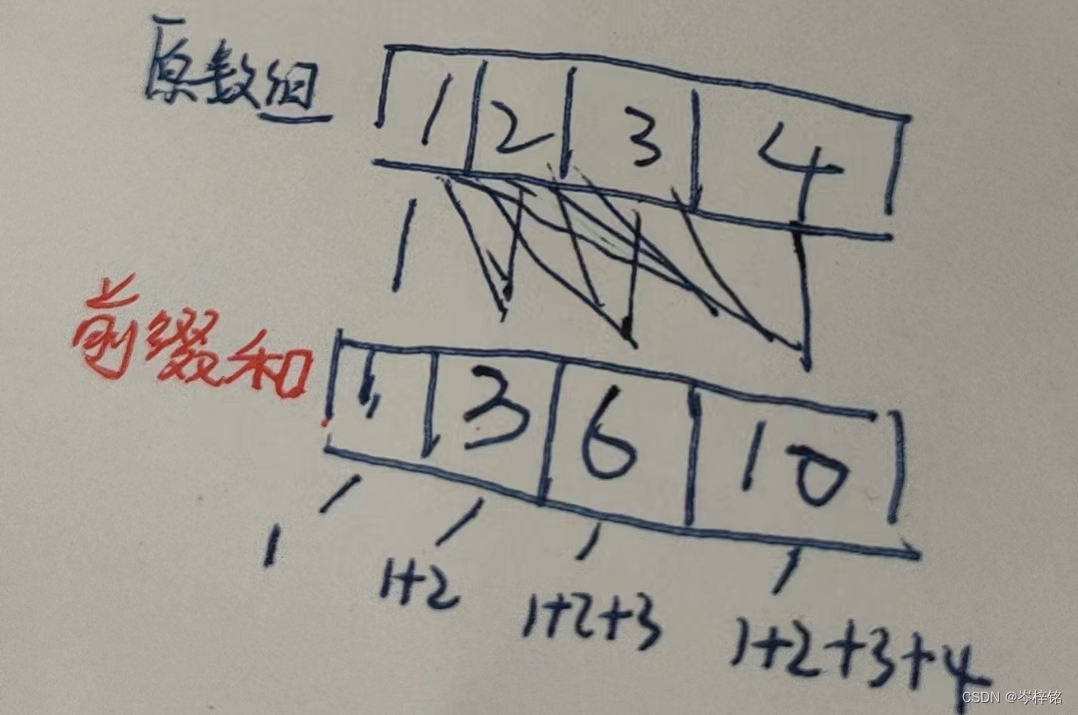
那么当我把多组数据的前缀和对比,发现一个规律:
无论什么情况,如果遍历这两个数组时,
【数组a的前缀和不等于数组b前缀和的时候 】百分之一万要合并数组!!!!
【当数组a前缀和等于数组b前缀和的时候 】,就说明已经在相同和的合并数组里了,啥也不用管只管往后遍历就行。
看下面图理解:
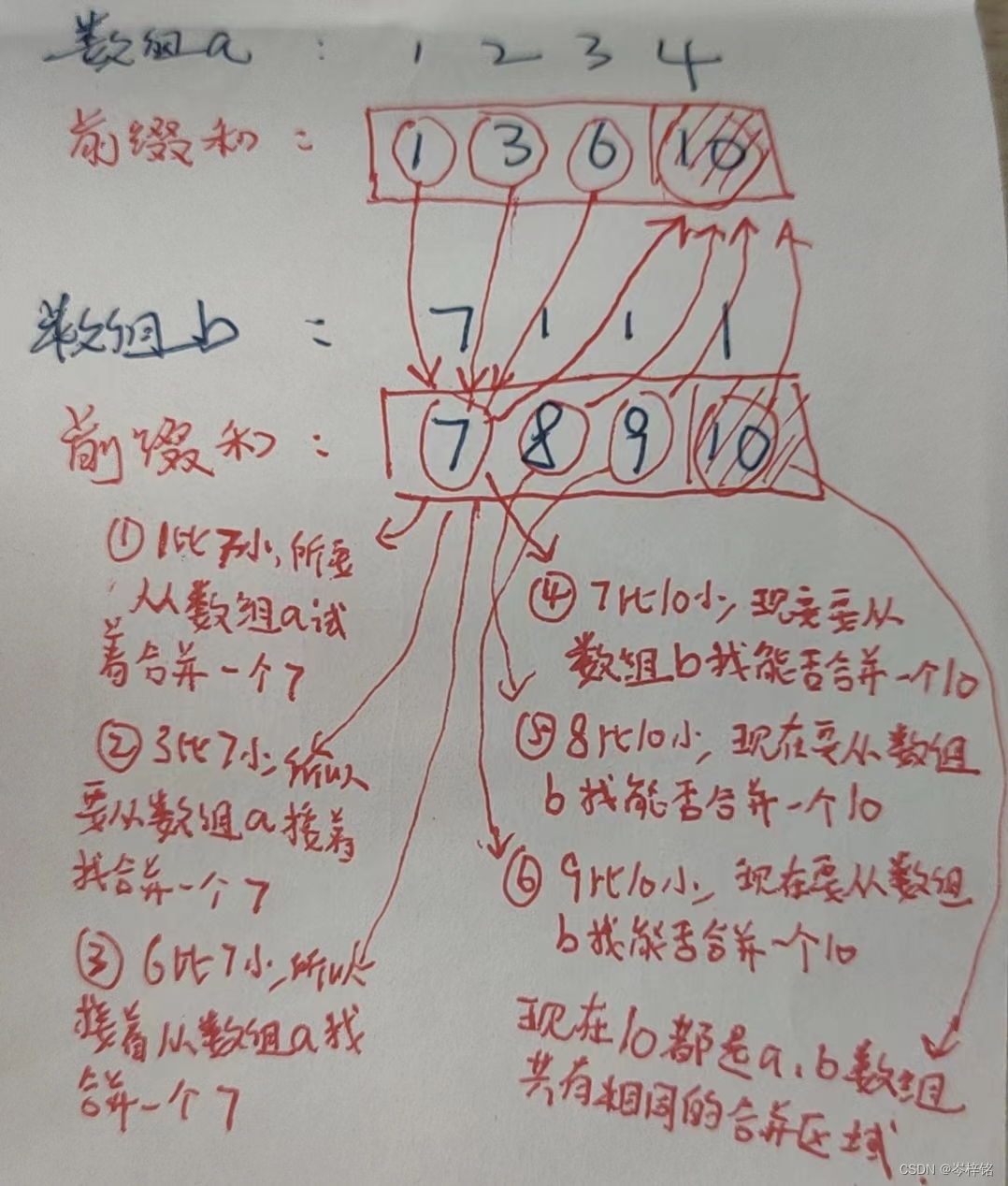
【数组a的前缀和不等于数组b前缀和的时候,百分之一万要合并数组】
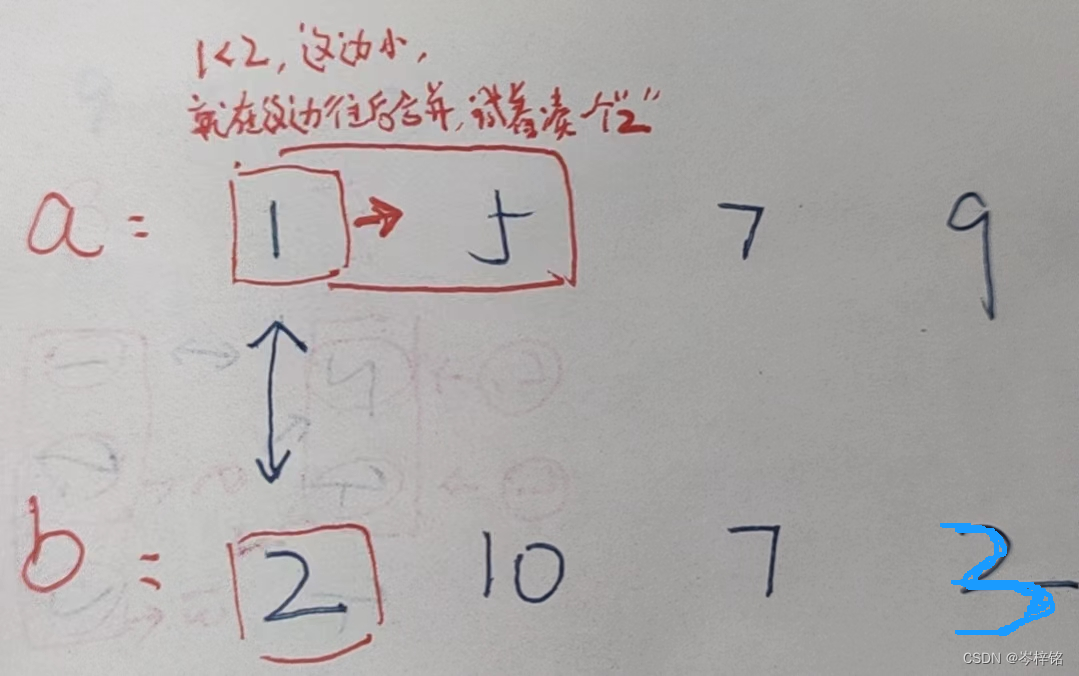
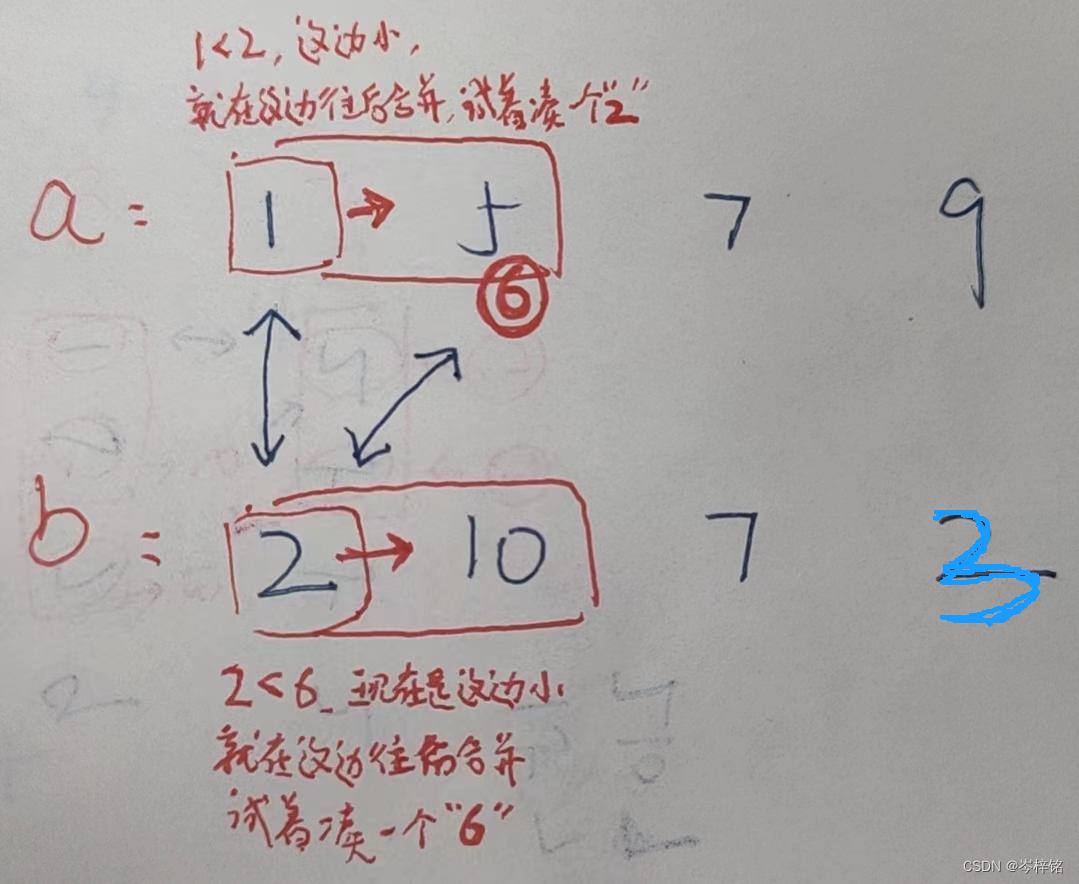
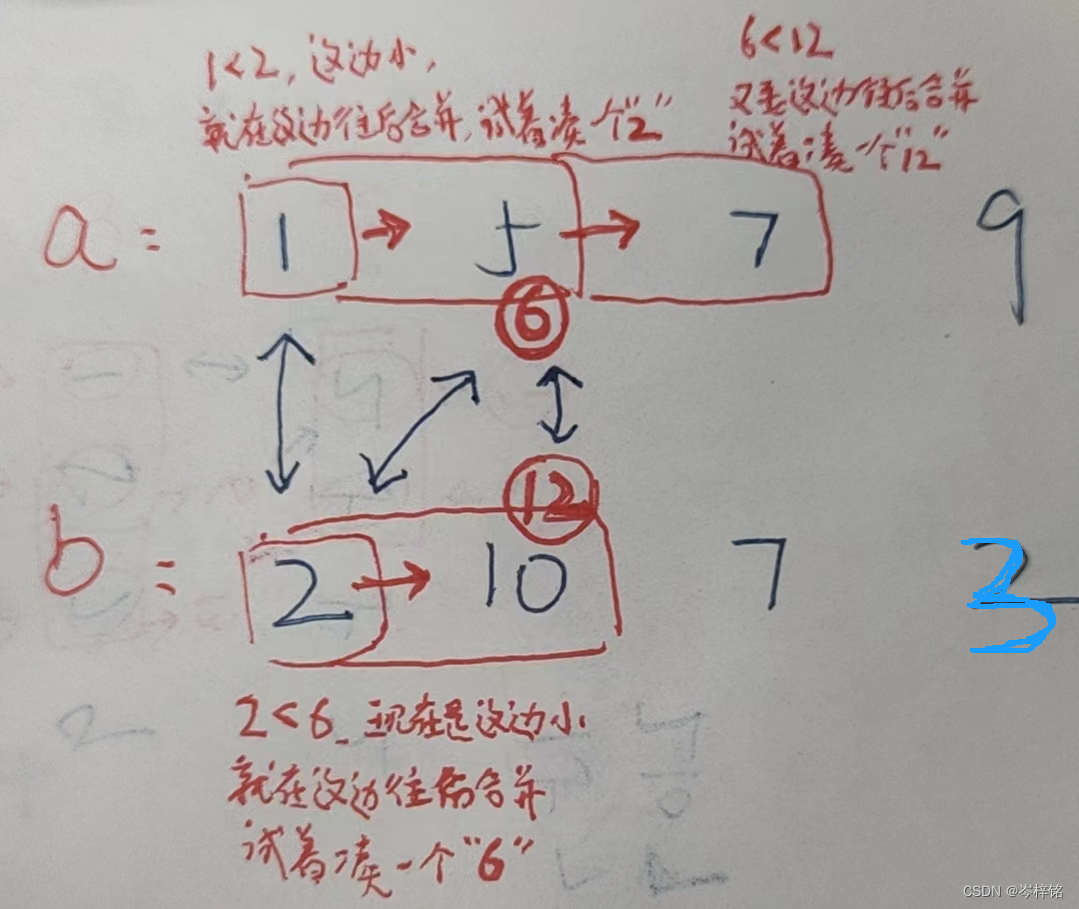
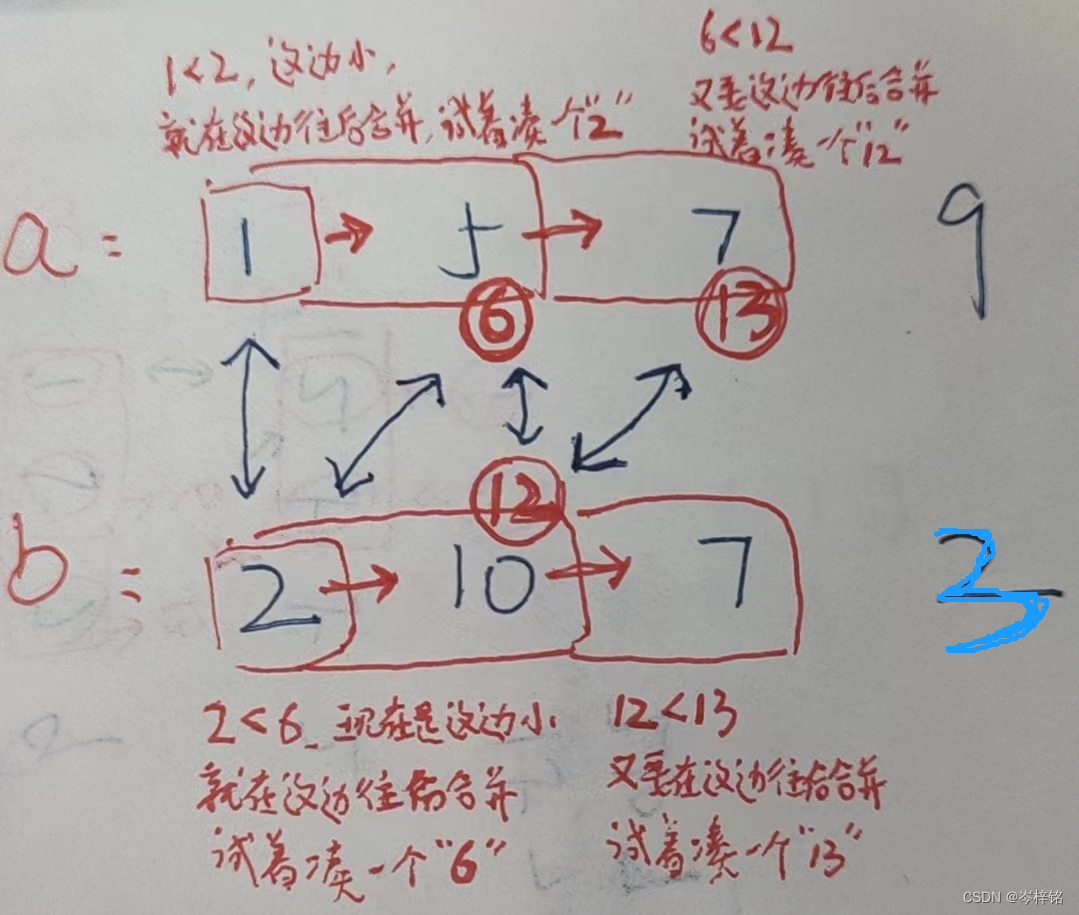
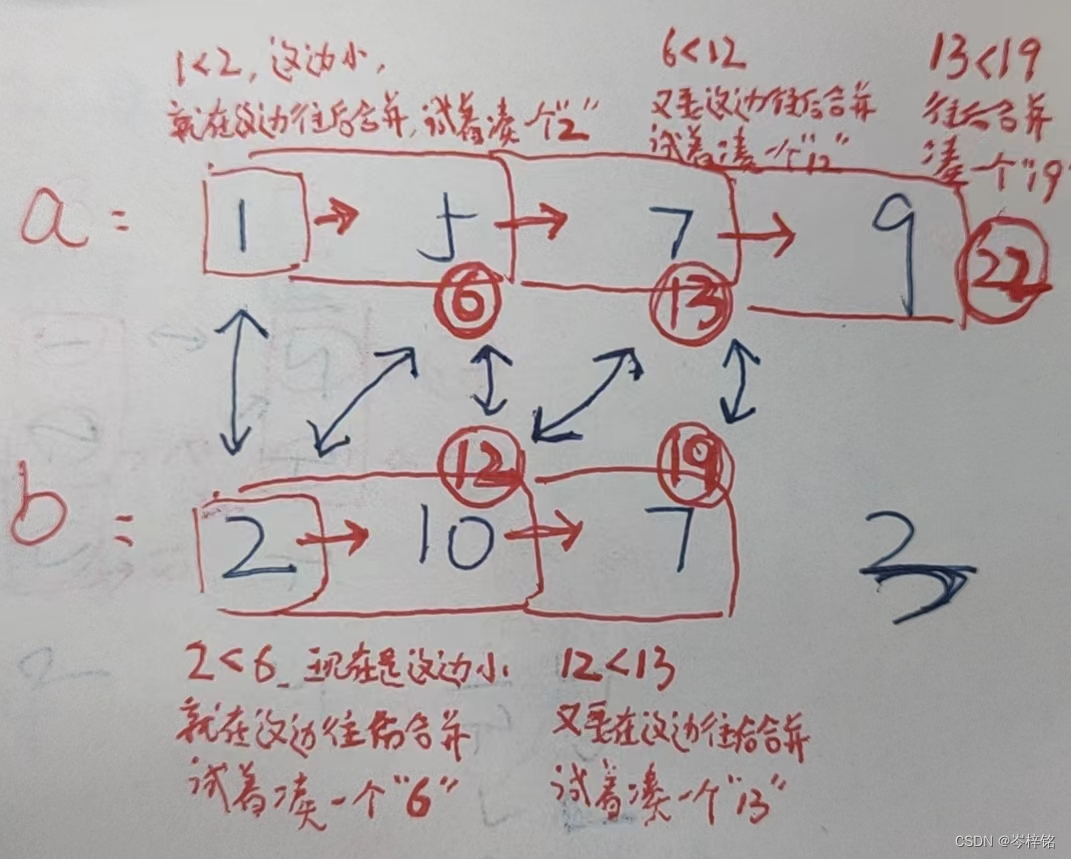
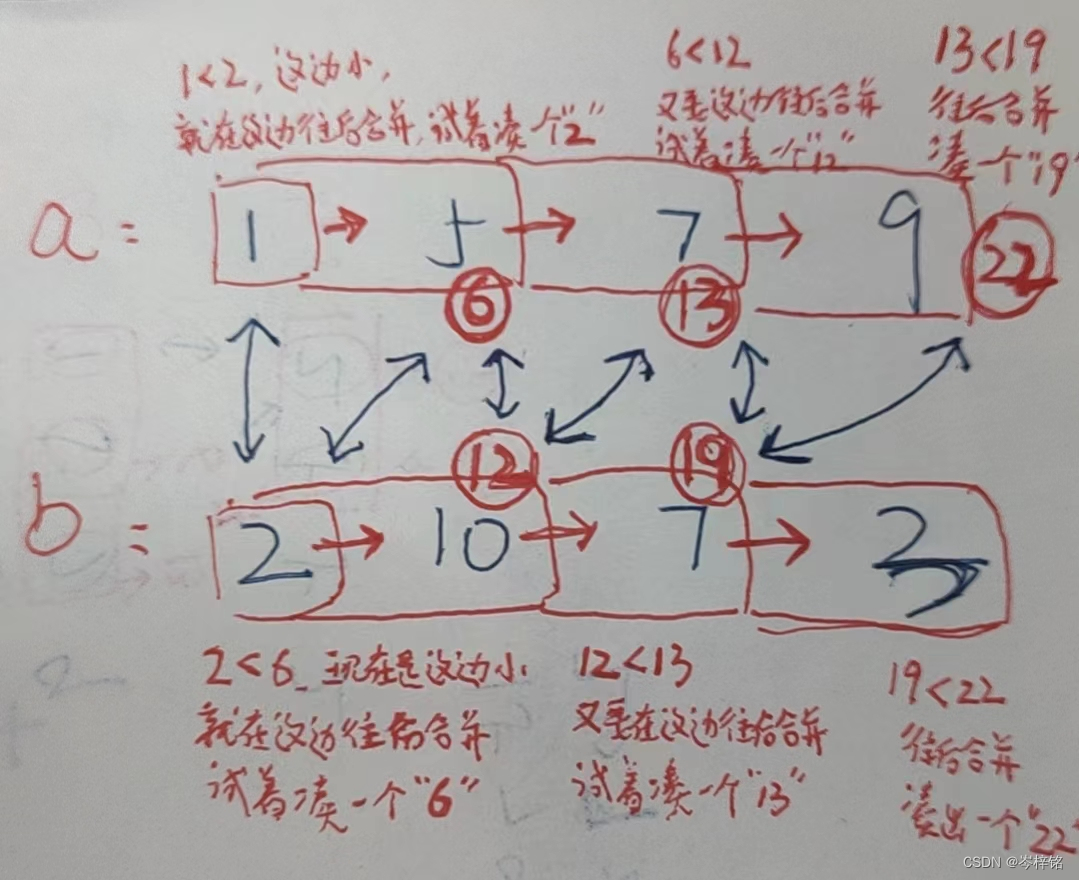
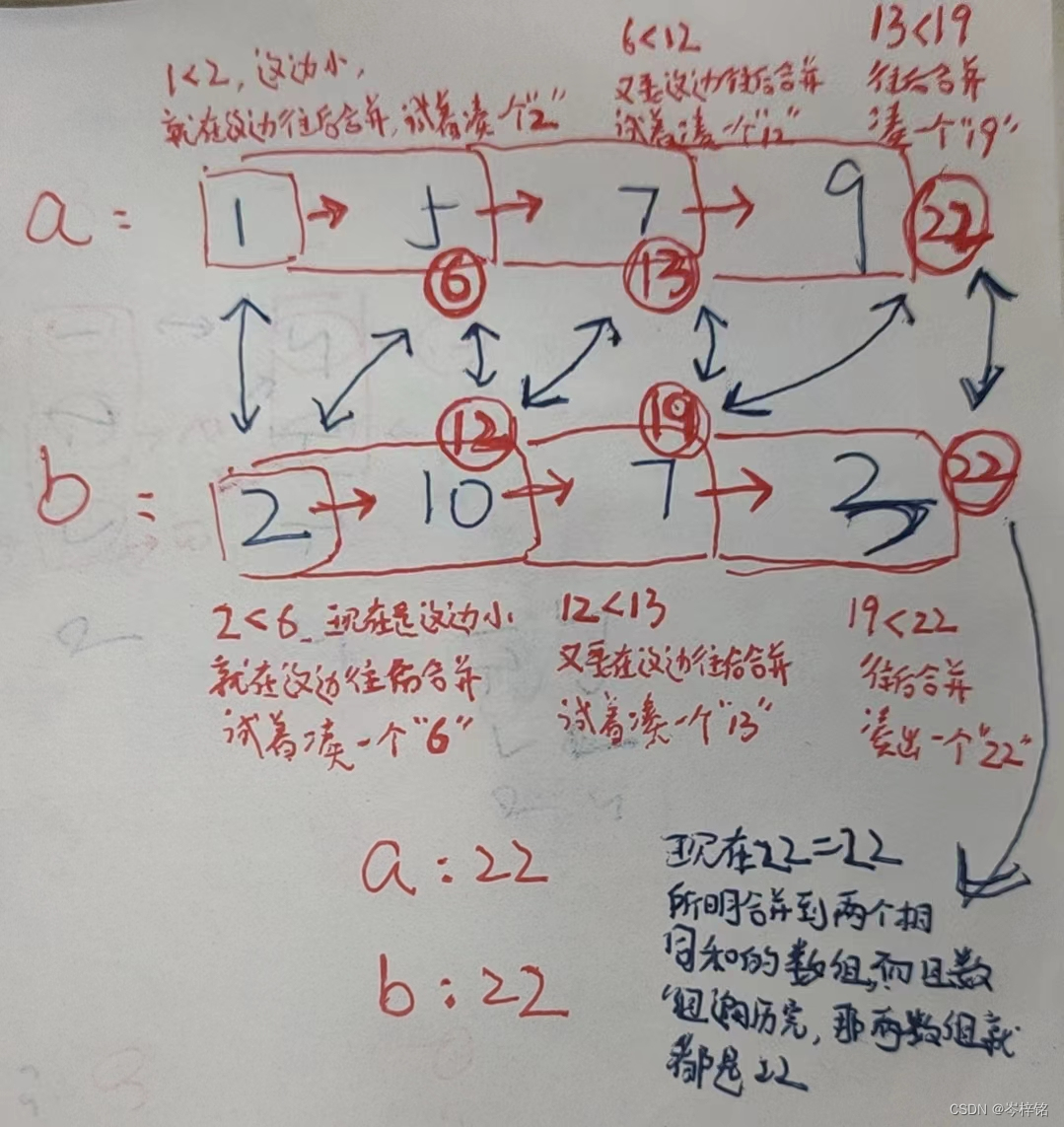
【当数组a前缀和等于数组b前缀和的时候,就说明已经在相同和的合并数组里了】
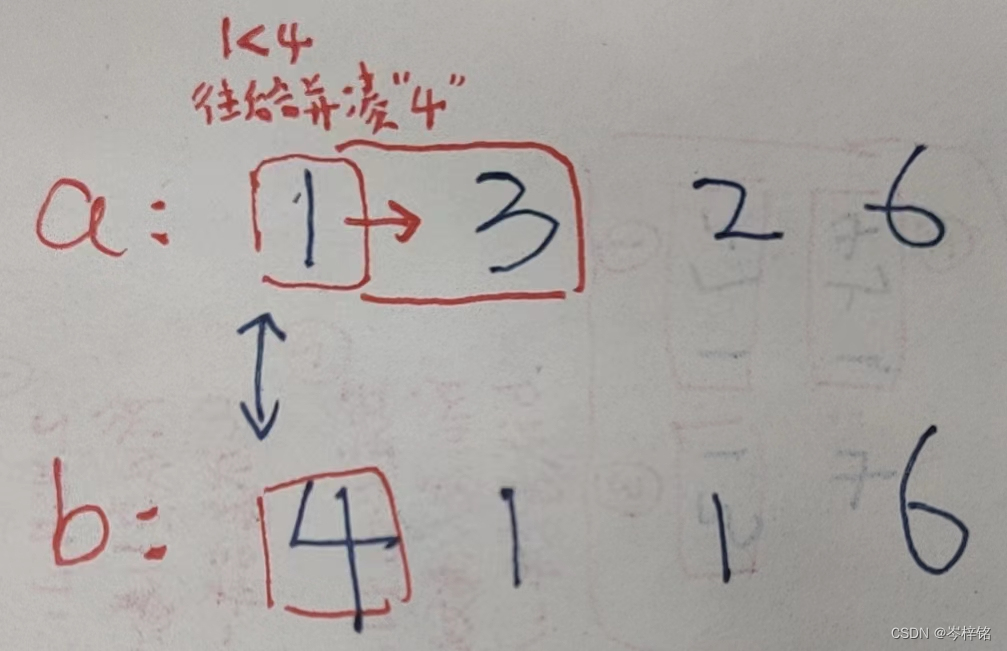
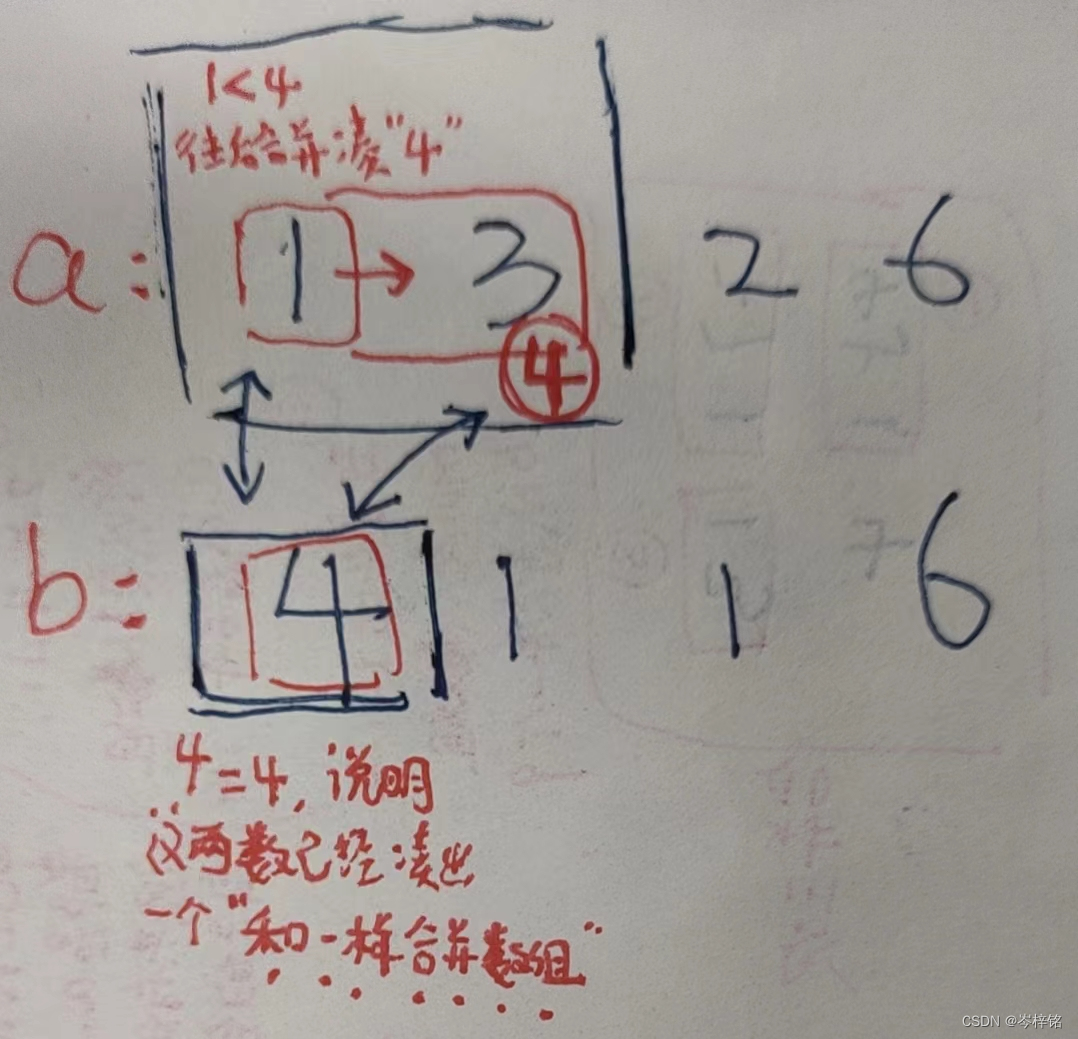
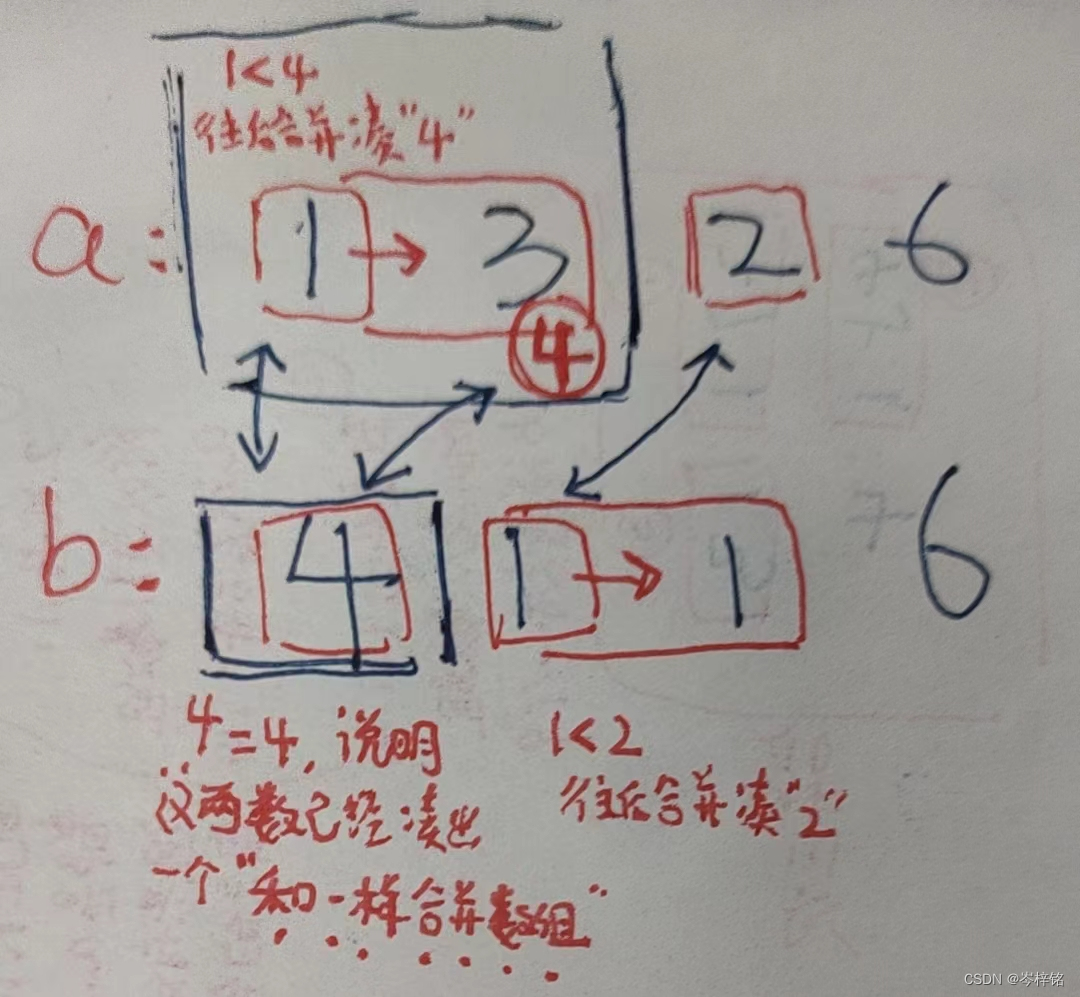
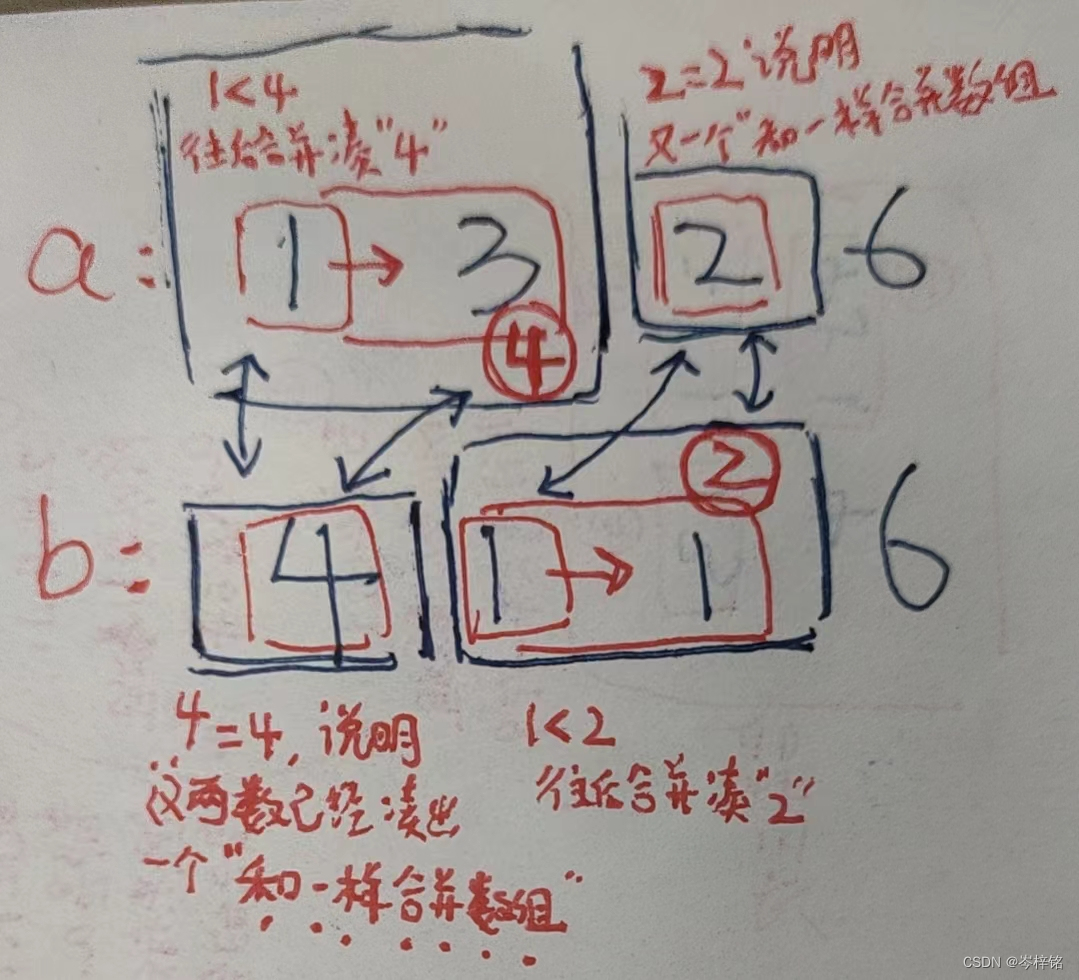
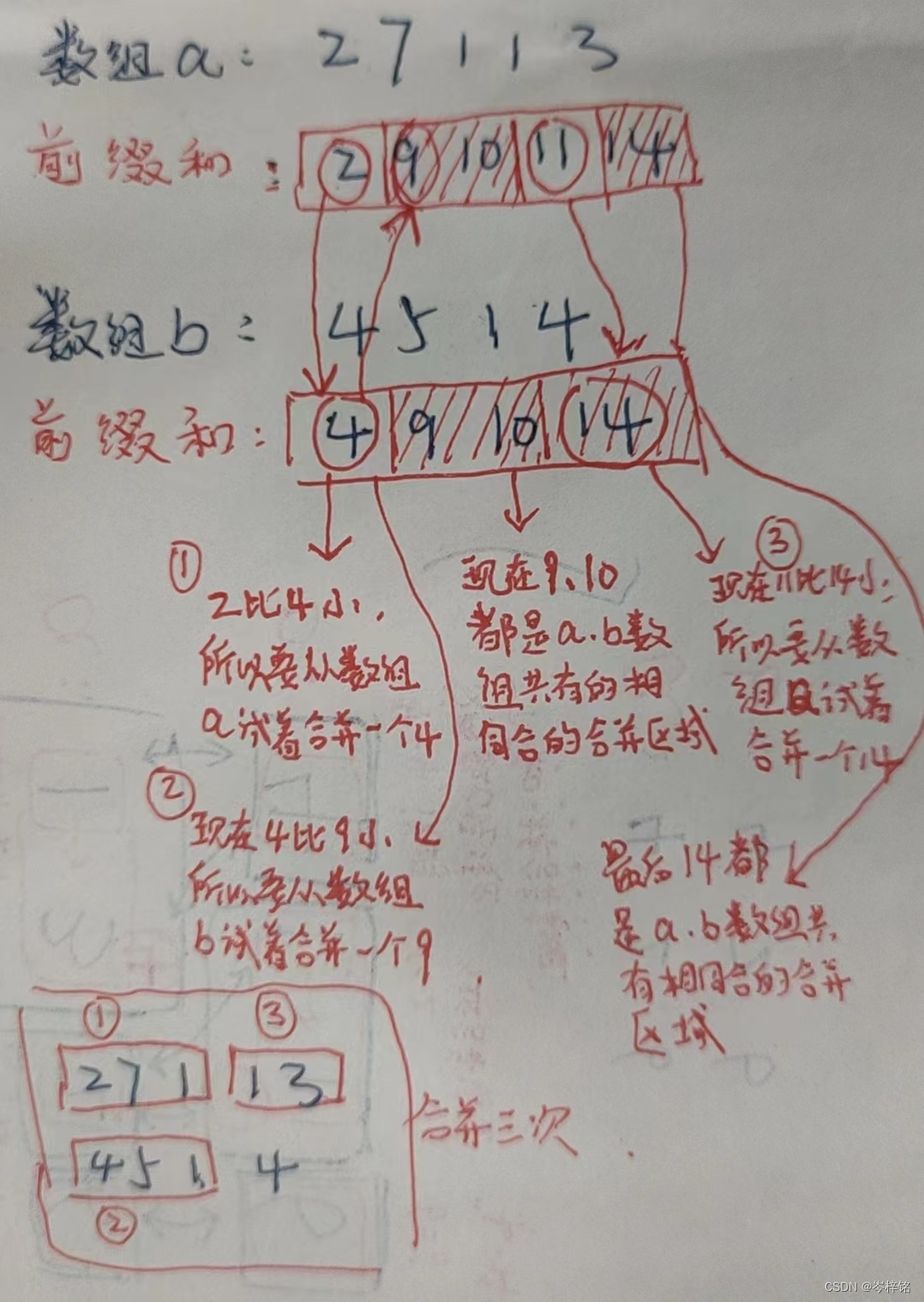
那么规律简单来说就是:得出两个前缀和数组,然后两个指针分别遍历数组,前缀和一样的时候 啥也不用管、双指针同时往后遍历;前缀和不一样的时候,谁小就指针往谁后遍历(合并数组),并统计【合并次数+1】;
完整代码:
java
import java.util.Queue;
import java.util.Scanner;
public class 国赛_合并数列 {
public static void main(String[] args){
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int m = in.nextInt();
//装两个数组,这里数组长度多+1,是为了空出第0位方便前缀和计算
int[] a = new int[n+1];
int[] b = new int[m+1];
//这两个数组是前缀和数组,这里数组长度多+1,是为了空出第0位方便前缀和自己计算
int[] a_ans = new int[n+1];
int[] b_ans = new int[m+1];
for (int i = 1; i < n+1; i++) {
a[i] = in.nextInt();
//前缀和成员等于原数组每一个成员累计加后面的成员
a_ans[i] = a_ans[i-1]+a[i];
}
for (int i = 1; i < m+1; i++) {
b[i] = in.nextInt();
//前缀和成员等于原数组每一个成员累计加后面的成员
b_ans[i] = b_ans[i-1]+b[i];
}
//index1是遍历a的前缀和数组的"指针"
int index1 = 1;
//index2是遍历b的前缀和数组的"指针"
int index2 = 1;
//count是统计【最少合并次数】的
int count = 0;
while (index1 < a_ans.length && index2 < b_ans.length){
if (a_ans[index1] == b_ans[index2]) { //前缀和相同的时候就说明就在合法的合并区域内,啥也不用管,直接同时往后遍历
index1++;
index2++;
} else if (a_ans[index1] < b_ans[index2]) { //前缀和不一样的话,谁小就让谁往后合并数组,并且要统计当前合并了一次数组
count++;
index1++;
} else {
count++;
index2++;
}
}
System.out.println(count);
}
}二、蓝桥杯不知第几届编程题:数等腰三角(史诗级顶级难)

【思路】:直角坐标系公式、排列组合、哈希表、枚举
1、思路一
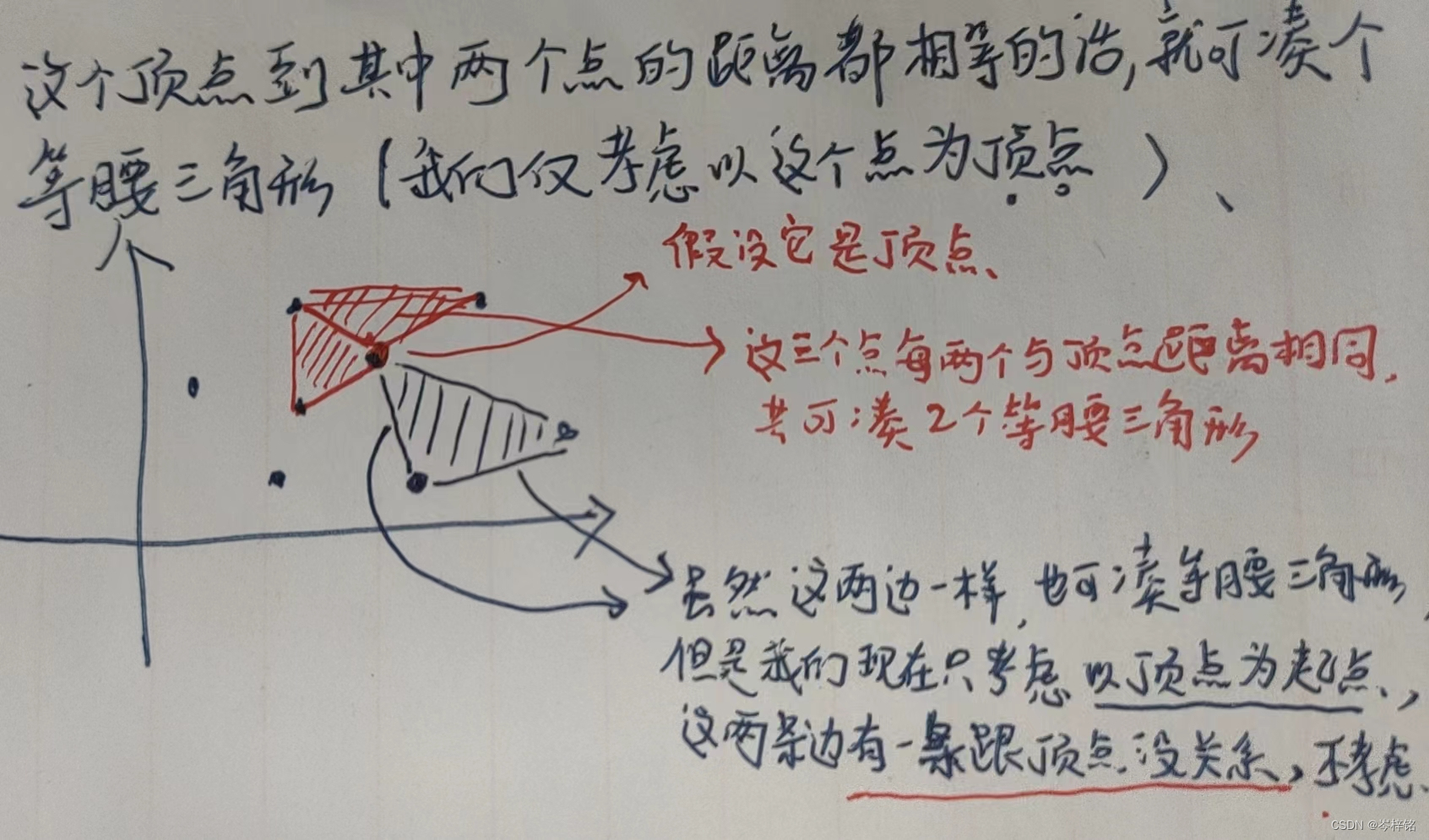
首先我们遍历所有的点(x , y) ,每遍历到一个点,就以这个点为三角形的顶点 ,这个顶点到其中两个点的距离都相等 的话,就可以凑一个等腰三角形
(注意!我们仅考虑以这个点为顶点来凑等腰三角形)
提一下距离公式:
但是因为开根号要涉及到浮点数,那既然只是用来比较距离,d的平方也可以,那就去掉根号
2、思路二
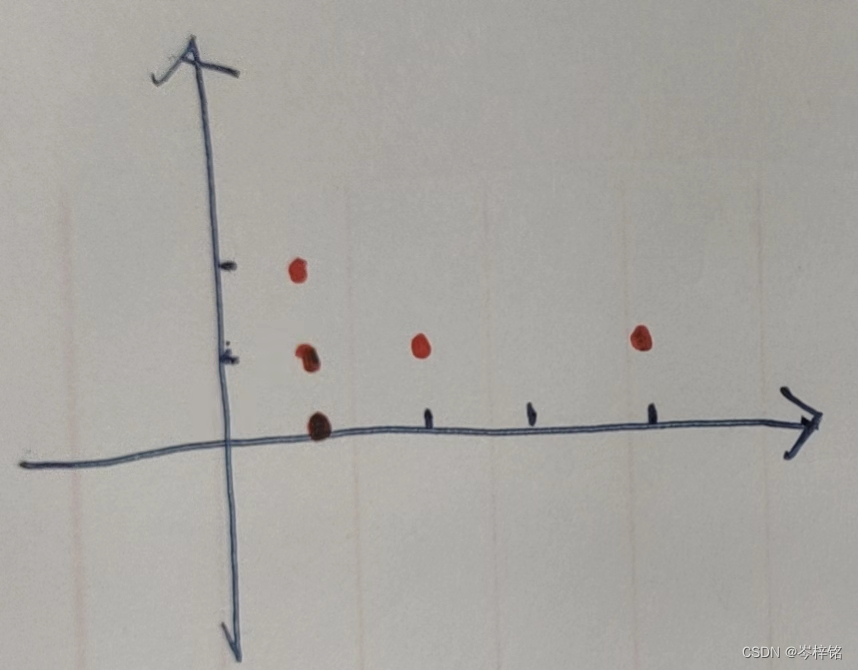
但不是直接数有几条距离相等的边就能确定能凑出几个三角形的,这样不准、而且效率也不高,例子:
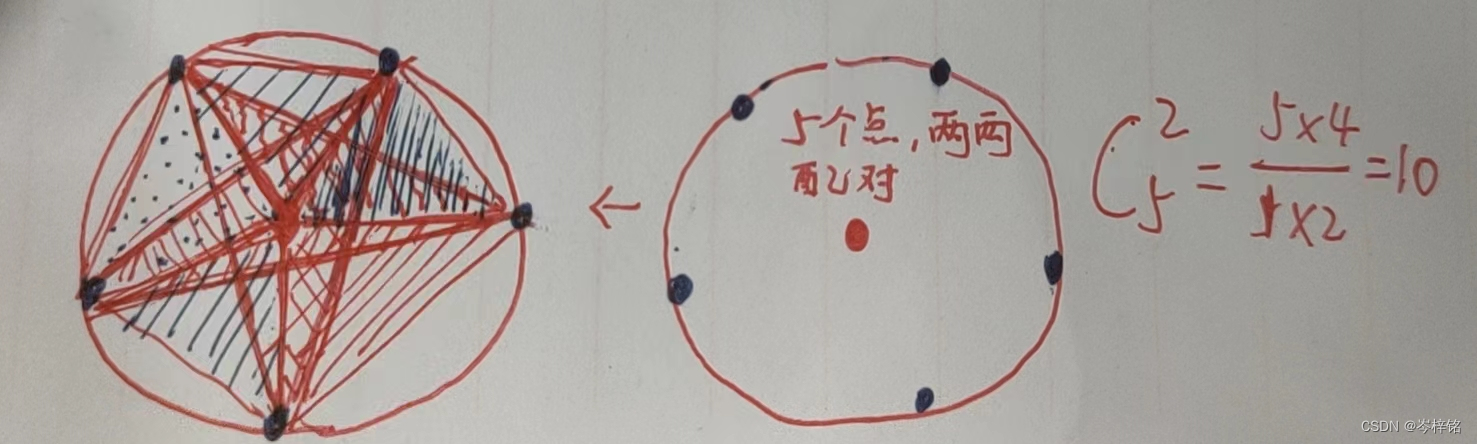
那么要知道:★一个圆内,圆心到圆弧上任意一点距离相等
那么我们就可以分类,把顶点距离相同的这些点归为一类 ,凑成 "一个圆"
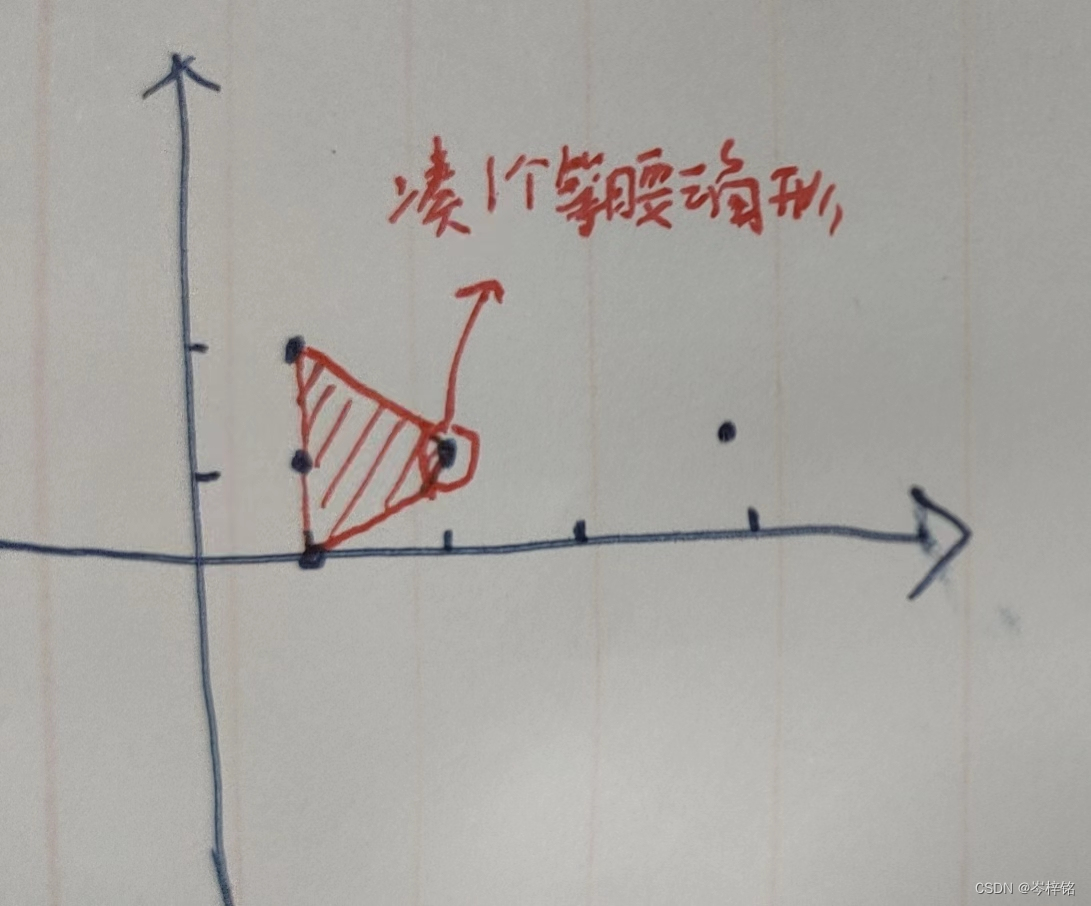
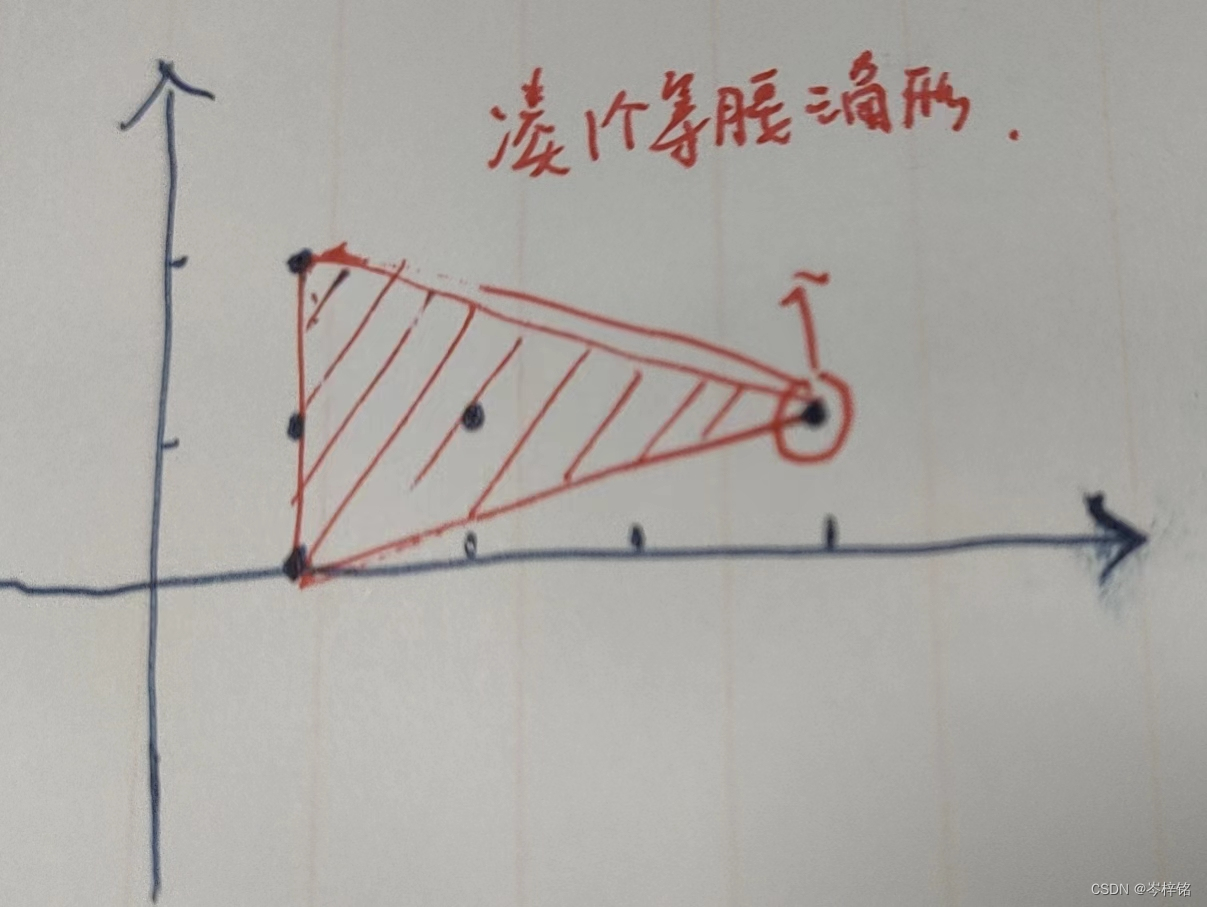
然后在这个圆里,圆心与2个点可凑一个等腰三角形,几个点里两个点凑一组有几种可能?这不就是排列组合吗
3、留意点
但是还要考虑到特殊情况:三点共线
如果是三点共线 的话,即使这两个点距离圆心距离一样 ,也不能凑成等腰三角形,普通三角形都凑不成。
那么再遍历圆弧上所有的点,每遍历到一个点(x2 , y2),根据下面这个公式,求出跟它共线的点
当求出这个跟它共线的**点(x3 , y3)**之后,运用 "哈希表" 标记这个点是个【不合法点 】,有几个【不合法点】就表示出现了几次三点共线情况。
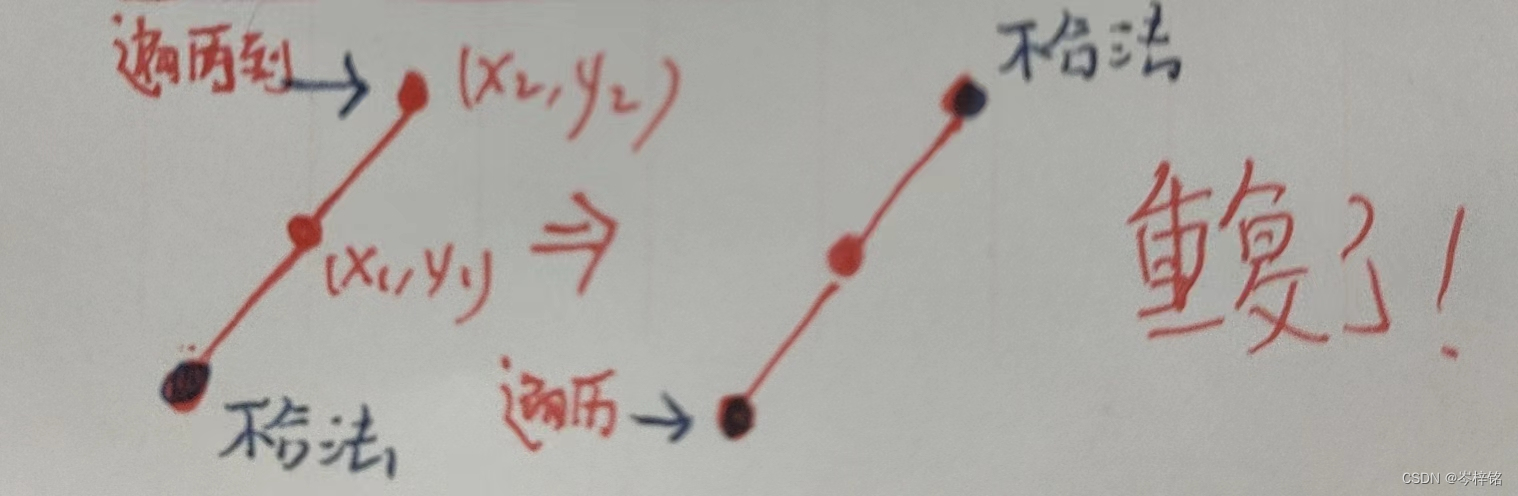
但是还要注意这两个点在一个线上,当以点(x2 , y2)求共线点时会标记点(x3 , y3)
而当以点(x3 , y3)求共线点时,又会标记点(x2 , y2) 为【不合法点】
但是这就重复标记了两次这个直线三点共线的情况
所以三点共线****的情况次数 应该是【不合法点 / 2】
4、总结公式
那么一个"圆"里的n个圆弧点可以凑几个三角形:
- (不合法点 / 2)
那么最后以某一个点为三角形的顶点时,可以凑出几个等腰三角形就是:距离各个其他点的凑成的各个"圆"里可以凑几个三角形相加
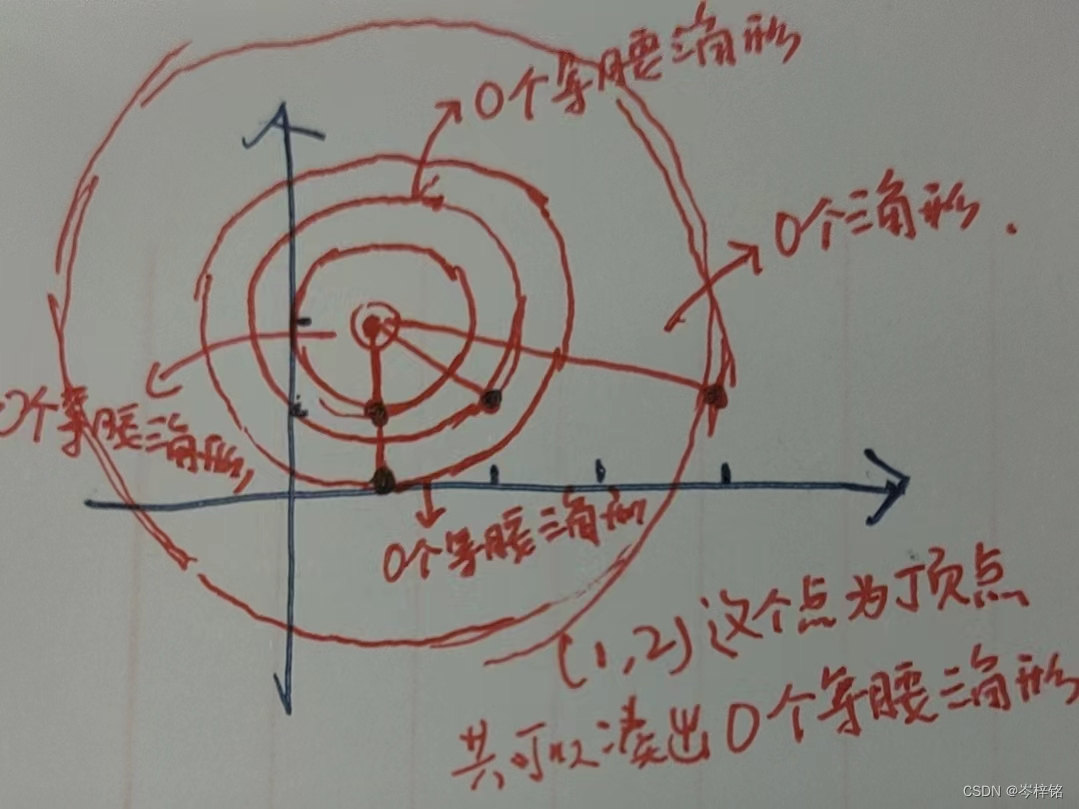
最后一个二维坐标系里这些点可以组成几个等腰三角形:枚举所有点为顶点时可以凑几个等腰三角形,然后相加,看下面一个例子
所以最后总共可以凑4个等腰三角形
完整代码:
我自己的(我乏了,我一点做不出来,我花了整整一天时间证明了自己的智商有限,答案是错误的,希望有牛逼的大佬指出我的代码的问题所在)
java
import java.util.*;
public class 数等腰三角形 {
public static void main(String[] args){
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int[][] point = new int[n][2];
Map<int[],Integer> Point = new HashMap<>();
//输入所有点的坐标
for (int i = 0; i < n; i++) {
point[i][0] = in.nextInt();
point[i][1] = in.nextInt();
Point.put(new int[]{point[i][0],point[i][1]} , 1);
}
//哈希表记录每一个顶点(圆心)的相同距离的边的点的坐标
Map<Integer, ArrayList<int[]>> map = new HashMap<>();
//统计总共有多少等腰三角形
int count = 0;
//枚举所有点,遍历到一个,就以他为顶点(圆心)
for (int i = 0; i < point.length; i++) {
//获取顶点坐标
int vertexX = point[i][0];
int vertexY = point[i][1];
//遍历除了顶点(圆心)以外的其他所有点
for (int j = 0; j < point.length; j++) {
if( i != j ){
//记录下当前这个外围点坐标
int x2 = point[j][0];
int y2 = point[j][1];
//计算距离,并记录这个距离有一条边(circlePoint数组当前下标 +1)
int d = (int)(Math.pow(vertexX-x2,2) + Math.pow(vertexY-y2,2));
//然后记录下
int[] circlePoint = {x2, y2};
ArrayList<int[]> list = map.getOrDefault(d,new ArrayList<>());
list.add(circlePoint);
map.put(d , list);
}
}
//超级超级重要!!!哈希表遍历方法
for (Map.Entry<Integer, ArrayList<int[]>> entry : map.entrySet()) {
int key = entry.getKey(); // 获取键
ArrayList<int[]> list = entry.getValue();
int sum = list.size();
count += sum * (sum-1) / 2;
int del = 0;
for (int j = 0; j < list.size(); j++) {
int x2 = list.get(j)[0];
int y2 = list.get(j)[1];
int x3 = 2 * vertexX - x2;
int y3 = 2 * vertexY - y2;
del += Point.getOrDefault(new int[]{x3, y3},0);
}
count -= (del / 2);
}
map.clear();
}
System.out.println(count);
}
}别人的C++正确代码
cpp
#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main(){
int n; cin >> n;
vector<array<int,2>>a(n);
map<pair<int,int>, int>node;
for(int i = 0; i < n; i ++) {
cin >> a[i][0] >> a[i][1];
node[{a[i][0], a[i][1]}] ++;
}
int ans = 0;
for(int i = 0; i < n; i ++) {
map<int,vector<int>>st;
for(int j = 0; j < n; j ++) {
int dis = (a[i][0] - a[j][0]) * (a[i][0] - a[j][0]) + (a[i][1] - a[j][1]) * (a[i][1] - a[j][1]);
if(dis)st[dis].push_back(j);
}
for(auto x: st) {
vector<int>&no = x.second;
int sum = no.size();
ans += sum * (sum - 1) / 2;
int del = 0;
for(int j = 0; j < no.size(); j ++) {
int x1 = a[i][0], y1 = a[i][1];
int x2 = a[no[j]][0], y2 = a[no[j]][1];
int x3 = x1 * 2 - x2, y3 = y1 * 2 - y2;
del += (node[{x3, y3}]);
}
ans -= (del / 2);
}
}
cout << ans << endl;
return 0;
}还有别人正确的java代码
cpp
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
List<int[]> a = new ArrayList<>();
Map<String, Integer> node = new HashMap<>();
for(int i = 0; i < n; i ++) {
int x = sc.nextInt();
int y = sc.nextInt();
a.add(new int[]{x, y});
String no = x + "#" + y;
node.put(no, node.getOrDefault(no, 0) + 1);
}
long ans = 0;
for(int i = 0; i < n; i ++) {
Map<Long, List<Integer>> st = new HashMap<>();
for(int j = 0; j < n; j ++) {
int x1 = a.get(i)[0], y1 = a.get(i)[1];
int x2 = a.get(j)[0], y2 = a.get(j)[1];
long dis = (long)Math.pow(x1 - x2, 2) + (long)Math.pow(y1 - y2, 2);
if(dis == 0)continue;
if(st.get(dis) == null)
st.put(dis, new ArrayList<Integer>());
st.get(dis).add(j);
}
for(Map.Entry<Long, List<Integer>> x: st.entrySet()){
List<Integer>no = x.getValue();
long sum = no.size();
ans += sum * (sum - 1) / 2;
long del = 0;
for(int j = 0; j < no.size(); j ++) {
int x1 = a.get(i)[0], y1 = a.get(i)[1];
int x2 = a.get(no.get((j)))[0], y2 = a.get(no.get((j)))[1];
int x3 = x1 * 2 - x2, y3 = y1 * 2 - y2;
if(node.get(x3 + "#" + y3) != null)
del += node.get(x3 + "#" + y3);
}
ans -= del / 2;
}
}
System.out.println(ans);
}
} }
}死臭咯这下,希望尽快有人能找出我最后一题代码的问题