1. 研究背景及意义
近年来,随着我国科技和经济高速发展,人们生活质量也随之显著提高。但是, 环境污染问题也日趋严重,给人们的生活质量和社会生产的各个方面都造成了许多不 利的影响。空气污染作为环境污染主要方面,更是严重危害着人们身体健康,为有效地改善人们生活环境,开展大气污染防治工作刻不容缓。
空气污染影响因素有很多,如工厂废气、汽车尾气的排放等。除此之外,不同的 地理区域对于空气污染也有着不同的影响,例如冬季北方的空气质量普遍较差等。现研究中对于空气污染状况的衡量指标有两类,分别是单个指标和综合指标。单个指标包括PM2.5,PM10,CO,SO2,NO2,O3六种污染物。综合指标有空气污染指标(API) 和空气质量指标(AQI)。API只统计了NO2,PM10,SO2三种污染物,而AQI是统计 了六种污染物,相比较API可以更为准确地概述空气质量状况。
2.研究现状
关于空气质量指数的影响因素,直观上是空气中六种污染物浓度。但是空气污染 是一个复杂的现象,污染物浓度的变化会受到许多因素的影响。一方面是污染物排放 影响,如车辆尾气排放,工业生产中废气排放,垃圾焚烧和居民取暖等。另一方面受 当地地形地貌、人口发展密度及气象条件等影响。相关因素对空气质量影响强度的评估也有许多方法,最常见的有图表相关分析,协方差及协方差矩阵,相关系数及互信 息数等等。....
3.本文数据介绍
本文所运用到的数据来源于全球暖化数据集中世界主要国家空气污染指数表(年)的数据,本文主要是针对芬兰的空气污染指数进行分析和预测,在处理数据时,将特征进行了筛选,最终选择了氮氧化物、PM2.5、PM10等特征,原始数据展示如下:
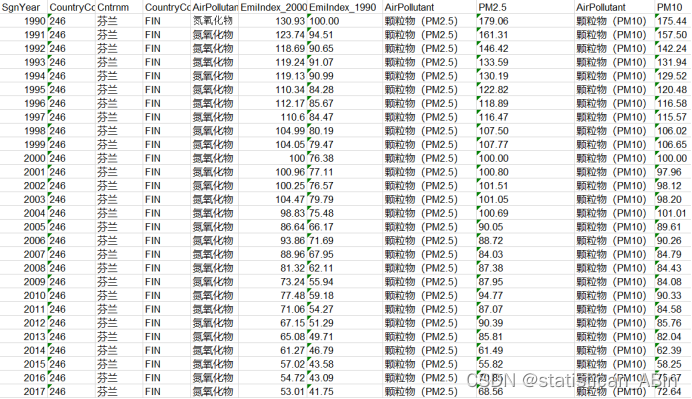
4.数据展示和模型构建
首先,读取数据,查看数据属性:
R
library(openxlsx)
# 文件名+sheet的序号
KQWR_data<- read.xlsx("芬兰空气污染.xlsx", sheet = 1)
View(KQWR_data)
KQWR_data
summary(KQWR_data)#####描述性统计分析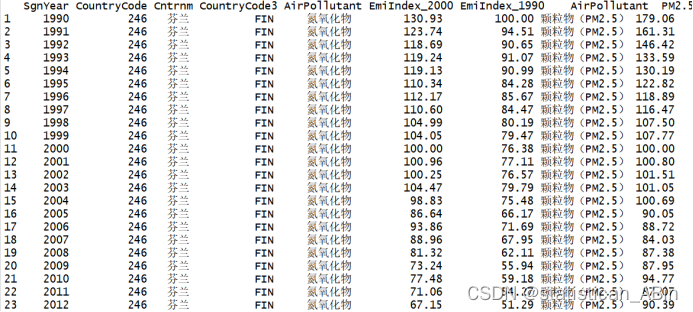
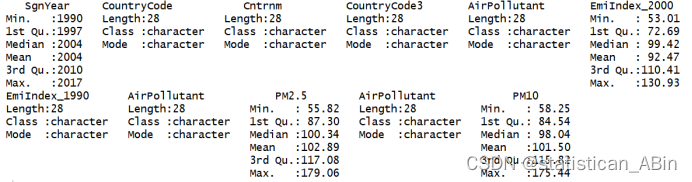
从图三可以看出,对数据进行了描述性统计,其中氮氧化物的最小值为53.01,最大值为130.93,PM2.5的最小值为55.82,最大值为175.44,PM10指数的最小值为58.25,最大值为175.44。接下来分别画出指标的条形图
R
###氮氧化物
KQWR_Emi<-KQWR_data$EmiIndex_2000
KQWR_Emi
barplot(KQWR_Emi,xlab="年份",ylab="排放指数",col="pink",main="氮氧化物排放指数",border="blue")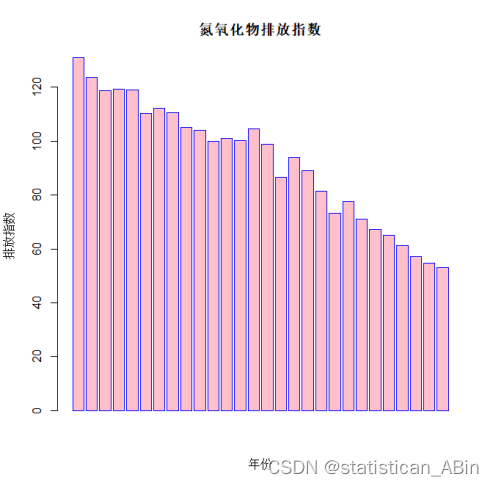
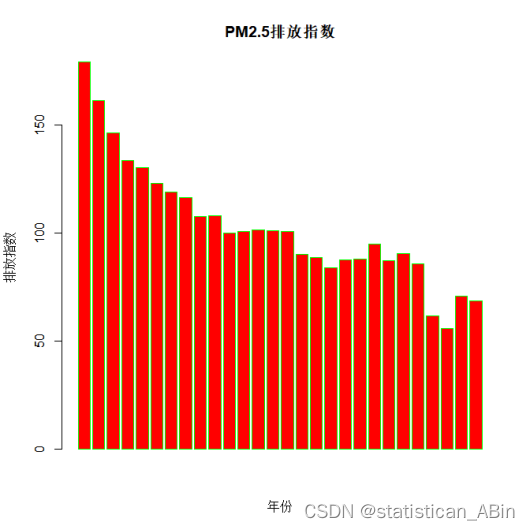
从上面三个指标的条形图可以看出,氮氧化物、PM2.5以及PM10随着时间的变化但是在逐步下降,这也归功于世界各地的节能减排措施的执行,虽然PM2.5和PM10在后几年有小幅的上升但是总体趋势还是逐渐下降的。随后画出氮氧化物的时序图,如下:
R
###氧化物时间序列图
KQWR_Emi
TS_KQWR_Emi<-ts(KQWR_data$EmiIndex_2000,start=c(1990),frequency=1)
TS_KQWR_Emi
plot(TS_KQWR_Emi,type="o",pch=20,main="时间序列图",xlab = "年份/Y",ylab="气温",col = "yellow")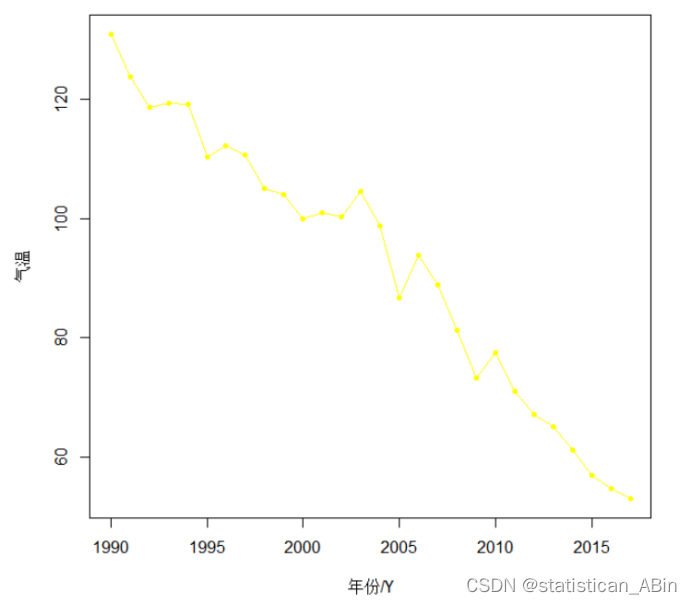
在可视化之后,随后进行模型的构建,但是在构建模型之前,还需要对序列数据进行纯随机性检验,具体结果如下:


画出该序列的自相关和偏自相关图
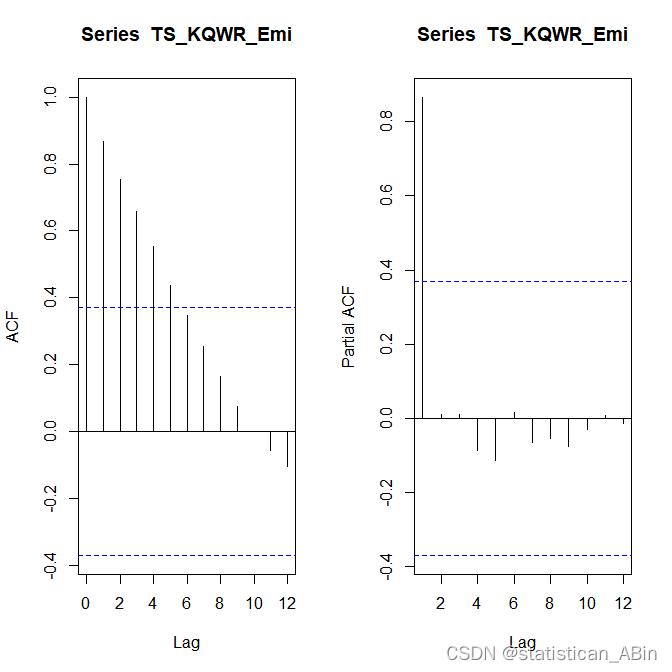
随后进行ADF检验
R
#ADF检验
library(aTSA)
adf.test((TS_KQWR_Emi)) 
随后进行定阶处理,下面进行自动定阶的函数,计算得到模型应该采用ARIMA(0,1,1),拟合得到模型系数

随后查看序列的正态分布情况:
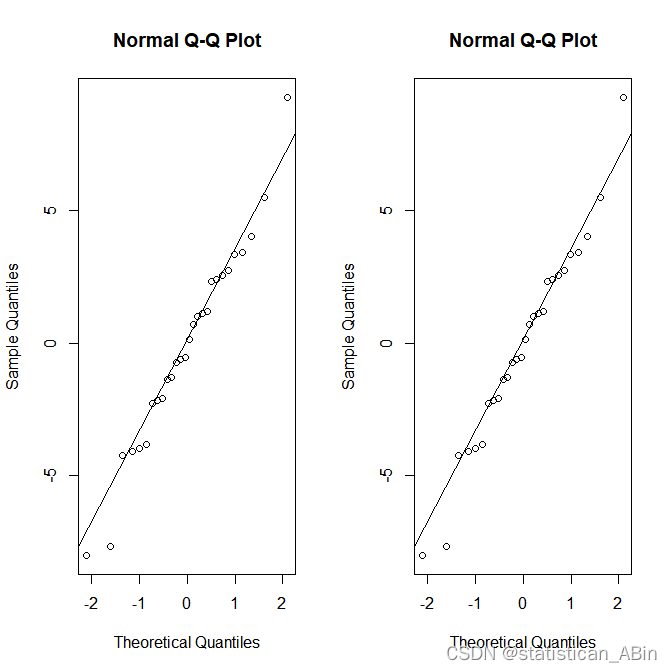
下面进行模型的残差检验:
R
###残差检验
Box.test(TS_KQWR_Emi.fit $residuals,type = "Ljung-Box")
从残差结果显示,P值为0.8188,显然大于0.05,故在显著性水平5%下,没有理由拒绝原假设。说明残差是白噪声。接下来进行最终的预测,本文预测h=5,表明预测5年芬兰的空气污染指数(氮氧化物)的污染指数,具体结果如下:

5.结论
本文对数据进行了预处理以及相关分析。首先,对数据进行了数据指标的整合处理,保证模型可以更好地对数据进行学习。其次,对原始数据进行可视化并分析其趋势,随后在建模前进行相应的检验工作,最终进行建模分析,发现RIMA模型对于单一序列的线性拟合效果较好.....
创作不易,希望大家多多点赞收藏和评论!