105. 从前序与中序遍历序列构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

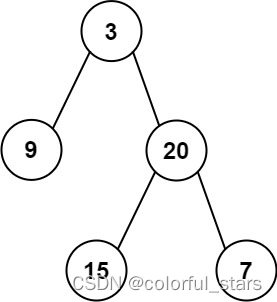
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均无重复元素
inorder 均出现在 preorder
preorder 保证为二叉树的前序遍历序列
inorder 保证为二叉树的中序遍历序列

分治法（递归）
算法描述 ：

1、根据前序序列根节点在中序序列中的索引，划分左右子树的边界；

2、经过递归，依次获得左右子树；

算法流程 ：

root：前序遍历中根节点索引

left：中序遍历子树的左边界节点索引

right：中序遍历子树的右边界节点索引

终止条件 ：

left > right ，此时越界；

递推体：

1、建立根节点；

2、根据前序序列根节点在中序序列中的索引，划分左右子树的边界；

3、对左右子树进行递归；

cpp 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        preorderp = preorder;
        for (int i = 0; i < inorder.size(); i++)
            dic[inorder[i]] = i;
        return recursion(0,0,inorder.size()-1);
    }
private:
    unordered_map<int, int> dic;//索引字典
    vector<int> preorderp;

    //root：根节点索引
    //left：左边界节点索引
    //right：右边界节点索引
    TreeNode *recursion(int root, int left, int right) {
        if (left > right) return nullptr;//终止条件
        TreeNode *node = new TreeNode(preorderp[root]);//根节点
        int i = dic[preorderp[root]];//根据前序序列根节点在中序序列中的索引，划分左右子树的边界
        int left_tree_len = i - left;//左子树长度
        // cout << "左子树长度为：" << left_tree_len << endl;
        //（root + left_tree_len + 1）：相对于当前根索引的偏移量
        node->left = recursion(root + 1, left, i - 1);
        node->right = recursion(root + left_tree_len + 1, i + 1, right);
        return node;
    }
};

注意：
root + left_tree_len + 1表示为：前序遍历中，右子树根节点的索引

即：当前根节点索引+左子树长度+1

左子树长度left_tree_len 为：根节点在中序序列中的索引-左边界