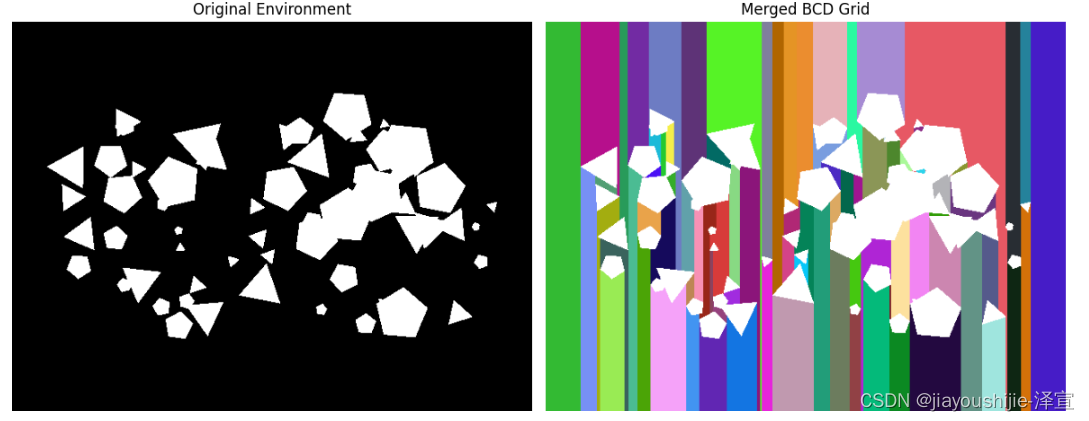
2000年一篇论文 Coverage of Known Spaces: The Boustrophedon Cellular Decomposition 横空出世,解决了很多计算机和机器人领域的覆盖路径问题,今天我来详细解读这个算法。
The Boustrophedon Cellular Decomposition 算法详解
这篇论文标题为"Coverage Path Planning: The Boustrophedon Cellular Decomposition",是由Howie Choset和Philippe Pignon发表。
Abstract
Coverage path planning is the determination of a path that a robot must take in order to pass over each point in an environment. Applications include vacuuming, floor scrubbing, and inspection. We developed the boustrophedon cellular decomposition, which is an exact cellular decomposition approach, for the purposes of coverage. Each cell in the boustrophedon is covered with simple back and forth motions. Once each cell is covered, then the entire environment is covered. Therefore, coverage is reduced to finding an exhaustive path through a graph which represents the adjacency relationships of the cells in the boustrophedon decomposition. This approach is provably complete and Experiments on a mobile robot validate this approach.
1 引言
覆盖路径规划确定了一条路径,保证了代理(agent)会经过给定环境中的每一个点。这个过程有多种应用。海军应用包括水雷反制任务和大陆架海洋测绘。商业应用包括污染清理、地板清洁、农作物犁地和桥梁检查。没有覆盖算法,这些应用就无法处理。目前大多数覆盖路径规划器充其量只是初级的,因为它们基于启发式方法。在扫雷中使用这种方法,就像用有故障的探雷器进行扫雷一样。因此,本文描述的覆盖路径规划算法是完备的;也就是说,在有限时间内,它将找到一条覆盖路径或确定不存在这样的路径。
我们的方法利用了一种称为精确Cell分解的几何结构,它是组成目标环境的非相交区域的并集。每个区域称为一个单元格,单元格的并集填充了整个环境。在每个单元格中,覆盖路径都可以很容易地确定,例如简单的来回运动;因此覆盖路径规划简化为规划从一个单元格到另一个单元格的运动。本文将开发一种新的Cell分解方法,称为Boustrophedon分解,并将其应用于覆盖路径规划。
Boustrophedon这个词在1699年首次在英语中使用,字面意思是"牛的方式"。通常,当牛在田地里拖犁时,它会沿着一条直线穿过整个田地,然后转身,沿着与前一条路径相邻的新直线路径前进。通过重复这个过程,牛保证覆盖(从而犁)整个田地。见图1。
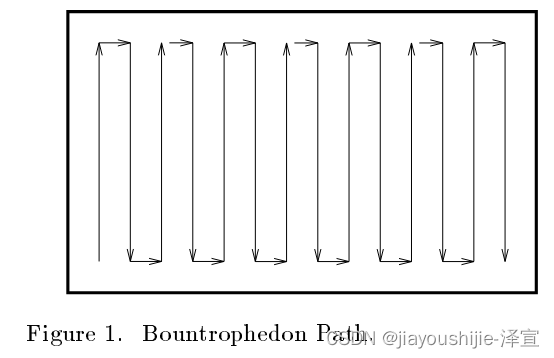
Boustrophedon Cell分解是一种新型的分解方法,其中机器人的自由空间被分解成单元格,使得机器人可以用来回的 boustrophedic 运动覆盖每个单元格。一旦机器人覆盖了每个单元格,它就覆盖了环境中的整个自由区域。这种方法已经通过仿真和 Nomadic 200 移动机器人基座进行了验证。
2 背景工作
2.1 覆盖的现有工作
覆盖的早期工作包括真空吸尘和地板清洁等应用。在这些方法中,必须将路径显式地编程到机器人中;也就是说,它们不使用算法来生成覆盖路径,而是"手工"规定一条路径。此外,这些算法依赖于部署在环境中的地标。
一些现代农业作业代表了覆盖路径易于自动生成的重要机会。Demeter项目用于收割大型农田;在这种方法中,机器人只是使用视觉来引导其路径,沿着先前割下的作物线,只能覆盖矩形田地。
考虑了非完整约束的地板覆盖方法。在这项工作中,一组模板用于仅覆盖没有障碍物的有界区域。这些模板用于适应机器人的非完整约束,因此可能有助于规划每个单元格内的来回运动。然而,其局限性在于它不能在存在障碍物时规划路径。
Zelinsky等人的覆盖算法非常适合非结构化环境。尽管它是完备的,但它在离散环境中实现了地板覆盖(即它是分辨率完备的)。Kurabayashi等人提出了一种类似的方法,没有证明,采用了合作机器人。最后,Lumelsky等人提出了一种与平面情况下提出的方法类似的算法。尽管提出的算法在平面情况下产生了与Lumelsky小组几乎相同的路径,但本文中描述的方法更易于实现,因为它只有两种情况,而他们的方法包含一系列特殊情况。最后,Hert等人的方法不是完备的。Hert等人提供的算法的主要贡献是它是增量的,因此可能导致在移动机器人上的基于传感器的实现。
2.2 精确Cell分解
本文中使用的覆盖方法是对现有完备运动规划方案的改编,称为精确Cell分解。Cell分解是一种运动规划技术,其中自由配置空间(机器人不与障碍物重叠的所有机器人配置的集合)被分解成单元格,使得单元格的并集是原始自由空间。每个单元格可以表示为图中的一个节点,相邻单元格在它们对应的节点之间有一条边。这个图称为邻接图。如果机器人可以覆盖每个单元格,那么地板覆盖问题就简化为确定访问每个节点至少一次的邻接图遍历,即旅行商问题,对于旅行商问题总是存在解(可能是次优的)。
一种流行的Cell分解技术是梯形分解(也称为条带法),它可以产生完备的覆盖路径解。在梯形分解中,机器人的自由空间被分解成梯形单元格。由于每个单元格都是梯形,因此可以通过简单的来回运动轻松实现每个单元格的覆盖(见图1)。通过访问邻接图中的每个单元格来实现对环境的覆盖。
梯形分解方法假设一条垂直线段(称为slice)从左到右扫过由多边形障碍物填充的有界环境。单元格是通过一系列打开和关闭操作形成的,当slice遇到一个事件时,事件是slice与多边形顶点相交的实例。有三种类型的事件:IN、OUT和MIDDLE。粗略地说,在IN事件中,当前单元格关闭(从而完成其构造),两个新单元格打开(从而启动其构造)(图2)。OUT事件正好相反:两个单元格关闭,一个新单元格打开(图3)。IN事件可以看作是一个单元格分解成两个单元格,而OUT事件是两个单元格合并成一个单元格。在MIDDLE事件中,当前单元格关闭,一个新单元格形成。这些操作的结果是自由空间被分解成梯形单元格。
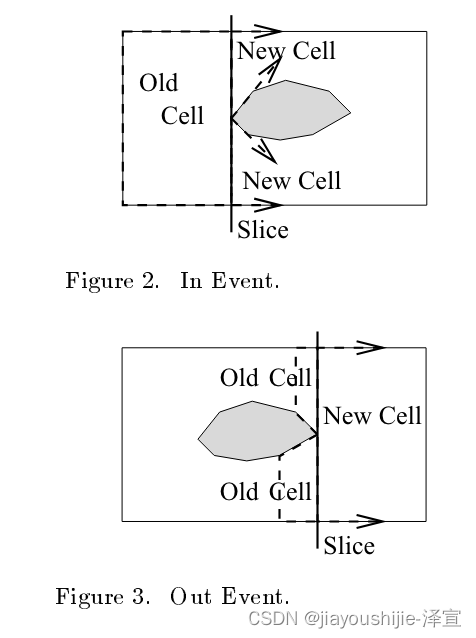
VanderHeide和Rao的地形覆盖系统基于对由一个或两个分离良好的障碍物填充的平面环境进行梯形分解。这个系统的优点是它是基于传感器的。
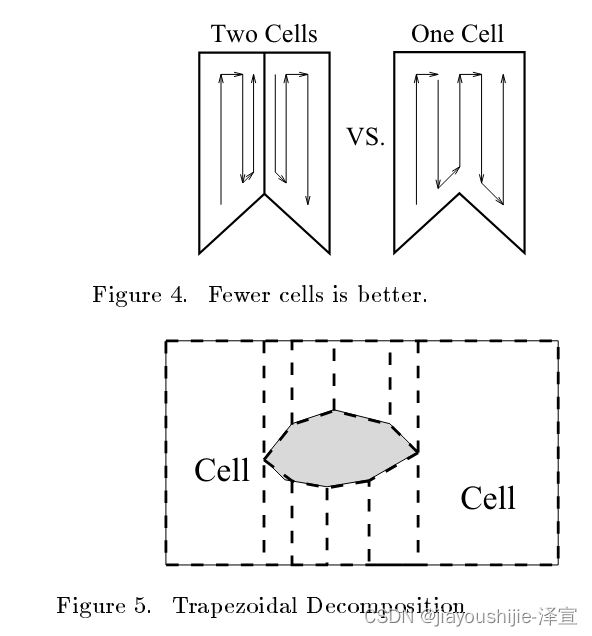
不幸的是,梯形方法需要太多冗余的来回运动来保证完备性。在图4的左侧,机器人需要进行一次额外的纵向运动来覆盖梯形单元格的剩余部分。这可以看作是保证机器人穷尽地覆盖整个环境的代价的一部分。梯形方法的另一个缺点是它要求环境是多边形的。
3 贡献
本文介绍的Boustrophedon Cell分解是对梯形分解的增强,旨在最小化前一段中描述的多余纵向运动的数量。本质上,IN和OUT事件之间的所有单元格都合并成一个单元格。比较图5中的梯形分解和图6中的Boustrophedon分解。请注意,Boustrophedon分解的单元格数量更少。
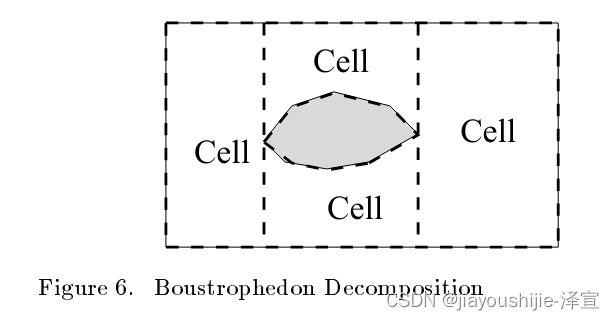
拥有更少单元格的优势在于可以最小化来回运动的boustrophedon运动的数量。例如,考虑两个相邻的梯形单元格,它们的宽度分别是机器人宽度的两倍半。为了覆盖每个梯形,机器人必须进行三次通过,总共六次纵向运动。使用Boustrophedon分解方法,这两个单元格合并成一个单调多边形单元格,需要五次通过才能覆盖(图4)。
该方法不是利用多边形的结构来确定IN和OUT事件,而是依靠切片连通性的变化来确定事件的存在。通常,这被称为关键点,关键点用于路线图运动规划技术,如Canny和Lin的"机会主义路径规划器"(OPP),它本身基于Canny的路线图算法。现在,机器人可以在曲线甚至采样环境中执行覆盖(图7)。

4 算法概述
Boustrophedon Cell分解方法与梯形分解方法相似。同样,一个切片从左到右扫过一个由多边形障碍物填充的有界平面环境。就像梯形分解一样,在IN事件中,切片连通性增加,当前单元格关闭,两个新单元格打开(图8)。相反,在OUT事件中,切片连通性减少,两个当前单元格关闭,一个新单元格打开(图9)。
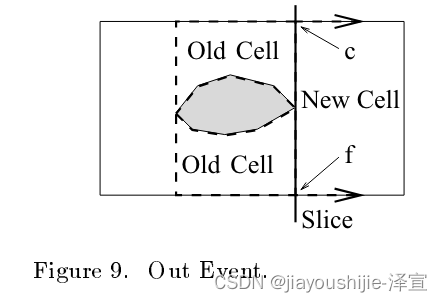
梯形分解和Boustrophedon分解方法之间的区别在于中间事件:在MIDDLE事件中,不打开也不关闭单元格,而是简单地更新当前单元格。本质上,当切片的连通性发生变化时,单元格打开和关闭(图6)。
在分解计算的同时,邻接图也被确定。同样,每个单元格是图中的一个节点,相邻单元格的节点之间有一条边。类似深度优先的图搜索算法输出一个路径列表,表示对邻接图的穷举遍历。遍历路径列表构成了对邻接图的穷举遍历。
最后,使用上述路径列表计算机器人实际走的路径。当机器人进入一个"未清洁"的单元格时,规划Boustrophedic运动,然后规划到路径列表中下一个单元格的路径。当机器人进入一个"已清洁"的单元格时,它只是规划一条穿过该单元格到路径列表中下一个单元格的路径。重复这两个动作,直到到达路径列表的末尾,即直到每个单元格都被清洁。
5 算法细节
本节包含在已知多边形环境中实现Boustrophedon分解的细节。目前的工作包括使用传感器在曲线环境中实现该算法。通过将障碍物放大机器人的半径(机器人是圆形的)来计算配置空间障碍物。由此产生的广义多边形(线段和圆弧序列)然后被多边形近似。
5.1 事件
在我们对Boustrophedon分解方法的实现中,我们用另外两种类型的事件取代了中间事件:FLOOR和CEILING。FLOOR事件对应于多边形障碍物顶部的顶点,CEILING事件对应于障碍物底部的顶点。这样,FLOOR和CEILING事件分别对应于正在逐步生成的单元格的floor和ceiling(图10)。
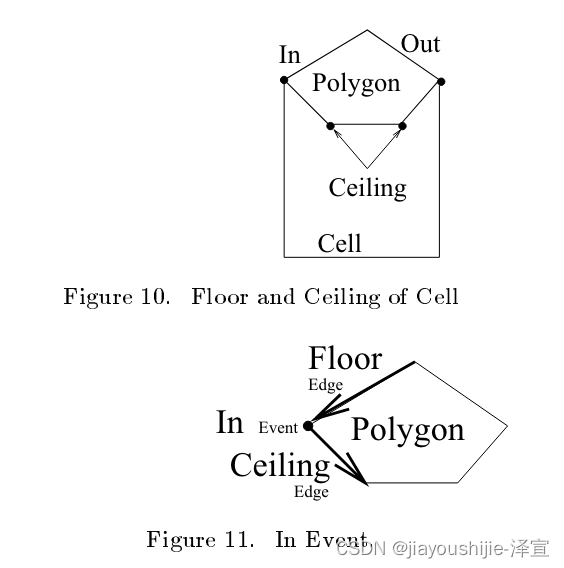
该算法的输入是一个多边形列表,其顶点按逆时针顺序列出。该算法首先从多边形列表创建一个事件列表。多边形没有特定的顺序,但在我们的实现中,我们做了一个通用假设,即没有两个IN事件或两个OUT事件具有相同的x坐标。
回想一下,事件是多边形的一个顶点和一些附加信息;具体来说,event结构包含事件的位置、类型和指向与之关联的边(或多条边)的指针。event结构最多有两种类型的边指针:floor指针和ceiling指针。IN事件的ceiling指针指向从事件发出的下一条边,floor指针指向在事件终止的前一条边(图11)。相反,OUT事件的floor指针指向从它发出的下一条边,ceiling指针指向在事件终止的边。CEILING事件只有一个ceiling指针,指向从事件发出的边;FLOOR事件只有一个floor指针,指向在事件终止的边。
在考虑特定多边形时,算法首先找到多边形的IN事件。算法遍历多边形的顶点列表,直到遇到最左边的顶点。这个顶点及其相关信息被插入到事件列表中。由于顶点是以逆时针方式排序的,下一个顶点序列是CEILING事件。回想一下,虽然这些顶点对应于多边形的下侧,但它们是CEILING事件,因为它们对应于紧接在多边形下方的单元格的ceiling。
算法遍历多边形列表,插入每个顶点作为CEILING事件,直到算法遇到最右边的顶点。这个顶点及其相关信息被插入到事件列表中作为OUT顶点。剩下的顶点对应于FLOOR事件。
当遇到事件时,将它们插入到按事件的x坐标排序的有序事件列表中。插入过程是O(n log n),其中n是多边形环境中的总边数(或顶点数)。
5.2 单元格
单元格可以用两个列表表示:一个floor边列表和一个ceiling边列表,它们都界定单元格。因此,cell结构包含两个指向边列表的指针:一个floor指针和一个ceiling指针。cell结构还包含一个指向相邻单元格的链表。最后,cell结构有两个标志:visited和cleaned,它们在算法的后面使用。
Boustrophedon分解的单元格是以增量方式通过扫描线方法计算的。扫描环境类似于按顺序访问事件列表中的每个事件,因为事件列表已经排序。
第一个单元格是最左边的单元格。在我们的实现中,假设在实际扫描过程开始之前(即,扫描从最左边的IN事件左边开始),最左边的单元格被人为地打开。还假设环境的上方由一条边界,下方由一条边界。因此,第一个单元格的floor和ceiling指针指向这些边界边。
第一个真正的事件是IN事件。在IN事件处,确定切片与当前单元格的floor的交点和切片与当前单元格的ceiling的交点。用f和c表示这些点(图8)。通常,当前单元格的floor和ceiling有多条边,因此交点f和c是当前单元格最后一条floor边和ceiling边的端点。现在,确定了当前单元格的所有floor段和ceiling段,该单元格被认为是关闭的。
接下来,要打开两个新单元格:底部单元格和顶部单元格。底部单元格的floor中第一条边的起点是点f,底部单元格的ceiling中第一条边的起点是事件。底部单元格的floor指针设置为先前关闭的单元格的floor指针,底部单元格的ceiling指针设置为打开事件的ceiling指针。相反,对于顶部单元格,floor中第一条边的起点是事件,而ceiling中第一条边的起点是点c。在这里,新的floor指针设置为事件的floor指针,新的ceiling指针设置为先前关闭的单元格的ceiling指针。
当遇到FLOOR事件时,更新当前单元格的floor指针。具体来说,与事件相关的floor边被添加到当前单元格的floor边列表中。类似地,当遇到CEILING事件时,与事件相关的ceiling边被添加到ceiling边列表中。
最后,当遇到OUT事件时,两个单元格关闭,一个新单元格打开。再次,让底部单元格和顶部单元格表示在OUT事件处关闭的两个单元格,新单元格表示在IN事件处打开的单元格。设f为当前切片与底部单元格的floor列表中当前边的交点,c为当前切片与顶部单元格的ceiling列表中当前边的交点。点f是底部单元格的floor列表中最后一段的端点,事件位置是底部单元格的ceiling列表中最后一段的端点。同样,事件位置是顶部单元格的floor列表中最后一段的端点,c是顶部单元格的ceiling列表中最后一段的端点。一旦确定了底部和顶部单元格的所有floor段和ceiling段,底部和顶部单元格就关闭了(图9)。
接下来,要打开一个新单元格。第一条floor段的起点是f,第一条ceiling段的起点是c。新单元格的floor指针设置为前一个底部单元格的floor指针,新单元格的ceiling指针设置为前一个顶部单元格的ceiling指针。
单元格邻接列表也是增量构建的。回想一下,每个单元格都有一个指向相邻单元格列表的指针,该指针在IN和OUT事件中更新。目标是将相邻单元格插入到邻接列表中,使得相邻单元格围绕当前单元格按逆时针顺序排列。在IN事件处,当前单元格被分成两个新单元格:底部和顶部。首先,顶部单元格的指针被插入到当前单元格的邻接列表的前面,然后底部单元格的指针被插入到新邻接列表的前面。结果是
neighbor_list = bottom -> top -> old_neighbor_list
在OUT事件处,底部和顶部单元格合并成一个新单元格。首先,顶部单元格的指针被插入到新单元格的邻接列表的末尾,然后底部单元格的指针被插入到邻接列表的末尾。结果是
neighbor_list = old_neighbor_list -> top -> bottom
这个过程产生了一个邻接列表,其元素是相邻单元格,从当前或新单元格的右下方开始,按逆时针方向排列。
在访问了事件列表中的所有事件后,所有单元格及其邻接关系都被计算出来;实际上,Boustrophedon分解及其邻接图已经确定。
5.3 覆盖
有了分解和邻接图,机器人现在可以规划一条覆盖环境的路径。这分两步完成:在邻接图中找到一条访问每个节点的路径,然后在每个单元格(即节点)内计算显式的机器人运动。
在通用图中确定访问每个节点的最优路径是经典的旅行商问题,这是一个NP完全问题。使用类似深度优先搜索的算法计算路径列表,路径列表表示对邻接图的穷举遍历。
- 从分解中的任意单元格开始。将其插入路径列表。将其标记为已访问。
- 转到当前单元格的邻接列表中第一个未访问的单元格(即,转到第一个逆时针未访问的单元格)。将此单元格插入路径列表的开头,并将其标记为已访问。
- 重复此过程(即,转到步骤2),直到遇到所有邻居都已访问的单元格。
- 在这一点上,回溯,直到遇到具有未访问邻居的单元格。通过向前遍历路径列表来实现此回溯,将访问的每个元素插入路径列表的前面,直到遇到具有未访问邻居的元素。将此元素插入路径列表的前面,然后重复上述过程(即,转到步骤2)。
- 如果在回溯过程中没有找到具有未访问邻居的单元格,则邻接图中的所有单元格都已被访问。
使用路径列表,机器人的运动是通过两步过程计算的。首先,如果单元格未被清洁,则将该单元格标记为已清洁,并为该单元格计算实际的Boustrophedon(来回)运动。通常,Boustrophedon运动的步长(即两条平行线段之间的距离)大约是机器人的宽度。其次,确定到路径列表中下一个单元格的路径。如果单元格已经被清洁,则规划到路径列表中下一个单元格的路径。
6 仿真和实验
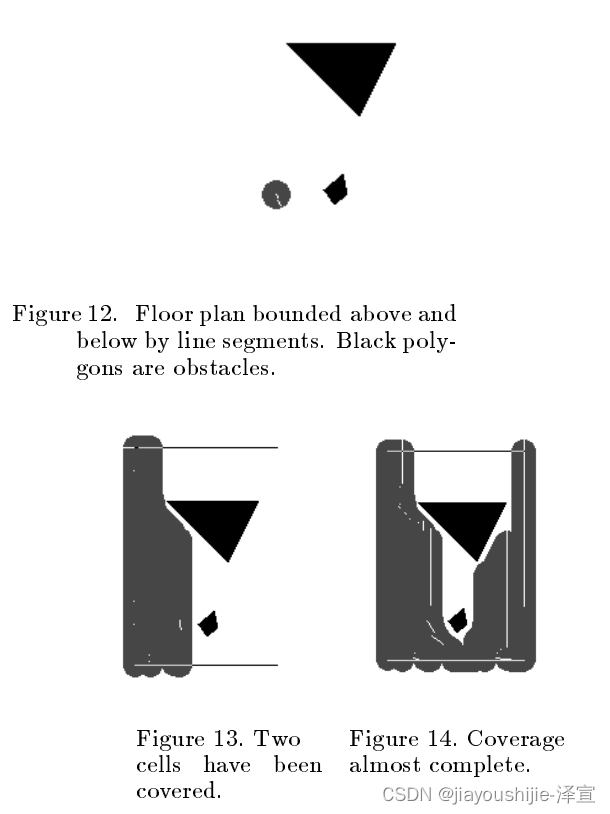
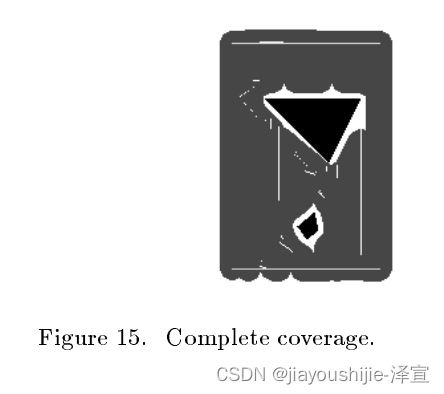
图12包含两个障碍物的地板平面图。图13和14包含地板覆盖算法的中间结果。在图13中,两个单元格已经被覆盖,在图14中,除两个单元格外,所有单元格都被覆盖。最终的覆盖结果可以在图15中看到。
从图15可以看出,这种方法在障碍物边缘与Boustrophedon来回路径形成锐角时存在一些问题。为了部分缓解这个问题,当机器人穿过已清洁的单元格时,它靠近障碍物的边界行进。未来的实现将包括一个额外的通道,其中每个障碍物都被特别环绕。对于真空吸尘等应用,这种额外的方法是合理的,因为大多数真空吸尘应用在环境边界附近需要不同的吸尘机制。
该算法还在铺有地毯的环境中的Nomadic Technologies移动机器人基座上运行,环境中有纸板障碍物,由上述仿真表示。该实现在小环境中有效,但在较大的环境中存在一些航位推算问题。特别是,并非所有线条都完全平行。这种方法可以从Demeter项目中使用的基于视觉的技术中受益。此外,我们的实验表明,这种方法对初始条件极其敏感,因此未来的工作必须使这个过程对初始条件的微小变化具有鲁棒性。
7 结论和未来工作
本文描述了一种新型的地板覆盖算法,该算法是完备的。也就是说,从理论上讲,机器人保证遵循一条路径,使得机器人经过环境中的每个点。该算法基于一种称为Boustrophedon Cell分解的新型精确Cell分解方法。Boustrophedon的意思是"牛的方式";Boustrophedon运动是来回牛样的运动。机器人可以很容易地在Boustrophedon分解的每个单元格中规划Boustrophedon运动。一旦每个单元格被覆盖,整个环境就被覆盖了。
移动机器人上的实验结果验证了这种方法,并指出了未来工作的一些途径。由于侧向步长的离散化,这种方法有时会跳过障碍物边界附近的环境部分。如果机器人的侧向步长较短,则这些未覆盖的区域会减少。这里有一个时间/覆盖的权衡。尽管如此,在主要覆盖完成后,一个简单的障碍物跟随算法将缓解这个问题。这样的解决方案与正常的真空吸尘一致,其中地板靠近墙壁的部分需要用真空吸尘器额外通过一遍。
近期研究还包括通过允许定义更大(因此更少)的单元格来改进Boustrophedon Cell分解。例如,在图6中,底部的三个单元格可以合并成一个单元格,其中可以规划Boustrophedon运动。此外,由于单元格在扫描线的连通性发生变化时打开或关闭,因此该算法可以很容易地修改为具有曲线障碍物的环境。
此外,还需要考虑优化问题。第一个问题涉及开发度量标准,用于评估邻接图的启发式图搜索。这些度量包括:路径长度、重新覆盖的地板空间面积、时间等。另一个优化问题涉及确定扫描线的角度;某些环境可能更适合水平扫描线。
另一个问题涉及材料去除。在真空吸尘器的情况下,这一点并不重要。然而,在除雪的情况下,除雪机器人可能必须规划最佳路径,将雪转移到覆盖现场。这暗示了使用多个机器人:一个机器人从地面上清除雪,另一个机器人将雪转移到中央倾倒区。
这项工作的长期目标是基于传感器的地板覆盖,即仅从视线传感器信息确定覆盖路径。即使机器人可以获得世界的全部知识,基于传感器的地板覆盖也是有用的,但输入机器人太麻烦了。例如,如果每个用户都必须将房屋CAD模型(如果存在)编程到机器人中,自动真空吸尘器就不会成为一个有市场的产品。基于传感器的方法将基于Rimon和Canny的路线图工作,该工作使用关键点来保证路线图的连通性。
Code
import numpy as np
import matplotlib.pyplot as plt
from typing import List, Tuple
from matplotlib.patches import RegularPolygon
Point = Tuple[int, int]
Cell = List[Point]
def is_adjacent(cell1: Cell, cell2: Cell) -> bool:
"""
判断两个单元格是否相邻
"""
for p1 in cell1:
for p2 in cell2:
if abs(p1[0] - p2[0]) + abs(p1[1] - p2[1]) == 1:
return True
return False
def merge_cells(cells: List[Cell]) -> List[Cell]:
"""
合并相邻的单元格
"""
merged_cells = []
for cell in cells:
merged = False
for i, merged_cell in enumerate(merged_cells):
if is_adjacent(cell, merged_cell):
merged_cells[i] = merged_cell + cell
merged = True
break
if not merged:
merged_cells.append(cell)
return merged_cells
def bcd(env: np.ndarray) -> np.ndarray:
"""
Boustrophedon Cellular Decomposition
"""
rows, cols = env.shape
cell_grid = np.zeros_like(env, dtype=int) # 创建一个与环境大小相同的网格,用于存储单元格的ID
cell_id = 1 # 初始单元格ID为1
for col in range(cols):
slice = env[:, col] # 获取当前列的数据
cells = [] # 存储当前列的单元格
cell = [] # 存储当前单元格的像素坐标
for row in range(rows):
if slice[row] == 0: # 如果当前像素是障碍物
if cell: # 如果当前单元格非空
cells.append(cell) # 将当前单元格添加到cells列表中
cell = [] # 重置当前单元格为空
else: # 如果当前像素是自由空间
cell.append((row, col)) # 将当前像素的坐标添加到当前单元格中
if cell: # 如果最后一个单元格非空
cells.append(cell) # 将最后一个单元格添加到cells列表中
if col == 0: # 如果是第一列
for cell in cells: # 遍历第一列的每个单元格
for row, col in cell: # 遍历单元格中的每个像素坐标
cell_grid[row, col] = cell_id # 将像素点标记为当前单元格的ID
cell_id += 1 # 单元格ID加1
else: # 如果不是第一列
prev_cells = [] # 存储上一列的单元格信息
for row in range(rows):
if cell_grid[row, col-1] != 0: # 如果上一列的当前行不是障碍物
prev_cell = [(row, col-1)] # 初始化一个新的上一列单元格
while col > 0 and cell_grid[row, col-1] == cell_grid[row, col-2]: # 向左遍历,找到连续的、属于同一单元格的像素
prev_cell.append((row, col-2)) # 将像素坐标添加到当前的上一列单元格中
col -= 1 # 列号减1,继续向左遍历
prev_cells.append(prev_cell) # 将当前的上一列单元格添加到prev_cells列表中
i = 0 # 上一列单元格的索引
for cell in cells: # 遍历当前列的每个单元格
if i < len(prev_cells) and len(cell) == len(prev_cells[i]): # 如果当前单元格与上一列的对应单元格长度相同
for row, col in cell: # 遍历当前单元格的每个像素坐标
cell_grid[row, col] = cell_grid[prev_cells[i][0]] # 将像素点标记为上一列对应单元格的ID
i += 1 # 上一列单元格索引加1
else: # 如果当前单元格与上一列的对应单元格长度不同,或者上一列没有对应单元格
for row, col in cell: # 遍历当前单元格的每个像素坐标
cell_grid[row, col] = cell_id # 将像素点标记为新的单元格ID
cell_id += 1 # 单元格ID加1
return cell_grid # 返回生成的单元格网格
def merge_cells_bcd(cell_grid: np.ndarray, threshold: int = 5) -> np.ndarray:
"""
合并BCD算法生成的单元格
:param cell_grid: 单元格网格
:param threshold: 长度差阈值,默认为5
:return: 合并后的单元格网格
"""
rows, cols = cell_grid.shape
merged_grid = np.copy(cell_grid) # 创建一个副本,用于存储合并后的单元格网格
for col in range(1, cols): # 从第二列开始遍历
prev_cell_id = None # 上一个单元格的ID
prev_cell_length = 0 # 上一个单元格的长度
for row in range(rows):
curr_cell_id = cell_grid[row, col] # 当前单元格的ID
if curr_cell_id != 0: # 如果当前单元格不是障碍物
if curr_cell_id == prev_cell_id: # 如果当前单元格与上一个单元格ID相同
curr_cell_length = prev_cell_length + 1 # 当前单元格长度加1
else: # 如果当前单元格与上一个单元格ID不同
curr_cell_length = 1 # 重置当前单元格长度为1
if prev_cell_id is not None and curr_cell_id != prev_cell_id: # 如果上一个单元格存在,且与当前单元格ID不同
if abs(prev_cell_length - curr_cell_length) < threshold: # 如果上一个单元格长度与当前单元格长度差小于阈值
merged_grid[row - prev_cell_length : row, col] = prev_cell_id # 将当前单元格合并到上一个单元格
else: # 如果长度差大于等于阈值
prev_cell_id = curr_cell_id # 更新上一个单元格ID为当前单元格ID
prev_cell_length = curr_cell_length # 更新上一个单元格长度为当前单元格长度
else: # 如果上一个单元格不存在,或者与当前单元格ID相同
prev_cell_id = curr_cell_id # 更新上一个单元格ID为当前单元格ID
prev_cell_length = curr_cell_length # 更新上一个单元格长度为当前单元格长度
return merged_grid
def generate_environment(shape=(600, 1200), n_stars=15, n_triangles=15, max_size=50):
"""
随机生成一个环境
:param shape: 环境的形状(高度,宽度)
:param n_stars: 五角星的数量
:param n_triangles: 三角形的数量
:param max_size: 图形的最大尺寸
:return: 生成的环境图像
"""
env = np.ones(shape, dtype=np.uint8)
# 随机生成五角星
for _ in range(n_stars):
x, y = np.random.randint(0, shape[1]), np.random.randint(0, shape[0])
size = np.random.randint(10, max_size)
star = RegularPolygon((x, y), 5, radius=size, orientation=np.random.uniform(0, 2*np.pi), facecolor='black')
plt.gca().add_patch(star)
# 随机生成三角形
for _ in range(n_triangles):
x, y = np.random.randint(0, shape[1]), np.random.randint(0, shape[0])
size = np.random.randint(10, max_size)
triangle = RegularPolygon((x, y), 3, radius=size, orientation=np.random.uniform(0, 2*np.pi), facecolor='black')
plt.gca().add_patch(triangle)
plt.axis('equal')
plt.axis('off')
plt.tight_layout()
fig = plt.gcf()
fig.canvas.draw()
env = np.array(fig.canvas.renderer._renderer)[:, :, 0]
env = 1 - (env < 128).astype(np.uint8)
plt.close()
return env
def display_grid(env: np.ndarray, cell_grid: np.ndarray):
"""
显示原始环境和分解后的单元格网格
"""
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 6))
ax1.imshow(env, cmap='binary')
ax1.set_title('Original Environment')
ax1.axis('off')
cell_colors = np.random.rand(np.max(cell_grid) + 1, 3)
cell_colors[0] = [1, 1, 1] # 障碍物为白色
ax2.imshow(cell_colors[cell_grid])
ax2.set_title('BCD Grid')
ax2.axis('off')
plt.tight_layout()
plt.show()
# 测试代码
env = generate_environment(shape=(600, 1200), n_stars=30, n_triangles=30, max_size=80)
cell_grid = bcd(env)
display_grid(env, cell_grid) # 显示合并后的单元格网格