前言
在讲堆的删除时,我们发现一步一步删除堆顶的数据,排列起来呈现出排序的规律,所以本节小编将带领大家进一步理解堆排序。
1.堆排序概念
那么什么是堆排序?
堆排序(Heap Sort)是一种基于堆数据结构的排序算法。它利用堆的性质(大堆或小堆)进行排序操作。堆排序的基本思想是通过构建堆,将待排序的数组转化为一个符合堆性质的堆结构,然后不断将堆顶元素与堆的最后一个元素进行交换,并调整堆,使剩余元素继续满足堆的性质。重复这个过程,直到整个数组有序。
堆排序的步骤如下:
- 构建大堆或小堆:将待排序的数组视为一个完全二叉树,通过从最后一个非叶子节点开始,依次对每个节点进行向下调整(Adjustdown)操作,构建出一个大堆或小堆。这个过程确保了堆的性质:对于大堆,父节点的值大于等于其子节点的值;对于小堆,父节点的值小于等于其子节点的值。
- 排序 :交换堆顶元素(最大值或最小值)与堆的最后一个元素,并将堆的大小减一。然后对堆顶元素进行向下调整,使剩余元素继续满足堆的性质。重复这个过程,直到堆的大小为1,即所有元素都已经排好序。(运用堆删除的思想)
- 得到排序结果:经过上述步骤,数组中的元素就按照升序(从小到大)或降序(从大到小)排列了。
堆排序的时间复杂度为 O(nlogn),其中 n 是待排序数组的大小。它具有原地排序的特点,不需要额外的存储空间。
堆排序的优点是稳定性较好,适用于大规模数据的排序。然而,堆排序的缺点是相对较慢,尤其在快速排序等其他排序算法的应用场景中,堆排序的性能可能不如其他算法。
2.堆的建立方法
2.1向下调整建立堆(补充)
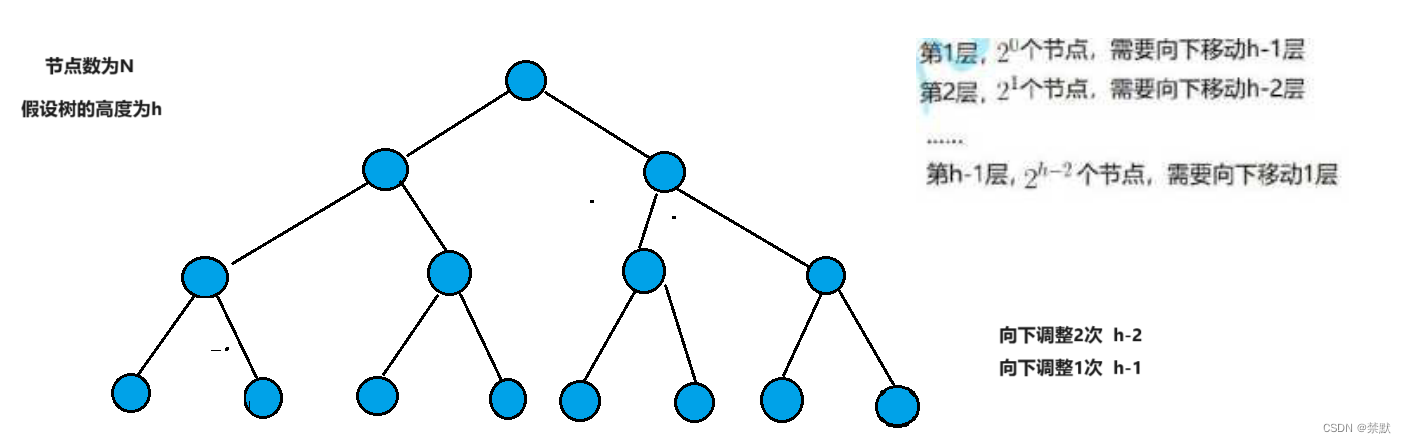
在这里,堆的建立有两种,在二叉树的顺序结构中提到一种建堆的方法,通过尾插再进行向上调整,不过时间复杂度为O(N*logN),这里提供新的建堆方法,通过向下调整法,时间复杂度为O(N),不过再用此调整方法时,左右子树要是堆的结构。即**从倒数的第一个非叶子结点的子树开始调整,一直调整到根结点的树,**就可以调整成堆。
假设给一个数组 int a[]={4,2,8,1,5,6,9,7,2,7,9},通过向下调整法制造大堆。

2.2向上调整法
通过比较新插入元素与其父节点的值来判断是否需要进行交换。如果新插入元素的值大于父节点的值,就将它们进行交换,并更新索引值。这样,逐步向上调整,直到新插入元素找到了合适的位置,保证了堆的性质。
cs
//向上调整
void Adjustup(Datatype* a,int child) {
int parent = (child - 1) / 2;
while (child > 0) {
if (a[child] > a[parent]) {
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
break;
}
}2.3建堆时间复杂度分析
1.向下调整法
cs
void Adjustdown(Datatype* a, int n, int parent) {
//假设法,假设左孩子大
int child = parent * 2 + 1;
while (child < n ) {
if (child + 1 < n && a[child + 1] > a[child])
child = child + 1;
if (a[child] > a[parent]) {
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else break;
}
}

2.向上调整法
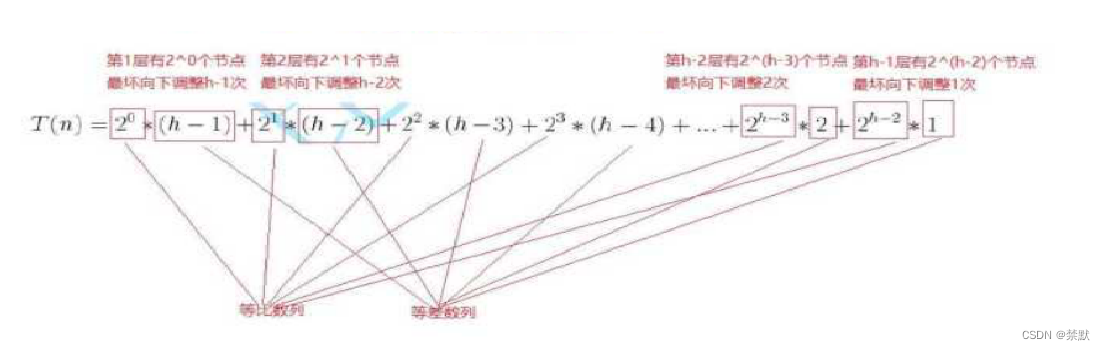
向上调整法每层节点向上调整次数就是乘以层数

cs
//向上调整
void Adjustup(Datatype* a,int child) {
int parent = (child - 1) / 2;
while (child > 0) {
if (a[child] > a[parent]) {
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
break;
}
}注意:上述代码都是采用建大堆的代码,建小堆把部分大于符号改成小于。
因此向下调整法实质上是节点数少的层,调整次数越多,向上调整是节点数越多,调整次数越多。
3.排序建堆选择
升序:建大堆
降序:建小堆
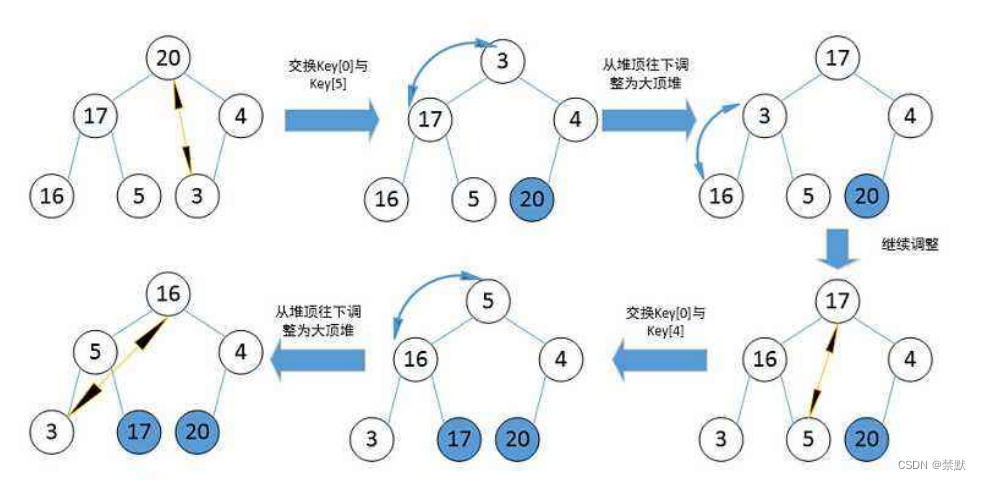
每次将堆首元素与尾元素交换,然后向下调整,每交换一次,堆的大小要减一,因为我们是每次将最大或者最小的元素依次交换堆后面。
例如升序的一个过程如下图:

cs
void HeapSort(int* a, int n)
{
//降序,建小堆
// 升序,建大堆
//for (int i = 1; i < n; i++)
//{
// Adjustup(a, i);
//}
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
Adjustdown(a, n, i);
}
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
Adjustdown(a, end, 0);
--end;
}
}
void TestHeap2()
{
int a[] = {20,17,16,5,3,4 };
HeapSort(a, sizeof(a) / sizeof(int));
for (int i = 0; i < sizeof(a) / sizeof(int); i++) {
printf("%d ", a[i]);
}
}4.TOP-K****问题
TOP-K 问题:即求数据结合中前 K 个最大的元素或者最小的元素,一般情况下数据量都比较大 。
比如:专业前 10 名、世界 500 强、富豪榜、游戏中前 100 的活跃玩家等。
对于 Top-K 问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了 ( 可能数据都不能一下子全部加载到内存中) 。最佳的方式就是用堆来解决,基本思路如下:
若数据量小,可以直接建立相应的堆,在pop。
数据量很大的时候,可以采用以下方法:
- 用数据集合中前 K 个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆
- 用剩余的 N-K 个元素依次与堆顶元素来比较,不满足则替换堆顶元素
将剩余 N-K 个元素依次与堆顶元素比完之后,堆中剩余的 K 个元素就是所求的前 K 个最小或者最大的元素。
假如求一堆数中的前k个最小的数,则建大堆。
这里我们采用随机数来生成100个随机数,然后存入一个动态数组中,然后选出前10个最小的数。
cs
void PrintTopK(int* a, int n, int k)
{
// 1. 建堆--用a中前k个元素建堆
for (int i = (k - 1 - 1) / 2; i >= 0; i--) {
Adjustdown(a, k, i);
}
// 2. 将剩余n-k个元素依次与堆顶元素交换,不满则则替换
for (int j = n - k; j < n; j++) {
if (a[j] < a[0]) {
a[0] = a[j];
Adjustdown(a, k, 0);
}
}
printf("最小前%d个数:", k);
for (int i = 0; i < k; i++) {
printf("%d ", a[i]);
}
}
void TestTopk()
{
int n = 100;
int* a = (int*)malloc(sizeof(int) * n);
srand(time(0));
for (size_t i = 0; i < n; ++i)
{
a[i] = rand() % 100;
}
PrintTopK(a, n, 10);
}本节内容到此结束,谢谢各位友友的捧场,下节小编将带领大家继续了解二叉树的链式存储结构!!!
留下三连和评论吧!!!