文章目录
- 属性
- [二叉树Binary Tree](#二叉树Binary Tree)
- 应用
- 二叉树
具有层级结构
一对多
Node结点
root根
Children孩子
Parent双亲
Sibling兄弟 有同一个双亲
leaf 叶子 没有孩子
结点的层次(level):从根结点算起,根为第一层,它的孩子为第二层......
结点的度(degree):结点拥有的子树数
树的度:一棵树中最大的结点度数
属性
可以递归定义,调用自己,孩子又是一棵树的根节点。
有n个结点node,那么有n-1个边edge
深度 Depth 从根到x的edge的数目,根的Depth为0,国内根的深度为1
高度Height 从x到叶子结点的最多 边的数目,国内高度要加1
树的高度是根结点的高度
结点的度(degree):结点拥有的子树数
二叉树Binary Tree
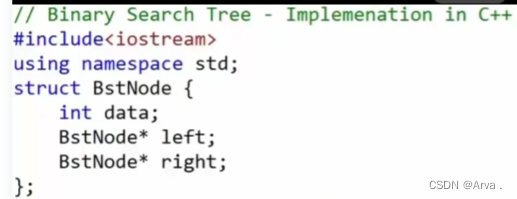
最常见的实现,结点三个域,左孩子,右孩子,数据域。
应用
存储天然具备层级结构的数据
文件和文件夹
组织数据
让集合快速查找 删除等
Tire树 动态的拼写检查
network Routing algorithm网络路由算法
二叉树
一个最多有两个孩子
严格二叉树
每个结点有0或两个孩子
完全二叉树
除了最后一层都填满,并且最后一层的结点若没有完全填充,那么向左对齐
满二叉树Perfect Binary Tree
最后一层也满,所有的都满,是完全二叉树的特例
二叉搜索树Binary Search Tree
用数目数据结构来存储可修改的集合
这样要求快速查找,插入,删除
array
end标记结尾,
search 从开头到结尾,故O(n)
insert 若插入末尾 O(1),若满,O(n)
remove O(n)
Linked LIst
搜索O(n)
头部插入O(1)
删除O(n)
Array(sortrd)
查找的话,O(n)时间复杂度太大。如果排序了
的话,可以使用二分查找。所以在插入和删除的时候,我们就要对这个数组排好序。排序后的数组查找很方便,但是插入和删除依旧要O(n)

Binary Search Tree(balanced)
a balanced tree (对于任何结点,左右子树的高度差不大于1)
对于每一个结点,所有 (故下图16大于15,不是BST)左子树的结点值都比该结点上的值小或等于,右子树上的结点值比该节点的值大
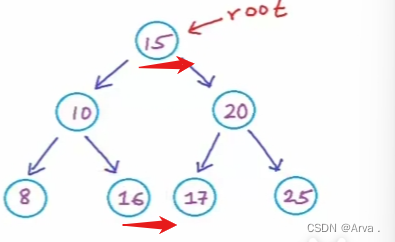

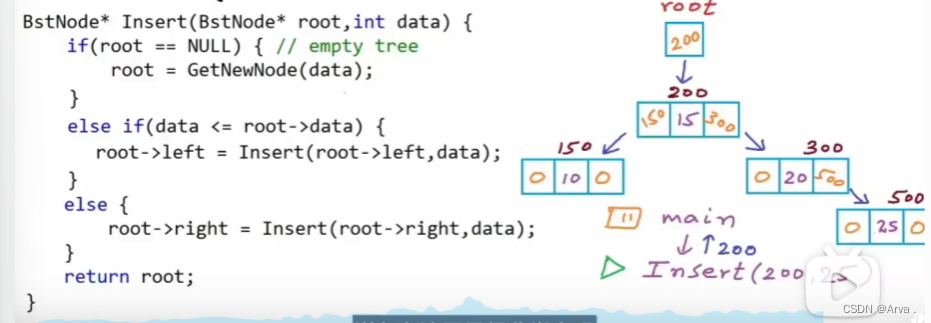
递归构建二叉树
判断该数字在二叉树中是否存在

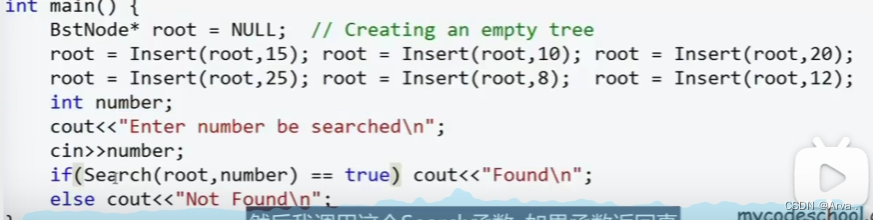
笔者认为这里的插入函数仅仅能满足每个结点的左节点小于等于该结点,右节点大于该节点。而不能满足二叉搜索树中的所有要求
性质
在非空二叉树中,第i层上至多有2i-1个结点(i≧1)
性质2:深度为k的二叉树至多有2k-1个结点(k≧1)( 2 0+21+ ...+2k-1=2k-1 )
对任何一棵二叉树,若其叶子结点数为n0,度为2的结点数为n2,则n0=n2+1
n个结点的完全二叉树深度为:㏒以二为底n向下取整+1。
实现
dynamically
最常见的实现,结点三个域,左孩子,右孩子,数据域。
arrays数组
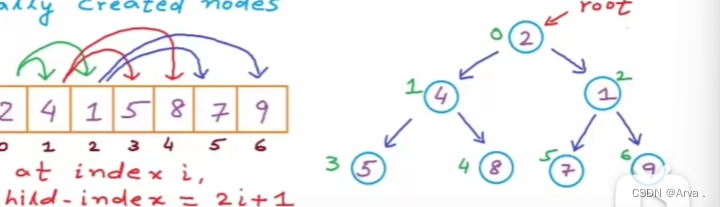
对于完全二叉树上编号为i的结点元素存储在一维数组的下标值为i-1的分量中。
对于一般的二叉树,将其每个结点与完全二叉树上的结点相对照,存储在一维数组中。数组下标为i,对应二叉树结点的标号为i+1(国内,国外对应的还是i),那么左孩子的索引是2i+1,右孩子的索引是2 i+2,辅助记忆(记忆根和左右结点的关系
国外版