例题一

解法(贪⼼):
贪⼼策略:
⽤尽可能多的字符去构造回⽂串:
a. 如果字符出现偶数个,那么全部都可以⽤来构造回⽂串;
b. 如果字符出现奇数个,减去⼀个之后,剩下的字符能够全部⽤来构造回⽂串;
c. 最后再判断⼀下,如果有字符出现奇数个,就把它单独拿出来放在中间。

例题二

解法(贪⼼):
贪⼼策略:
a. 当遇到 'I' 的时候,为了让下⼀个上升的数可选择的「范围更多」,当前选择「最⼩」的那个数;
b. 当遇到 'D' 的时候,为了让下⼀个下降的数可选择的「范围更多」,选择当前「最⼤」的那个数。

例题三

贪⼼策略:
先将两个数组排序。
针对胃⼝较⼩的孩⼦,从⼩到⼤挑选饼⼲:
i. 如果当前饼⼲能满⾜,直接喂(最⼩的饼⼲都能满⾜,不要浪费⼤饼⼲);
ii. 如果当前饼⼲不能满⾜,放弃这个饼⼲,去检测下⼀个饼⼲(这个饼⼲连最⼩胃⼝的孩⼦都⽆法满⾜,更别提那些胃⼝⼤的孩⼦了)。

例题四
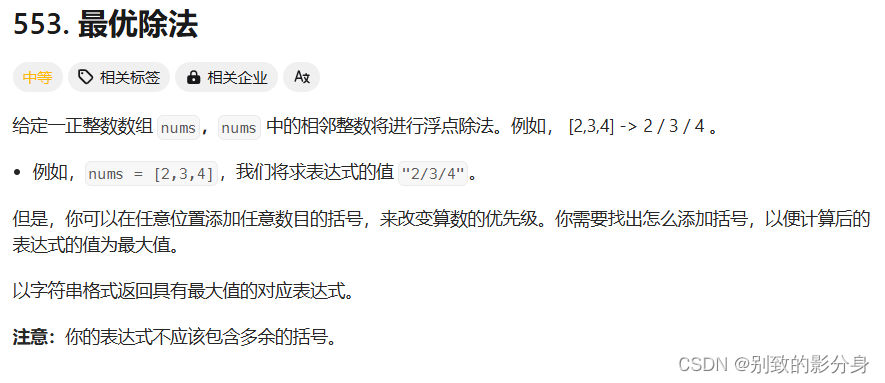
解法(贪⼼):
贪⼼策略:
在最终的结果中,前两个数的位置是⽆法改变的。因为每⼀个数的都是⼤于等于 2 的,为了让结果更⼤,我们应该尽可能的把剩下的数全都放在「分⼦」上.

例题五

解法(动态规划 + 类似层序遍历):
动态规划:
a. 状态表⽰:
dp[i] 表⽰从 0 位置开始,到达 i 位置时候的最⼩跳跃次数。
b. 状态转移⽅程:
对于 dp[i] ,我们遍历 0 ~ i - 1 区间(⽤指针 j 表⽰),只要能够从 j 位置跳到 i 位置( nums[j] + j >= i ),我们就⽤ dp[j] + 1 更新 dp[i] ⾥⾯的值,找到所有情况下的最⼩值即可。
类似层序遍历的过程:
⽤类似层序遍历的过程,将第 i 次跳跃的「起始位置」和「结束位置」找出来,⽤这次跳跃的情
况,更新出下⼀次跳跃的「起始位置」和「终⽌位置」。这样「循环往复」,就能更新出到达 n - 1 位置的最⼩跳跃步数。

例题六

解法:
和 跳跃游戏II ⼀样,仅需修改⼀下返回值即可。
