4.3 差错检测与纠正:海明距离与海明码**
在计算机网络的数据传输过程中,物理信道往往不是理想的。由于热噪声、电磁干扰等因素的影响,数据在传输过程中可能会发生比特翻转(例如,发送的 '0' 变成了 '1')。为了保证数据通信的可靠性,必须引入差错控制机制。本节将深入探讨一种经典的纠错编码理论基础------海明距离(Hamming Distance),以及基于此理论构建的海明码(Hamming Code)。
4.3.1 差错控制的基础:海明距离
在理解如何"纠正"错误之前,我们首先需要量化"错误"。1950年,理查德·海明(Richard Hamming)提出了海明距离的概念,为差错控制理论奠定了基石。
1. 定义
两个等长二进制码字(Code Word)之间,对应位上数值不同的位数,称为这两个码字之间的海明距离。
通俗地说,海明距离就是把一个码字变成另一个码字,所需要改变的最小比特数。我们通常用 d(x,y)d(x, y)d(x,y) 表示码字 xxx 和 yyy 之间的海明距离。可以通过对两个码字进行**异或(XOR)**运算,然后统计结果中 '1' 的个数来计算。
示例:
假设有两个码字:
x=10101y=10001 \begin{aligned} x &= 10101 \\ y &= 10001 \end{aligned} xy=10101=10001
进行异或运算:10101⊕10001=0010010101 \oplus 10001 = 0010010101⊕10001=00100。结果中包含 1 个 '1',因此 d(x,y)=1d(x, y) = 1d(x,y)=1。这意味着这两个码字之间只有 1 位不同。
2. 最小海明距离与编码能力
对于一个编码系统(包含所有合法的码字集合),该系统中任意两个合法码字之间海明距离的最小值,称为该编码系统的最小海明距离 ,记为 dmind_{min}dmin。
dmind_{min}dmin 直接决定了该编码系统的检错和纠错能力:
-
检错能力 :
为了检测出 eee 个比特的错误,要求编码系统的最小海明距离满足:
dmin≥e+1 d_{min} \geq e + 1 dmin≥e+1
原理解析:如果合法码字之间的距离只有 1,那么传输中发生 1 位跳变,就会变成另一个合法的码字,接收方无法察觉。只有当距离拉大,错误发生后的码字才会落入"非法码字"区域,从而被检测出来。 -
纠错能力 :
为了纠正 ttt 个比特的错误,要求编码系统的最小海明距离满足:
dmin≥2t+1 d_{min} \geq 2t + 1 dmin≥2t+1
原理解析 :这可以理解为几何上的"势力范围"。如果两个合法码字 AAA 和 BBB 距离足够远(例如距离为 3),那么 AAA 发生 1 位错误变成 A′A'A′,A′A'A′ 距离 AAA 的距离为 1,距离 BBB 的距离为 2。接收方根据"择近原则",会判定 A′A'A′ 大概率是由 AAA 产生的,从而将其纠正回 AAA。

4.3.2 海明码的设计原理
海明码是一种利用奇偶校验位的纠错码,它不仅能检测错误,还能指出错误发生的位置,从而实现自动纠正。最常用的是能够纠正 1 位错误的海明码。
1. 冗余位的计算
假设我们要发送的数据长度为 mmm 位,为了能够纠正 1 位错误,我们需要添加 rrr 位冗余校验位(Check Bits),使得编码后的总长度为 n=m+rn = m + rn=m+r。
这 rrr 个校验位需要能够指示出 m+rm + rm+r 个位置中哪一位出错了,或者指示没有错误。因此,校验位所能表示的状态总数 2r2^r2r 必须覆盖所有可能的情况:
2r≥m+r+1 2^r \geq m + r + 1 2r≥m+r+1
其中:
- m+rm + rm+r 代表错误可能发生在任意一位数据位或校验位上。
- +1+ 1+1 代表"没有错误"这种状态。
常见配置:
- 若数据位 m=4m=4m=4,代入公式:2r≥4+r+12^r \geq 4 + r + 12r≥4+r+1。当 r=3r=3r=3 时,8≥88 \geq 88≥8 成立。这就是经典的 (7, 4) 海明码(总长7位,数据4位)。
2. 校验位的布局
海明码巧妙地将校验位安插在 2 的幂次位置上(即第 1, 2, 4, 8, ... 位),其余位置填入数据位。
以 (7, 4) 海明码为例,位号从左到右为 1 到 7:
- 校验位 PiP_iPi :位于第 1,2,41, 2, 41,2,4 位。
- 数据位 DjD_jDj :位于第 3,5,6,73, 5, 6, 73,5,6,7 位。
| 位号 (Index) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 内容 | P1P_1P1 | P2P_2P2 | D1D_1D1 | P4P_4P4 | D2D_2D2 | D3D_3D3 | D4D_4D4 |
3. 校验规则(核心算法)
每个校验位 PiP_iPi 负责校验一组特定的位置。判断某一位 kkk 是否由校验位 PiP_iPi 负责,只需看 kkk 的二进制表示中,第 iii 位是否为 1。
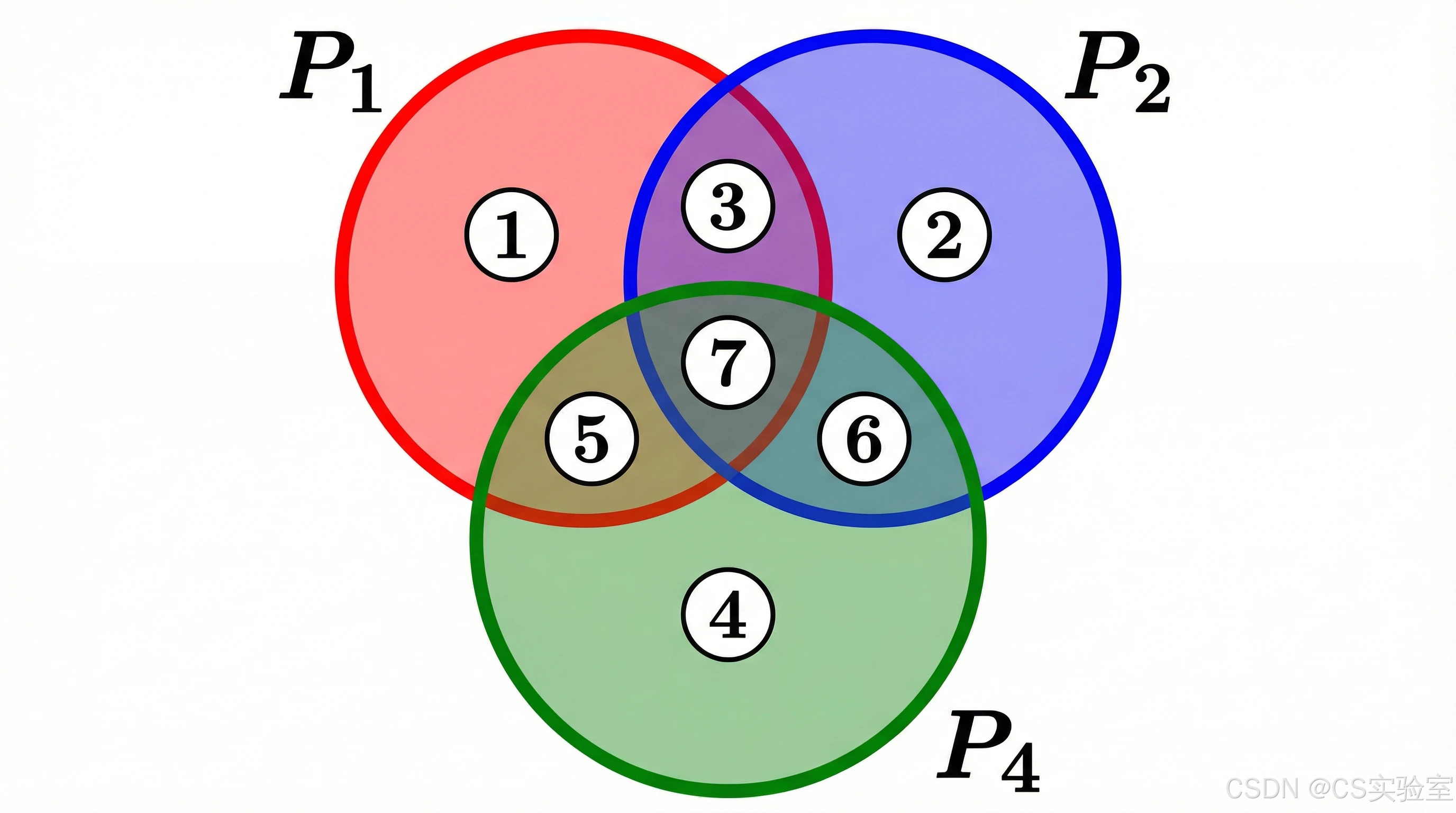
- P1P_1P1 (二进制权重 1) :负责校验位号二进制末位为 1 的位置。
即:1 (001), 3 (011), 5 (101), 7 (111)。 - P2P_2P2 (二进制权重 2) :负责校验位号二进制倒数第二位为 1 的位置。
即:2 (010), 3 (011), 6 (110), 7 (111)。 - P4P_4P4 (二进制权重 4) :负责校验位号二进制倒数第三位为 1 的位置。
即:4 (100), 5 (101), 6 (110), 7 (111)。
通常采用偶校验,即让负责组内的所有位(包括校验位自己)的 '1' 的个数为偶数。
4.3.3 海明码编码与纠错实例
1. 编码过程
假设要传输的数据为 101110111011(即 D1=1,D2=0,D3=1,D4=1D_1=1, D_2=0, D_3=1, D_4=1D1=1,D2=0,D3=1,D4=1)。
步骤 1:填入数据
| 位号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 值 | P1P_1P1 | P2P_2P2 | 1 | P4P_4P4 | 0 | 1 | 1 |
步骤 2:计算校验位(偶校验)
- 计算 P1P_1P1 :涉及位置 1, 3, 5, 7。现有值:?,1,0,1?, 1, 0, 1?,1,0,1。
1⊕0⊕1=01 \oplus 0 \oplus 1 = 01⊕0⊕1=0(已有偶数个1)。为了保持总数为偶数,P1=0P_1 = 0P1=0。 - 计算 P2P_2P2 :涉及位置 2, 3, 6, 7。现有值:?,1,1,1?, 1, 1, 1?,1,1,1。
1⊕1⊕1=11 \oplus 1 \oplus 1 = 11⊕1⊕1=1(已有奇数个1)。为了凑成偶数,P2=1P_2 = 1P2=1。 - 计算 P4P_4P4 :涉及位置 4, 5, 6, 7。现有值:?,0,1,1?, 0, 1, 1?,0,1,1。
0⊕1⊕1=00 \oplus 1 \oplus 1 = 00⊕1⊕1=0(已有偶数个1)。为了保持总数为偶数,P4=0P_4 = 0P4=0。
最终发送的码字 :011001101100110110011。
2. 纠错过程
假设在传输过程中,第 3 位发生了翻转,接收到的数据变成了 010001101\mathbf{0}00110100011(原为 1,现为 0)。
接收方重新计算三个校验组的奇偶性(称为指错字 或伴随式 ,Syndrome),记为 S4S2S1S_4 S_2 S_1S4S2S1:
- 检查 S1S_1S1 (组 1,3,5,7) :接收到的值为 0,0,0,10, 0, 0, 10,0,0,1。
0⊕0⊕0⊕1=10 \oplus 0 \oplus 0 \oplus 1 = 10⊕0⊕0⊕1=1 (奇数,出错)。S1=1S_1 = 1S1=1。 - 检查 S2S_2S2 (组 2,3,6,7) :接收到的值为 1,0,1,11, 0, 1, 11,0,1,1。
1⊕0⊕1⊕1=11 \oplus 0 \oplus 1 \oplus 1 = 11⊕0⊕1⊕1=1 (奇数,出错)。S2=1S_2 = 1S2=1。 - 检查 S4S_4S4 (组 4,5,6,7) :接收到的值为 0,0,1,10, 0, 1, 10,0,1,1。
0⊕0⊕1⊕1=00 \oplus 0 \oplus 1 \oplus 1 = 00⊕0⊕1⊕1=0 (偶数,正常)。S4=0S_4 = 0S4=0。
定位错误:
将指错字 S4S2S1S_4 S_2 S_1S4S2S1 也就是 011011011 转换为十进制:
(011)2=3 (011)_2 = 3 (011)2=3
结果直指第 3 位 出错!接收方只需将第 3 位的数据取反(0 改回 1),即可恢复原始数据。如果所有 SSS 均为 0,则说明无错。
4.3.4 扩展与现代应用
1. SEC-DED 码
标准的海明码只能纠正 1 位错误。如果发生 2 位错误,海明码可能会将其误判为另一位发生了 1 位错误,导致"越纠越错"。
为了解决这个问题,现代计算机内存(ECC RAM)通常使用 扩展海明码 。即在整个码字的最前面增加一个"全校验位" PglobalP_{global}Pglobal,用于校验所有位。这种方案被称为 SEC-DED (Single Error Correction, Double Error Detection),即:
- 纠正 1 位错误。
- 检测 2 位错误(但不能纠正)。
2. 实际应用领域
- 计算机内存 (ECC 内存):服务器通常使用带有海明编码功能的内存条。当内存中的电容因为宇宙射线等原因发生比特翻转时,硬件能自动纠正,防止服务器崩溃。
- RAID 2:虽然现代 RAID 系统更多使用异或校验(RAID 5)或更复杂的 Reed-Solomon 码(RAID 6),但 RAID 2 的原型设计就是基于海明码将数据分散在多个磁盘上。
- 卫星通信与深空探测:虽然现在已被 LDPC 码或 Turbo 码等更高效的编码取代,但在早期数字通信中,海明码因其编解码电路简单、延迟低,曾被广泛应用。
本章小结
海明距离揭示了冗余与纠错能力的数学关系,而海明码则通过巧妙的校验位布局,将数学理论转化为工程实践。理解海明码不仅有助于掌握计算机网络的底层逻辑,也是深入学习信息论与编码理论的必经之路。