一,数字滤波器
滤波器 是一种用来减少或消除干扰 的器件,其功能是对输入信号 进行过滤处理 得到所需的信号 。滤波器最常见的用法是对特定频率的频点或该频点以外的频率信号 进行有效滤除 ,从而实现消除干扰、获取某特定频率信号的功能。一种更广泛的定义是将具有能力进行信号处理的装置都称为滤波器。
滤波器的分类方法有很多种,从处理的信号形式来讲,可分为模拟滤波器和数字滤波器两大类。
- 模拟滤波器由电阻、电容、电感、运算放大器等组成,可对模拟信号进行滤波处理。
- 数字滤波器则通过软 件或数字信号处理器件对离散化的数字信号进行滤波处理。
随着数字信号处理理论的成熟、实现方法的不断改进,以及数字信号处理器件性能的不断提高,数字滤波器技术的应用也越来越广泛,已成为广大技术人员研究的热点。总体来说,与模拟滤波器相比,数字滤波器主要有以下特点:
- 数字滤波器是一个离散时间系统。应用数字滤波器处理模拟信号时,首先须对输入模拟信号进行限带、采样和A/D转换。数字滤波器输入信号的采样频率应大于被处理信号带宽的2倍,其频率响应具有 以采样频率为间隔的周期重复特性。为了得到模拟信号,数字滤波器 的输出数字信号需要经D/A转换和平滑处理。
- 数字滤波器的工作方式与模拟滤波器完全不同。模拟滤波器 完全依靠电阻、电容、晶体管等组成的物理网络实现滤波功能;数字滤波器则通过数字运算器件对输入的数字信号进行运算和处理。
- 数字滤波器具有比模拟滤波器更高的精度。数字滤波器甚至 能够实现模拟滤波器在理论上也无法达到的性能。例如,对于数字滤波器来说,可以很容易做到一个1000 Hz的低通滤波器,该滤波器允许999 Hz信号通过并且完全阻止1001 Hz的信号,模拟滤波器却无法区分 如此接近的信号。
- 数字滤波器比模拟滤波器有更高的信噪比。因为数字滤波器 是以数字器件执行运算的,从而避免了模拟电路中噪声信号(如电阻 热噪声)的影响。
- 数字滤波器具有模拟滤波器无法比拟的可靠性。组成模拟滤 波器部件的电路特性会随着时间、温度、电压的变化而漂移,而数字电路就没有这种问题。
- 数字滤波器的处理能力会受到系统采样频率的限制。根据奈奎斯特采样定理,数字滤波器的处理能力会受到系统采样频率的限制。如果输入信号的频率分量包含超过滤波器1/2倍采样频率的分量 时,数字滤波器就会因为频谱的混叠而不能正常工作。
- 数字滤波器与模拟滤波器的使用方式不同。
二,数字滤波器的分类
数字滤波器的种类很多,分类方法也不同,既可以从功能上分类,也可以从实现方法上分类,还可以从设计方法来分类。一种比较通用的分类方法是将数字滤波器分为两大类,即经典滤波器 和现代滤波器 。
经典滤波器 假定输入信号 x ( n )中的有效信号和噪声(或干扰)信号分布在不同的频带上,当 x ( n )通过一个线性滤波系统后,可以将噪声信号有效地减少或去除。如果有效信号和噪声信号的频带相互重叠,那么经典滤波器将无能为力。
经典滤波器主要有低通滤波器(Low Pass Filter,LPF) 、高通滤波器(High Pass Filter,HPF) 、带通 滤波器(Band Pass Filter,BPF) 、带阻滤波器(Band Stop Filter,BSF) 和**全通滤波器(All Pass Filter,APF)**等。
现代滤波理论研究的主要内容是从含有噪声信号的数据记录(又 称为时间序列)中估计出信号的某些特征或信号本身。一旦信号被估计出,那么估计出的信号将比原信号有更高的信噪比。
现代滤波器把有效信号和噪声信号都视为随机信号,利用它们的统计特征(如自相关函数、功率谱函数等)推导出一套最佳的估值算法,然后用硬件或软件实现。
现代滤波器 主要有维纳滤波器(Wiener Filter) 、卡尔曼滤波器(Kalman Filter) 、线性预测器(Liner Predictor) 、**自适应滤波器(Adaptive Filter)**等。一些专著将基于特征分解的频率估 计及奇异值分解算法也归入现代滤波器的范畴。
从实现的网络结构或者单位脉冲响应 来看,数字滤波器 可以分成无限脉冲响应(Infinite Impulse Response,IIR)滤波器 和有限脉 冲响应(Finite Impulse Response,FIR)滤波器,二者的根本区别在于两者的系统函数结构不同。
三,FIR滤波器
根据数字信号处理的基本理论,数字滤波器其实是一个时域离散系统,任何一个时域离散系统都可以用一个 N 阶差分方程来表示,即:
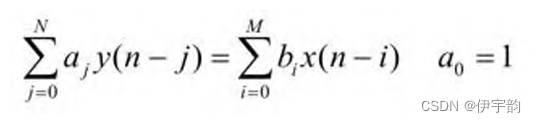
式中, x ( n )和 y ( n )分别是时域离散系统的输入序列 和输出序列 ; aj 和 bi 均为常数; y ( n - j )和 x ( n - i )项只有一次幂,没有相互交叉相乘项,故称为线性常系数差分方程 。差分方程的阶数是由方程中 y( n - j )项 j 的最大值与最小值之差确定的。 y ( n - j )项 j 的 最大值取 N ,最小值取0,因此称为N 阶差分方程。
一个时域离散系统的特征可以由单位脉冲响应 (也称为单位取样响应或单位采样响应) h ( n )完全表示, h ( n )是指输入为单位采样序列 δ ( n )时的输出响应。当滤波器(也是一个时域离散系统)的输入序列 为 x ( n )时,滤波器的输出 y ( n )可表示为输入序列 x ( n )与单位脉冲响应序列 h ( n )的线性卷积,即:

第一个式子中,当 aj =0且 j >0时,N 阶差分方程可表示为:
 式1-3
式1-3
对于上式,当输入序列为单位采样序列 δ ( n )时,得到的**单位脉冲响应 h ( n )**为:
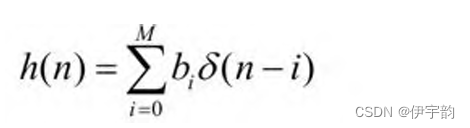
此时, h ( n )是长度为 M +1的有限长序列{ b (0), b (0),..., b ( M )},且 h (0)= b (0), h (1)= b (1),..., h ( M )= b ( M ),即 h ( n )就是由 bi (0< i ≤ M ) 组成的序列 。
我们把式(1-3) 表示的时域离散系统称为FIR滤波器 ,即有限脉冲响应滤波器 。顾名思义,是指单位脉冲响应的长度是有限的滤波器 。具体来讲,FIR滤波器的突出特点是其单位脉冲响应h(n)是一个 M +1点的有限长序列(0≤ n ≤ M )。其系统函数为:

从系统函数可以很容易看出,FIR滤波器只在原点上存在极点,这 使得FIR系统具有全局稳定性。
为了进一步了解FIR滤波器的输入/输出关系,以4阶FIR滤波器为例。根据式(1-3)可写出滤波器的输入/输出关系,即:
y ( n )= b0 x( n ) + b1 x( n-1)+ b2 x( n-2)+ b3 x( n-3)+ b4 x( n-4)由上式可以清楚地看出,FIR滤波器是由一个抽头延时线加法器 和乘法器 构成的,每一个乘法器的操作系数 就是一个FIR滤波器系数。因此,FIR滤波器的这种结构也称为抽头延时线结构。
FIR滤波器的FPGA设计需要完成两个基本步骤:
- 根据系统需求,采用MATLAB设计出符合频率响应特性的FIR 滤波器系数。
- 根据滤波器系数,采用FPGA实现对应的电路。
四,FIR滤波器的FPGA实现结构
一般来讲,FIR滤波器的基本结构可分为直接型 、级联型 、频率采、样型 、快速卷积型 、分布式等结构。其中直接型结构是FIR滤波器最常用的结构。
(1)基于累加器的FIR滤波器的FPGA设计
以4阶FIR滤波器为例,采用MATLAB仿真分析基于累加器的FIR滤波器性能,采用FPGA实现FIR滤波器。
根据前面的分析可知,数字滤波器主要用于分离频率信号 ,使某些频率的信号无损地通过 ,同时阻止某些频率的信号。
FIR滤波器 是指单位脉冲响应长度有限 的数字滤波器 。根据前文的分析可知,FIR滤波器的基本组成部分包括乘法器 、加法器 、单位延时 等。对于FPGA 来讲,加法器可以采用Verilog HDL中的加法运算实现, 乘法器可以采用乘法器IP核来实现,单位延时可以采用D触发器来实现 。在讨论复杂的FIR滤波器设计之前,先讨论一下简单的FIR滤波器设计,即基于累加器的FIR滤波器设计。
以4阶(长度为5)FIR滤波器为例,当FIR滤波器 的所有系数均为1时,滤波器的输出与输入关系为:
y(n)= x(n) + x(n-1) + x(n-2) + x(n-3) + x(n-4)此时的单位脉冲响应 h ( n )={1,1,1,1,1}。从上式可以看 出,FIR滤波器的表达式非常简单,其物理意义也很明确,即对连续输入的4个数据进行累加运算,得到FIR滤波器的输出结果。这种简单的FIR滤波器是如何对信号进行滤波处理的呢 ?我们先以一个具体的输入信号为例来进行说明。
假设输入的信号是由两个频率( f1=20 Hz, f2=2Hz)信号叠加形成的信号,即:

现以频率 fs=100 Hz对输入信号进行采样,即每间隔0.01 s采样一个数 据,可得到输入序列:

先通过MATLAB来仿真测试一下 。
matlab代码:
f1 = 20;
f2 = 2;
fs = 100;
t = 0 : 1/fs : 5;
s = sin(2*pi*f1*t) + sin(2*pi*f2*t);
b = [1,1,1,1,1];
y = filter(b,1,s);
figure(1);
subplot(211);plot(t,s);
legend('输入信号波形')
xlabel('时间/s');
ylabel('幅度/V');
subplot(212);plot(t,y);
legend('输出信号波形')
xlabel('时间/s');
ylabel('幅度/V');
figure(2);
freqz(b,1);MATLAB仿真得到的输入/输出信号波形如图所示 :

从上图所示的输入/输出信号波形 可以看出,输入信号是两个频率信号的叠加信号 ,输出信号是频率为2Hz的单频信号 。也就是说, 基于累加器的FIR滤波器将频率为20 Hz的信号完全滤除了,只剩下频 率为2 Hz的信号。
为什么会得到这样的结果呢?为什么长度为5(阶数为4)的FIR滤 皮器(由于FIR滤波器系数全部为1,因此相当于一个累加器)会将频 率为20 Hz的信号完全滤除,而完全保留频率为2 Hz的信号呢?
首先,从时域 来理解前面程序的运行结果。对于上式所示 的累加器,从时域 来看,输出序列等于连续5个输入数据之和 。对于输入信号中频率为20 Hz的信号,采样频率为100 Hz,每个周期正好有5 个采样数据 。对于正弦波信号来讲,每个周期采样的5个数据之和进行累加,刚好为0 。因此,长度为5的基于累加器的FIR滤波器,当采样频 率为100 Hz时,刚好可以完全滤除频率为20 Hz的信号 。同时,对于频 率为2 Hz的信号来讲,每个周期采样50个数据,对50个连续数据进行累加相当于在一定程度上的平滑处理,没有明显的滤除效果。
然后,从频域 来理解程序的运行结果。图中右面的表示相频响应,从中可以看出,系统的相频响应分段呈现线性 ,分别在0~ 0.4 、0.4~0.8 、0.8~1 内呈现线性 。其中横坐标为相对于π的归一化频率 。数字角频率与模拟频率有固定的转换关 系,如果系统的采样频率为fs ,则π对应于采样频率的一半,即fs/2 。在这, fs=100 Hz,因此0.4对应的模拟频率为 0.4× fs/2=20 Hz。
上图右面上面的图中上方的图表示幅频响应 ,图中的横坐标为相对于π的归 一化频率。纵坐标为幅度,单位为dB,计算公式为: G =20 ×lg A
式中, A 为放大倍数;G 为对放大倍数平方转换成以dB为单位的值 。当归一化频率为0.4(对应的模拟频率为20 Hz )时,对应的增益约为-45 dB ,进行了大幅度的衰减 ;当归一化频率为0.04(对应的模拟频率为2 Hz) 时,对应的增益约为14 dB ,提高为原来的5倍 。从上图左面图中可以看出,滤波后的2 Hz信号的幅度为5 V ,刚好是输入信号幅度(1 V)的5 倍
所以采用MATLAB中的函数 可以直接实现滤波运算 ,但在FPGA 中则需要用加法器、乘法器、触发器 等来搭建FIR滤波器电路,从而实现对输入信号的滤波处理。对于基于累加器的FIR滤波器的FPGA实现来讲,需要在FPGA中实现上式所示的运算。如前所述,在FPGA中 实现FIR滤波器可以采用直接型、级联型等不同的结构,由于直接型结构简单高效,采用直接型,如下图:

Verilog 代码如下:
module FIR(
input clk ,
input signed [8:0] xin ,
output signed [11:0] yout
);
//产生4级出发触发输出信号,相当于4级延时
reg signed [8:0] x1,x2,x3,x4;
always @(posedge clk) begin
x1 <= xin;
x2 <= x1;
x3 <= x2;
x4 <= x3;
end
//对5个连续的输入信号累加
assign yout = xin + x1 + x2 + x3 + x4;
endmodule需要注意的是,由于输入数据 和输出数据 均为有符号数 ,因此程序中的所有数据均定义为signed类型的数据。
(2)采用并行结构设计15阶FIR滤波器
所谓并行结构 ,即并行实现滤波器的累加运算 。具体来讲,就是先并行地将具有对称系数的输入数据相加,再采用多个乘法器并行实 现系数与数据的乘法运算 ,最后将所有乘积结果相加后输出。
根据FPGA设计原理以及并行结构的特点,对于15阶的FIR滤波器的运算,可采用以下步骤实现。
- 设计移位寄存器实现输入数据的15级移位输出。
- 采用8个加法器完成对称输入数据的加法运算。
- 采用8个乘法器并行完成输入数据与FIR滤波器系数的乘法运 算。
- 完成8输入加法器运算,输出FIR滤波器的结果。
代码如下:
module FIR_parallel(
input clk,
input signed [7 : 0] Xin,
output signed [21: 0] Yout
);
//数据存入到移位寄存器
reg signed [7:0]Xin_reg [15:0];
always @(posedge clk ) begin
Xin_reg[0 ] <= Xin;
Xin_reg[1 ] <= Xin_reg[0 ];
Xin_reg[2 ] <= Xin_reg[1 ];
Xin_reg[3 ] <= Xin_reg[2 ];
Xin_reg[4 ] <= Xin_reg[3 ];
Xin_reg[5 ] <= Xin_reg[4 ];
Xin_reg[6 ] <= Xin_reg[5 ];
Xin_reg[7 ] <= Xin_reg[6 ];
Xin_reg[8 ] <= Xin_reg[7 ];
Xin_reg[9 ] <= Xin_reg[8 ];
Xin_reg[10] <= Xin_reg[9 ];
Xin_reg[11] <= Xin_reg[10];
Xin_reg[12] <= Xin_reg[11];
Xin_reg[13] <= Xin_reg[12];
Xin_reg[14] <= Xin_reg[13];
Xin_reg[15] <= Xin_reg[14];
end
//采用加法器 实现对称系数相加
reg signed [8:0]Xin_add[7:0];
always @(posedge clk ) begin
Xin_add [0] <= Xin_reg[0] + Xin_reg[15];
Xin_add [1] <= Xin_reg[1] + Xin_reg[14];
Xin_add [2] <= Xin_reg[2] + Xin_reg[13];
Xin_add [3] <= Xin_reg[3] + Xin_reg[12];
Xin_add [4] <= Xin_reg[4] + Xin_reg[11];
Xin_add [5] <= Xin_reg[5] + Xin_reg[10];
Xin_add [6] <= Xin_reg[6] + Xin_reg[9 ];
Xin_add [7] <= Xin_reg[7] + Xin_reg[8 ];
end
//例化乘法ip核
wire signed [20:0] xout[7:0];
mult u0(.clk(clk), .a(Xin_add[0]) .b(12'd0 ) .p(xout[0]));
mult u1(.clk(clk), .a(Xin_add[1]) .b(12'd7 ) .p(xout[1]));
mult u2(.clk(clk), .a(Xin_add[2]) .b(12'd15 ) .p(xout[2]));
mult u3(.clk(clk), .a(Xin_add[3]) .b(12'd46 ) .p(xout[3]));
mult u4(.clk(clk), .a(Xin_add[4]) .b(12'd307 ) .p(xout[4]));
mult u5(.clk(clk), .a(Xin_add[5]) .b(12'd850 ) .p(xout[5]));
mult u6(.clk(clk), .a(Xin_add[6]) .b(12'd1545 ) .p(xout[6]));
mult u7(.clk(clk), .a(Xin_add[7]) .b(12'd2047 ) .p(xout[7]));
//2级流水线实现加法
reg signed [20:0]sum1,sum2;
always @(posedge clk) begin
sum1 <= xout[0] + xout[1] + xout[2] + xout[3] ;
sum2 <= xout[4] + xout[5] + xout[6] + xout[7] ;
Yout <= sum1 + sum2;
end
endmodule参考文献:
1\]褚振勇,屈丹,门向生.利用FPGA实现数字信号处理\[J\].电讯技术,2006,(1):91-96 \[2\]杜勇.Xilinx FPGA 数字信号处理设计\[M\].电子工业出版社:202003.339. \[3\]王媛,金磊,曾富华.基于FPGA的多功能FIR数字滤波器设计\[J\].现代电子技术,2023,46(18):38-42.DOI:10.16652/j.issn.1004-373x.2023.18.007. \[4\]刘虹雨.基于FPGA的FIR滤波器电路设计研究\[D\].电子科技大学,2023.DOI:10.27005/d.cnki.gdzku.2023.003142. \[5\]张海军.基于FPGA的16阶FIR滤波器的设计与实现\[J\].安徽大学学报(自然科学版),2009,33(01):62-65+69.